基于半经典近似研究费米气体的稳定性及顺磁性
田青松, 门福殿, 陈新龙
(中国石油大学(华东)理学院, 青岛 266580)
基于半经典近似研究费米气体的稳定性及顺磁性
田青松, 门福殿, 陈新龙
(中国石油大学(华东)理学院, 青岛 266580)
基于半经典近似方法, 给出重力场和强磁场共存下费米子的能谱. 然后由泊松公式导出费米气体的热力学势函数. 在此基础上, 运用热力学关系式求解低温条件下系统的稳定性及磁化率的解析式, 并通过数值模拟分析强磁场背景下重力场对稳定性及顺磁性的影响机制.
重力场; 强磁场; 费米气体; 稳定性; 顺磁性
1 引 言
近年来, 研究外势及相互作用同时对量子系统热力学性质的影响已成为热点. 特别是对谐振势约束下的量子系统的研究, 取得了一系列成果[1-9]. 另外, 对费米系统的研究也逐渐增加. 如文献[10]研究了强磁场中费米气体的稳定性及顺磁性; 文献[11]研究了强磁场中费米气体的统计性质; 文献[12]研究了强磁场中超冷费米气体的相对论效应. 文献[13]研究了强磁场中相互作用费米气体的相对论稳定性. 但在强磁场背景下, 重力场对费米系统的稳定性及顺磁性尚无人涉及. 重力场是一种常见而又重要的势场, 在强磁场背景下, 研究重力场对费米系统的稳定性及顺磁性的影响, 尤其是对于有精细结构的费米系统如6Li原子系统, 具有重要的理论价值和实际意义. 本文基于半经典近似方法, 通过泊松公式解析双场共存下费米系统的低温热力学势函数, 在此基础上运用热力学关系和数值模拟方法分析强磁场背景下重力场对系统稳定性、 磁化率的影响机制.
2 同时考虑重力场和强磁场情况下的热力学势函数
z.
(1)
式中σ=he/4πmc为玻尔磁子,n=0,1,2,3…为量子数.mgz为重力场作用项. 根据文献[15], 当n,pz给定时, 在Δpz区间内的态数为
(2)
其中Lz为粒子在z方向的运动区域的尺度, 令Lz=Δz, 即粒子z方向的运动尺度在有限范围内为一可变的量. 再考虑自旋, 则粒子在ΔpzΔz区间的态数为
(3)
再根据文献[14],pz是在磁场方向的动量, 取-∞到∞的连续值,z取0到z的有限连续值, 对于每个给定的n在间隔dpzdz中的态的数目是
(4)
则系统的热力学函数可表示为
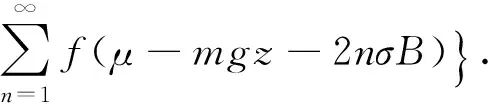
(5)
其中
(6)
利用泊松公式
(7)
(5)式可表为
(8)
其中Ω0(μ)为无外场时系统的热力学势函数. 系统的热力学势函数可表为
Ω=Ω0(μ)+ΩB+G(μ),
(9)
其中ΩB+G(μ)为含有磁场和重力场的影响项. 经计算, 得
(10)
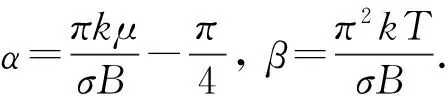
3 系统的稳定性条件及磁化率
令Sz=V, 则(10)式可化为
(11)
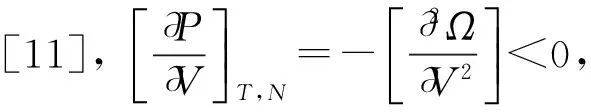
(12)
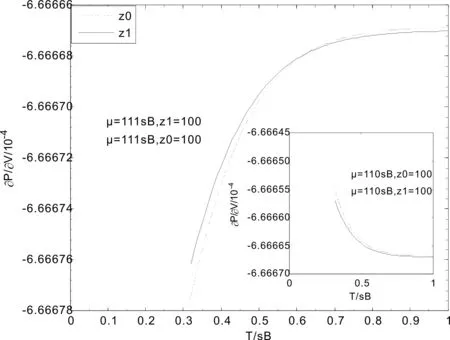
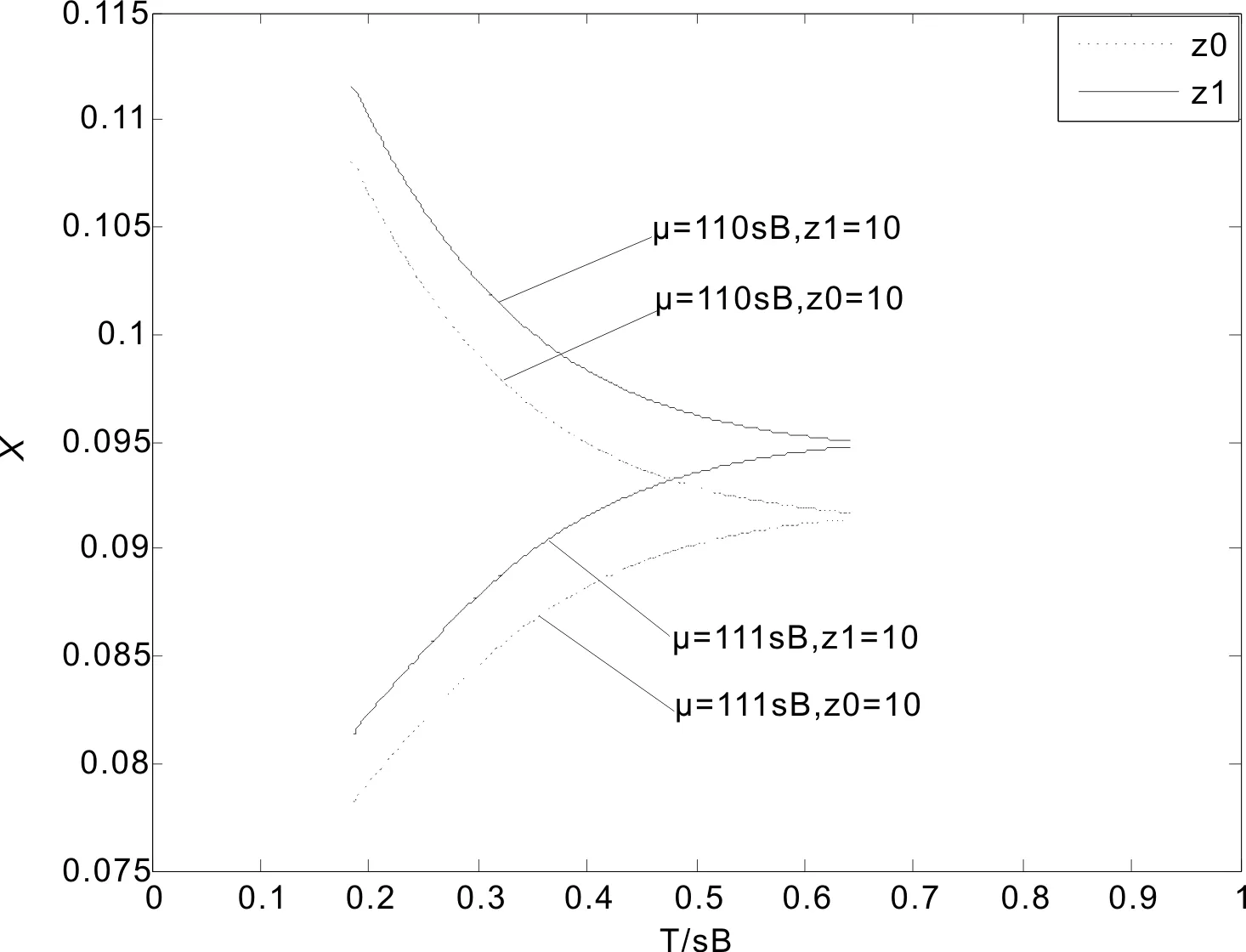
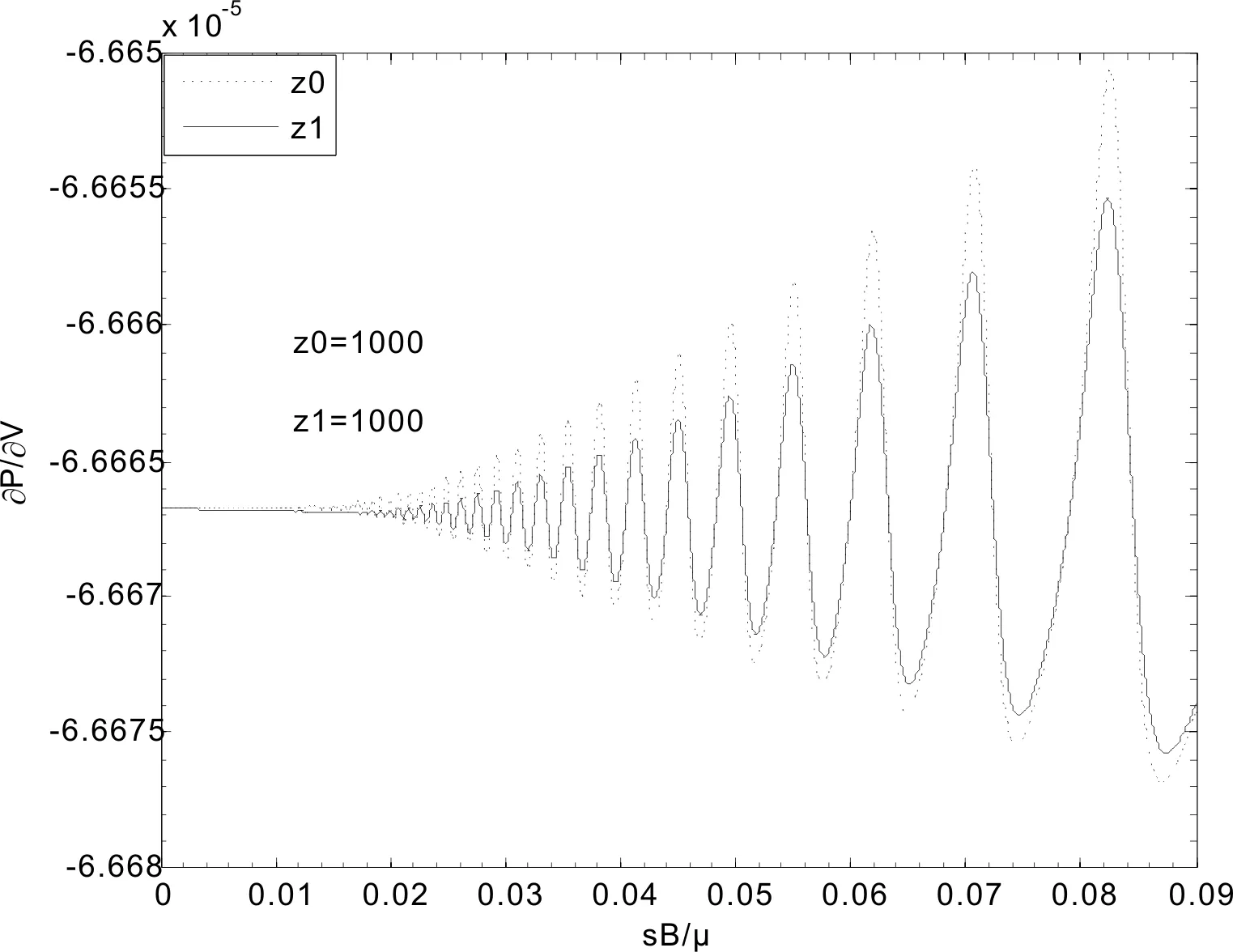
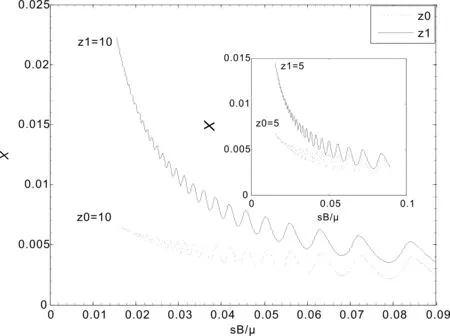
考虑强磁场条件T≤σB≤μ, 令μ=xσB,T=yσB(即x≥1, 0 (13) (14) (16) 图1 稳定性随温度的变化Fig. 1 The stability varies with temperature 图2 磁化率随温度的变化Fig. 2 The susceptibility varies with temperature 图3 稳定性随磁场的变化Fig. 3 The stability varies with magnetic field 图4 磁化率随磁场的变化Fig. 4 The susceptibility varies with magnetic field 在以上图中z0是表示有磁场无重力场时的情况, z1是磁场和重力场共存下的情况, z0和z1的值都是公式中z的取值. 图1显示, 当μ为偶数(如μ=110σB)时, 与单纯强磁场相比, 重力场的加入使稳定性加强, 即重力场强化了系统的稳定性, 但这种影响随温度的升高在减弱; 当μ为奇数(如μ=111σB)时, 与单纯强磁场相比, 重力场的加入使稳定性随温度的变化存在着一转折温度T0, 当温度低于T0时, 重力场使系统的稳定性降低, 当温度高于T0时, 重力场使系统的稳定性加强. 从图2可看出, 无论μ为偶数还是奇数, 与单纯强磁场相比, 重力场的加入都使磁化率有所增加, 这种增加随温度的增加略有放大, 且磁化率随温度变化的特征不因重力场的加入而改变. 图3表明, 单纯强磁场下, 稳定性随磁场的增加出现规则振荡, 振幅逐渐增加, 振荡中心为一水平直线; 加入重力场后, 与单纯强磁场相比, 振荡中心稍微上移, 振幅增大, 相位几乎不变. 图4显示, 单纯强磁场下, 磁化率随磁场的增加振荡中心逐渐降低, 振幅逐渐增加; 与单纯强磁场情况相比, 重力场的加入使磁化率增加, 但随磁场的加强这种影响逐渐减弱. 当高度减小时, 重力场对磁化率的影响也降低. 本文基于强磁场条件, 根据半经典近似的方法引入重力场, 然后用理论解析和数值模拟的方法研究了重力场和强磁场共存条件下费米气体的稳定性及顺磁性, 分析了强磁场背景下重力场对费米气体的稳定性及顺磁性的影响. 研究表明, 从稳定性随温度的变化来看, 与单纯强磁场相比, 当μ为偶数时, 重力场强化系统稳定性; μ为奇数时, 重力场的加入使稳定性随温度的变化存在着一转折温度T0, 当温度低于T0时, 重力场使系统的稳定性降低, 当温度高于T0时, 重力场使系统的稳定性加强. 从磁化率随温度的变化来看, 无论μ为偶数还是奇数, 重力场的加入都使磁化率有所增加. 从稳定性随磁场的变化看, 加入重力场后, 振荡中心稍微上移, 振幅增大, 相位几乎不变. 从磁化率随磁场的变化看, 重力场的加入使磁化率减小, 但随磁场的加强这种影响逐渐减弱. [1]LiMZ,YanJZ,ChenJC, et al.ThermodynamicpropertiesofanideaFermigasinanexternalpotentialwithinanydimensionalspace[J]. Phys. Rev.A, 1998, 58(2): 1445. [2]LiMZ,LinHS,ChenLX, et al.ChemicalpotentialandheatcapacityofanidealFermigastrappedinaharmonicpotentialinanydimensionalspace[J]. Journal of Xiamen University (Natural Science), 1998, 37(4): 498 (inChinese) [李明哲, 林海生, 陈丽璇, 等.n维空间简谐势阱中理想费米气体的化学势与热容量[J]. 厦门大学学报(自然科学版), 1998, 37(4): 498] [3]NoronhaJMB,TomsDJ.ThespecificheatofatrappedFermigas:ananalyticalapproach[J]. Phys. Lett.A, 2000, 267(4): 276. [4]ButtsDA,RokhsarDS.TrappedFermigas[J]. Phys. Rev.A, 1997, 55(6): 4346. [5]BruunGM,BurnettK.InteractingFermigasinaharmonictrap[J]. Phys. Rev.A, 1998, 58(3): 2427. [6]OlivaJ.DensityprofileoftheweaklyinteractingFermigasconfinedinapotentialwell:Nonzerotemperature[J]. Phys. Rev.B, 1989, 39(7): 4204. [7]RothR,FeldmeieH.Effectives-andp-wavecontactinteractionsintrappeddegenerateFermigases[J]. Phys. Rev.A, 2001, 64(4): 043603. [8]SuGZ,ChenLX.ThermodynamicpropertiesofaweaklyinteractingFermigas[J]. Acta. Phys. Sin., 2004, 53(4): 984 (inChinese) [苏国珍, 陈丽璇. 弱相互作用费米气体的热力学性质[J]. 物理学报, 2004, 53(4): 984] [9]SuGZ,ChenJC,ChenLX.Low-temperaturebehaviorofaweaklyinteractingFermitrappedinapower-lawpotential[J]. Phys. Lett.A, 2003, 315(1-2): 109. [10]MenFD,WangHT,HeXG.ThestabilityandparamagnetismofFermigasinastrongmagneticfield[J]. Acta. Phys. Sin., 2012, 61(10): 100503 (inChinese) [门福殿, 王海堂, 何晓刚. 强磁场中Fermi气体的稳定性及顺磁性[J]. 物理学报, 2012, 61(10): 100503] [11]MenFD,FanZL.StatisticpropertiesofFermigasinastrongmagneticfield[J]. Chin. Phys.B, 2010, 19(3): 030502. [12]MenFD,HeXG,ZhouY, et al.RelativisticeffectofultracoldFermigasinastrongmagneticfield[J]. Acta. Phys. Sin., 2011, 60(10): 100502 (inChinese) [门福殿, 何晓刚, 周勇, 等. 强磁场中超冷费米气体的相对论效应[J]. 物理学报, 2011, 60(10): 100502] [13]WangLL,MenFD,ZhangYP, et al.RelativisticstabilityofinteractingFermigasinastrongmagneticfield[J]. J. At. Mol. Phys., 2013, 30(4): 607 (inChinese) [王丽林, 门福殿, 张一鹏, 等. 强磁场中相互作用费米气体的相对论稳定性[J]. 原子与分子物理学报, 2013, 30(4): 607] [14]LandauLD,LifshitzEM. Statistical physics partI[M]. 3rded.Oxford:PergamonPress, 1999. [15]LandauLD,LifshitzEM. Quantum mechanics (Non-relativistic Theory) [M]. 3rded.Oxford:PergamonPress, 1999. Study of the stability and paramagnetism of Fermi gas based on the semiclassical approximation TIAN Qing-Song, MEN Fu-Dian, CHEN Xin-Long (College of Science, China University of Petroleum(East China), Qingdao 266580, China) Based on the semiclassical approximation, the energy spectrum of single fermion trapped in both gravitational field and strong magnetic field is given. By using Poisson’s formula, the thermodynamic potential function of Fermi gas is derived. Furthermore, by using the thermodynamic relationships, the analytical expressions of the stability and magnetic susptibility of the system at low temperature are obtained. The influence mechanism of gravitational field on the thermodynamic properties of the system in the background of strong magnetic field is analysed by numerical simulation. Gravitational field; Strong magnetic field; Fermi gas; Stability; Paramagnetism 103969/j.issn.1000-0364.2015.12.025 2014-09-24 田青松(1988—),男, 河南商丘人, 硕士研究生, 主要研究方向为量子统计.E-mail: tqs728@126.com 门福殿. E-mail: menfudian@163.com O414.1; O414.2 A 1000-0364(2015)06-1059-05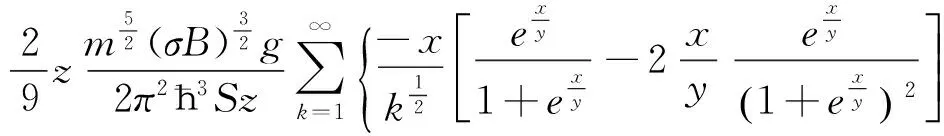

4 数值模拟与分析
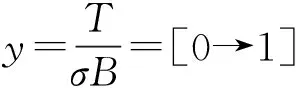
5 结 论

