建筑结构动力特性简化与抗震性能有限元分析

王长虹

(上海应用技术学院轨道交通学院，上海200235)

1 引言

在建筑结构动力学计算中，为了节约运算时间和减少建模的工作量，经常需要建立简化的结构动力学分析有限元模型。在动力学分析计算中，建筑结构抽象为多质点模型，将建筑结构的刚度简化为梁的刚度，建筑结构的质量按集中质点处理。通常情况下，建筑结构各质点实际的质心、形心和剪心不在同一几何位置，导致计算结果不能真实地反映原结构的力学状态［1］。另外，简化建筑结构模型的结果精度不仅限于刚度和质点几何位置，而且还涉及阻尼的影响，动力学计算中，以Rayleigh阻尼最为常用，将系统假设为比例阻尼来处理，阻尼的建模对少数振型参与计算时精度较好，当取大量振型参与计算时，精度有可能失控［2］。

为了分析简化建筑结构模型的质点几何位置以及阻尼特性对计算结果精度的影响，通过Ansys软件中Beam44单元和Matrix27单元的介绍，建立考虑建筑结构的质心、形心和剪心变化的简化三维模型和真三维模型;并根据材料模态阻尼比、质量矩阵、振型矩阵直接计算阻尼矩阵，通过数值分析对比建筑结构动力特性与时程计算结果，全面了解简化建筑结构模型动力特性与抗震性能的计算效率和结果精度的影响因素。

2 ANSYS单元介绍

2．1 Beam44 单元

Beam44梁单元可用于拉伸、压缩、扭转、弯曲计算，单元有两个节点I和J，每个节点有6个自由度、3个平动自由度和3个转动自由度，两个节点可以是不同的非对称几何截面，并根据中心线扫略成不规则梁单元。

梁单元横截面参数可以通过实常数描述，如转动惯量、截面尺寸、剪心和质心偏移值等，Jzz和Jyy是围绕截面形心主轴的转动惯量，当不指定扭转转动惯量Jxx时，值为Jzz与Jyy之和。转动惯量在J端截面没有特别指定时，将和I端截面采用同样数值。

梁单元I端截面质心偏移值 Dx1、Dy1、Dz1，和剪心偏移值DSCY1、DSCZ1的正负号规定与单元坐标系指向一致，TKYT1、TKYB1定义了截面Y方向的尺寸，TKZT1、TKZB1定义了截面Z方向的尺寸，当不特别指定梁单元J端截面参数时，将复制I端截面的参数。梁单元截面见图1。

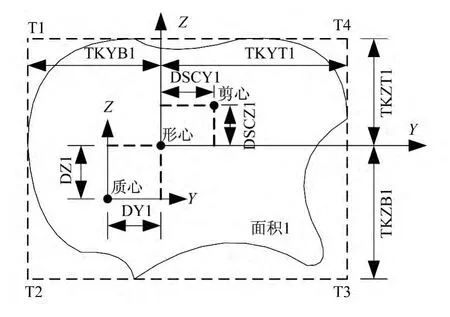
图1 梁单元截面Fig．1 Beam element section

2．2 Matrix27 单元

Matrix27可代表一种任意的单元，单元的几何特性无定义，但其弹性运动学响应可用刚度、阻尼或者质量系数来指定。单元连接2个节点，每个节点有6个自由度:沿节点坐标系X、Y、Z方向的平动和绕节点坐标系X、Y、Z方向的转动。

单元生成12×12维的矩阵。自由度排列的顺序为:I节点的X方向平动自由度(UX)、Y方向平动自由度(UY)、Z方向平动自由度(UZ)、绕X轴转动的自由度(ROTX)、绕Y轴转动的自由度(ROTY)、绕Z轴转动的自由度(ROTZ)，然后是J节点的如上6个自由度。如果有一个节点没有使用，则它在矩阵中对应的全部行和列默认为0。Matrix27单元描述见图2。

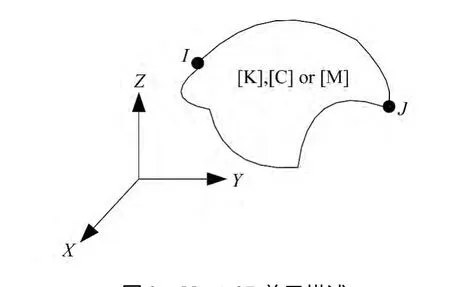
图2 Matrix27单元描述Fig．2 Description of element Matrix27

当定义为阻尼单元时，指定KEYOPT(3)=5，表示此单元定义的是12×12维的阻尼矩阵。

3 工程介绍

抗震规范［3］要求，对于复杂结构的抗震分析，应该采用不少于两个不同的力学模型，并对其计算结果进行分析比较。简化三维模型和真三维模型是两种不同性质的结构体系，采用这两种模型，可满足规范要求。

如图3所示，某核电站建筑物为二层框架结构，建筑面积为200 m2，高度为22．607 m，质量为15 567 t，对抗震性能要求极高。

真三维有限元建模采用Beam44单元模拟梁柱，Shell181单元模拟楼板，Mass21单元模拟集中质量，真三维模型共12 322个单元，7 452个节点。

简化三维模型由于质心、形心、剪心不重合，在计算过程中，质心和形心之间采用主从自由度耦合，形心、质心和剪心的几何位置由Beam44单元实常数设定。

图3 真三维模型图Fig．3 Real three dimensional model

如图4所示，根据建筑物的形状，质量分布和抗震性能计算得出各楼层质心、形心和剪心位置，如表1所示，建筑物的几何参数如表2所示，建筑物的材料参数如表3所示。

图4 简化三维模型Fig．4 Simplified three dimensional model

表1 质量参数Table 1 Mass parameters

表2 几何参数Table 2 Geometry parameters

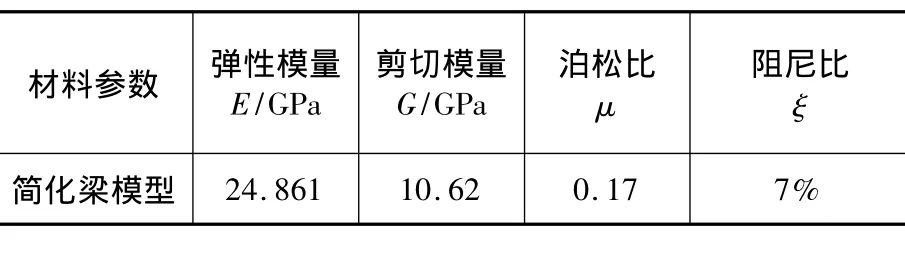
表3 材料参数Table 3 Material parameters

地震作用力来自于三个方向，南－北方向地震，即X轴方向;东－西方向地震，即Y轴方向;竖直方向地震，即Z轴方向。

简化三维模型取线弹性模型，考虑到建筑物采用筏板基础，刚度大，地基的嵌固作用也较强，所以视基础底面为完全嵌固。

4 结构动力特性分析

4．1 模态分析

在动力学计算中，阻尼作用通过Rayleigh阻尼矩阵确定，实现了任两阶(或少数阶)模态阻尼比的建模控制，公式如下所述:

式中，［C］为阻尼矩阵;［M］为质量矩阵;［K］为刚度矩阵;α，β为常数，可以根据任意两个模态阻尼比 ξi和 ξj决定:

ωi表示第i阶模态的圆频率。这种生成方法只在第i，j阶才严格保证模态阻尼比计算值为设定值，而其他阶的模态阻尼比则不能保证。

根据材料模态阻尼比、质量矩阵、振型矩阵直接计算阻尼矩阵的公式如下所示:

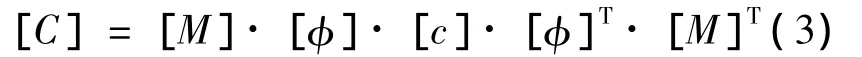
式中，［M］为m×m阶质量矩阵，m表示质点自由度;［Φ］为m×n阶无阻尼运动振型特征向量矩阵，n为基频提取阶数，由模态计算Block Lancos方法得到;ci，i=4πξi/ωi为 n × n 阶方阵主对角线元素，ξi取 0．07。

需要说明的是，式(3)仅适合于简化三维模型，而对于真三维模型，计算量巨大，分析依然采用Rayleigh阻尼矩阵。

如图5所示，得到阻尼矩阵以后，通过Matrix27单元输入系统。

图5 阻尼矩阵Fig．5 Damping matrix

采用QR Damped方法计算结构的基频和振型等动力特征。表4为简化三维模型无阻尼、简化三维模型自定义阻尼、真三维模型Rayleigh阻尼模态分析对比结果。

表4 结构基频对比Table 4 Comparison of structure natural frequency

表4的结果说明，简化三维模型通过设定质心、形心和剪心，考虑阻尼的影响，与真三维模型计算的基频结果基本一致，最大相差值为3．83%。图6、图7为真三维模型和简化模型的第一阶振型图。

图6 真三维模型第一阶振型Fig．6 First mode of real model

图7 简化三维模型第一阶振型Fig．7 First mode of simplified model

结构表现出有代表性的振型如图7所示，以水平侧移和扭转振型为主，竖向振型出现在高阶振型，但表现不明显。

4．2 振型参与系数分析

简化三维模型在各个方向上的振型参与系数如图8所示，可以得出X、Y方向上均是低阶振型起到控制作用，Z方向上由第6阶振型起控制作用。

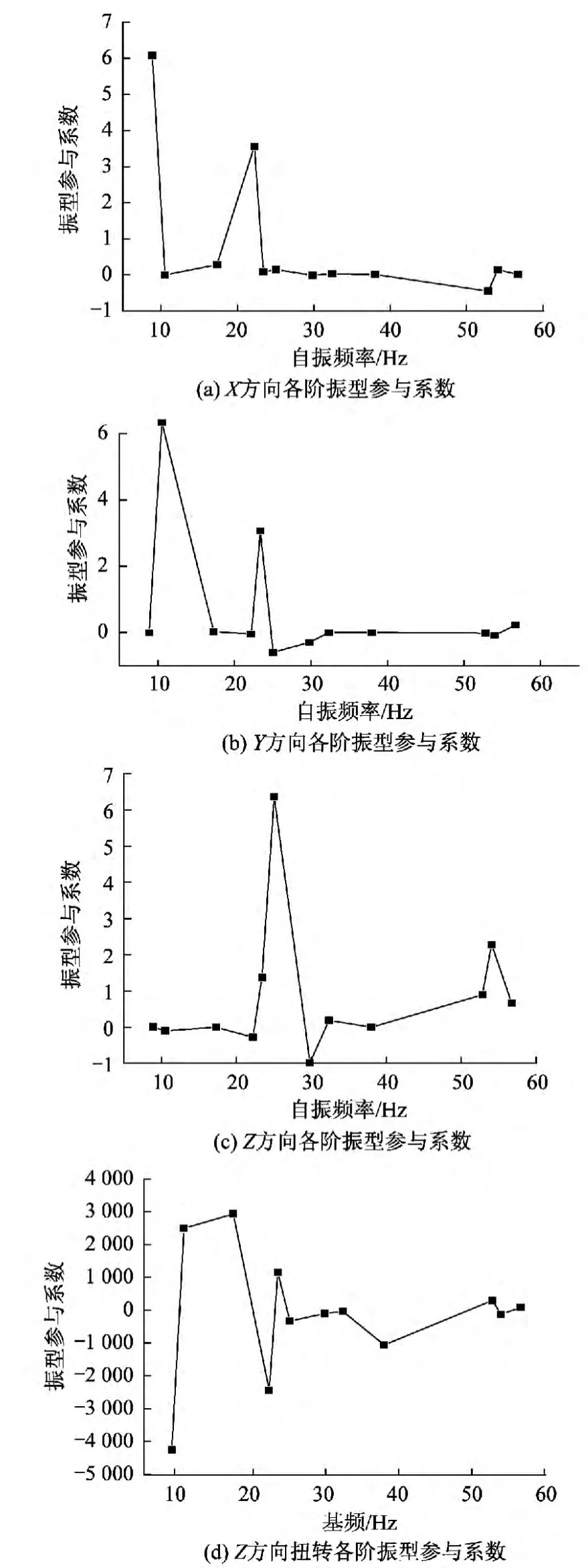
图8 各阶振型参与系数Fig．8 Participation coefficents of different vibration modes

4．3 振型数目的确定

振型个数一般取振型参与质量(有效质量)达到总质量的90%时所需要的振型数目［4］，这种方法称为有效质量法。图9的横坐标为基频，纵坐标为有效质量比(振型参与质量/总质量)，可以得到当参与质量达到90%的时候，需要的振型分别为4阶(X向)，5阶(Y向)，11阶(Z向)。同时，考虑到取过多振型对计算结果影响较小，却带来不必要的计算量，所以在用模态叠加法时程分析的时候，提取模态阶数在10～20阶比较合理。

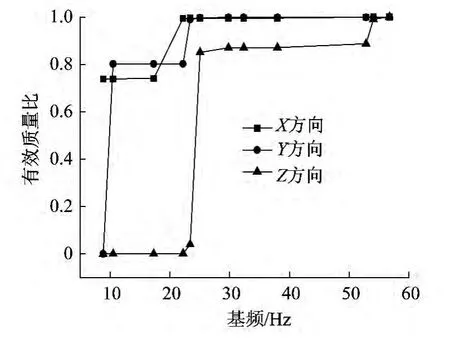
图9 各阶振型参与质量比重Fig．9 Mass fractions of different vibration modes

4．4 结构自振特性分析

(1)基频较高，第一基频为8．88 Hz，反映了结构整体刚度大的特点;

(2)结构以扭转为主的第一自振基频与平动为主的第一自振基频的比值为 0．51(8．88/17．31)，扭转效应对结构的影响不明显，抗扭能力满足要求;

(3)水平振型为主，竖向振型表现不明显;

(4)考虑到竖向振型对结构响应的影响，真三维模态叠加时程分析方法应该考虑20阶以上的振型;

(5)从结构振型可以得出，建筑结构如果考虑质心、形心、剪心的几何分布，并加入合适的阻尼效应，采用简化三维模型能够得到合理的结果，且高效可靠。

5 地震响应分析

地震响应分析主要采用时程分析方法，对比分析简化三维模型和真三维模型在地震作用下的响应。地震波X、Y、Z向均不同，每次仅考虑单方向的地震波影响，地震作用取当地实测地震波，时间为22．09s，如图10 所示。

5．1 简化三维模型分析

简化三维模型采用ANSYS软件的瞬态结构分析技术，根据计算速度和对计算机硬件的需求，迭代求解方式为PCG方式［5］。采用Newmark积分方式，δ=0．5，α ＞ 0．25 时无条件稳定，且具有较高精度，这里采用控制振幅衰减的方法，取γ=0．005为积分参数，采用的 CPU为奔腾四代2．3G，内存1G的 PC电脑进行计算，一条4 418个数据的地震波的时程分析需要时间约20分钟，效率极高。

X方向地震波得到的基底最大剪力为68．034 kN，Y方向地震波得到的基底最大剪力为67．953 kN，与建筑结构总重量相比，剪重比较小。采用时程分析方法得到的结果中，建筑结构顶部在单向地震作用下的响应如表5所示。

弹性时程分析时，在不同方向的地震波作用下，质点水平位移的包络图响应曲线见图11，质点的加速度放大系数如图12所示，观察一层、二层顶板质点在X和Y方向的地震波作用下，结构的水平位移随时间的变化曲线。

5．2 真三维模型分析

真三维模型由于单元较多，没有采用完全法计算时程响应，而是采用模态叠加法，基频取前20阶，一条地震波需要的计算时间为2小时，基本在可以承受的时间范围内。结构顶层的水平位移随时间的变化曲线如图13所示。

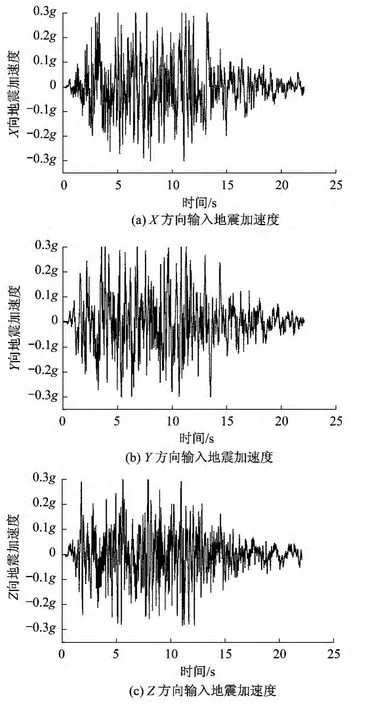
图10 地震波Fig．10 Seismic wave

表5 顶层最大响应及发生时刻Table 5 Maximum reaction of the top storey and its time

对比表5与图13的结果，X方向地震水平位移简化三维模型和真三维模型的计算结果相差20%;Y方向地震水平位移简化三维模型和真三维模型的计算结果相差1%。

5．3 对比分析结果

由时程分析的对比结果，可以得到如下结论:

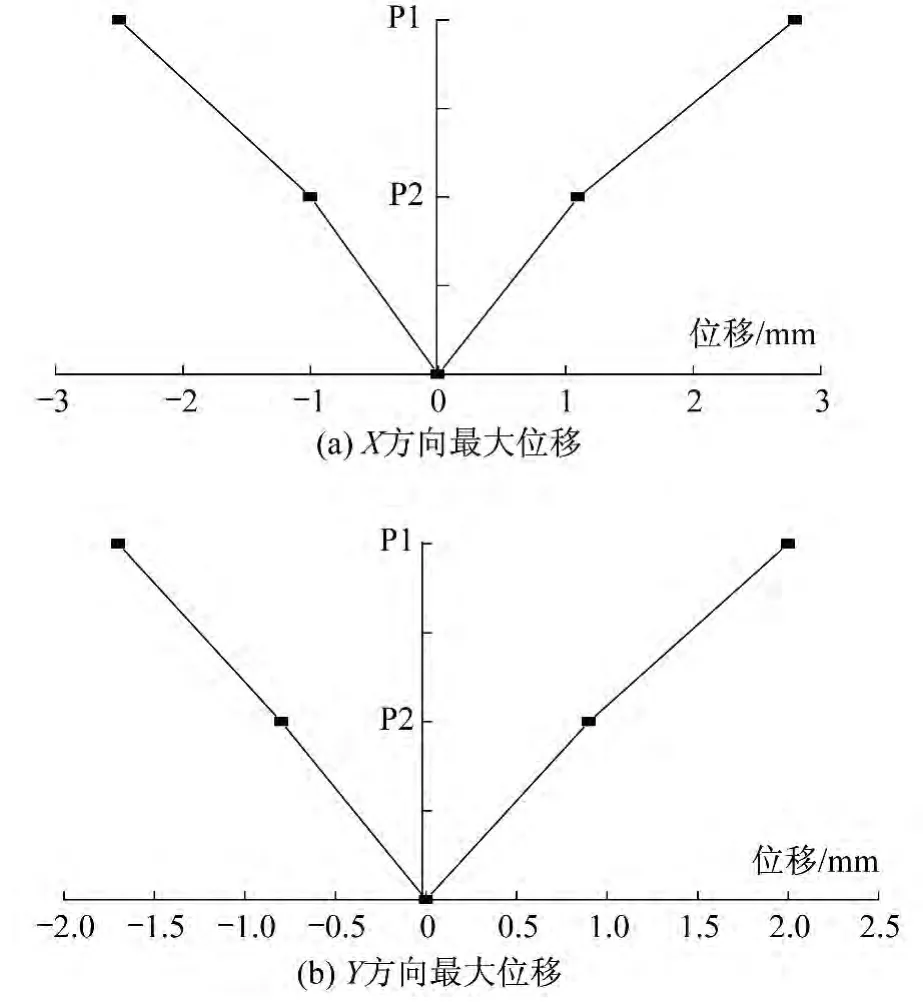
图11 楼层水平位移包络图Fig．11 Horizontal displacement envelope diagram of each storey

图12 楼层水平加速度放大系数曲线Fig．12 Acceleration amplification coefficient curve of each storey

(1)结构的时程分析可以得到结构随着时间变化的楼层位移曲线。结构在单向地震波作用下的表现反映出地震波的随机性，统计规律表明X方向的侧向位移要大于Y方向的侧向位移。

(2)从图11至图13可以得出，该建筑受地震的整体作用影响较小，只是在二层顶板的位置，结构的加速度和位移达到峰值，是结构的薄弱环节，该位置需要采取构造措施进行特别处理。

(3)所采用的加速度时程曲线，其加速度峰值相同，但每条地震波均有其特性的频谱，按不同波形计算出的结构地震反应，结果较为可靠。

(4)时程计算中，简化三维模型与真三维模型的计算结果接近，差值在20%以内，表明简化三维模型具有计算速度快、计算精度高的特点。

图13 地震波作用下时程分析结果Fig．13 Result of time-history analysis in earthquake

6 结论

通过有限元软件ANSYS建立建筑结构的简化三维模型和真三维模型，对该结构的动力计算和比较，可以得到结论如下:

(1)简化三维模型考虑建筑结构的质心、形心和剪心几何分布后，计算模型可以正确反映复杂结构的动力特征。

(2)Rayleigh阻尼适合于少数阶振型起控制作用的情况，由于简化三维模型的动力特征受阻尼的影响比较大，必须要综合考虑质量、振型和模态阻尼比的影响。

(3)有限元软件ANSYS可以考虑质点系质心、形心和剪心不统一的情况，并可自定义阻尼矩阵，为复杂建筑结构的动力学分析提供了高效、可靠的计算平台。

建筑结构在动力特征和抗震性能分析中，采用简化模型和真三维模型都是可行的，主要是根据客观需求合理建立模型。

致谢:本文在撰写过程中，得到日本大林组亚洲博士的指导，在此表示衷心的感谢。

［1］ Clough C W，Penizen J．Dynamics of structures［M］．2th Edition．New York:McGram-Hill Inc．，1993．

［2］ 淡丹辉，孙利民．结构动力有限元的模态阻尼比单元阻尼建模法［J］．振动、测试与诊断，2008，28(2):100-103．Dan Danhui，Sun Limin．Damping modeling and its evaluation based on dynamical analysis of engineering structure by finite element method［J］．Journal of Vibration，Measurement and Diagnosis，2008，28(2):100-103．(in Chinese)

［3］ 中华人民共和国建设部．GB 50011—2001建筑抗震设计规范［S］．北京:中国建筑工业出版社，2002．Ministry of Construction of the People's Republic of China GB 50011—2001 Code for seismic design of buildings［S］．Beijing:China Architecture and Building Press，2002．(in Chinese)

［4］ 王元清，黄怡，石永久，等．超高层钢结构建筑动力特性与抗震性能的有限元分析［J］．土木工程学报，2006，39(5):65-71．Wang Yuanqing，Huang Yi，Shi Yongjiu，et al．Finite element analysis on dynamic characteristics and seismic resistance of super high-rise steel structures［J］．China Civil Engineering Journal，2006，39(5):65-71．(in Chinese)

［5］ 王勖成，邵敏．有限单元基本原理和计算方法［M］．北京:清华大学出版社，1997．Wang Xucheng，Shao Min．Theory and algorithm of finite element analysis［M］．Beijing:Tsinghua University Press，1997．(in Chinese)