演化曲线自适应驱动的图像分割水平集模型研究

宋 凌 怡

(四川民族学院 计算机科学系， 四川 康定 626001)



演化曲线自适应驱动的图像分割水平集模型研究

宋 凌 怡*

(四川民族学院 计算机科学系， 四川 康定 626001)

利用图像梯度和几何曲率等信息可以准确定位分割图像的边缘.基于此，本文在对图像分割典型变分模型有效性及所存在问题分析和讨论的基础上，提出了一种演化曲线自适应驱动的图像分割水平集模型.模型通过调整演化曲线长度项和面积项的权重函数，使演化曲线能够根据图像当前的状态自适应的调整演化幅度和方向，不仅提高了图像分割的准确度，还大大缩减了图像分割时间；模型在利用图像局部区域信息的同时，也利用全局化的正则函数来兼顾模型能量泛函的全局性，使模型有了对异质区域边界的捕捉能力.经试验验证文章所提出的新模型有效可靠.

图像分割； 演化曲线； 自适应权重函数； 水平集函数； 能量泛函

图像分割是进行高级图像处理前的重要技术，随着研究的深入，出现了许多经典的图像分割算法[1-2].然而，由于各种图像分割算法的侧重点不同以及分割图像自身含有各种各样的特征数据，分割算法在处理图像噪声、图像边缘定位和降低分割时间等方面都有些不足[3].针对于此，以利用梯度和几何曲率等信息来准确定位图像边缘的基于偏微分方程(PDE)图像分割算法满足了需求.早期基于PDE的图像分割的典型模型主要包括两类：一类是基于边缘信息的分割模型[4]，另一类是基于区域信息的分割模型(主要是CV模型)[5]，前者将图像分割归结为计算一个封闭曲线“能量”泛函的最小化问题，此类模型虽然不会产生图像的边缘断裂，但由于无法准确定位图像边缘，致使分割效果的准确率不是很高；而后者模型利用活动轮廓内外图像信息，不仅一定程度上解决了边缘模糊还减轻了图像噪声干扰，取得了较好的分割效果，但对非同质图像模型图像分割的结果不理想.针对这个问题，国内外有很多学者提出了许多新的模型[6-9]，文献[6，7]利用局部信息很好的解决了上述部分问题，文献[8]中给出了一种处理具有共同边界的多个对象的PC模型，该模型采用双水平集函数并依据“四色定理”对图像进行分割；文献[9]提出的PS模型则是通过两个定义在图像的两个互不相交子区域的光滑函数来逼近待分割的图像.这两个模型都需要根据合理的区域划分来导出水平集演化的偏微分方程组进行求解，其最大缺点是算法复杂性高、演化时间长，因此难以应用于实际问题.此外，文献[10]在CV模型中引入了高斯核函数，把CV模型的全局二值拟合能量泛函改为以高斯函数为核函数的局部二值拟合能量泛函，提出了局部二值能量泛函拟合的LBF(Local Binary Fitting)模型，在一定程度上适应了非同质图像的分割需求，但模型只能采用固定的参数选取模式，无法根据图像的特性自适应分割，所以分割不同类型图像时，分割的精度和速度有不同的效果.

本文在CV模型和LBF模型的基础上，提出了一种演化曲线自适应驱动的图像分割水平集模型，模型通过调整演化曲线长度项和面积项的权重函数，使演化曲线能够根据图像当前的状态自适应的调整演化幅度和方向，提高了演化的精度和速度；此外，模型在利用图像局部区域信息的同时，也利用全局化的正则函数来兼顾模型能量泛函的全局性，使模型有了对异质区域边界的捕捉能力.

1 典型变分模型分析

1.1 Mumford-Shah模型

D.Mumford 和J.Shah将PDE模型应用到图像分割方向，提出了Mumford-Shah变分模型[11].设图像的定义域为u(x)，Ω⊂R2；初始图像I满足：Ω→R，图像分割转化为寻找解(u,C)，且使得下式(1)的能量泛函最小的问题，c⊂Ω为不连续点的集合.

(1)

模型的第一项为保真项；第二项为正则项；第三项是长度项.由于数学处理的困难，第二项正则项和第三项长度项很难找到简单有效的数值逼近，这影响了Mumford-Shah模型的应用，并且在低维测度情况下，由于模型中的两个未知数和以及函数的非凸性，很难解出上式的最小值.

1.2 CV模型

在文献[5]中Chan和Vese对Mumford-Shah变分模型进行了简化，提出了一种CV模型，其能量泛函定义为：

ECV(C，c1，c2)=λ1∬inside(C)|I(x，y)-

c1|2dxdy+λ2∬outside(C)|I(x，y)-c2|2dxdy+
μ·Length(C)+ν·Area(inside(C)),

(2)

其中，inside(C)和outside(C)表示图像在曲线内部和外部的区域，c1,c2分别是图像在这两个区域上的平均灰度值；Length(C)是Euclidean曲线弧长，Area(inside(C))是曲线内部区域面积，λ1,λ2,μ,ν是正值参数.

极小化方程(2)，得到相应的零水平集方程

(3)

进一步，通过求⑶式的稳态解即可得到图像分割结果.

由于表示的是图像在曲线内外部的全局信息，因此模型处理非同质图像的结果不理想.

1.3 LBF模型

(4)

该能量泛函可表示为

(5)

式中，λ1,λ2>0是固定参数，Kσ是带有标准差σ的高斯核，f1,f2分别表示逼近曲线内、外部区域图像局部强度的光滑函数，此时其代替了CV模型中的常数值.相应的水平集函数的演化方程为：

(6)

其中，μ,ν是权系数，其余系数同CV模型.本模型的计算量主要在于-δE(φ)(λ1e1-λ2e2)，其中

(7)

(8)

在模型(6)中，Kσ,μ,ν参数等采用了固定的选取模式.然而大量实验表明，这些参数的改变在很大程度上会影响模型演化的时间以及最后的分割效果，特别对不同类型图像的情况.文献[12]对的选取进行了研究，给出了相应的选择方案.而对于参数μ,ν，目前还仅限于通过大量实验进行人工统计来确定.

1.4 分析与讨论

Mumford-Shah模型通过对图像中边缘跳跃部分进行几何测度予以控制，加之在低维测度下的多个未知数，使数值求解变得比较棘手； CV模型假定图像是由目标和背景两个同质区域组成的，故而将目标和背景看作常数，这样利用分段常数函数来拟合图像.而LBF模型主要是在CV模型的基础上引入了高斯核函数，在一定程度上弥补了CV模型处理非同质区域的不足，除此之外，模型中功能项权重选择对图像的非自适应性，会进一步影响分割的精度和速度.

2 新模型的提出

2.1 水平集函数偏离符号距离函数分析

在原始的几何活动轮廓模型中，水平集函数在演化过程中必须始终保持近似于符号距离函数，这样才能保证水平集演化的稳定性和结果的有效性.

距离保持水平集方法是在传统CV模型的能量泛函中添加了一项内部能量泛函(也叫纠正项)，用以纠正水平集函数与符号距离函数的偏差.如文献[10，13]引入了

(9)

作为水平集函数的内部能量泛函，用于表示水平集函数偏离符号距离函数的程度，用以纠正水平集函数与符号距离函数的偏差.

符号距离函数有如下性质[14]：1)满足|φ|=1；2)满足|φ|的函数φ一定可以表示为一个符号距离函数与一个常数之和.因此对纠正函数进行极小化可以有效防止水平集函数偏离符号距离函数.在新模型继续沿用此项.

2.2 模型的建立

本文建立的模型为：

(10)

式中,第一项为纠正项，用以纠正水平集函数的误差；第二项是Euclidean长度项，用以控制演化曲线的长度来使零水平集逐渐变得平滑，从而减少尖点、角点、奇异点；第三项是面积项，用以控制演化曲线的面积，这样可以使零水平集收缩自如，以实现图像的快速分割；第四项是局部演化拟合项.

具体求解过程：在水平集方法中，C⊂Ω用Lipschitz函数的零水平集表示：

(11)

引进Heaviside算子H和一维Dirac函数δ(z)，则有：

纠正项：

(12)

Euclidean长度项：

(13)

面积项：

Area(inside(C))=Area(φ≥0)=

∬ΩH(φ)dxdy，

(14)

局部演化拟合项：

(15)

新模型的能量泛函E′(f1，f2，φ)表示成：

(16)

固定φ，关于f1,f2极小化能量泛函E′(f1,f2,φ)，根据Euler-Lagrange方程得到：

(17)

在f1和f2固定的条件下，根据Euler-Lagrange方程相对于做E′(f1，f2，φ)的最小化，从而得到新模型的水平集演化方程：

(18)

其中,μ,λ1,λ2是常量权系数，

(19)

定理1模型(10)收敛并存在极小解.

下面证明存在一个收敛的子序列In收敛到I，即In→I.

另外，由高斯核函数的性质有：

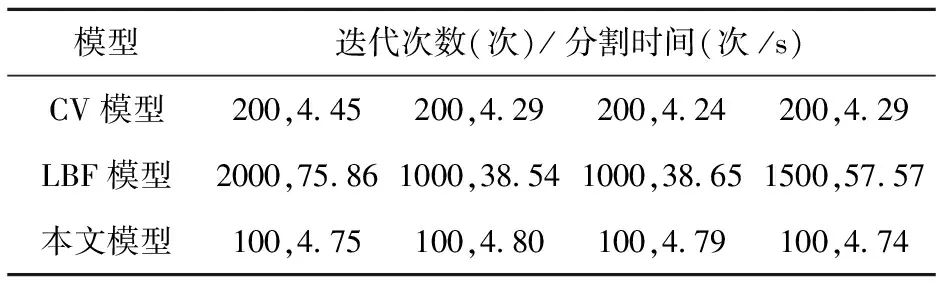
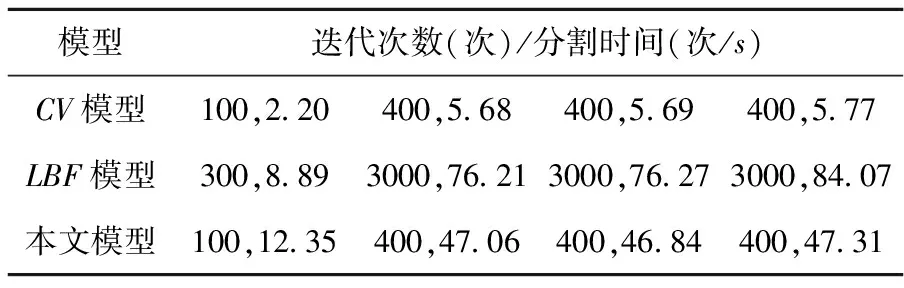
0

在Ω1中，

∬Ω1Kσ(x-y)|In-f1(x)|2H(φ)dxdy

在Ω2中，

∬Ω2Kσ(x-y)|In-f2(x)|2H(φ)dxdy

其中，Mi,j=1,2,3,4,5都是常数.

综上，可以得到如下结论：

(20)

其中,ν(In)，γ(In)也有界，N为常数.

通过均值不等式：|In|≤|In-I|+|I|，其中|I|为常数，可知|In|是有界的.

所以In在Sobolev里是有界且收敛的，那么E肯定存在一个极小解.从而本文所建立的模型存在极小解.

1)长度项与面积项的权重函数

为了减少实际误差，模型中对长度项和面积项增加了自适应特性的权系数函数ν(I)和γ(I)：

(21)

其中，I表示当前图像，sign(·)为符号函数，Gσ是标准差为σ的高斯滤波器，Gσ*I表示对图像I做高斯滤波，Δ为Laplace算子，为梯度算子.

分析：

①针对图像的现行状态和当前特性，需要自适应的控制长度项的大小，而图像信息中的梯度恰恰能反映图像边缘的变化，这样就采用高斯核卷积作为长度项的权重函数，一方面降低了将噪声作为假边缘的可能性，另一方面当零水平集运动到目标边缘附近时，梯度值较大，从而使|(Gσ*I)|的值也较大，这极大地提高了零水平集检验物体多层轮廓的可能性，同时也提高了对深度凹陷区域与多目标物体边缘的捕获能力.

②也需要自适应的控制面积项大小和方向的变化.这里利用权重函数γ(I)[15]从>0和<0两个方向使水平集向目标边缘靠近，以降低演化曲线对初始位置的依赖.

2)δε(φ)函数的选取

文献[16]和文献[13]采用的正则化Dirac 函数δε(φ)是具有紧支集的函数，函数通过限制图像边缘检测的全局性，从而使演化曲线约束在局部.本文提出的模型采用正则化Heaviside和Dirac函数[12]：

(22)

2.3 模型的计算

新模型的计算成本主要在e1,e2中的f1,f2，我们可以通过变形(8)减少计算量，改变形式如下[17]：

(23)

f2的卷积项Kσ*I(x)与Kσ*I是常数，整个演化过程只需计算一次；f1,f2共用Kσ*[Hε(φ)I(x)]与Kσ*Hε(φ)，在每次演化中只需计算一次.这样虽然f1,f2的计算量远小于LBF模型中的(λ1e1-λ2e2)，但分割效果却是相同的.

3 实验结果及分析

为了检验本文所提出模型的有效性，实验各种图像，并将结果与CV模型、LBF模型进行了比较.LBF模型[17]主要参数的取值为μ=1.0，σ=3.0，ε=1.0，时间步长为τ=0.1；本文算法的参数主要为μ=1.0，ε=1.0，τ=0.1.

3.1 多目标图像情况

图1给出了不同算法对多目标Rice图像的分割结果，其中，LBF模型中ν=0.002×255×255，本文模型中选取σ=3.0.从实验结果可以看到，本文方法对初始曲线的选取具有很好的鲁棒性，无论选在何处都能很好的分割出米粒，并且从表1中可以明显看出，本文的分割时间与CV模型接近，大大优于LBF模型；而LBF模型则在所选取的不同初始位置分割米粒的效果都很差；CV模型对左下米粒的分割效果不好，初始位置影响了演化曲线的选取，并且受限于局部最小，导致有时不能实现分割，分割结果可见图1中的CV模型的第3和第4张分割图.

图1 对多目标Rice 图像(128×128)的分割结果对比Fig.1 The multi object Rice image (128 × 128) comparison of segmentation results

表1 图1所对应的分割效率

3.2 内外轮廓情况

图2给出了不同算法对细胞图像的分割结果.其中，图2的LBF模型中ν=0.003×255×255，模型选取σ=4.0.从分割后的图像可以看出：本文所提出的模型能很好将细胞的内外轮廓分割出来，那怕是细胞外部细微的结构也能很好的分割，对不同的初始轮廓进行分割，也能得到较好的分割效果.而在CV模型下，细胞部分实现了较好分割，但有些却陷入局部极小无法分割，细微结构的处理上也不尽人意.从表2分割效率上看，新模型的分割时间优于LBF模型.

图2 对细胞图像(62×50)的分割结果对比Fig.2 The cell image (62 × 50) comparison of segmentation results

表2 图2所对应的分割效率

3.3 异质图像情况

图3是不同算法对异质图像的分割结果，其中在LBF模型中选取ν=0.003×255×255，本文模型中选取σ=10.0.可以看出，本文模型对于所选取的不同的初始轮廓均取得了比较满意的分割结果；而LBF模型和CV模型的分割结果不能令人满意，CV模型的全局性错把部分背景当成目标，出现分割偏差；LBF模型与初始位置有关，只有在正确的位置才能实现较好分割，此外，从表3中可以看出，本文的分割效率总体上要好于LBF模型.

图3 对异质图像(127×96)的分割结果对比Fig.3 The heterogeneous image (127 × 96) comparison of segmentation results

表3 图3所对应的分割效率

4 结论

本文在对CV模型和LBF模型分析和讨论的基础上，提出了提出了一种演化曲线自适应驱动的图像分割水平集模型， 模型借鉴了LBF模型中的纠正项，避免了水平集函数重新初始化，同时通过调整演化曲线长度项和面积项的权重函数，使演化曲线能够根据图像当前的状态自适应的调整演化幅度和方向，大大降低了分割所需时间；此外，模型在利用图像局部区域信息的同时，也利用全局化的正则函数来兼顾模型能量泛函的全局性，使模型有了对异质区域边界的捕捉能力.多次试验结果可以得出，新模型分割图像的效果比CV模型更加细腻、准确，相比LBF模型，分割效果更好更稳定，并且在分割效率上明显优于LBF模型.

[1] 段瑞玲， 李庆祥， 李玉和. 图像边缘检测方法研究综述[J].光学技术，2010， 31 (3):415-419．

[2]ZiouD，TabboneS.Edgedetectiontechniques-anoverview[J].InternationalJournalofPatternRecognitionandImageAnalysis， 2008， 8(4):537-559．

[3] 管宏蕊， 丁 辉. 图像边缘检测经典算法研究综述[J].首都师范大学学报:自然科学版， 2009， 30(10):66-69．

[4]KassM，WitkinA，TerzopoulosD.Snakes:activecontourmodels[J].InternationalJournalofComputerVision， 2011， 1(4): 21-331．

[5]ChanTF，VeseLA.Activecontourswithoutedges[J].IEEETransactionsonImageProcessing， 2011， 10(2): 266-277．

[6]QiGe，LiangXiao，JunZhang，etal.Animprovedregion-basedmodelwithlocalstatisticalfeaturesforimagesegmentation[J].PatternRecognition， 2012， 45(4): 1578-1590．

[7]QiGe，LiangXiao，JunZhang，etal.Arobustpatch-statisticalactivecontourmodelforimagesegmentation[J].PatternRecognitionLetters， 2012， 33(12): 1549-1557．

[8]VeseLA，ChanTF.Amultiphaselevelsetframeworkforimagesegmentationusingthemumford-shahmodel[J].InternationalJournalofComputerVision， 2012， 50(3): 271-293．

[9]TsaiA，YezziA，WillskyAS.Curveevoluationimplementationofthemumford-shahfunctionalforimagesegmentation，denoising，interpolation，andmagnification[J].IEEETransactionsonImageProcessing， 2011， 10(8): 1169-1186．

[10]LiCM，KaoCR，GoreJ，etal.Implicitactivecontoursdrivenbylocalbinaryfittingenergy[C]//ProceedingsofIEEEConferenceonComputerVisionandPatternRecognition.Minneapolis，MN，USA:IEEE， 2007: 1～7．

[11]MumfordD，ShahJ.Optimalapproximationsbypiecewisesmoothfunctionsandassociatedvariationalproblems[J].Commun.PureApplMath， 2009， 42(5): 577-685．

[12] 原 野， 何传江.LBF活动轮廓模型的改进[J].计算机工程与应用， 2009， 45(15):177-180．

[13]LiC，XuC，GuiC，etal.Levelsetevolutionwithoutre-initialization;anewvariationalformulation[C]//ProcoftheIEEEComputerSocietyConfoncomputerVisionandPatternRecognition.NewYork, 2010:430-436．

[14]OsherS，FedkiwR.LevelSetMethodsAndDynamicImplicitSurface[M].NewYork:Springer-Verlag， 2012．

[15] 何传江， 李 梦， 詹 毅. 用于图像分割的自适应距离保持水平集演化[J].软件学报， 2008， 19(12): 3161-3169．

[16]HONG-KaiZhao，ChanT，MerrimanB，etal.Avariationallevelsetapproachtomultiphasemotion[J].JournalofComputationalPhysics， 1996， 127(1):179-195．

[17]LiCM，KaoCY，GoreJ，etal.Minimizationofregion-scalablefittingenergyforimagesegmentation[J].IEEETransactionsonImageProcessing， 2011， 17(10): 1940-1949．

A level-set model for image segmentation with adaptively driven evolutional curve

SONG Lingyi

(Department of Computer Science， Sichuan University for Nationalities，Kangding，Sichuan 626001)

Image segmentation model based on partial differential equation is widely concerned， because it can accurately locate the edge of object by directly using image’s geometric information such as gradient， curvature， and etc. In this study， we first discuss the effectiveness and disadvantages of state-of-the-art variational models for image segmentation. Based on our analysis， we subsequently propose a novel level-set model for image segmentation with adaptively driven evolutional curve. The features of the proposed model are as follows. According to current state of the image， the evolutional curve is able to adaptively adjust evolution amplitude and direction by introducing a weighting function of length and area terms. This both improves segmentation accuracy and reduces time to obtain ideal segmentation results， While depending on the local image information， a global regular function is employed to balance the global feature of energy functional so as to enhance the model’s ability to capture edges of heterogeneous area. Experimental results verify the effectiveness of the proposed model．

image segmentation; evolution curve; adaptive weighting function; level set function; energy function

2014-09-22.

1000-1190(2015)02-0195-06

TP391

A

*E-mail: Gslyst5201@163.com.