一类特殊三角函数的最大值解

周桂如

（福建船政交通职业学院基础教研室，福建福州350007）

一类特殊三角函数的最大值解

周桂如

（福建船政交通职业学院基础教研室，福建福州350007）

首先在△ABC中，给出特定系数的最大值问题，分别利用逐步分析法、拉格朗日乘数法和不等式三种方法获得相同的结果，然后利用拉格朗日乘数法推导出任意系数三角函数（其中）的最大值求解方法，最后推导三角函数（其中）的极值。

拉格朗日乘数法；逐步分析法；极值

引言

最值和不等式，是数学组成的重要内容和部分，不等式揭示变量之间的制约关系，而最值问题与它紧密相关。三角函数的最值问题是函数最值问题的一个重要部分。解答三角函数的最值问题，除了要用到代数中求最值问题的定理和方法外，通常还要借助三角函数的一些特性来求解。

引理1[1]：，当其中时取得最大值。

引理2[2]：在任意△ABC中有

引理3[3]：对及及任意△ABC有当且仅当且时等号成立。

引理4[4]：设函数在点的某邻域内具有二阶连续偏导数，且点是函数的驻点，即，记：则：

1 主要结果

1.1 逐步分析法[5]

三角形三个角A、B、C的取值范围为

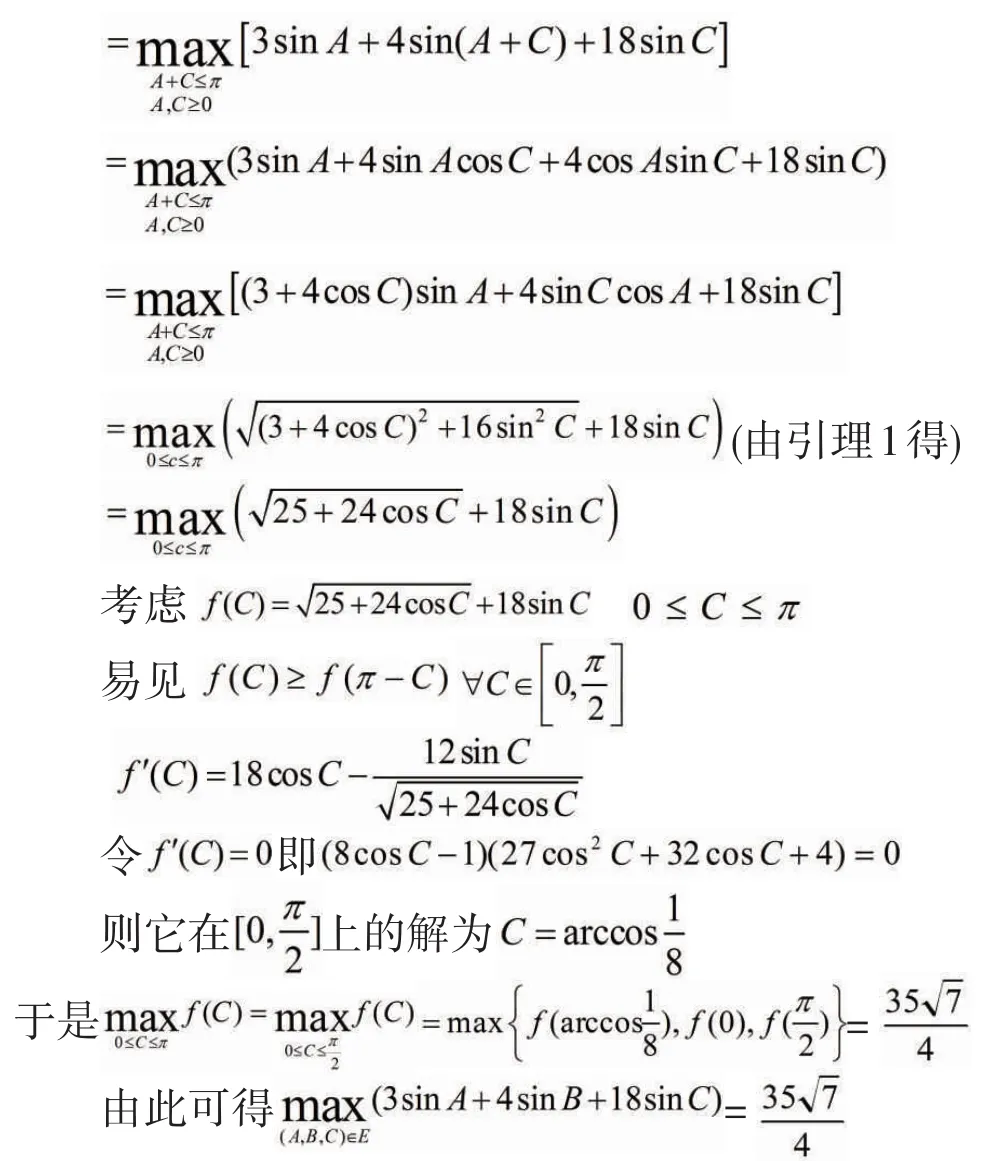
1.2 用拉格朗日乘数法

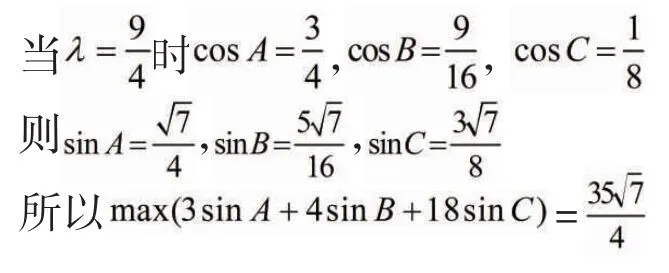
1.3 不等式法

2 一般形式的三角函数极值

2.1 对于△ABC，（其中）的极值

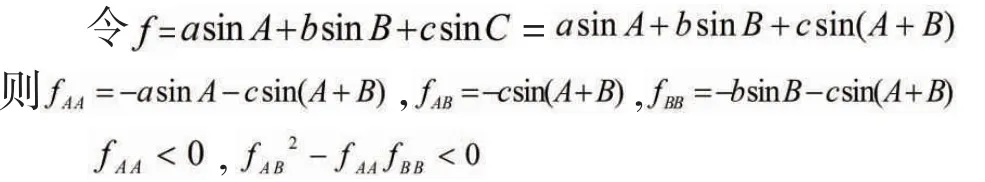
根据拉格朗日乘数法

2.2 对于△ABC，（其中的极值

根据拉格朗日乘数法

3 结语

三角函数最值问题题型丰富多彩，其解法也层出不穷。例如利用三角函数的有界性、换元法、判别式法、利用函数的单调性、对含参数的三角函数最值的分类讨论法、利用基本不等式法（如：和差化积与积化和差公式、均值不等式、柯西不等式）等都是解三角函数最值的常用手段,解决这类问题关键是在于对三角函数的灵活应用，抓住关键和本质所在。

注释及参考文献：

[1]数学教材研究开发中心．普通高中课程标准实验教科书[M]．北京：人民教育出版社，2004：35-40．

[2]裴礼文．数学分析中的典型问题与方法[M]．北京:高等教育出版社,1993,267-287．

[3]杨学枝．关于三角形的两类不等式[J]．湖南教育学院学报，1999,17(2):32-37．

[4]华东师范大学数学系．数学分析第三版[M]．北京:高等教育出版社,2003．

[5]胡中双．浅谈高中数学教学中创造性思维能力的培养[J]．湖南教育学院学报，2001,19(4):147-148．

The Solution to Maximum Value of a Special Class of Trigonometric Functions

ZHOU Gui-ru
（Department of Basic Teaching,Fujian Chuanzheng Communications College,Fuzhou，Fujian 350007）

For the maximum value of a trigonometric functionwith special coefficients in△ ABC,three solutions of analysis segment,the Lagrange multiplier,the inequalities,are first proposed,leading to the same result.Then for a general trigonometric functionwith the coefficients,b,andcbelonging to，the Lagrange multiplier is used to seek its maximum value.Finally,the solution to the extreme value of the trigonometric functionwith the coefficients,b,andcbelonging tois derived.

Lagrange multiplier;analysis segment;extreme value

O174

A

1673-1891（2015）03-0012-03

2015-05-03

周桂如（1980-），女，硕士，讲师，主要从事应用数学方面的研究。