基于动态波动系数的风电功率平滑控制策略*
袁桂丽,刘 颖,陈少梁
(华北电力大学,北京 102206)
基于动态波动系数的风电功率平滑控制策略*
袁桂丽,刘 颖†,陈少梁
(华北电力大学,北京 102206)
风力发电的随机波动对电力系统的稳定性带来不利影响,通过配备储能系统可以提升电网接纳风电的能力。本文定义了反映储能系统平抑风电波动效果的波动系数;提出一种基于动态波动系数的风电功率平滑控制策略;建立了以波动系数为优化变量,风电实际功率和并网功率的差值最小为目标,并网功率波动要求为约束的优化模型;设计了基于滑动窗口的遗传算法求解方案,优化求得动态波动系数及相应的储能额定容量及功率,最终利用储能抑制风电功率的波动。实验表明,与传统控制策略相比,该策略能有效抑制功率波动并降低储能容量,节约成本。
风力发电;储能系统;平抑控制;波动系数
0 引 言
风力发电具有随机性和波动性,其并网会对电网产生冲击,一旦超出了波动范围,会严重破坏电网的安全性和稳定性[1-2]。为风电场配置一定容量的储能系统(Energy storage system, ESS)能够平抑风电波动,使输出功率满足一定指标[3-4]。鉴于目前储能装置的成本较高且寿命较短,如何利用有限容量的储能系统平抑功率的波动性,对控制算法提出了较高的要求,通过控制算法优化获得合理的储能系统容量及出力是十分重要的问题。
文献[5-6]将风电输出功率设置为某一定值,通过电池储能补偿波动,这种方法可以满足电网功率波动要求,但需要的储能容量大,成本过高。为此,基于滤波算法及改进的滤波算法控制策略相继被提出[7-11],但基于滤波算法的控制策略均存在一定滞后,这导致系统所需储能容量加大,充放电深度加深。本文兼顾平滑效果并降低储能成本,设计基于波动系数的控制算法,利用较小储能容量,实现风电输出功率的平滑控制。
1 风电功率平抑策略及建模
利用储能对风电输出功率进行平抑处理,其基本原理是通过调节储能系统的输出功率,对风电功率中波动较大的成分进行补偿,以获得较为平滑的风电并网功率。不同的控制策略使储能系统充放电指令不同,直接影响到储能装置容量的大小。
1.1 平抑策略的提出
风电实际功率与并网功率的偏差决定了储能系统的充放电指令。并网功率越接近实际输出功率,意味着储能系统补偿的功率越小,所需安装的储能装置容量也越小。假设系统的功率指令序列分别表示如下:

式中,Pwind表示风电场实际输出功率序列,Pgrid表示并网功率序列,Pess表示储能系统功率指令序列;Pwind,t、Pgrid,t、Pess,t分别表示t(t=1, 2, … n)时刻系统各功率输出值。t时刻系统功率输出关系为:

当Pess,t>0时,表示储能系统放电;当Pess,t<0时,表示储能系统充电。
风力发电功率曲线斜率的大小直接反应了功率的波动情况。设Δt为采样时间间隔,t~(t+Δt)时刻的斜率越大,意味着该时段功率的变化率越大,波动的幅度越明显。若某时段风电输出功率的波动超过电网所能承受的范围,则需利用储能系统补偿波动,降低功率的变化幅度。因此定义波动系数ωt,令:

式中:ωt∈[0, 1],该参数表征了并网功率的波动大小,同时也确定了储能系统的充放电指令。
由此,储能平抑波动的效果关键在于波动系数的选取。ωt=0时,平抑目标功率在t~(t+Δt)时段的斜率为0,风电功率的波动由储能系统完全补偿,此时平抑效果最佳,可以一直保持波动为0,但储能输出的幅值大,系统对储能容量的要求高;ωt=1时,平抑目标功率在t~(t+Δt)时段的斜率等于实际功率的斜率,储能系统不动作,此时平抑效果最差,但不需要投入储能,系统对储能容量无要求。
1.2 模型的建立
为了降低系统对储能设备容量的要求,减少成本,应适当选取波动系数,得到满足功率波动指标的平抑目标功率,并使计算结果尽可能地接近风电实际功率。利用智能优化算法求解该问题,关键在于确定目标函数和约束条件。
1.2.1 目标函数
本文以安装的储能容量最小为目标。储能设备的功率输出值等于并网功率和实际功率的差值。所以这个差值越小,则所需储能设备的容量越小,成本也就越低。从功率曲线上看,就是尽可能地使得并网目标功率接近风电场的实际输出值。定义目标函数为:

式中,Pgrid,t(ωt)表示t时刻平抑后的并网目标功率,随ωt变化;n为计算时间尺度内的采样点数。
1.2.2 约束条件
风电功率的波动一般用爬坡率来描述,爬坡率即电功率的变化幅度占额定功率的百分比。研究表明,不同时间尺度的风电功率波动对电网的不同方面(如系统备用、能量调度以及安全运行等)造成的影响不同。许多国家要求风电输出功率要同时满足在几个不同时间尺度下的爬坡率指标。利用储能技术可以平抑不同时间尺度下的功率波动,保证风电输出功率的可控性,从而使大规模风电并网成为可能。表1是几个国家的电功率波动指标[12]。

表1 各国风电并网电功率波动指标[12]Table 1 Fluctuation index of different countries[12]
为了使系统满足并网功率要求,本文采用两个时间尺度的爬坡率指标作为该问题的约束条件:
(1)每分钟的波动幅度不超过系统额定功率的2%;(2)每10 min的波动幅度不超过系统额定功率的20%。表达式如下:

式中,Pgrid,t−1表示t−1时刻并网目标功率; max(Pgrid,t~t+9) 和min(Pgrid,t~t+9) 表示10 min内并网目标功率的最大值和最小值;k1和k2表示功率波动指标1 min和10 min的最大爬坡率;Pr表示风力发电额定功率。
2 求解步骤
本文提出的控制系统采样周期为1 min,为了避免优化过程中约束条件过多,采用滑动窗口的方法进行波动系数ωt的动态寻优,获得一段时间内满足电网功率波动要求的最小储能输出。由于系统需要同时满足1 min和10 min的爬坡率指标约束,设定滑动窗口宽度Nt为10。

图1 基于滑动窗口的遗传算法求解步骤Fig. 1 Genetic algorithm based on sliding window
取t时刻及t时刻之前连续的Nt−1个风电功率数据,建立如式(4)、式(5)所示变量为ωt的优化模型,利用遗传算法获得波动系数的最优值ωt,将其作为t时刻的波动系数,从而获得最小Pess,t。按点距移动窗口,重复此优化方法,直到对整体数据完成上述过程。算法流程如图1所示。由图中流程可知,本文提出的控制策略不仅能够对历史数据进行处理,获得系统所需最小的储能容量;同样也适用于风电功率波动的实时平抑。
3 储能装置容量计算
蓄电池是世界上广泛使用的一种化学“电源”,具有电压平稳、安全可靠、价格低廉、适用范围广、原材料丰富和回收再生利用率高等优点,是世界上各类电池中产量最大、用途最广的一种电池。本文采用蓄电池作为储能单元来平抑风电的波动。
3.1 额定功率
设在计算时间尺度内,蓄电池的输出功率指令序列为:Pess=[Pess,1,…,Pess,n];考虑到系统的充放电效率,储能系统实际充放电功率指令序列为:PESS=[PESS,1,…,PESS,n]。则两者关系表达式为:

式中,η1、η2分别表示蓄电池放电和充电效率;n表示采样点数。
在整个周期内,储能所需补偿功率绝对值的最大值即为储能的额定功率[10]:

3.2 额定容量
获得储能系统实际充放电功率指令后,可计算不同时刻储能相对于初始时刻的充放电能量:

式中,Δt表示采样时间间隔,n表示采样点数。
假设蓄电池额定容量为Er,初始时刻荷电状态为SOC(0),则不同时刻储能装置的荷电状态SOC(t)表示为:

充电时E(t)为负,剩余能量增加,SOC(t)增大;反之,放电时E(t)为正,剩余能量减小,SOC(t) 降低。
设储能系统荷电状态最大和最小允许值分别为SOCmax和 SOCmin,则:

式中,Er1和Er2分别表示SOC最大和最小是系统所需储能容量。为同时满足荷电状态上限和下限的约束,蓄电池所需额定容量应取上述两个数值的较大值,即:

4 算例分析
4.1 采取波动系数的控制策略分析
算例采用某额定功率为10 MW的风电机组某天的实际输出功率数据。按图1的流程图,利用遗传算法对模型求解。
风电场实际输出功率和目标功率如图2所示。可以发现目标功率明显比实际输出功率少了很多波动量,功率曲线变得更为平滑。图3是按式(2)计算得出的储能系统期望出力。

图2 基于波动系数平抑算法的平抑控制输出Fig. 2 Curves of smoothing control output based on fluctuation coefficient

图3 储能系统期望充放电功率Fig. 3 Charge-discharge power of ESS
图4和图5是目标功率的1 min和10 min波动率。可见,图4中目标功率1 min波动率不超过2%;图5中目标功率的10 min最大波动率为18%。显然,两个时间尺度的波动率均满足系统并网要求。

图4 目标平抑功率1 min波动率Fig. 4 The 1 minute fluctuation rate of grid connected power
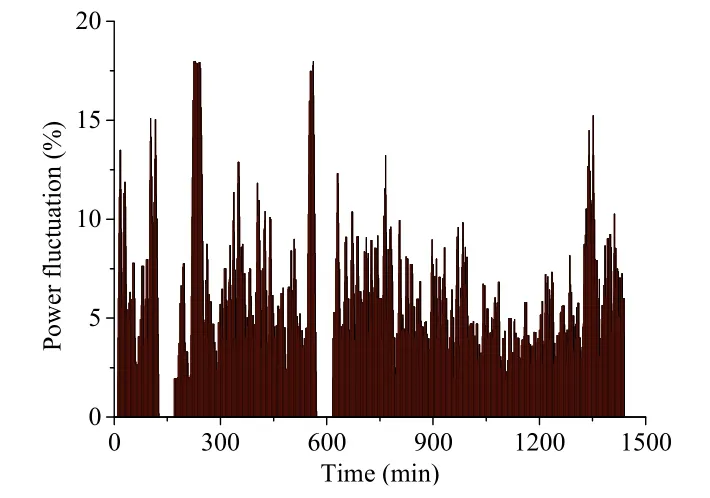
图5 目标平抑功率10 min波动率Fig. 5 The 10 minute fluctuation rate of grid connected power
图6和表2分别给出了采用动态和固定波动系数时系统的参数对比。对比可知,为了使并网功率同时满足两个时间尺度的波动要求,固定波动系数应设为0.4,所需配置的储能额定功率和容量分别为2.937 5 MW和3.573 5 MW·h;而采用动态波动系数的控制策略更加灵活,仅需配置1.919 2 MW和1.446 9 MW·h的储能,虽然波动率略有增加,但完全满足电网要求,并大大减少了储能容量和充放电总量,降低了系统成本,延长了储能装置使用寿命。

图6 波动系数取值Fig. 6 Value of fluctuation coefficient
从这些图表可以发现,利用本文控制策略平抑波动后,风电平抑目标输出功率完全满足两个时间尺度上的波动指标。本文所提出的方法兼顾了平滑效果并有效减少了储能容量。

表2 固定波动系数参数对比Table 2 Comparison of fixed fluctuation coefficient
4.2 与其他控制策略的性能比较
采取与 4.1 节相同的算例,对比基于本文控制策略及其他传统控制策略的平抑效果。对比结果如表3所示。结果显示,为了达到风电并网功率波动要求,采用一阶低通滤波算法需要配置的储能装置容量较大,且储能系统充放电总量相当于本文策略的两倍,这使得储能装置频繁动作,降低了储能的使用寿命;而利用最小二乘算法虽然所需配置的储能容量较少,但功率波动明显增加,储能充放电总量相对本文策略较大,不利于储能装置长期使用。可见,相比于传统控制策略,本文所提出的控制策略在电池容量需求和电池总充放电量上都有了大幅度的改善。

表3 基于不同控制算法的对比Table 3 Comparison of different control algorithms
5 结 论
为风电场配备储能系统可有效平滑风电功率的波动。本文提出一种基于动态波动系数的风电功率平抑控制策略,可在间歇性电源输出的波动功率中实时寻找使电池充放电电量之和最小的参考点,满足风电并网功率波动要求的同时,降低了控制系统对电池容量的需求,减少控制过程中电池的充放电电量。将提出的控制策略应用于风电输出功率实时平滑控制,结果显示,与传统控制策略相比较,本文控制策略在风电功率波动率相近的情况下,明显减少了所需配置的储能容量和充放电总量,有效节约了成本,延长了储能装置的使用寿命。
[1] 康龙云, 郭红霞, 吴捷, 等. 分布式电源及其接入电力系统时若干研究课题综述[J]. 电网技术, 2010, 34(11): 43-47.
[2] SORENSEN P, CUTULULIS N A, VIGUERAS- RODRIGUEZ, A, et al. Power fluctuations from large wind farms[J]. IEEE Trans on Power System, 2007, 22(3): 958-965.
[3] 张步涵, 曾杰, 毛承雄, 等. 电池储能系统在改善并网风电场电能质量和稳定性中的应用[J]. 电网技术, 2006, 30(15): 54-58.
[4] 于芃, 赵瑜, 周玮, 等. 基于混合储能系统的平抑风电波动功率方法的研究[J]. 电力系统保护与控制, 2011, 39(24): 35-40.
[5] 张纯江, 董杰, 刘君, 等. 蓄电池与超级电容混合储能系统的控制策略[J]. 电工技术学报, 2014, 29(4): 334-340.
[6] 周林, 黄勇, 郭珂, 等. 微电网储能技术研究综述[J]. 电力系统保护与控制, 2011, 39(7): 147-152.
[7] YOSHIMOTO K, NANAHARA T, KOSHIMIZU G. New control method for regulating state-of-charge of a battery in hybrid wind power/battery energy storagesystem: Power Systems Conference and Exposition[C]. October 29-November 1, 2006, Atlanta, America: 7p.
[8] 张野, 郭力, 贾宏杰, 等. 基于电池荷电状态和可变滤波时间常数的储能控制方法[J]. 电力系统自动化, 2012, 36(6): 34-38.
[9] 桑丙玉, 王德顺, 杨波, 等. 平滑新能源输出波动的储能优化配置方法[J]. 中国电机工程学报, 2014, 34(22): 3700-3706.
[10] 丁明, 吴建锋, 朱承治, 等. 具备荷电状态调节功能的储能系统实时平滑控制策略[J]. 中国电机工程学报, 2013, 33(1): 22-29.
[11] 谢 涛, 曹军威, 高 田, 等. 基于滑动最小二乘算法和电池荷电状态的储能系统平滑控制策略[J]. 电力系统保护与控制, 2015, 43(5): 1-7.
[12] 全国电力监管标准化技术委员会. GB/T 19963-2011. 风电场接入电力系统技术规定[S]. 北京: 中国质检出版社, 2011.
Smoothing Control Strategy of Wind Power Based on Dynamic Fluctuation Coefficient
YUAN Gui-li, LIU Ying, CHEN Shao-liang
(North China Electric Power University, Beijing 102206, China)
The fluctuation of wind power has a negative effect on the stability of the power system. By using the energy storage system, the ability to accept wind power can be promoted.In this paper, the fluctuation coefficient is defined, which reflects the wind power smoothing effect of energy storage system. Also a fluctuation smoothing control strategy based on dynamic fluctuation coefficient is proposed; taking the minimization of the difference between the actual power and the grid power of the wind power as the objective and the requirements for the fluctuation of grid connected power as constrains, an optimal configuration model is built. A genetic algorithm based on sliding window is designed to solve the problem. Compared with the traditional control strategy, experiments show that the proposed method can effectively smooth the power fluctuation, reduce the storage capacity and save the cost.
wind power generation; energy storage system; smoothing control; fluctuation coefficient
TK81;TK02
A
10.3969/j.issn.2095-560X.2015.05.001
2095-560X(2015)05-0325-06
袁桂丽(1971-),女,博士,副教授,主要从事信息控制、先进控制策略及其应用、电力系统控制与优化调度研究。
2015-07-23
2015-08-10
† 通信作者:刘 颖,E-mail:562982396@qq.com
刘 颖(1991-),女,硕士研究生,主要从事可再生能源与储能接入装备及并网技术研究。
陈少梁(1990-),男,硕士研究生,主要从事可再生能源与储能接入装备及并网技术研究。

