MATLAB在多元函数教学中的应用
MATLAB在多元函数教学中的应用
麻 桂 英
(包头师范学院 数学科学学院,内蒙古 包头 014030)
摘要:多元函数微积分的教学一直都是《高等数学》教学的重点与难点。采用Matlab软件于教学,可以使抽象繁冗的数学理论直观化,具体化,从而激发学生的学习兴趣,提高学习热情。
关键词:极限;偏导数;方向导数;重积分;Matlab; 曲面积分
《高等数学》是理工科院校的一门重要的基础课,其主要研究对象是函数。在《高等数学》上册中我们讨论的函数只有一个自变量,这样的函数称为一元函数;但在很多实际问题中往往牵涉到多方面的因素,反映到数学上,就是一个变量依赖于多个变量的情形,由此提出了多元函数以及多元函数的微分与积分问题。《高等数学》下册的核心内容之一就是多元函数的微积分。尽管多元函数的微积分是一元函数微积分的拓展,但从一元函数到二元函数会产生新问题,而从二元函数到二元以上的多元函数则可以类推,因此讨论中我们以二元函数为主。
由于多元函数的研究已经从线到面甚至空间,教学中学生普遍感到学习困难:教学内容抽象,计算繁杂;而Matlab的优势是它强大的计算能力,在多元函数教学中巧妙借助一些数学软件能使抽象复杂的内容直观化,繁冗的计算与推导简单化。
1计算多元函数的极限
多元函数的极限要比一元函数的极限复杂的多。原因是二元函数的自变量在平面上从四面八方以任意方式趋近于某一目标远比一元函数在直线上只有左右两个趋近方向复杂。

解:求极限的程序:
>> clear
>> syms x y
>> f=(x*y-sin(x*y))/(x*y-x*y*cos(x*y))
f =
(x*y-sin(x*y))/(x*y-x*y*cos(x*y))
>> fx=limit(f,'x',0)
fx =
1/3
>> fxy=limit(fx,'y',0)
fxy =
1/3
2求多元函数的偏导数
尽管多元函数求偏导数的运算法则类似于一元函数的求导法则,但求偏导的计算繁冗,尤其是高阶偏导数。
例2:设z=u2lnv,而u-xy,v=x+y,求z关于变量x及y的一阶偏导数和二阶偏导数。
解:复合函数求偏导数的程序:
>>clear
>>syms x y z u v
>>u=x*y;
>>v=x+y;
>> z=u^2*log(v);
>>dzx=diff(z,'x')
dzx =
2*x*y^2*log(x+y)+x^2*y^2/(x+y)
>>dzy=diff(z,'y')
dzy =
2*x^2*y*log(x+y)+x^2*y^2/(x+y)
>> pretty(dzx),pretty(dzy)
2xy2iog(x+y)+x2y2/(x+y)
2x2ylog(x+y)+x2y2/(x+y)
>> dzxy=diff(dzx,'y')
dzxy =
4*x*y*log(x+y)+2*x*y^2/(x+y)+2*x^2*y/(x+y)-x^2*y^2/(x+y)^2
>> dzxx=diff(dzx,'x')
dzxx =
2*y^2*log(x+y)+4*x*y^2/(x+y)-x^2*y^2/(x+y)^2
>> dzyy=diff(dzy,'y')
dzyy =
2*x^2*log(x+y)+4*x^2*y/(x+y)-x^2*y^2/(x+y)^2
>> dzyx=diff(dzy,'x')
dzyx =
4*x*y*log(x+y)+2*x*y^2/(x+y)+2*x^2*y/(x+y)-x^2*y^2/(x+y)^2
>> pretty(dzxy),pretty(dzxx)
4xylog(x+y)+2xy2/(x+y)+2x2y/(x+y)-x2y2/(x+y)2
2ylog(x+y)+4xy/(x+y)-xy/(x+y)2
3求多元函数的梯度和方向导数
方向导数显示了函数在某点沿着某个方向上的变化率。函数在某点沿某个方向的方向导数等于在该点的梯度与该方向的单位向量的数量积。而模取得最大值的方向导数就是该店的梯度,此时多元函数增加最快。

解:先计算方向导数,程序如下:
>> clear
>> syms x y
>> z=x^2+y^2;
>> v=[1/2,sqrt(3)/2];
>> dxy=jacobian(z)
dxy =
[ 2*x, 2*y]
>>T=dot(dxy,v)
T =
conj(x)+conj(y)*3^(1/2)
>> subs(T,'x',1)
ans =
1+conj(y)*3^(1/2)
>> subs(subs(T,'x',1),'y',2)
ans =
4.4641
再画图像
>>clear
>>x=[-1:0.1:1];
>> [X,Y]=meshgrid(x);
>> Z=X.^2+Y.^2;
>>surf(X,Y,Z)

4计算多元函数的极值
由于二元函数求极值的充分条件需要计算一阶及二阶偏导数,运算量大,因此可用MATLAB优化多元函数的极值与最值问题。
例4:讨论函数f(x,y)=x3-y3+3x2+3y2-9x的极值。
解:先求极值
>> clear
>> syms x y X Y
>> f=x^3-y^3+3*x^2+3*y^2-9*x
f =
x^3-y^3+3*x^2+3*y^2-9*x
>> F=jacobian(f)
F =
[ 3*x^2+6*x-9,-3*y^2+6*y]
>> [X,Y]=solve(F(1),x,F(2),y)
X =
1
-3
1
-3
Y =
0
0
2
2
>> dxx=diff(F(1))
dxx =
6*x+6
>> dyy=diff(F(2))
dyy =
-6*y+6
>> dxy=diff(F(1),y)
dxy =
0
由MATLAB程序知,函数有四个驻点:(-3,0)’(1,0),(-3,2),(1,2);依次判别得函数在(-3,2)处有极大值31;在(1,0)处有极小值-5;其它驻点处无极值。
5计算三重积分

>> clear
>> syms x y z
>> f=z;
>> A=int(int(int(f,z,x^2+y^2,2),y,0,sqrt(2-x^2)),x,0,sqrt(2))
A=
2/3*pi
6计算曲面积分
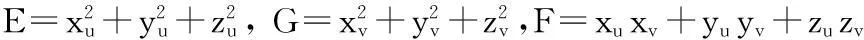
>>clear
>> syms Q V x y z a
>> x=a*cos(Q)*sin(V);y=a*sin(Q)*sin(V);z=a*cos(V);
>> dxQ=diff(x,Q);dxV=diff(x,V);
>> dyQ=diff(y,Q);dyV=diff(y,V);
>>dzQ=diff(z,Q);dzV=diff(z,V);
>>E=dxQ^2+dyQ^2+dzQ^2
E =
a^2*sin(Q)^2*sin(V)^2+a^2*cos(Q)^2*sin(V)^2
>>G=dxV^2+dyV^2+dzV^2
G =
a^2*cos(Q)^2*cos(V)^2+a^2*sin(Q)^2*cos(V)^2+a^2*sin(V)^2
>>F=dxQ*dxV+dyQ*dyV+dzQ*dzV
F =
0
>> dS=sqrt(E*G-F^2)
dS =
((a^2*sin(Q)^2*sin(V)^2+a^2*cos(Q)^2*sin(V)^2)*(a^2*cos(Q)^2*cos(V)^2+a^2*sin(Q)^2*cos(V)^2+a^2*sin(V)^2))^(1/2)
>>dS=simplify(dS)
dS=
(-a^4*(-1+cos(V)^2))^(1/2)
>> f=x+y+z
f=
a*cos(Q)*sin(V)+a*sin(Q)*sin(V)+a*cos(V)
>> I=int(int(f*dS,Q,0,2*pi),V,0,pi/2)
I=
1/(a^4)^(1/2)*a^5*pi
>> simple(I)
simplify:
csgn(a^2)*a^3*pi
radsimp:
a^3*pi
在《高等数学》下册多元函数的教学中,融数学软件与教学,大胆尝试,不断探索,勇于创新是提高教学质量的必由之路。
〔参考文献〕
[1]同济大学数学系编.高等数学(第六版)[M].北京:高等教育出版社,2008,4.
[2]周珑.高等数学全程导学及习题全解(第五版)[M].北京:中国时代经济出版社,2006,9.
[3]张学山等.高等数学实验[M].上海:华东理工大学出版社,2006,9.
[4]李磊.浅谈多媒体辅助教学的利弊[J].长春理工大学学报,2008,3.
[5]肖海军等.数学实验初步[M].北京:科学出版社,2012,2.
[6]刘正君.MATLAB科学计算宝典[M].北京:电子工业出版社,2012,5.
[7]大学数学编写委员会编.高等数学[M].北京:科学出版社,2013,6.
[8]麻桂英.大一新生《高等数学》教学策略的探究[J].阴山学刊,2014,2.
Application of MATLAB in Multi Function Teaching
MA Gui-ying
(Faculty of Mathematic,Baotou Teachers College,Baotou 014030)
Abstract:The calculus teaching of many variables function has been the key points and difficulties of higher mathematics.Using Mat lab software in teaching can make the abstract mathematical theory of lifting, visualizations, and specific, so as to stimulate students' interest in learning, improve their learning enthusiasm.
Key words:limit; partial derivatives.directional derivative; double Integrals; Matlab; surface integral
中图分类号:O242
文献标识码:A
文章编号:1004-1869(2015)02-0063-04
作者简介:麻桂英(1969-),内蒙古鄂尔多斯市人,副教授,研究方向:高等数学教学。
收稿日期:2014-11-04

