某车型盘式制动器制动噪声优化分析

付广,梁静强,刘忠伟,吕俊成

(上汽通用五菱汽车股份有限公司,广西柳州 545007)

某车型盘式制动器制动噪声优化分析

付广,梁静强,刘忠伟,吕俊成

(上汽通用五菱汽车股份有限公司,广西柳州 545007)

结合复模态分析理论和有限元法，通过Abaqus软件，建立某车型盘式制动器的有限元模型，计算出该模型20 kHz以内的复模态，根据复特征根实部为正值判断出制动器产生不稳定性，即在制动的时候有发生制动噪声的倾向。计算结果和测试结果比较吻合，验证了模型的准确性。提出了针对制动钳体和摩擦片结构的改进措施，对改进后的模型进行分析，结果表明：改进后的制动器没有出现不稳定模态。

盘式制动器；制动噪声；复模态分析；有限元

0 引言

盘式制动器在制动过程中发生振动从而产生制动噪声。制动过程中，摩擦片发生振动，而制动鼓和制动钳刚度较小，振动被放大，形成一个较大的声源，同时摩擦片和制动盘接触恶化，摩擦力不断变化，制动器受到持续交变力的作用而产生自激励，发生连续噪声。制动噪声的频率范围非常宽，从几十赫兹到上万赫兹，通常研究者将制动噪声分类为1 kHz以内的低频颤振噪声和1 kHz以上的制动尖叫噪声[1]。研究摩擦噪声的产生机制是研究制动噪声的根本方法，从20世纪50年代以来，许多学者对摩擦噪声形成机制进行过系统的研究，一般分为4种，分别为黏着-滑动机制、自锁-滑动机制、摩擦力-相对滑动速度负斜率机制和模态耦合机制。这四种机制又可分为两类：黏滑机制和结构的不稳定机制，他们都认为制动系统的振动以及伴随的噪声是由于摩擦界面上变化的摩擦力引起制动系统的不稳定产生的[2]。

文中以某车型盘式制动器为研究对象，结合复模态分析理论和有限元方法，建立了盘式制动器有限元分析模型，对盘式制动器进行复模态分析，并与测试结果进行对比，验证了模型的准确性，通过对复模态结果的分析，提出了制动钳体和摩擦片结构改进措施，抑制了制动噪声发生的倾向。

1 制动器复模态分析理论

制动器制动过程主要是靠摩擦片和制动盘之间的摩擦力来实现制动，由于摩擦耦合诱发和制动器各部件的模态参数匹配不当而引起制动系统不稳定，而运动系统的特征值实部和不稳定模态相对应，可以通过提取复模态特征值从而确定出制动系统不稳定模态。

盘式制动器运动方程：

(1)

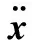
制动盘和摩擦片之间的摩擦力矩阵可表示为：

Ff=Kfx

(2)

式中：Kf为摩擦耦合刚度矩阵。

因此制动器运动方程可改写为：

(3)

由于矩阵Kf是由制动盘和摩擦片之间的摩擦引入的非对称刚度矩阵，它耦合了二者之间的法向相对位移和切向力，故整个系统刚度矩阵也为非对称矩阵，方程(3)在实空间里无法解耦，只能按照复模态理论进行解耦。从物理意义上讲，刚度矩阵的不对称达到一定程度时，可能导致系统内部的能量馈入，从而成为发散系统，系统在微小的扰动下可能出现振幅越来越大的振动，产生不稳定，从而出现制动噪声[3]。从以上方程计算出系统各阶模态频率和模态振型都是复数，模态频率复数的虚部反映了振动时的固有频率，实部反映了系统运动的稳定性，若实部为正数，说明该阶模态的阻尼比为负数，振幅随着时间的增加会越来越大，导致系统失稳，从而产生噪声。

2 有限元模型

以某车型盘式制动器为数学模型，通过Abaqus软件建立有限元模型。为保证计算的精度和收敛，对有接触的区域采用高质量的单元类型，制动盘和摩擦片采用六面体和五面体单元。制动钳和制动鼓采用四面体单元。

由于摩擦片有一部分为各向异性的耐磨材料，一部分为一般的金属材料，在两部分连接区域的节点分布保持一致，通过节点合并，使二者连接在一起。制动钳和摩擦片之间通过tie绑定约束，在摩擦片和制动盘之间建立类型为Contact Pair的接触。整个模型有12万个单元，5.7万个节点，如图1所示。

3 仿真结果与试验结果对比及分析

复模态计算得到的模态频率是复数。复频率实部体现了系统在该阶模态下的阻尼特性，虚部反映了该阶振型的固有频率。如果某阶复频率的实部为正值，则说明该阶模态的阻尼比为负数，在振动过程中，随着时间增加其振幅会越来越大，导致系统不稳定，这样的模态就是不稳定模态。由于计算模型没有考虑材料的阻尼，因此计算出来的不稳定模态数会比实际要多，一般将阻尼比小于-0.01的不稳定模态才作为会产生制动噪声的不稳定模态[4]。

根据该款制动器测试结果，如图2所示，在400 Hz左右出现有明显的噪声峰值。该制动噪声为moan噪声，主要为制动钳或者支架刚度不足造成的振动放大[5]。通过对制动器模型中低频段的复模态分析，得出复特征值分布，如图3所示，出现3个不稳定模态，在407.59 Hz模态的阻尼比为-0.058 4，2 145.7 Hz模态的阻尼比为-0.035 3，2 463.6 Hz模态的阻尼比为-0.018 1。第一个不稳定模态正好和测试结果吻合，说明建立的复模态分析模型比较准确。

这3个不稳定模态的振型如图4所示，从振型图也可看出

这3个不稳定模态均是由于制动钳体刚度不足在制动过程中产生剧烈振动导致的。可以通过改进制动钳体结构、提高钳体刚度来改善中低频段的制动噪声。

图5为改进前后制动钳结构对比，对新的制动钳体建立有限元模型，通过复模态分析，3 000 Hz频率以下没有出现不稳定模态，如图6所示。

对于制动器高频制动尖叫噪声(5～20 kHz)，可以建立简化的制动器模型，略去制动钳体结构和制动鼓，以提高模型计算效率。简化的有限元模型如图7所示。

对制动盘和摩擦片组成的模型进行复模态分析，如图8所示,有3个不稳定模态，分别为：5 100 Hz，阻尼比为-0.013 54；10 049 Hz，阻尼比为-0.018 02；11 535 Hz，阻尼比为-0.015 55。还有其他一些负阻尼比的模态，但是负阻尼比均大于-0.01，在实际有阻尼的情况下，这些不稳定模态出现的概率很低。图9为3个不稳定模态的振型图。

对于高频尖叫噪声，影响因素有摩擦因数、制动盘刚度、摩擦片背板刚度以及摩擦片形状[5]。降低摩擦因数、制动盘刚度以及摩擦片背板刚度都有利于使制动系统稳定，但是会对制动性能影响较大，这里主要从改进摩擦片形状来提高制动系统稳定性。图10为优化前后的摩擦片结构对比，优化后采用两边带30°斜角、中间带缝隙的摩擦片结构。

对优化后的结构进行复模态分析，复特征值分布如图11所示，在15～20 kHz之间还有几个不稳定模态，但是负阻尼比均大于-0.01，负阻尼比小于-0.01的不稳定模态都已消除。优化后的摩擦片结构能明显提高制动系统的稳定性。

4 结论

通过分析制动噪声的产生机制，建立了某款有制动噪声的盘式制动器有限元模型，通过复模态结果分析得出以下结论：

(1)利用Abaqus软件的接触摩擦功能，建立了带摩擦耦合的制动器有限元模型，通过分析复模态特征值分布和相应振型，并与制动器噪声测试结果对比，结果表明建立的摩擦耦合的有限元模型能够较好地预测制动器实际发生制动噪声的现象。

(2)低频段的moan噪声一般是由于制动钳结构刚度不足引起的，复模态分析结果也验证了这点。通过改进制动钳结构，提高结构刚度，能有效消除低频段的制动噪声。

(3)对于高频段的制动尖叫噪声，改进了摩擦片的结构，采用了两边带30°斜角、中间带缝隙的摩擦片结构，也能提高系统的稳定性，消除制动噪声。

【1】KUSANO M.Experimental study on the reduction of drum brake noise[R].SAE851465,1985.

【2】KINKAID N M,O’REILLY O M,PAPADOPOULOS P.Automotive Disc Brake Squeal[J].Journal of Sound and Vibration,2003,267(1):105-166.

【3】王登峰,王玉为,黄海涛,等.盘式制动器制动尖叫的有限元分析与试验[J].汽车工程,2007(8):705-709.

【4】侯俊,过学迅.基于有限元方法的盘式制动器制动噪声研究[J].机械设计,2008,25(8)：50-52.

【5】郭鸣.盘式制动器非线性振动与尖叫问题的模态分析与研究[D].武汉：武汉理工大学，2010.

Optimization and Analysis for Brake Noise of a Car Disc Brake

FU Guang, LIANG Jingqiang, LIU Zhongwei, LV Juncheng

(SAIC GM Wuling Automobile Co.,Ltd.,Liuzhou Guangxi 545007,China)

The FEA model of a disc brake was set up with the combination of complex mode analysis theory and FEM in Abaqus software. Complex modes under 20 kHz were calculated, and the unstability of brake system could be recognized by the positive real part of complex eigenvalue, the unstability would cause brake noise. The calculation results matched with the test results, it was indicated FEA model was correct. The new structures of brake bracket and friction disc were given. The new FEA results indicate that new structures can make the brake system more stable.

Disc brake; Brake noise; Complex mode analysis; Finite element

2015-07-13

付广，男，硕士，研究方向为整车NVH仿真分析及测试。E-mail：fug2008@163.com。