结构面参数对顺层边坡破坏模式的影响规律

黄 帅 王 荣 汪洪祥 蔡德钩 闫宏业

(1.中国地震局地壳应力研究所，北京 100085;2.中国港湾工程有限责任公司，北京 100027;3.中国铁道科学研究院铁道建筑研究所，北京 100081)

·安全与环保·

结构面参数对顺层边坡破坏模式的影响规律

黄 帅1王 荣2汪洪祥2蔡德钩3闫宏业3

(1.中国地震局地壳应力研究所，北京 100085;2.中国港湾工程有限责任公司，北京 100027;3.中国铁道科学研究院铁道建筑研究所，北京 100081)

基于岩质顺层边坡的离散元仿真模型，研究了结构面各参数(黏聚力、内摩擦角、刚度、倾角、间距)对边坡稳定性的影响，明确了其对边坡安全系数及破坏模式的影响规律。采用正交试验的极差分析原理，探讨了各结构面参数对边坡稳定性影响的显著程度，明确了结构面各因素对边坡安全系数影响的显著顺序。研究表明，随着结构面强度的增大，边坡安全系数在一定范围内呈线性增长，且边坡的破坏模式从顺层滑移逐渐转变为滑移-弯曲破坏模式；随着结构面刚度和结构面间距的增加安全系数变化幅度很小，其最大变化率仅为6.6%和3.6%，边坡破坏模式主要为滑移式破坏。随着结构面倾角的增大边坡安全系数表现为减小—增大—减小的趋势，破坏模式由滑移式破坏变为滑移-溃曲破坏最后变为倾倒破坏；结构面黏聚力对边坡稳定性影响最大，结构面刚度影响最小。

顺层边坡 结构面 正交试验 安全系数 破坏模式

滑坡危害范围广，难以预测，其一旦发生就会造成较大的生命财产损失，一直以来都是地质灾害领域研究的重点。而顺层边坡是岩石边坡中研究的一个重点和难点[1]，是山区铁路和公路建设中常见的工程问题。例如，2003年建成的重庆万梁高速公路岩质路堑高边坡有115个，其中顺层边坡的个数为所有边坡的52%。2005年建成的渝怀铁路全长约为600 km，全线顺层路基累计长约40 km，占路线长度的6.7%[2]。此外，据统计[3]顺层边坡常年事故频发，严重影响工程建设。

顺层边坡的破坏与失稳是岩土工程重大灾害之一，其在自重引起的滑移力作用下受到结构面、坡角、岩层走向等因素的影响，不同的因素对其稳定性影响不同，而结构面参数是其主控因素。国内外对顺层边坡的稳定性进行了较多的研究。Hatzor等[4]研究了动力载荷对边坡稳定性的影响。林杭等[5]研究了结构面倾角对边坡稳定性的影响规律。卢敦华等[6]研究了安全系数随黏聚力和内摩擦角的变化规律。魏俊奇等[7]研究了结构面间距对边坡破坏模式的影响规律。陈从新等[8]研究了坡形对边坡稳定性的影响规律。路为等[9]研究了岩质顺层边坡的平面滑移破坏机制。冯君等[10]研究了结构面倾角和强度参数对边坡稳定性的影响规律。然而，尽管对顺层边坡的稳定性进行了较多研究，但是大多是针对单一因素以及结构面的某类参数进行了分析，并没有给出较为全面的结构面参数对边坡稳定性的影响，且很少涉及结构面各参数对边坡稳定性影响的敏感性研究。此外，由于结构面对岩体的分割使得岩体结构变成非均质、各向异性、非连续的三相介质，确定滑动面是比较困难的，且传统的极限平衡法难以应用于顺层边坡。因此，本研究基于离散单元法，分析结构面参数对顺层边坡破坏模式的影响规律。

1 结构面各参数对边坡破坏模式影响分析

1.1 离散元数值仿真模型

本研究以顺层岩质边坡为研究对象，坡高H为40 m，坡角为45°，模型长200 m(5H)，模型高80 m(2H)，坡脚前缘岩体宽度取100 m(2.5H)，模型高度取80 m(2H)。边坡底部为固定约束边界条件，左右两侧为水平位移约束条件，其他面为自由边界，计算模型如图1所示，边坡岩体计算参数如表1所示。重点分析岩体结构面对边坡稳定性的影响，因此结构面各参数(结构面间距、倾角、法向刚度、切向刚度、内聚力和摩擦角)作为变量处理。

图1 边坡的计算模型(单位：m)

泊松比密 度/(kg/m3)体积模量/GPa剪切模量/GPa黏聚力/MPa内摩擦角/(°)抗拉强度/MPa0325501426540142921

1.2 结构面参数对边坡破坏模式的影响分析

为了研究结构面参数对顺层边坡稳定性的影响，分别变化结构面各参数，具体计算方案设计如表2所示。

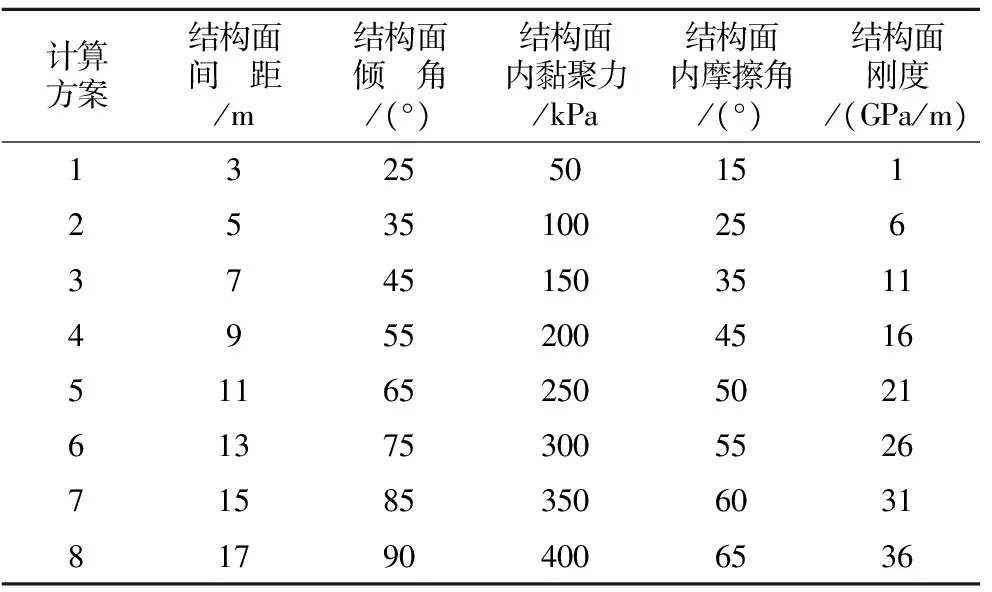
表2 计算方案

通过数值仿真分析，可得结构面2个因素对边坡的安全系数影响规律如图2所示。

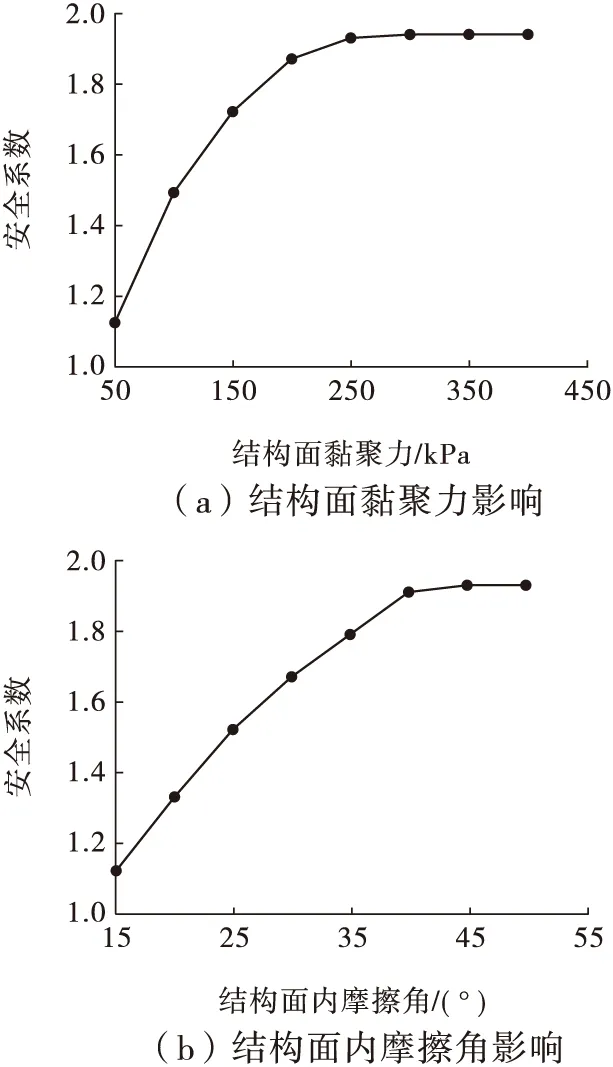
图2 结构面强度参数对边坡安全系数的影响

由图2(a)和图2(b)发现：当结构面强度参数值小于边坡岩体强度参数值时，随着结构面强度参数的增加，边坡安全系数呈线性增长；当结构面强度参数值超过边坡岩体强度参数值后，随着强度参数值的增加，安全系数的增幅逐渐减小。当结构面黏聚力超过边坡岩体黏聚力的1.78倍时边坡安全系数呈现不变的趋势；结构面摩擦角超过边坡岩体内摩擦角的1.4倍时，安全系数基本保持不变。分析其原因为：当结构面强度参数值小于岩体强度参数值时，边坡的破坏受控于结构面强度参数，从而呈现出线性关系；当结构面强度参数值超过岩体强度一定值时边坡的破坏受控于边坡岩体强度参数，从而随着结构面强度参数的增加呈现不变的趋势。

由于坡体在滑动失稳时滑动面两侧岩土体的速度矢量场存在不连续变化的特征，因此可以根据失稳破坏时坡体的速度矢量场来确定潜在滑动面的位置[11]。基于此，为了确结构面强度参数对边坡破坏模式的影响，提取了结构面强度参数变化时边坡的速度矢量图，如图3和图4所示。

图3 结构面不同黏聚力对边坡破坏模式的影响

图4 结构面内摩擦角对边坡破坏模式的影响

当结构面黏聚力小于边坡岩体的黏聚力时，边坡的破坏模式为顺层滑移破坏模式如图3(a)、图3(b)；当结构面的黏聚力和内摩擦角大小超过边坡岩体的黏聚力和内摩擦角时，破坏模式从顺层滑移逐渐转变为滑移-弯曲破坏模式，滑移面由平面转化为圆弧面，如图3(d)～图3(h)，且当边坡的破坏模式的转变均开始于结构面黏聚力和内摩擦角与边坡岩体黏聚力和内摩擦角相等时，如图3(c)，进一步验证了研究计算的结构面黏聚力对边坡安全系数影响规律的准确性。

由图4可以看出：随着结构面内摩擦角的增大，边坡的破坏模式与结构面黏聚力增大时边坡的破坏模式表现出相同的变化规律。即当结构面内摩擦角小于边坡岩体的内摩擦角时，边坡的破坏模式主要为顺层滑移破坏模式如图4(a)～图4(c)；当结构面的黏聚力超过边坡岩体的内摩擦角时，破坏模式从顺层滑移逐渐转变为滑移-弯曲破坏模式，滑移面由直线型转化为圆弧形，如图4(e)～图4(h)，且边坡的破坏模式的转变均开始于结构面内摩擦角与边坡岩体内摩擦角相等时，如图4(d)。

由图5可知：随着结构面刚度和结构面间距的增加安全系数变化幅度很小，其最大变化率分别为6.6%和3.6%，这说明变形参数和结构面间距对于边坡稳定性的影响有限。当结构面倾角小于坡角时，随着结构面倾角的增大边坡安全系数有减小的趋势；当结构面倾角大于坡脚时，随着结构面倾角的增大，安全系数呈现增大的趋势，直到结构面倾角达到75°时达到最大值1.69，之后随着结构面倾角的增大边坡的安全系数又出现减小的趋势。说明在结构面倾角小于坡脚时随着结构面倾角的增大，滑块在重力作用下的下滑力增大，导致边坡安全系数的减小，当结构面倾角大于坡脚一定角度时边坡的破坏主要是由于边坡岩体的弯折破坏导致。当结构面倾角超过边坡坡脚某一角度时(本文为75°)由于边坡岩体在重力作用下极易出现倾倒破坏，从而导致边坡安全系数的减小。

图6、图7和图8揭示了结构面刚度、结构面间距及结构面倾角对边坡破坏模式的影响。

由图6可以看出，在顺层边坡中，当结构面刚度不断增大时，边坡受到自重引起的顺层滑移力作用，破坏模式主要表现为沿着层面顺层滑动破坏。

由图7可以看出，在顺层边坡中，当结构面间距不断增大时，边坡主要受到自重引起的顺层滑移力作用，其破坏模式并没有发生变化，依然表现为沿着层面滑动破坏。因此，结构面间距变化对边坡破坏模式影响较小。

图5 结构面刚度、结构面间距及结构面倾角对边坡安全系数的影响规律

图6 结构面刚度对边坡破坏模式的影响

图7 结构面间距对边坡破坏模式的影响

图8 结构面倾角对边坡破坏模式的影响

由图8可以看出：当结构面倾角小于边坡坡脚时边坡的破坏表现为楔形滑动破坏，图8(a)、图8(b)；当结构面倾角大于边坡坡脚时，发现坡脚处易产生应力集中现象，岩体出现屈服，变形较大，边坡的破坏模式由顺层滑动转变为滑移-溃曲破坏，如图8(c)～图8(f)所示；直到结构面倾角达到85°边坡的破坏模式开始由滑移-溃曲破坏逐步向倾倒破坏模式转变如图8(g)～图8(h)所示。这进一步验证了本研究中结构面倾角对边坡安全系数影响规律的准确性。

2 边坡稳定性参数的敏感性分析

对边坡而言，结构面各参数对其稳定性能影响的显著性不同，有必要确定各参数对顺层边坡稳定性影响的敏感性大小。在实际问题中，考虑1个因素或2个以上因素对计算结果的显著性分析可以选用一元或二元方差分析，而研究顺层边坡的稳定性需考虑多个因素对其稳定性的影响，可采用正交试验的方法进行分析[12]。

为了明确结构面各参数对边坡稳定性影响的显著性，采用正交试验进行数值分析，研究结构面间距(A)、结构面倾角(B)、结构面黏聚力(C)、结构面内摩擦角(D)、结构面刚度(E)对边坡的稳定性的影响规律，即以边坡稳定安全系数为指标进行多因素单指标计算分析。不考虑各因素的交互作用,即假定它们之间相互没有影响。本次试验采用5因素4水平正交分析,即每个影响因素有4个可选取的值进行研究如表3所示，并至少要进行16次试验,即为L16(45)正交表进行试验，试验见表3。

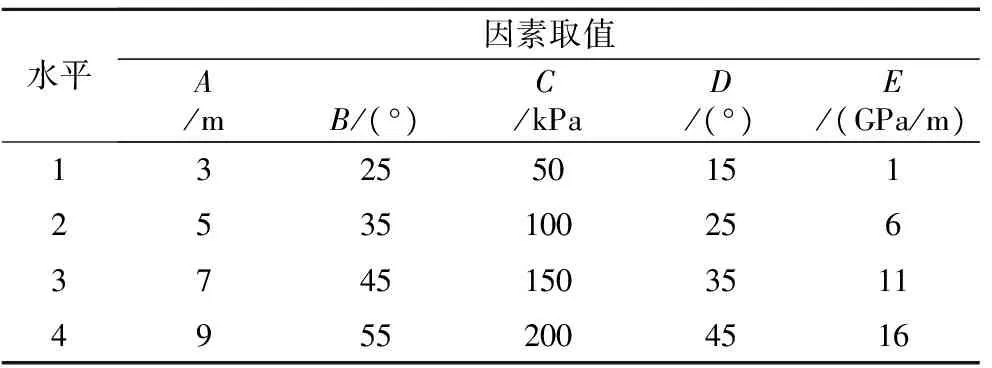
表3 不同水平下各因素取值

表4 正交试验结果

通过数值分析求出各因素不同水平下边坡安全系数的均值，并对其进行极差分析如图9和图10所示。

图9中横坐标为各因素的水平，纵坐标反映安全系数Fs在各因素不同水平下的平均值。分析发现：边坡的安全系数随着结构面黏聚力、内摩擦角、结构面倾角的增大均表现出增大的趋势，其中结构面的黏聚力和内摩擦角对安全系数的影响最大，结构面倾角对边坡安全系数的影响比较小。而边坡安全系数随着结构面刚度和结构面间距增加到一定值时，出现减小的趋势，与前文得出的结论相同。边坡安全系数计算值最大时的方案为A2B4C4D3E3，即在此方案下边坡的安全系数最大，此时边坡最稳定。边坡安全系数计算值最小时的方案为A1B1C1D1E1，即在此方案下边坡的稳定性最差。

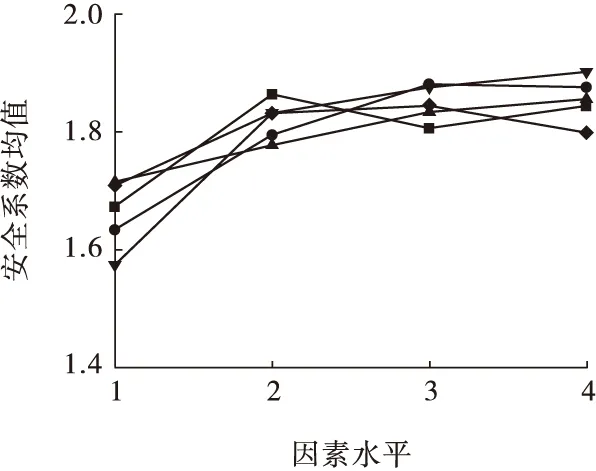
图9 各因素不同水平下安全系数均值

图10 各因素对应安全系数极差

由图10可知，安全系数极差从大到小的顺序依次为RC、RD、RA、RB、RE，表明在考虑的结构各参数中结构面黏聚力对边坡稳定性影响最大，其次为结构面摩擦角、结构面间距、结构面倾角、结构面刚度，其中结构面倾角和结构面刚度对边坡稳定性系数的影响程度相差不大。

3 结 论

(1)当结构面强度参数(黏聚力和内摩擦角)小于边坡岩体强度参数时，随着结构面强度增加，安全系数近于线性增加，破坏模式以顺层滑移破坏模式为主；当结构面参数大于边坡岩体强度参数时，随着结构面强度的增加，边坡安全系数逐渐趋于定值，破坏模式由顺层滑移变为滑移-弯曲破坏，且滑移面由平面变为圆弧面。

(2)结构面刚度和结构面间距对安全系数的影响较小，且随着结构面刚度和间距的增大，边坡破坏模式主要表现为沿着结构面顺层滑动破坏。

(3)当结构面倾角小于坡角时，随着结构面倾角的增大，边坡安全系数有减小的趋势，主要以顺层滑移破坏为主；当结构面倾角大于坡角且小于某一临界角度值时，随着结构面倾角的增大，安全系数呈现增大的趋势，主要以滑移-溃曲破坏为主；直到结构面倾角超过临界值之后，随着结构面倾角的增大边坡的安全系数又出现减小的趋势，且破坏模式转变为倾倒破坏。

(4)基于正交试验获取了结构面不同因素对边坡稳定性影响的主次顺序，得出岩体结构面黏聚力对岩质边坡的稳定性影响最大，其次是结构面内摩擦角、结构面倾角、结构面间距和结构面刚度。

[1] Friedkin J F.Alaboratorystudyof Themeandering of Alluvial River[R].[S.l.]:US Water ExpSta，1945:225-271.

[2] 李安洪，周德培，冯 君，等.顺层岩质边坡稳定性分析与支挡防护设计[M].北京:人民交通出版社,2011. Li Anhong，Zhou Depei，Feng Jun,et al.Assistant Designed and Stability Analysis of Rock Mass Bedding Slope[M].Beijing:China Communications Press，2011.

[3] 李云鹏，杨治林，王芝银.顺层边坡岩体结构稳定性位移理论[J].岩石力学与工程学报，2000，19(6):747-750. Li Yunpeng，Yang Zhilin，Wang Zhiyin.Displacement analysis of structure stability for rock massbedding slope[J].Chinese Journal of Rock Mechanicsand Engineering，2000，19(6):747-750.

[4] Hatzor Y H，Arzib A A，Zaslavskyc Y，et al.Dynamic stability analysis of jointed rock slopes using the DDA method[J].International Journal of Rock Mechanics & Mining Sciences，2004,41:813-832.

[5] 林 杭，曹 平,等.层状岩质边坡破坏模式及稳定性的数值分析[J].岩土力学，2010,31(10):3301-3304. Lin Hang，Cao Ping,et al.Numerical analysis of failure modes and stability of stratified rock slopes[J].Rock and Soil Mechanics,2010，31(10):3301-3304.

[6] 卢敦华,曲艳伟,等.结构面强度参数对层状边坡稳定性影响的三维分析[J].中南大学学报:自然科学版,2011,42(1):147-150. Lu Dunhua，Qu Yanwei,et al.Three dimensional analysis for effect of structural plane strength parameters on stratified slope stability [J].Journal of Central South University:Science and Technology,2011,42(1):147-150.

[7] 魏俊奇,王礼珍,王 丽.顺层岩质边坡稳定性分析与应力监测研究[J].水利与建筑工程学报,2011,9(6):44-47. Wei Junqi，Wang Lizhen,Wang Li.Study on stability analysis and stress monitoring of bedded rock slope[J].Journal of Water Resources and Architectural Engineering,2011,9(6):44-47.

[8] 陈从新，黄平路，卢增木.岩层倾角影响顺层岩石边坡稳定性的模型试验研究[J].岩土力学,2007，28(3):476-481. Chen Congxin，Huang Pinglu，Lu Zengmu.Study on correlation between stability of consequent rock slope and obliquity of rock layer by simulation experiment[J].Rock and Soil Mechanics,2007,28(3):476-481.

[9] 路 为，白 冰，陈从新.岩质顺层边坡的平面滑移破坏机制分析[J].岩土力学,2011,32(S2):204-207. Lu Wei，Bai Bing，Chen Congxin.Analysis of mechanism of plane sliding failure for bedded rock slopes[J].Rock and Soil Mechanics，2011,32(S2):204-207.

[10] 冯 君,周德培,李安洪.顺层岩质边坡开挖模型试验及稳定性影响因素分析[J].工程地质学报,2005,13(3):294-299. Fen Jun，Zhou Depei，Li Anhong.Test and numerical modeling of the stability of rock bedded slope[J].Journal of Engineering Geology，2005,13(3):294-299.

[11] 李海波，肖克强,刘亚群.地震荷载作用下顺层岩质边坡安全系数分析[J].岩石力学与工程学报,2007,26(12):2386-2392. Li Haibo，Xiao Keqiang，Liu Yaqun.Factor of safety analysis of bedding rock slope under seismic load[J].Chinese Journal of Rock Mechanics and Engineering，2007,26(12):2386-2392.

[12] 付宏渊，刘建华，张 立，等.基于正交试验的岩质边坡动力稳定性分析[J].中南大学学报:自然科学版,2011,42(9):2853-2859. Fu Hongyuan，Liu Jianhua，Zhang Li，et al.Dynamic stability analysis for rock slope based on orthogonal test[J].Journal of Central South University:Science and Technology,2011,42(9):2853-2859.

(责任编辑 石海林)

Study on Influence Laws of Rock Structural Plane Parameters on Failure Mode of Bedding Slope

Huang Shuai1Wang Rong2Wang Hongxiang2Cai Degou3Yan Hongye3

(1.InstituteofCrustalDynamics，ChinaEarthquakeAdministration，Beijing100085，China；2.ChinaHarbourEngineeringCompanyLimited，Beijing100027，China；3.RailwayEngineeringResearchInstitute，ChinaAcademyofRailsScience，Beijing100081，China)

Based on the discrete element numerical simulation of rock slope，influences of the parameters (cohesion，internal friction angle，rigidity，dip angle，spacing) of rock structural plane to slope stability is studied to clear the influencing law for safety factor and failure modes of slope.According to the principle of variance analysis of orthogonal experiment，the significance that rock structural plane parameters impact on the slope stability is discussed.It is shown that slope safety factor is on linear growth in a certain range with strength of the rock structural plane increasing，and the failure modes shift gradually from the bedding sliding failure modes to the sliding-bending failure modes.The safety factors changes very little with the rigidity and spacing of rock structural plane increasing.Its maximum variance ratio is only 6.6% and 3.6%，and the slope failure modes are mainly sliding failure modes.Slope safety factor firstly decreases，then increases and finally decreases with the increase of the rock structural plane dip angle，and failure modes shift from shearing slip failure modes to shearing slip-buckling failure modes，finally to the tilting failure modes.The impact of the rock structural plane cohesion on the slope stability is the greatest，and the rigidity is the least.

Bedding slope，Rock structural plane，Orthogonal experiment，Safety factor，Failure mode

2015-06-22

国家高技术研究发展计划(863计划)项目(编号：2011AA11A102),铁道科学技术研究发展中心科研项目(编号：J2014G006)。

黄 帅(1987—)，男，助理研究员，博士。

U211.9

A

1001-1250(2015)-10-140-06