精确毫秒延时控制爆破地震反应谱特性研究

何 理 钟冬望 涂圣武 操 鹏

(武汉科技大学理学院，湖北 武汉 430065)

精确毫秒延时控制爆破地震反应谱特性研究

何 理 钟冬望 涂圣武 操 鹏

(武汉科技大学理学院，湖北 武汉 430065)

利用地震工程中应用较为成熟的反应谱理论对精确毫秒延时控制爆破地震进行研究，设计开展了边坡爆破开挖相似模型试验，分析了不同毫秒延时对爆破地震反应谱特性的影响，考虑结构密集振型间相互影响，结合完全二次项组合法(CQC)求得结构反应总效应值。结果表明：短毫秒延时控制爆破地震反应谱曲线体现为多峰值特性，且峰值对应周期范围窄，通常在几毫秒区间内；随孔间毫秒微差的增加，反应谱峰值对应结构自振频率逐渐降低，愈趋接近构筑物自振频率，不利于构筑物安全；合理孔间延期时间选取时，应综合考虑爆破振动强度、岩体爆破效果和构筑物动力效应特性3个方面因素；试验条件下，合理孔间延期时间为2 ms。

边坡 爆破振动 反应谱 模态组合 CQC法 延期时间

有效防治爆破振动危害是岩土爆破、矿山开采、地下开挖及水下石油开采等爆破工程中亟待解决的工程难题之一。目前，采用单一的爆破振动速度作为构筑物安全评价指标的独立阈值理论愈来愈满足不了实际需要，此法虽然简便，但局限性较大。例如实际爆破工程中，相同爆破条件下，爆心距远的构筑物反而先于爆心距近的构筑物破坏，抑或同一构筑物，不同部位的损伤、破坏情况却不尽相同。主要是因为基于单一爆破地震动强度的经验判据法未充分考虑结构本身固有动力特性、材料性能以及自由度条件与爆破地震波特性的综合作用影响。目前，地震反应谱分析理论被广泛应用于结构在爆破振动作用下的动力响应分析研究，并取得良好效果[1-4]。在爆破地震反应谱研究方面，李夕兵、凌同华等[5-6]研究了不同段药量、爆心距及段数的爆破地震反应谱特性；荣立爽、孙建生[7]研究了水下岩塞爆破反应谱的结构响应及影响因素；唐鸿卿、吴新霞[8]研究了振动频率对结构反应谱的影响；李洪涛等[9]研究了地下隧道开挖爆破的地震反应谱特征；娄建武[10]、孙新建[11]、包辉等[12]提出采用反应谱曲线积分值来评估爆破振动危害效应；丁刚德[13]、王凯等[14]研究了不同微差时间下微差爆破振动的反应谱特征。高精度数码电子雷管的精确毫秒延时控制爆破技术不仅能有效降低爆破振动强度，且能改善岩石爆破效果，因此被广泛应用于各类爆破工程[15-19]。但针对精确毫秒延时控制爆破的地震反应谱特性研究还鲜有报道，且前人基于地震反应谱分析对结构物进行稳定性评价时，很少考虑结构不同阶振型对结构反应总效应的贡献差异，多数采取其反应谱峰值作为评判指标。基于此，结合室内相似模型试验，对精确毫秒延时控制爆破振动信号进行地震反应谱研究，分析毫秒延期时间对结构反应谱特性的影响，考虑各阶振型间相互影响关系，探讨合理孔间延期时间选取原则，以期进一步完善毫秒延时爆破理论及其效应。

1 结构地震反应模态组合理论

1.1 反应谱理论

反应谱分析是黏性阻尼体系在地震动作用下的结构动力学响应分析，相应的反应谱曲线即地震最大反应与结构自振周期(自振频率)间的关系。地震动作用下，单自由度体系的运动方程可表示为

(1)

通过式(1)即可求得体系的最大绝对加速度、最大相对速度和最大相对位移[7-8,13-14]。

地震反应谱计算中，将体系某一最大反应与输入激励的最大反应之比值定义为放大系数，用以表征结构体系的动力响应效应，分为速度放大倍数、加速度放大倍数和位移放大倍数3种。将放大倍数与结构体系自振周期间的关系曲线称之为标准反应谱，相应的分别有标准速度反应谱、标准加速度反应谱和标准位移反应谱3种。标准反应谱图反映了结构体系对地震波中特定频率成分的选择放大作用，体现了结构体系对地震响应的动力效应[20]。

1.2 反应谱的数值计算

基于精确法计算的反应谱主张将地面运动的加速度记录相邻点间的值用分段线性插值表示，进而获得地面运动的连续表达式。获得的结果全部采用精确的分析方法，不存在任何的舍入误差，也不会产生任何截断误差，故避免了数值计算过程出现的误差，因此其具有较高精度，并且只需较少的运算次数即可达到其他方法需要较多运算才能达到的精度[21]。

1.3 结构地震反应的模态组合[22-23]

对于多自由度体系，反应谱法可计算得到各振型反应量的最大值，然而它们并非出现在同一时刻，也就是说，各阶振型反应对结构体系动力响应的贡献是不对等的。在求结构体系各阶模态反应的总效应R时，若简单地将各阶振型反应Ri叠加会使得计算结果偏于保守，此时就需要考虑振型间的相互影响关系，即地震反应的模态组合，以便使得计算出的总反应峰值更符合实际情况。

选取完全二次项组合(CQC)方法进行模态组合，CQC模态组合法通过引入振型相关系数，考虑了结构体系密集振型间的相互影响因素；并且无需考虑爆破地震动白噪声持续时间的影响，相应地避免了通常用加速度强震持时代替白噪声持时而产生的误差，且计算方法便捷，计算结果准确。结构振型反应总效应表达式为

(2)

式中，R为各阶模态反应总效应；εij为第i阶和第j阶振型相关系数，0<εij<1，且i≠j；Ri为第i阶振型反应；Rj为第j阶振型反应；n为结构体系模态阶次。

振型相关系数εij可表示为

(3)

式中，wi、wj分别为第i阶振型和第j阶振型的自振频率；ξi、ξj分别为第i阶振型和第j阶振型下阻尼比系数。

2 精确毫秒延时控制爆破试验

2.1 模型试件的制作

为保证模型试验结果具有可推广性，根据露天矿山台阶爆破生产实际爆破参数，尽量加大模型边界尺寸，选取合适的几何缩比。一般露天矿山台阶爆破中，台阶高度H=10～15 m，最小抵抗线WD=4～6 m，孔径d=0.2 m，超深h1=1～2 m，堵塞长度h0=4～6 m，孔距a=7～10 m，排距b=4～6 m，坡角φ=70°。选取几何缩比k=1∶50。混凝土边坡模型尺寸：台阶高度H′=350 mm，孔径d′=10 mm，孔距a′=150 mm，排距b′=90 mm，堵塞长度h0′=(80～120) mm，坡角φ′=70°。模型尺寸如图1所示，单位为mm。

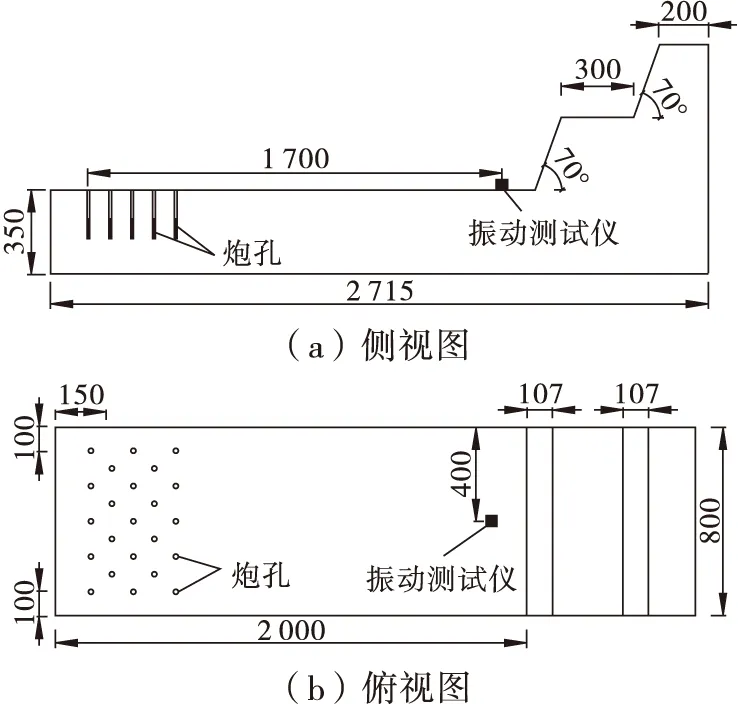
图1 模型尺寸

为改善模型边界条件的相似性，减小爆破试验的边界效应，本试验模型浇注前在地面挖长×宽×高尺寸为2.72 m×0.8 m×0.35 m的长方体土坑作为边坡梯段爆破开挖时坡底部分的模具(见图2(a))。挖坑时尽量使得土坑四壁及坑底呈波浪形状，以削弱反射波的叠加作用。同时，待试件浇注完成直至硬化后，用打夯机将模型四周岩土夯实，使得混凝土模型与坑周围土体紧密结合，以增加应力波的透射，减小反射，尽可能降低反射波对台阶上表面爆破地震波的影响。模型浇注完成后如图2(b)所示。

图2 模型实物图

模型试件的制作采用325#硅酸盐水泥和筛选后的细砂浇注而成，确定其配比为0.44∶1∶2.5(水、水泥、砂子的质量比)，在制作模型时同时浇注3个150 mm×150 mm×150 mm的标准混凝土试样，用以测试模型力学参数，模型和标准试样制作完成后，用草帘遮盖，定时洒水养护28 d，以达到预期强度。测得养护完成后的标准试样的力学参数见表1。

表1 模型材料力学参数

在模型试件浇注过程中使用直径为10 mm的钢筋作为炮孔预埋件(见图2(b))，炮孔采用梅花形布置，试件浇注完成后，定时(每隔1～2 h)轻轻转动钢筋，直至模型试件硬化，拔出预埋件形成所需炮孔。

2.2 延期时间设置及振动信号获取

为模拟台阶爆破临空面，爆破试验前在坡底爆区靠外侧挖取宽约30 cm的深沟 (见图2(b))，减小夹制，利于岩体破碎以及增加用于抛掷岩石耗费的能量，从而改善边坡稳定性。

单孔装药量为2.0 g，由数码电子雷管引爆。试验过程中，振动监测点布置在各排炮孔连线中垂线上，且距离爆区最后排炮孔1.7 m处(图1(a))。

为减少爆破试验次数及人员警戒次数，采用各排孔连续起爆方式，在图1(b)的爆破区域中，从左向右孔间延期时间依次选用1、2、3、4、5 ms，排间采用等时延期时间间隔60 ms，段间延期雷管选用湖北卫东机械厂自主研发的隆芯1号数码电子雷管，其延时误差为延期设计值的1%，能保证设计延期与实际延期高度一致[17-18]。

试验测得精确毫秒延时控制爆破振动速度信号如图3所示。

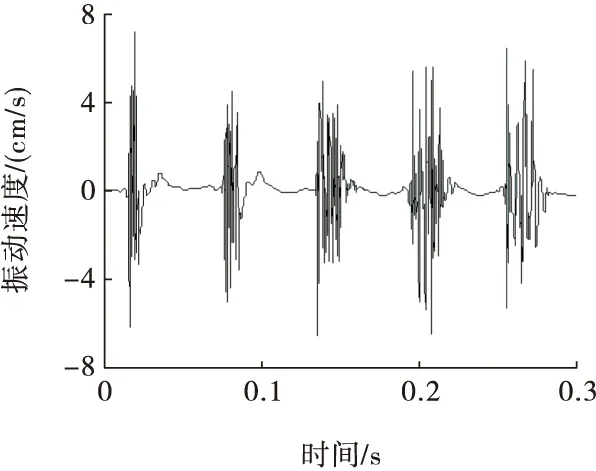
图3 振动速度信号

3 计算结果及分析

3.1 加速度信号获取及去噪

通过对试验过程中爆破振动监测得到的振动速度信号进行数值微分处理，即可得到反应谱计算时需要的加速度输入信号。数值微分计算式为

(4)

为尽可能避免数值微分过程中随机误差的影响，采用4点向前差分计算[24]：

(5)

利用式(5)进行数值微分计算加速度时，振动速度信号中微弱的趋势项会导致加速度产生很大的噪声干扰成分，使得加速度值出现高频振荡，引起加速度信号的严重失真，从而影响反应谱的计算精度，因此需要对直接微分得到的加速度信号进行小波包去噪处理[17，20]。

由于进行反应谱计算时，不同毫秒延期时间下的加速度是作为单独信号输入的，故将图3中振动速度信号根据延期时间不同分成5段，各段速度信号对应延期时间依次为1、2、3、4、5 ms，每段时长60 ms，分别对各个信号进行数值微分及小波包去噪处理，得到图4所示振动加速度信号。

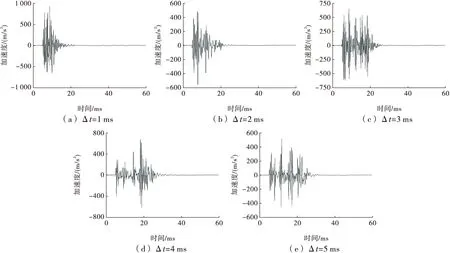
图4 加速度信号

3.2 结构地震反应谱特性分析

选取结构振动阻尼比系数ξ=0.05[19-20]，通过matlab编制计算程序，采用精确法，将图4所示加速度信号作为输入信号进行反应谱计算。由于振动速度与能量相关性高，能较好体现结构系统黏性阻尼力响应，故选取速度反应谱和标准速度反应谱为对象，对不同毫秒延时控制的爆破地震反应谱特性进行分析。不同毫秒延时控制的速度反应谱见图5，标准速度反应谱见图6。

图5 速度反应谱

由图5及图6可以看出，相同延期时间下速度反应谱与标准速度反应谱的曲线相似度较高，但反应谱各峰值大小以及突峰数量均相差较大；且随着孔间延期时间的增加，速度反应谱与标准速度反应谱的峰值个数有略微增加的趋势，相较于其他延期时间，5 ms延期情况下反应谱峰值个数最多，且曲线形态最为复杂，构筑物选择放大的几率最大，显然不利于构筑物的安全。

图6 标准速度反应谱

图5中速度反应谱峰值由大到小依次对应延期1、2、3、4、5 ms，图6中标准速度反应谱峰值依次对应延期2、3、1、4、5 ms，而输入信号加速度峰值依次对应延期1、3、4、5、2 ms。分析其原因，主要由于标准速度反应谱主要取决于结构自身固有特性，而不受输入的加速度峰值影响，体现了结构体系对不同输入信号的选择放大效应，速度反应谱则是输入信号峰值与结构自身固有属性综合作用的结果。

图5中速度反应谱峰值对应自振周期由延期3、1、2、4、5 ms逐渐增大，图6中标准速度反应谱峰值对应自振周期由延期1、3、2、4、5 ms逐渐增大，表明随孔间延期时间的增加，反应谱峰值对应的自振频率越低，越接近构筑物自振频率，产生共振可能性越大，越不利于构筑物安全。

试验条件下，段药量小，孔间延期值设置比较短，且爆心距小，导致反应谱输入信号呈现高频、短周期特性；相应反应谱曲线表现为多峰、紧密，速度反应谱和标准速度反应谱有明显放大效应所对应的周期范围非常窄，只有几毫秒。

3.3 结构模态分析

为考虑结构各阶振型间相互影响关系，通过有限元软件ANSYS对边坡结构进行模态分析。应用子空间迭代法进行求解，求出边坡结构前20阶振型，模态分析的最高阶频率已达到400.1 Hz，大于加速度输入信号的频率范围上限值。边坡结构的固有频率和振型如表2所示。

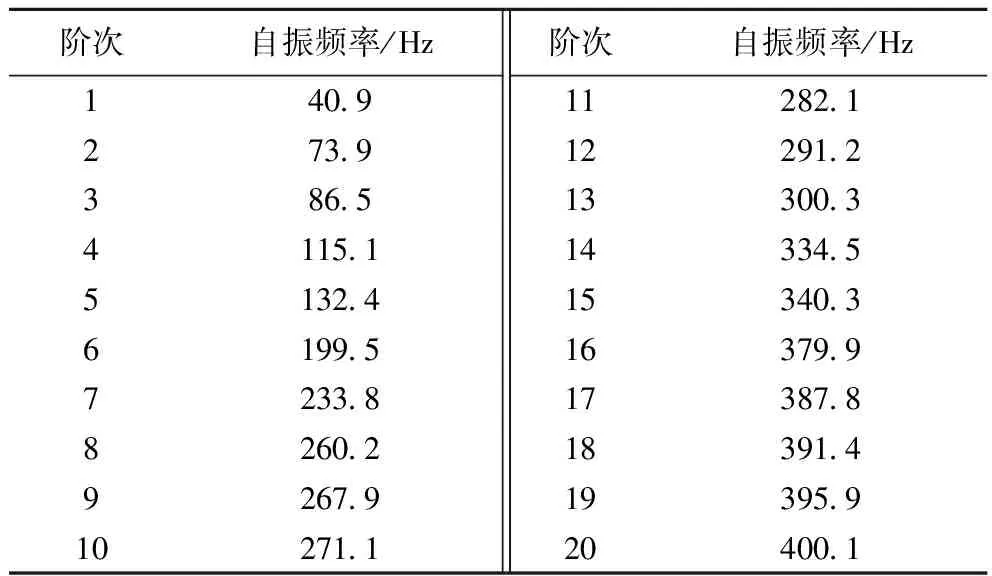
表2 模态分析结果

3.4 振型相关系数求解

选取各阶振型阻尼比系数为0.05[19]，根据表2中各阶振型自振频率，通过式(3)计算出各振型间相关系数，共计380个计算值。若将第i阶与第i+1阶振型间相关系数定义为相邻振型相关系数(i=1，2，3，…，19)，将第1阶分别与第2、3、4，…，20阶振型间相关系数定义为渐远振型相关系数，则相邻振型相关系数与渐远振型相关系数随计算阶次的关系如图7所示。

图7 振型相关系数

由图7可以看出，相邻振型相关系数随着计算阶次的增加，呈现升降交替的趋势变化，但总体上仍然呈现逐级增加趋势，主要是因为边坡结构模态随阶次的增加，其自振周期分布逐渐变得密集，从而导致耦合振型间相互影响作用增强，这也是本研究选取CQC模态组合法计算结构反应总效应的主要原因。渐远振型相关系数随计算阶次的增加，初期呈现指数型衰减趋势，随后呈缓慢衰减，最后趋于稳定。这里定义的渐远振型相关系数最大值为0.008 5，仅仅与相邻振型相关系数的最小值相当，表明CQC法中最能体现耦合振型间相互作用的模态阶次为相邻阶模态，且为处于输入加速度信号频域范围内的结构体系高阶模态。实际应用时，对结构体系进行模态求解应尽可能增加截断模态阶次，避免漏算高阶相邻振型相关系数。

3.5 CQC法求解地震反应总效应

根据式(2)，结合matlab 7.0编制计算程序，分别对不同毫秒延时控制的爆破振动加速度信号计算边坡结构地震反应总效应值。爆破地震反应总效应值见表3。

表3 爆破地震反应总效应

为便于比较分析，将边坡结构爆破地震反应总效应值随毫秒延时的关系示于图8。

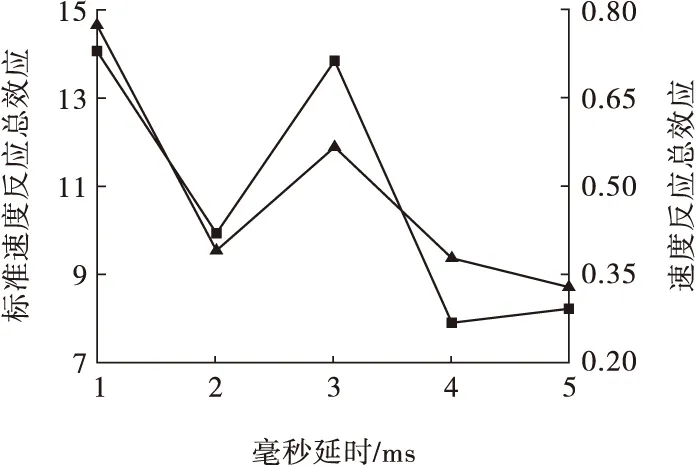
图8 地震反应总效应随毫秒延时的关系

由图8可以看出：速度反应总效应和标准速度反应总效应随毫秒延时的增加，呈现出先减小，后增大，而后又缓慢减小的趋势，并且整体呈现出逐渐减小的趋势，且均在延时2 ms时出现极小值，分别为0.39、9.9。当毫秒延时逐渐增加至4 ms时，2种反应总效应值依次为0.37、7.87，与2 ms延期情况下相当；结合图4(d)可以看出，此时各分段加速度波形已逐渐分离开来，但仍然有微弱的叠加现象存在，从岩石爆破效果角度看，显然是不利于岩石破碎的。当毫秒延时为5 ms时，2种反应总效应值依次为0.33、8.19，速度反应总效应值到达最小值，即此时加速度输入信号对边坡结构动力破坏效应最小；但由图4(e)可以得到，此时各分段震波几乎分离开，叠加现象几近消失。且由图3可以看出，2 ms延期时间下，爆破振动强度最低，其波形速度峰值依次为1、3、4和5 ms延期时间下的69%、76%、77%和78%。故综合考虑爆破振动强度、岩体破碎效果和边坡动力效应3方面因素，试验条件下， 2 ms为最优孔间延期时间值。

4 结 论

在短毫秒延时爆破中，结构地震反应谱曲线表现出多峰特性，且峰值对应结构自振周期范围窄，为毫秒量级。单纯凭借地震反应谱峰值对结构稳定性进行动力响应及安全评价是极不合理的，应考虑结构各阶振型对系统动力响应的贡献差异因素，通过模态组合法求得结构系统反应总效应值，从而对结构动力效应及其稳定性进行评价。精确毫秒延时控制爆破中，合理孔间延期时间的选取除了应考虑爆破地震动强度、岩体爆破效果双重因素外，还需综合考虑结构物动力效应特性这一因素。试验条件下，孔间合理延期时间为2 ms。

[1] Turkmen H S.Structural response of laminated composite shells subjected to blast loading:comparison of experimental and theoretical methods[J].Journal of Sound and Vibration，2002，249(4)：663-678.

[2] Hao H，Wu C Q.Numerical study of characteristics of underground blast induced surface ground motion and their effect on above-ground structures，Part II:Effects on structural responses[J].Soil Dynamics and Earthquake Engineering，2005，25(1):39-53.

[3] 吴 琛，周瑞忠.长周期结构地震瞬态反应研究[J].振动与冲击，2011，30(5):123-126. Wu Chen，Zhou Ruizhong.Earthquake transient response of a long period structure[J].Journal of Vibration and Shock，2011，30(5):123-126.

[4] 何文福，刘文光，杨 骁，等.隔震结构弹塑性反应谱分析研究[J].振动与冲击，2010，29(1):30-33. He Wenfu，Liu Wenguang，Yang Xiao，et al.Elasto-plastic response spectra of isolated structures[J].Journal of Vibration and Shock，2010，29(1):30-33.

[5] 李夕兵，凌同华.爆炸参量对爆破地震反应谱的影响[J].爆炸与冲击，2004，24(5):443-447. Li Xibing，Ling Tonghua.Influence of explosion parameters on response spectrum for blast ground vibration[J].Explosion and Shock Waves，2004，24(5):443-447.

[6] 李夕兵，凌同华.单段与多段微差爆破地震的反应谱特征分析[J].岩石力学与工程学报，2005，24(15):2 409-2413. Li Xibing，Ling Tonghua.Response spectrum analysis of ground vibration induced by single deck and multi-deck blasting[J].Chinese Journal of Rock Mechanics and Engineering，2005，24(15):2409-2413.

[7] 荣立爽，孙建生.岩塞爆破的振动加速度反应谱分析[J].太原理工大学学报，2008，39(4):415-417. Rong Lishuang，Sun Jiansheng.Analysis of rock plug blasting vibration acceleration response spectrum[J].Journal of Taiyuan University of Technology，2008，39(4):415-417.

[8] 唐鸿卿，吴新霞.频率对爆破地震反应谱的影响[J].爆破，2008，25(4):17-19. Tang Hongqing，Wu Xinxia.Impact analysis of frequency on blasting vibration response spectrum[J].Blasting，2008，25(4):17-19.

[9] 李洪涛，卢文波，舒大强，等.隧洞开挖爆破地震反应谱特征研究[J].爆炸与冲击，2008，28(4):331-334. Li Hongtao，Lu Wenbo，Shu Daqiang，et al.Response spectrum of blasting vibration induced by tunnel excavation[J].Explosion and Shock Waves，2008，28(4):331-334.

[10] 娄建武，龙 源，方 向，等.基于反应谱值分析的爆破震动破坏评估研究[J].爆炸与冲击，2003，23(1):4l-46. Lou Jianwu，Long Yuan，Fang Xiang，et al.Study on blasting vibration damage based on response spectrum[J].Explosion and Shock Waves，2003，23(1):41-46.

[11] 孙新建，孙建生，刘 婧.基于相对位移反应谱分析的岩石爆破震动损伤评估[J].水力发电学报，2011,30(6):127-132. Sun Xinjian，Sun Jiansheng，Liu Jing.Study on damage fracture of rock blasting using spectrum of relative displacement[J].Journal of Hydroelectric Engineering，2011,30(6):127-132.

[12] 包 辉.基于反应谱分析的建(构)筑物爆破振动响应安全评估方法研究[J].工程爆破，2011,17(2):82-88. Bao Hui.Study on safety assessment method of blasting vibration response based on response spectrum[J].Engineering Blasting，2011,17(2):82-88.

[13] 王 凯，吴腾芳，季茂荣.微差爆破地震反应谱的研究[J].爆破，1997，14(4):1-6. Wang Kai，Wu Tengfang，Ji Maorong.Research and application of vibration response spectrum in millisecond blasting[J].Blasting，1997，14(4):1-6.

[14] 丁刚德，王伟策，陈小波.微差爆破的爆破地震反应谱分析[J].爆破，1997，14(3):24-30. Ding Gangde，Wang Weice，Chen Xiaobo.Research on vibration response spectrum of millisecond delay blasting[J].Blasting，1997，14(3):24-30.

[15] 魏晓林，郑炳旭.干扰减振控制分析与应用实例[J].工程爆破，2009，15(2):1-6. Wei Xiaolin，Zheng Bingxu.Analysis of control blasting induced vibration and practice[J].Engineering Blasting，2009，15(2):1-6.

[16] 张光雄，杨 军，卢红卫.毫秒延时爆破干扰降振作用研究[J].工程爆破，2009，15(3):17-21. Zhang Guangxiong，Yang Jun，Lu Hongwei.Research on seismic wave interference effect of millisecond blasting[J].Engineering Blasting，2009，15(3):17-21.

[17] 何 理，钟冬望，刘建程，等.微差爆破试验及爆破振动能量的小波包分析[J].金属矿山，2014(6):10-15. He Li，Zhong Dongwang，Liu Jiancheng，et al.Millisecond blasting tests and wavelet packet analysis of blasting vibration energy [J].Metal Mine，2014(6):10-15.

[18] 杨年华，张 乐.爆破振动波叠加数值预测方法[J].爆炸与冲击，2012，32(1):84-90. Yang Nianhua，Zhang Le.Blasting vibration waveform prediction method based on superposition principle[J].Explosion and shock waves,2012,32(1):84-90.

[19] 李顺波，杨 军，陈 浦，等.精确延时控制爆破振动的实验研究[J].爆炸与冲击，2013，33(5):513-518. Li Shunbo，Yang Jun，Chen Pu，et al.Experimental study of blasting vibration with precisely-controlled delay time[J].Explosion and Shock Waves，2013，33(5):513-518.

[20] 赵明生，张亚文，徐海波，等.不同微差间隔下爆破振动信号的反应谱分析[J].爆破，2011，28(1):28-32. Zhao Mingsheng，Zhang Yawen，Xu Haibo，et al.Response spectrum analysis of blasting vibration signal with different microsecond delay time[J].Blasting，2011，28(1):28-32.

[21] 张晓志，谢礼立，于海英.地震动反应谱的数值计算精度和相关问题[J].地震工程与工程振动，2004,24(6):15-26. Zhang Xiaozhi，Xie Lili，Yu Haiying.Precision problems in calculating response spectra by using numerical method[J].Earthquake Engineering and Engineering Vibration，2004,24(6):15-26.

[22] 付 强，袁寿其，朱荣生，等.1 000 MW核电站SEC系统鼓型滤网抗震计算[J].核动力工程，2010,31(6):10-14. Fu Qiang，Yuan Shouqi，Zhu Rongsheng，et al.Seismic analysis for SEC drum-shaped filter of 1 000 MW nuclear power plant [J].Nuclear Power Engineering，2010,31(6):10-14.

[23] 李力斌，徐贵章.结构地震反应模态组合方法述评[J].重庆建筑工程学院学报，1988(3):43-47. Li Libin，Xu Guizhang.A review of mode-superposition models in earthquake engineering[J].Journal of Chongqing Institute of Architecture and Engineering，1988(3):43-47.

(责任编辑 石海林)

Response Spectrum Research of Blasting Seismic Induced by Controlled Blasting with Precise Millisecond Delay

He Li Zhong Dongwang Tu Shengwu Cao Peng

(CollegeofScience，WuhanUniversityofScienceandTechnology，Wuhan430065，China)

The response spectrum theory widely applied in earthquake engineering was employed to investigate blasting seismic wave induced by controlled blasting with precise delay time interval.The similar model test of slope excavation was designed and carried out.The influence of different millisecond delay to response spectrum property was analyzed.Considering the interaction between intensive modes，the modal combination was conducted combined with method of second item combination completely (CQC) to obtain total effect value of structural response.The results shows that，the response spectrum curves of controlled blasting with short millisecond delay have multiple distinct peak points，and the corresponding period is usually within a narrow range of a few milliseconds.With the increase of milliseconds delay between blasting holes，the natural frequency corresponding to response spectrum peak gradually close to the natural frequency of structures，which is detrimental to the safety of the structure.Choosing of reasonable delay time interval should comprehensively consider blasting vibration intensity，blasting effect of rock mass and dynamic response of construction.Under experimental conditions，the reasonable delay time interval between blasting holes is 2 ms.

Slope，Blasting vibration，Response spectrum，Modal combination，Method of CQC，Delay time interval

2015-06-07

国家自然科学基金项目(编号：51174147)，湖北省自然科学基金项目(编号：2012FFA135)，武汉科技大学研究生创新基金项目(编号：JCX0017)。

何 理(1986—)，男，讲师，博士。通讯作者 钟冬望(1963—)，男，教授，博士研究生导师。

O382,TD235

A

1001-1250(2015)-10-011-07