基于Pro/ENGINEER的凸轮机构的动态分析设计

赵仙花 张毅

（1.德州学院汽车工程系，山东德州 253023；2.中轻集团长沙长泰机械股份有限公司，湖南长沙 410116）

基于Pro/ENGINEER的凸轮机构的动态分析设计

赵仙花1张毅2

（1.德州学院汽车工程系，山东德州 253023；2.中轻集团长沙长泰机械股份有限公司，湖南长沙 410116）

文章主要是利用Pro/E软件对凸轮机构进行参数化设计和三维建模，在此基础上对其进行了运动仿真分析和动态分析，为设计人员所设计的凸轮机构进一步方便而快速的改进和优化提供依据。这对提高凸轮机构的性能、设计质量和效率具有实际价值和长远意义。

凸轮机构；参数化设计；运动仿真；动态分析

0.引言

凸轮机构是一种结构简单紧凑、响应快速，但又能实现各种复杂运动的一种机构，广泛应用于各种自动机械、仪器和操纵控制装置[1]。而且由于其结构上的优点使得凸轮机构不可能被数控、电控等装置完全替代。因此，凸轮机构的设计、运动分析及其动力学问题的分析研究也愈来愈重要。利用Pro/E不仅可以快速准确地进行凸轮机构的三维实体造型，直观地再现出产品的外观，并可以利用Mechanism和Mechanica模块进行运动仿真和动态分析，来验证机构的合理性、可行性，通过分析再利用Pro/E的二次开发工具模块Program就能够很方便地实现凸轮的参数化设计，对凸轮机构设计进行修正，生成新的凸轮机构。这样，可以减少了繁琐的重复劳动，从而大大提高了设计效率和精度。

1.凸轮机构的参数化建模

1.1 凸轮的可变参数

凸轮的可变参数包括基圆半径、行程、推程角、远休角、回程角、近休角、滚子半径、偏距、孔径、凸轮厚度等。

1.2 基本设计思路

（1）根据从动件运动规律及结构要求进行设计，获得以极坐标或直角坐标表示的凸轮理论廓线方程，以及上述各参数。滚子半径为0，对应尖顶从动件，而偏距为0，对应对心从动件。因此，实现参数化设计，可涵盖较多类型的凸轮机构。

（2）在Pro/E【程序】编辑器中，设定上述各参数，并在退出后输入各参数值。

（3）利用Pro/E的【方程】功能，分别绘制凸轮理论廓线，其表达式中带入前面设定的各变量名。

（4）绘制一条由分段理论廓线组成的封闭曲线，即完整的凸轮理论廓线。

（5）生成凸轮实体。在生成过程中要隐藏分段曲线，即利用封闭曲线，并加入滚子半径参数。

（6）加入参变量，实现参数化。

1.3 设计步骤

（1）创建新的零件文件

文件→新建→输入零件名称→确定

（2）参数输入

工具→程序→编辑设计→打开记事本，在INPUT和END INPUT之间输入参数如下，存盘并退出。

INPUT

jybj NUMBER；基圆半径

h NUMBER；行程

tcj NUMBER；推程角

yxj NUMBER；远休角

hcj NUMBER；回程角

jxj NUMBER；近休角

gzbj NUMBER；滚子半径

kj NUMBER；孔径

pj NUMBER；偏距

hd NUMBER；厚度

END INPUT

→在信息窗口选“是”，以便输入参数值→输入→选取全部→完成选取

根据信息窗口提示，各参数赋初值如下：jybj=60；h=60；tcj=110；yxj=100；hcj=100；jxj=50；gzbj=10；kj=30；pj=0；hd=35

（3）分段绘制理论廓线

根据上述原理，以设计正弦加速度运动规律的凸轮为例，利用方程曲线功能，分段绘制凸轮理论廓线如下。

推程段：

插入基准曲线→从方程→完成→选择系统默认坐标系→选择坐标系类型为圆柱坐标系→进入方程编辑器。输入曲线方程表达式如下，保存，退出编辑器。

theta1=tcj*t

r0=sqrt(jybj*jybj-pj*pj)

r1=r0+h*(t-sin(360*t)/2/pi)

theta=theta1+atan(pj/r0)

r=sqrt(pj*pj+r1*r1)

z=0

其它三段曲线的绘制方法同上，对应的曲线方程分别为：

远休段：

theta1=tcj+yxj*t

r0=sqrt(jybj*jybj-pj*pj)

r1=r0+h

theta=theta1+atan(pj/r0)

r=sqrt(pj*pj+r1*r1)

z=0

回程角：

theta1=tcj+yxj+hcj*t

r0=sqrt(jybj*jybj-pj*pj)

r1=r0+h*(1-t+sin(360*t)/2/pi)

theta=theta1+atan(pj/r0)

r=sqrt(pj*pj+r1*r1)

z=0

近休角：

theta1=tcj+yxj+hcj+jxj*t

r0=sqrt(jybj*jybj-pj*pj)

r1=r0

theta=theta1+atan(pj/r0)

r=sqrt(pj*pj+r1*r1)

z=0

（4）分段廓线连成整体

（5）生成凸轮实体

为了避免在后面的曲线点选过程中出现干扰，隐藏分段绘制的4段曲线，使画面上仅存封闭曲线。在左侧模型特征树中点选相应的曲线，右键→隐藏即可。

现有理论廓线为对应尖顶推杆或滚子推杆对应滚子中心的凸轮廓线，在滚子推杆情况下，凸轮实际廓线应考虑滚子半径。可利用等距偏置线功能完成如下：

图1 凸轮三维模型

（6）特征参数化

在上述建模过程中，凸轮廓线由于是以方程曲线方式建立的，因而已经实现参数化了。但滚子半径、凸轮厚度以及孔径尚未实现参数化，需使其成为变量，与先前在程序中设定的gzbj、hd和kj等参数相联系。具体方法如下：

滚子半径与厚度参数化：点击凸轮实体→模型特征树对应项呈高亮显示→右键点击该项→编辑→途中将显示偏置距离10以及凸轮厚度35→工具→关系→上述尺寸值将变为参数符号，并弹出关系对话框，对应参数符号d1、d0输入：d1=pj、d0=hd→确定。

孔径参数化：点击轴孔→模型特征树对应项呈高亮显示→右键点击该项→编辑→工具→关系→上述尺寸值将变为参数符号，并弹出关系对话框，对应参数符号d2输入：d2=kj→确定。

（7）凸轮变参

改变各参数值，可获得不同的凸轮廓线、凸轮厚度及孔径。具体做法：点击图标：→→输入→在弹出的对话框内，点选需要变参的项目→完成选取→在弹出的信息窗口内，输入相应参数值→点击图标。

对应不同参数组的凸轮模型如图2所示。其中gzbj=0和pj=0对应对心尖顶推杆。

图2 参数化的凸轮模型

2.凸轮机构的装配

通过Pro/E软件的装配模块Assembly，将先前建立的凸轮机构中的各零件：机架、凸轮、滚子、轴销以及推杆进行装配，完成凸轮机构的创建。新建一个asm文件，点添加组件，逐一添加组件并定义互相接触的零件间的连接类型，使它们具有相应的运动自由度。在Pro/E系统的装配模式中，以系统缺省位置固定机架零件作为基础，使用销钉连接方式分别连接凸轮与机架、滚子与推杆；并用滑动杆连接方式连接推杆与机架。装配图如图3所示。并检查组件间是否会发生运动干涉。

图3 凸轮机构的装配图

3.凸轮机构的运动仿真和动态分析

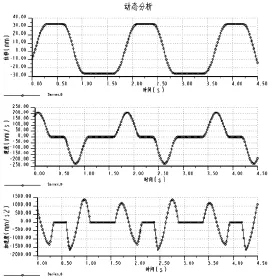
图4 位移、速度、加速度分析图

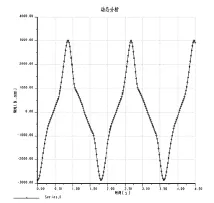
图5 轴转矩

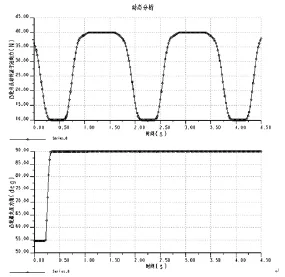
图6 凸轮与从动件滚子法向力、凸轮最大压力角

4.结语

利用Pro/E软件的强大三维实体建模功能和二次开发工具模块Program可以很方便地实现凸轮的参数化设计，直观地再现出产品的外观，而且设计精度好、效率高。并可以Pro/E中的Mechanism和Mechanica两个模块进行运动仿真和动态分析，对凸轮机构的位移、速度、加速度、凸轮压力角、轴的受力、扭矩、凸轮与推杆之间的作用力等量进行测量分析，分析机构性能，以此来检验机构的合理性、可行性，并为设计人员提供修改依据，协助设计人员更好地、更快地完成产品的设计工作，使产品能更好地满足工程和性能要求。而且由于凸轮机构实行了参数化设计，所以，修改时非常方便，设计人员只要对已有的凸轮机构模型的参数进行变更就可以生成新的凸轮机构。对于减少产品的试验环节、提高产品性能和质量以及设计效率、降低成本有着非常重要的意义。

[1]孙恒，陈作模.机械原理（第七版）[M].北京：高等教育出版社，2006：151-152.

[2]王咏梅.Pro/ENGINEER Wildfire 4.0中文版基础教程[M].北京:清华大学出版社，2008.

[3]张继春，杨建国.装配设计与运动仿真及Pro/E实现[M].北京:国防工业出版社，2006.

[4]祝凌云，李斌.PROE运动仿真和有限元分析[M].北京:人民邮电出版社，2004.

[5]张华，郭荣春，周进.挖掘机动臂在Pro/E中的动态模拟与分析[J].农业装备与车辆工程，2005，（1）:26－27.

（责任编辑 陈永康）

TH112.2

A

1008－7257（2015）02－0105－03

2014－07－14

赵仙花（1977－），女，山西忻州人，德州学院讲师，硕士，研究方向：机械设计及制动化。