CFS－PML在探地雷达FDTD法模拟中应用

石 明，冯德山，吴 奇

（1.中南大学 地球科学与信息物理学院，湖南 长沙 410083；2.贵州省有色金属和核工业地质勘查局 物化探总队，贵州 都匀 558004；3.中南大学 有色资源与地质灾害探查湖南省重点实验室，湖南 长沙 410083）

0 引 言

探地雷达（ground penetrating radar，GPR）数值模拟是地球物理重要研究内容，对建立的模型开展数值模拟能有效指导地质解释.应用时域有限差分（finite difference time domain，FDTD）法进行GPR 数值模拟时，因计算机内存空间的有限，总是在某处把网格空间截断，使之成为有限区域.这样，在网格空间截断处就会产生强烈的非物理的电磁反射干扰波.为了在截断边界处不引起虚假反射，吸收边界条件对模拟精度起着关键作用.目前在截断边界处常通过加载完全匹配层（perfectly matched layer，PML）来 改 善 吸 收 效果，但无论是PML 还是单轴各向异性完全匹配层（uniaxial anisotropic perfectly matched layer，UPML）对隐失波、低频波、大角度入射的掠角波都不能很好地吸收.为此，本文引入了复频移卷积完全匹配层（complex frequency shifted convolution perfectly matched layer，CFS－PML）以改善截断边界处对隐失波、低频波、掠角波的吸收效果.

早期提出的 Taflove－Brodwin 边界［1］、Engquist－Majda 边界［2］、Mur 边界［3］、Liao 边界［4］，通常在模拟区域的外边界仍有0.5% ～5.0%的反射系数，它们逐渐被PML 边界条件所取 代.PML边界条件最初是由Berenger 提出的［5－6］，它在FDTD网格外边界加载一种非物理的吸收媒质，使进入PML 的透射波迅速衰减，将边界条件的研究向前推进了一大步；但Berenger PML的理论体系是非Maxwell方程的，物理机制模糊，同时，其电磁场分量分裂技术增加了计算内存与数值实现的难度［7］，而且只对行波有吸收效果，对空域中衰减的隐失波、低频波以及小角度入射的掠角波无吸收效果.为了改善边界条件的吸收效果，Sacks等［8］和Gedney［9］提出了UPML.UPML不需要对电磁场分裂，计算更简洁、易编程实现，因其在吸收系数中引入了线性的吸收因子，UPML边界对隐失波、低频波等干扰波有一定的吸收效果.詹应林等［10］将UPML 应用于二维FDTD探地雷达正演中；Feng等［11－12］将UPML应用到交替方向隐式时域有限差分（ADI－FDTD）法中实现了探地雷达的二、三维数值模拟；李静等［13］开展了三维UPML边界条件的高阶FDTD探地雷达正演.尽管UPML对于隐失波、低频波等干扰波有一定的吸收效果，但仍然不是特别完美.

考虑到复频移拉伸函数的PML 技术可以吸收低频信号在边界表面的反射，同时对隐失波等大角度掠射波也有很好的吸收效果，Kuzuoglu等［14］在复频率偏移完全匹配层的变量Sk中引入低频分量吸收参数αk，将复平面的极点从实轴移动到负虚半平面上，加强了对低频波、隐失波的吸收；Roden等［15］将复频移拉伸函数加入到电磁波模拟的PML 方程，有效压制了信号的假反射；Wang等［16］将CFS－PML应用到ADI－FDTD 法中；Drossaert等［17－18］和Komatitsh 等［19］提出了基于递归积分的波场非分裂的复频移PML（recursive integration CFS－PML，简称CFSRIPML）；Zhang 等［20］和Martin 等［21］将 基 于 辅助微分方程的CFS－PML 应用到弹性波数值模拟中，该方法易于扩展到高阶差分形式；张显文等［22］将递归复频移PML应用到交错网格高阶差分弹性波波动方程正演中；张鲁新等［23］将不分裂的完全匹配层（CPML）结合旋转交错网格有限差分技术应用到孔隙弹性介质模拟中；Giannopoulos［24］和Li等［25］将基于CFS－RIPML 吸收边界技术应用在电磁波波动方程的有限差分正演中.相比常规PML、UPML 吸收边界，CFS－PML 对于隐失波、低频波等具有更好的吸收效果，所以CFS－PML有非常广阔的发展前景.

1 零极点匹配Z变换与逆Laplace变换

根据Kuzuoglu等［14］的研究，定义复坐标拉伸坐标系中的算子与拉伸变量分别为

式中：κk的引入是为了改善PML 对表面波的吸收特性；σk为PML内k方向电导率参数；αk则是为了改善PML 对低频分量的吸收特性.σk和αk为大于0的正实数，κk为大于等于1的正实数.根据式（2）中的变量（k＝x，y，z）的Z变换，利用关系式jω→s，将式（2）变换到S域，则有

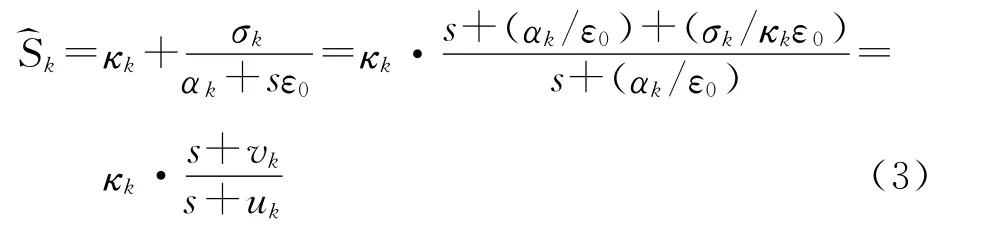
其中

然后利用零极点匹配Z变换（matchedZtransform）关系：

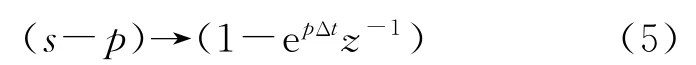
将式（3）变换到Z域

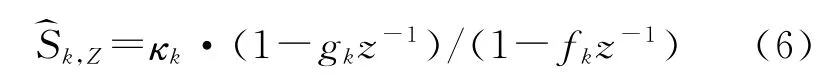
其中

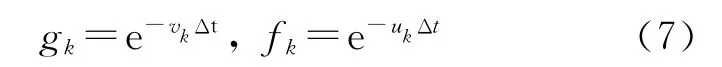
求式（3）的倒数为

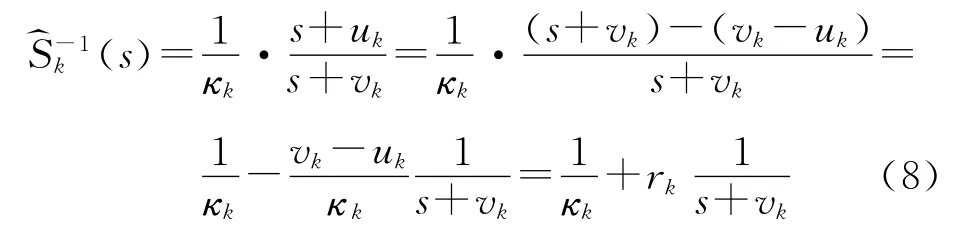
其中

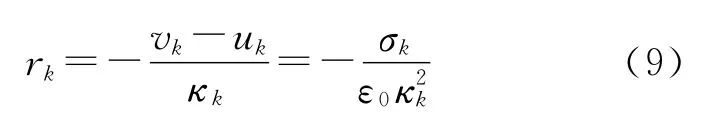
定义倒数的逆Laplace变换为则式（8）的拉普拉斯逆变换为［26］

式中：δ（t）是单位冲激函数，u（t）是单位阶跃函数，ζk（t）为

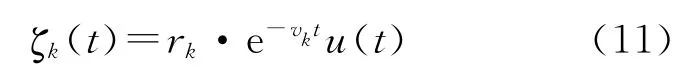
2 二维TM 波的CFS－PML 边界条件推导

由电磁波传播理论可知［27］，GPR遵循的Maxwell方程的6个耦合偏微分方程在二维情况下变为3个偏微分方程，共有Ez、Hx、Hy3个分量，称之为TM 波：

其中E为电场强度，V／m；H为磁场强度，A／m；ε为介电常数，F／m；μ为磁导率，H／m；σe为电导率，S／m；σm为等效磁阻率，Ω／m.

将频率域方程（13）～（15）进行反Fourier变换，并将式（10）代入，可得到时域方程

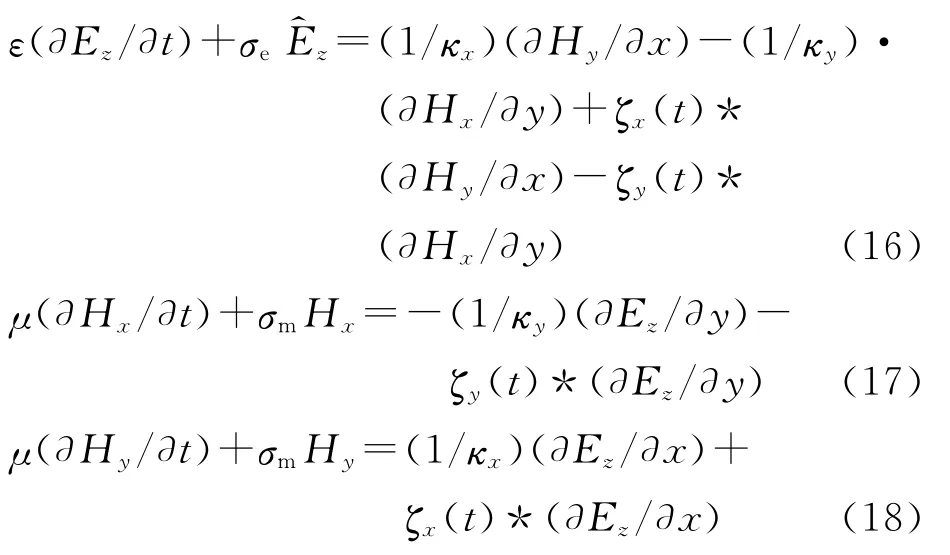
式（16）～（18）中涉及时域卷积的计算，直接计算效率较低，为了有效地计算方程中的卷积，根据离散脉冲ζk（t）的定义，可得到

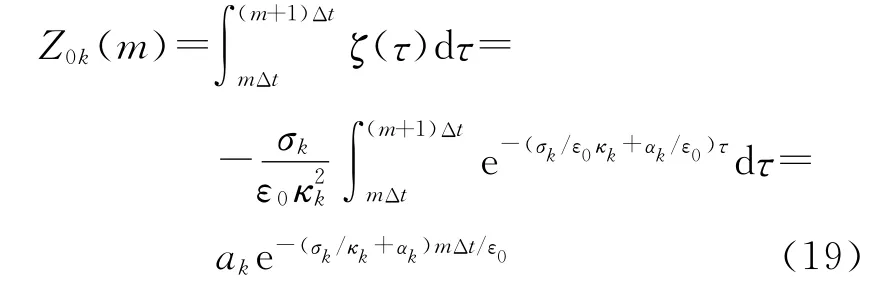
其中

将式（19）和（20）代入式（16）～（18）可得到：En＋1z（i，j）＝CA（m）·Enz（i，j）＋CCx（m）·

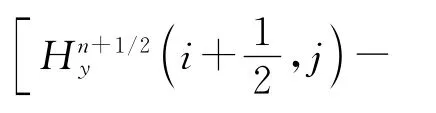
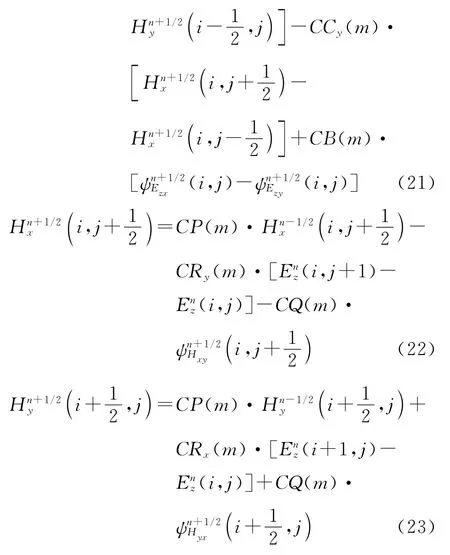
其中ψEzx、ψEzy、ψHxy和ψHyx为引入的辅助变量，它们可采用递归卷积方法计算：

符号标记CA（m）～CRy（m）中的电磁参数标号m的取值与式（21）～（23）中右端电场或磁场分量的空间位置相同，其表达式如下：

在二维情况下，模型内部κx＝κy＝1，σx＝σy＝0，αx＝αy＝0，Sx＝Sy＝1.在CFS－PML 边界区域，这些参数被赋予不同的值，设σx和σy大于0，允许传播的波被吸收，另一方面，使κx和κy大于1，有利于CFS－PML区域吸收衰减波.αx和αy大于0，能提高对低频波的吸收.为使CFS－PML 达到最优吸收效果，设置吸收参数从CFS－PML 外边界到内边界逐步减小到0.对κx和κy有

其中d（0≤d≤δ）为CFS－PML 内的计算点到CFS－PML区域内边界的距离；δ为CFS－PML 区域的厚度，计算过程中常取8～10个空间网格步长.m被称为CFS－PML 的指数参数，κkmax为参数κk的最大值.对于参数σx和σy有

因为坐标扩展变量是一维函数，这里κk和σk只沿k（x或y）方向变化.为了衰减波的有效吸收，在常见的程序计算中常设置：

3 CFS－PML吸收边界条件效果分析

3.1 均匀介质中边界条件对比

建立图1所示3.0 m×3.0 m 的模型，模型中均匀介质相对介电常数为10，电导率为0.002 S／m，在模型的中心加入500 MHz的脉冲Ricker子波，应用不带边界条件及加入不同边界条件的FDTD 法对该模型进行正演，以说明不同边界条件的优劣，正演中取网格空间步长为dx＝dy＝0.005m，dt＝11.79×10－12s，时窗长度为3.5×10－8s.

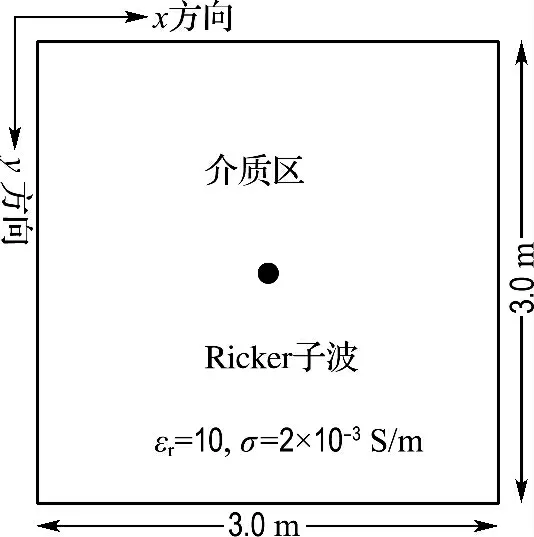
图1 均匀介质模型示意图Fig.1 The sketch map of homogeneous medium model

图2为不加载任何边界条件正演所得的15、22、30ns雷达波场快照；由图2（a）的15ns快照中可见，雷达波以圆形方式向外传播；图2（b）雷达波在截断边界的4条边、4个角点引起了较强的虚假反射波；图2（c）截断反射波又以原波前相反方向传播，从左边的电场数量级上可以看出，该截断反射波的能量较强，取值在－200～200V／m变化，几乎与一次波前的能量在一个数量级.

图3（a）为采用二阶Mur吸收边界处理截断边界后的30ns波场快照，4条边的人为截断强反射波得到了很好的吸收，仅4个角点处的边界反射波仍然可见；但从左边的电场取值范围0.5～1.0V／m 不难看出，Mur边界条件对边界处反射波起了较好的吸收作用，但是效果仍然有待提高.图3（b）、（c）分别为加入UPML 吸收边界、CFSPML吸收边界30ns的波场快照，内部区域仍清晰可见4条截断边界处的反射，但是4个角点处的反射消失不见，再看左边的电场取值范围，显然4条边界的反射波能量是非常弱的，其能量在－0.1～0.1 V／m 变化，说明这两种边界条件较二阶Mur吸收边界条件有数量级的提高.

3.2 UPML与CFS－PML吸收效果对比验证

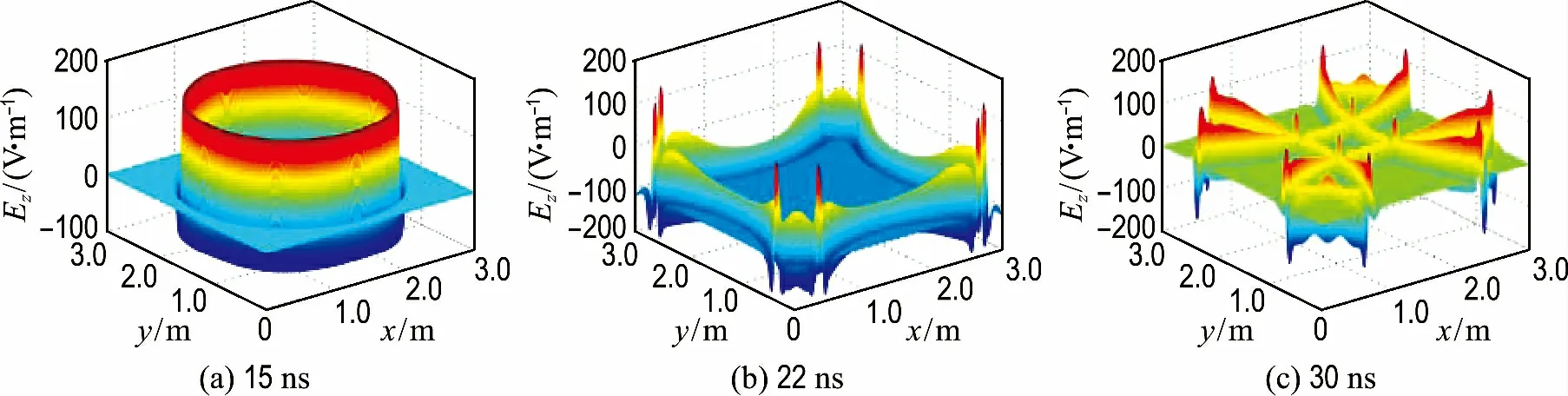
图2 无边界条件时的不同时刻波场快照三维显示Fig.2 The 3Dvisualization map of wave field snapshots at different time without boundary condition

图3 加载不同边界条件的30ns波场快照三维显示Fig.3 The 3Dvisualization map of wave field snapshots at 30ns with different boundary conditions

为了对比UPML 与CFS－PML 边界条件对隐失波、低频波以及小角度入射的掠角波等干扰波的吸收效果，设置图4所示双层介质模型，模型尺寸为4.0m×1.0m，模型中上层介质1的介电常数为6.0，电导率为0.020S／m，介质2的介电常数为3.0，电导率为0.001S／m，在S（x＝2.0 m，y＝0.1m）位置加入一个频率为900 MHz的Ricker子波脉冲，分别应用8个网格的UPML与CFS－PML边界条件的FDTD 法对该模型进行正演，正演中取网格空间步长为dx＝dy＝0.005m，dt＝11.79×10－12s，指数参数m＝4，CFS－PML的κkmax＝5，时窗长度为4.0×10－8s.

图4 双层介质模型Fig.4 Model of double－layer medium

图5、6为8、10、12、15、20、25ns的电场分量Ez的波场快照，其中图5为UPML 吸收边界，图6为CFS－PML吸收边界.首先取最大值的0.5%设为阈值，将小于该阈值的波场值置零，为了加强小振幅的显示，以0.3为幂进行归一化.图5、6为经过上述处理，归一化后的波场快照.从图5可以看出，对于狭长模型或井筒模型，以掠射角入射的雷达波在模型边界上产生虚假的反射，作为有效波的干扰回到模型区域内，UPML上边界上产生一系列的呈有规律分布的虚假反射波.而Kuzuoglu等［14］提出的CFS－PML 拉伸函数将奇异性 由实轴移到复平面的负虚半轴，改善了吸收边界性能.从图6可以看出，基于CFS－PML 吸收边界法对入射到边界层内波的能量进行了充分的吸收，即使对于以掠射角入射到边界层内的狭长模型吸收效果也较UPML理想.

3.3 吸收边界的全局反射误差分析

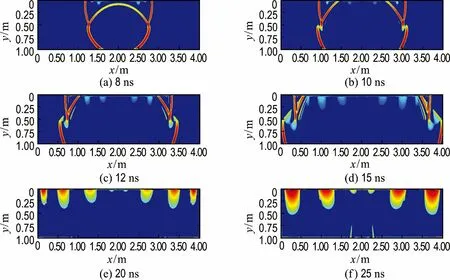
图5 UPML边界条件下的电场分量Ez 不同时刻波场快照Fig.5 The wave field snapshots of electric field component Ezat different time under UPML boundary condition

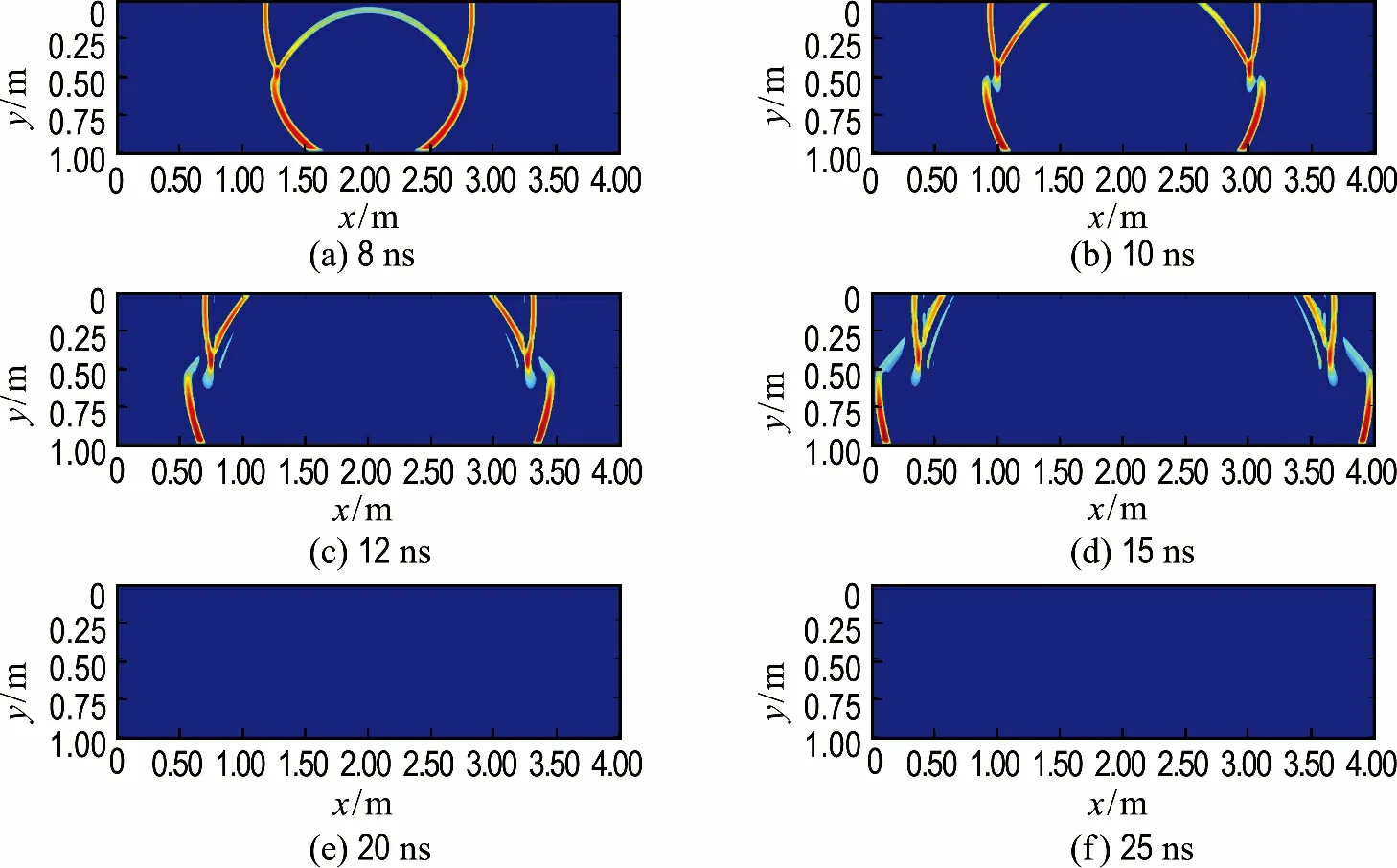
图6 CFS－PML边界条件下的电场分量Ez 不同时刻波场快照Fig.6 The wave field snapshots of electric field component Ezat different time under CFS－PML boundary condition

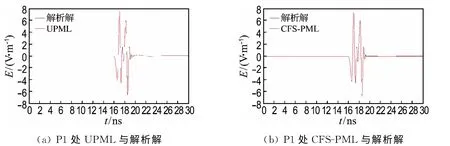
图7 P1处UPML和CFS－PML与解析解对比图Fig.7 The comparison map of UPML，CFS－PML and analytical solution at P1position

全局反射误差是反映吸收边界吸收性能的关键参数，它能反映一种边界条件在整个区域模拟计算中的误差精度.为了说明CFS－PML 与UPML的吸收效果，仍以图4所示的模型为例，观测点P1的坐标为（0.08m，0.08m）.图7（a）、（b）分 别 为 加 载UPML 和CFS－PML 吸 收 边 界FDTD 法正演所得信号与精确信号的拟合曲线，其中的精确信号为将模型区域扩大至原模型4倍而获得的信号.从图7中可以看出，观测点P1处CFS－PML与解析解拟合更好，而UPML 在边界处因掠射波、低频波不能被较好吸收，在19ns左右与解析解拟合得并不太好.通过模拟计算对比验证CFS－PML、UPML 两种吸收边界在观测点与激励源位置角度最大的P1 点的全局反射误差，以更直观地充分反映吸收边界的整体吸收效果.全局反射误差的获得是通过在设置激励源与观测点位置关系的基础上，分别采用正常模型和扩大4倍模型获得观测点处的实测接收信号Es和参考模型信号Eref，并求取参考模型信号中振幅最大的值Erefmax，通过以下计算公式获得全局反射误差：

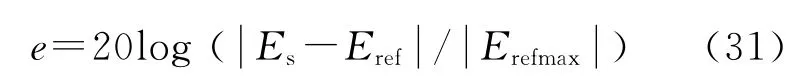
通过设置相同的观测参数及吸收边界层数获得了两种不同吸收边界的反射误差对比，如图8所示，CFS－PML吸收边界的反射误差相比UPML 吸收边界其整体误差更小，说明CFS－PML 吸收边界较UPML有一定幅度的提高与改善.

图8 P1处两种吸收边界反射误差对比图Fig.8 The comparison map of reflection error under UPML and CFS－PML at P1position

4 结 论

（1）推导了CFS－PML边界条件的GPR 正演FDTD 差分公式，应用均匀介质中GPR 波场边界处的传播快照，对比没有加载边界条件、加载Mur、UPML、CFS－PML 边界处的波场反射波的强弱，实例结果表明UPML 与CFS－PML 能较好地处理GPR 截断边界，具有较好的吸收效果.

（2）设置双层介质狭长模型对比了UPML与CFS－PML的吸收效果，波场快照与全局反射误差都 说 明，CFS－PML 较UPML 对 隐 失 波、低 频波、掠角波有更高效的吸收，非常适合于宽频带脉冲GPR 正演中FDTD 法的吸收边界.由于CFSPML边界条件的优良吸收特性，其能广泛地应用于电磁场仿真、无线传播、电磁兼容、微波技术等领域的FDTD 计算中.

［1］ Taflove A，Brodwin M E.Numerical solution of steady－state EM scattering problems using the timedependent Maxwell′s equations ［J］.IEEE Transactions on Microwave Theory and Techniques，1975，23（8）：623－630.

［2］ Engquist B，Majda A.Absorbing boundary conditions for the numerical simulation of waves［J］.Mathematics of Computation，1977，31（139）：629－651.

［3］ Mur G.Absorbing boundary conditions for the finite－difference approximation of the time－domain electromagnetic－field equations ［J］.IEEE Transactions on Electromagnetic Compatibility，1981，EMC－23（4）：377－382.

［4］ LIAO Zhen－peng，Wong H L，YANG Bai－po，et al.A transmitting boundary for transient wave analyses ［J］.Science in China，Ser.A，1984，27（10）：1063－1076.

［5］ Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1994，114（2）：185－200.

［6］ Berenger J P.Three－dimensional perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1996，127（2）：363－379.

［7］ 葛德彪，闫玉波.电磁波时域有限差分方法［M］.西安：西安电子科技大学出版社，2005：67－81.GE De－biao，YAN Yu－bo.Finite－Difference Time－Domain Method for Electromagnetic Waves ［M］.Xi′an：Xidian University Press，2005：67－81.（in Chinese）

［8］ Sacks Z S，Kingsland D M，Lee R，etal.Perfectly matched anisotropic absorber for use as an absorbing boundary condition ［J］.IEEE Transactions on Antennas and Propagation，1995，43（12）：1460－1463.

［9］ Gedney S.An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattice［J］.IEEE Transactions on Antennas and Propagation，1996，44（12）：1630－1639.

［10］ 詹应林，昌彦君，曹中林.基于UPML 吸收边界的探地雷达数值模拟研究［J］.资源环境与工程，2008，22（2）：235－238.ZHAN Ying－lin，CHANG Yan－jun，CAO Zhonglin.Modeling of ground penetrating radar based on UPML boundary conditions ［J］.Resources Environment and Engineering，2008，22（2）：235－238.（in Chinese）

［11］ FENG De－shan，DAI Qian－wei.GPR numerical simulation of full wave field based on UPML boundary condition of ADI－FDTD［J］.NDT ＆ E International，2011，44（6）：495－504.

［12］ 冯德山，谢 源.基于单轴各向异性完全匹配层边界条件的ADI－FDTD三维GPR 全波场正演［J］.中南大学学报（自然科学版），2011，42（8）：2363－2371.FENG De－shan，XIE Yuan.Three dimensional GPR numerical simulation of full wave field based on UPML boundary condition of ADI－FDTD ［J］.Journal of Central South University（Science and Technology），2011，42（8）：2363－2371.（in Chinese）

［13］ 李 静，曾昭发，黄 玲，等.三维探地雷达数值模拟中UPML 边界研究［J］.物探化探计算技术，2010，32（1）：6－12.LI Jing，ZENG Zhao－fa，HUANG Ling，etal.Study of UPML boundary for three dimensional GPR simulation ［J］.Computing Techniques for Geophysical and Geochemical Exploration，2010，32（1）：6－12.（in Chinese）

［14］ Kuzuoglu M，Mittra R.Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers［J］.IEEE Microwave and Guided Wave Letters，1996，6（12）：447－449.

［15］ Roden J A，Gedney S.Convolutional PML（CPML）：an efficient FDTD implementation of the CFS－PML for arbitrary media［J］.Microwave and Optical Technology Letters，2000，27（5）：334－339.

［16］ WANG Lin－nian，LIANG Chang－hong.A new implementation of CFS－PML for ADI－FDTD method［J］.Microwave and Optical Technology Letters，2006，48（10）：1924－1928.

［17］ Drossaert F H，Giannopoulos A.A nonsplit complex frequency－shifted PML based on recursive integration for FDTD modeling of elastic waves［J］.Geophysics，2007，72（2）：9－17.

［18］ Drossaert F H，Giannopoulos A.Complex frequency shifted convolution PML for FDTD modeling of elastic waves［J］.Wave Motion，2007，44（7－8）：593－604.

［19］ Komatitsch D，Martin R.An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation ［J］.Geophysics，2007，72（5）：155－167.

［20］ ZHANG Wei，SHEN Yang.Unsplit complex frequency－shifted PML implementation using auxiliary differential equations for seismic wave modeling［J］.Geophysics，2010，75（4）：141－154.

［21］ Martin R，Komatitsch D，Gedney S，etal.A highorder time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary differential equations（ADE－PML）［J］.Computer Modeling in Engineering and Sciences，2010，56（1）：17－40.

［22］ 张显文，韩立国，黄 玲，等.基于递归积分的复频移PML弹性波方程交错网格高阶差分法［J］.地球物理学报，2009，52（7）：1800－1807.ZHANG Xian－wen，HAN Li－guo，HUANG Ling，etal.A staggered－grid high－order difference method of complex frequency－shifted PML based on recursive integration for elastic wave equation［J］.Chinese Journal of Geophysics，2009，52（7）：1800－1807.（in Chinese）

［23］ 张鲁新，符力耘，裴正林.不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用［J］.地 球 物 理 学 报，2010，53（10）：2470－2483.ZHANG Lu－xin，FU Li－yun，PEI Zheng－lin.Finite difference modeling of Biot′s poroelastic equations with unsplit convolutional PML and rotated staggered grid［J］.Chinese Journal of Geophysics，2010，53（10）：2470－2483.（in Chinese）

［24］ Giannopoulos A.An improved new implementation of complex frequency shifted PML for the FDTD method ［J］.IEEE Transactions on Antennas and Propagation，2008，56（9）：2995－3000.

［25］ LI Jing，ZENG Zhao－fa，HUANG Ling，etal.GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD［J］.Computers and Geosciences，2012，49：121－130.

［26］ 李建雄.时域有限差分法中完全匹配层的实现算法研究［D］.天津：天津大学，2007.LI Jian－xiong.Research on algorithms for implementing perfectly matched layers in the finite difference time domain method［D］.Tianjin：Tianjin University，2007.（in Chinese）

［27］ Yee K S.Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media［J］.IEEE Transactions on Antennas and Propagation，1996，14（3）：302－307.