一种无线网络控制系统概率性任务实时调度算法
林 强,吴国伟,刘玥瑶,王文超
(1.大连理工大学 软件学院,辽宁 大连 116024;2.大连科技学院,辽宁 大连 116052)
0 引 言
无线网络控制系统(wireless networked control system,WNCS)是当前社会各界广泛关注的研究领域,是涉及多学科、知识高度集成的前沿热点[1].WNCS 的核心部分是传感器网络,系统通常包括传感器节点、汇聚节点和管理节点.在监测区域内部或附近随机放置大量传感器节点,监测数据顺着传感器的节点传输,经过多跳后路由到汇聚节点,最后通过互联网或卫星到达管理节点.用户通过管理节点对传感器网络进行配置和管理,发布监测任务以及收集监测数据.
传感器网络节点的组成和功能包括如下4个基本单元:传感单元(由传感器和模数转换功能模块组成)、处理单元(由嵌入式系统构成,包括CPU、存储器、嵌入式操作系统等)、通信单元(由无线通信模块组成)、电源.
因为无线传感器网络有自组织性、网络动态变化、消耗能量、分节点电量有限等特点[2],必须合理调度分配无线传感器网络中的任务,达到减少能量消耗、延长系统生命期、加快完成任务的速度和提高系统节点使用效率的目标[3].
自Liu和Layland在20世纪70年代初发表了关键论文以来,有关无线传感器网络实时任务调度的方法层出不穷,而这些方法的基础都是基于优先级以及截止时间优先的传统方法.最开始的调度策略是最早截止时间(EDF)[4]以及最坏情况下的调度,虽然有一些局限性,但是其思想在当时还是比较先进的.本文对无线传感器网络实时系统任务调度的研究集中在时间及优先级分配上,即在提高任务完成率的同时减少任务完成时间,提高系统性能并延长系统生命周期.
1 随机调度策略
无线传感器网络任务调度是为了把一组任务用确定的调度策略,确定其调度簇,即分配同一节点执行的任务,并且控制任务的执行顺序和时间,确保任务能够高效完成[5].
1.1 随机调度概述
自Liu和Layland提出开创性观点以来,用最坏情况方法对关键系统时间分析的研究进行了很长时间.然而这些方法在提升性能方面表现得太过悲观,因此在实时系统领域,设计实时调度算法很具挑战性.在复杂结构中,程序执行时间的变化意味着最坏情况方法会归结为系统不可行.因此,有些时候最坏情况方法限制新功能的引入,并把它作为结构的重要考量.
随机方法可以替代最坏情况方法.一般地,实时系统的可行性以系统参数各种可能出现的值的概率来表示.近年来,实时系统的随机性分析得到发展,涌现了隐式任务模型(亦称Liu和Layland模型)、复合框架模型(MF)、拓展复合框架模型(GMF)、周期实时模型(RRT)等.
随机模型是现在最具表现潜力的模型,由于它的概率性,任务的每个参数相互联系.随机模型能够描述同一个任务中不同作业之间的关系,是最接近RRT 的任务模型.
1.2 标记和定义
随机变量χ有分布函数(PF)fχ(·):fχ(x)=P(χ=x),χ∈[xmin,xmax].
随机变量的可能取值和概率的关系表示如下:
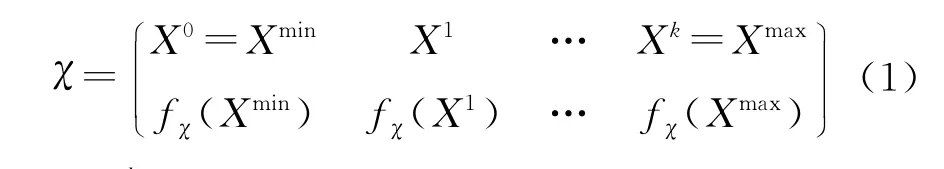
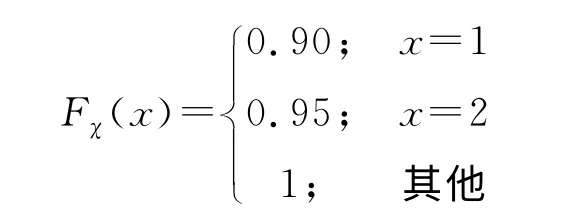
两个随机变量X和Y是相互独立的,表示一个事件的结果对另一事件无影响.
变量X和Y的卷积Z称为两个变量的累积和,即
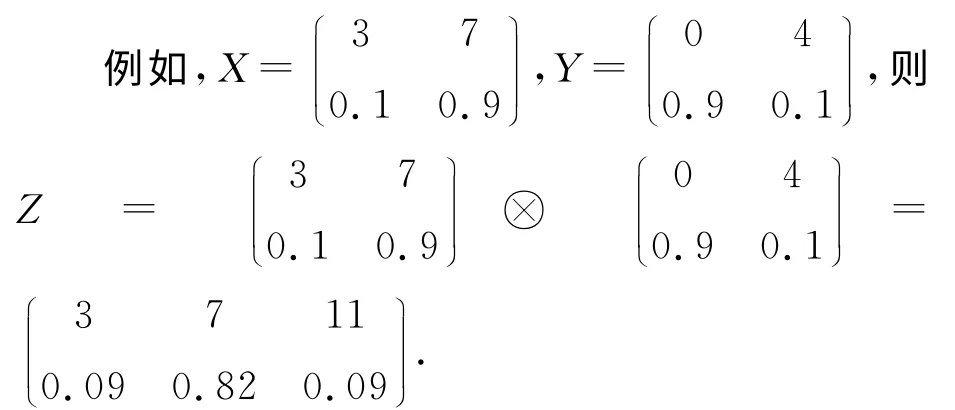
1.3 随机模型
考虑一个系统同时释放n个任务{τ1,τ2,…,τn},需要在单处理器上用固定优先级调度策略.不失一般性地,认为对于i<j,τi优先级大于τj,hp(i)表示比τi优先级高的任务集.每个任务τi产生无穷多个连续的作业τi,j,j=1,…,∞.
一项任务的一个作业的随机执行时间(pET)表示概率性的执行时间,等于一个给定的值.每个任务τi被泛化为一个不定时发生的任务[6],并且用随机最坏情况执行时间(pWCET)和随机最小到达时间(pMIT)来定义.
一项任务的pWCET 记作Ci,范围是Cji,j,并且可以用关系≥来表示:Ci≥Cji,j.从图像上看,这意味着Cji的累积分布函数一直低于Ci,j.
Ci可以写作
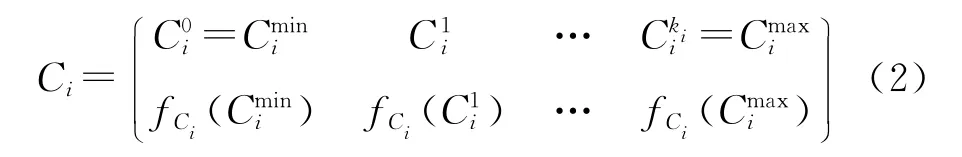
例如一个任务τi,有Ci=得出fCi(2)=0.50,fCi(3)=0.45,fCi(25)=0.05.
用同样的方法将pMIT 记作Ti.pMIT 范围是pITTji,j,并且Tji≥Ti,j.
一个任务τi可以用二元组(Ci,Ti)表示.一个任务的某个作业需要在下一个作业到达之前完成执行,即新作业的到来代表着当前作业的截止时间.所以,一个任务也可以用一个随机变量Di表示,和pMIT 的Ti有一样的作用.
通过考虑最坏情况的概率值(pMIT 或pWCET),用随机的独立变量来表达pMIT 和pWCET[7].这种独立性是因为pMIT 和pWCET是边界而不是任务执行的确切值.由这个独立的性质,利用卷积计算任务的响应时间等.
任务的响应时间是从激活到执行结束的时间.作业有pET,因此响应时间也可以用随机变量来描述.
约束条件用错过截止时间的概率描述,作业τi,j的失败概率DMPi,j是指任务τi的第j个作业错过截止时间的概率,即
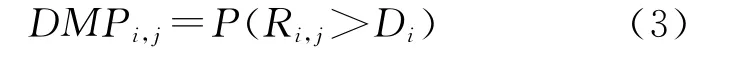
Ri,j是任务τi的第j个作业的响应时间的分布.
如果有计划的任务是周期性的,换句话说pMIT 分布有一个概率值1,然后任务失败的概率可以计算为作业的平均失败概率,这些作业在时间段[a,b]内被执行,这就是调度的超周期.一个最坏情况的推论只能考虑所有执行在时间段[a,b]所有作业的DMP中最大的DMP(失败概率).
对于一个任务τi和一个时间段[a,b],任务的失败概率可以计算为
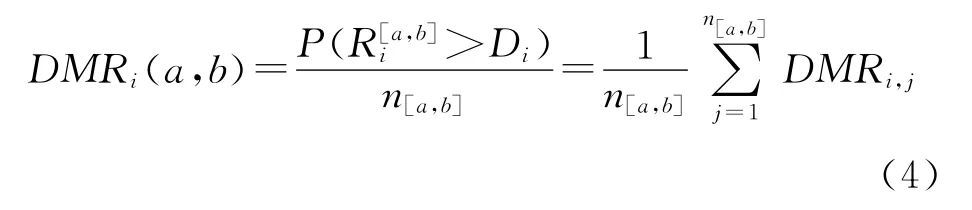
n是活跃在时间段[a,b]一个任务作业τi的作业的数量.
2 随机调度算法改进
2.1 单调速率算法概述
(1)任务τi(Ti,Ci,Di)模型
Ti为任务i的周期,Ci为任务执 行时间,Di为截止时间且为周期终点.任务在周期的起点释放,高优先级任务可以抢占低优先级任务.
(2)优先级分配方法
即静态固定优先级分配.利用线性关系优先级与周期成反比,周期越短优先级越高.
(3)可调度性分析
n个独立的周期任务组成的任务集τ可以被单调速率算法调度,如果U≤n(21/n-1),则该任务集可调度.其中U为实时系统周期任务集的负载
在静态调度中,首先提出任务的临界时刻(critical instant)的概念.定义其为一个特定时间点,如果在此时刻有任务提出请求,那么此任务就需要最大响应时间(最坏情况).
性质1 一个任务的临界时刻就是所有比此任务优先级高的任务hp(i)同时发出请求的时刻.
上述的价值在于它找到了一个调度算法在任何情况下(包括最坏情况),能否调度任一任务集的充分必要条件,即为在所有任务同时请求执行的情况下仍能保证每个任务满足相对截止时间(时限)完成任务,那么就可以用这个调度算法来对这个任务集进行调度.
性质2 如果一个任务集能够被静态调度,那么就能够用单调速率调度算法调度这个任务集.
单调速率调度算法已证明是静态最优调度算法,开销小,灵活性好,是实时调度的基础性理论.即使出现特殊情况如系统瞬时过载,也可前瞻定位丢失时限的任务.缺点是处理器利用率较低,因此对于许多复杂任务实时应用有很大的限制.
2.2 调度算法改进
2.2.1 随机实时调度 本节将呈现单处理器上固定优先调度算法的结果.此处研究的任务有单一的参数,用一个随机变量表达,即Ci.考虑有n个任务的集合τi,i∈{1,2,…,n},用(Ci,Ti,Di,p)表示,p∈[0,1]表示任务τi错过它的截止时间的最大概率.在第一个超周期[0,P]来研究调度,P=lcm{T1,T2,…,Tn}.
固定优先级调度算法问题(BPAP),需要为每个任务分配优先级,每项任务的DMR不能超过临界值,即DMRi(Φ)≤pi.
定理1 系统τ={τ1,…,τn}有n个同时释放的任务且有pWCET.对于这个系统,单调速率(RM)不是最优的,因为有一个可行的任务优先级分配,但是单调速率不一定能做到此情况下的优先级分配.
证明 设τ={τ1,τ2}是一个有两个周期性任务及pWCET 的系统.把τ1和τ2分别设定为作业τ1需要满足至少截止时间的50%,作业τ2为75%.
根据RM 优先级分配算法,τ1有最高的优先级,τ2有最低的优先级.假若这样,τ1将会满足所有它的截止时间,显然也满足要求的50%的限度.然而,τ2将不能满足截止时间的75%,只有50%(图1).
因为优先级的不同引起响应时间不同,并且调整优先级后满足截止时间的概率改变,从而产生优先级分配策略的影响,检验单调速率算法在特殊情况的最优性是否还存在.现在考虑作业τ2有最高优先级,作业τ1有最低优先级,然后两个任务都能满足它们各自的限制要求.这样的话,τ2满足它的截止时间的概率为100%(高于要求的75%),τ1将满足截止时间的50%(图2).
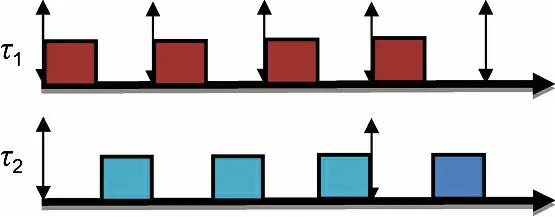
图1 单调速率调度算法调度结果Fig.1 Rate monotonic scheduling result
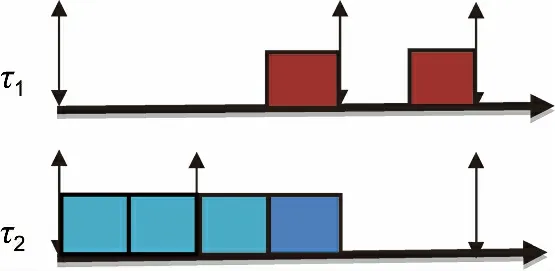
图2 合适的优先级调度策略Fig.2 A feasible assignment of priorities
引理1(最高级的顺序定理[8]) 设τ={τ1,…,τn}是n个任务的任务集并且用pWCET来约束,任务在一个用固定优先级抢占调度策略的单处理器上调度.如果任务有固定和已知的优先级,那么比τi更高优先级的任务集hp(i)的内部顺序不影响任务τi的任何作业j的DMPi,j(Φ)的值且不影响DMRi(a,b,Φ),a,b的值.
2.2.2 随机调度系统优先级算法 由于技术发展,系统很少可能错过截止时间,时间约束不再合适,所以没有必要设置一个系统功能数量的低界限,而是进行随机分析.
引理2(响应时间的单调性) 在某一个任务分配Φ中降低某一任务τi的优先级,其响应时间会增大.优先级越低,来自高优先级的冲突越多,响应时间越长,错过截止时间概率越大.
基本优先级分配问题最优算法[8]:令Γ是一个截止时间限制的任务集,任务有随机执行时间并且表示为(Ci,Ti,Di,p).对于任何任务集Γ,总能找到一个切实可行并且存在的优先级分配方案.
在基本优先级分配贪心算法上进行一些改进.从最低等级的任务开始分配优先级,直到最高级.当给任务τi设定了某一个优先级,不必担心已经被设定了更低优先级的任务集lp(i),因为这不影响τi的响应时间(引理1).
现在提出改进的算法.
基本的优先级分配最优算法:使得所有的任务τi满足DMRi≤pi

改进的地方是将待分配的任务按照最坏失败概率也就是按照pi的值进行从大到小排序,根据引理2如果最坏DMR越小则需要将任务的优先级分配得越高,这样可以减少由于贪心算法导致的中途分配失败的情况,从而提高算法的分配速度.
这个算法是贪心算法.可能存在一个未分配优先级的任务τ,如果分配当前优先级k不会让最差的DMR更差,也就是不超过pi,就把优先级k分配给此任务,而不考虑高优先级会发生的情况.这个算法在解决当前优先级固定分配问题上效率比较高,对每一个任务都进行检测,若适合就分配优先级.而如果所有任务都不满足某一优先级的条件,那么该优先级分配失败.
2.2.3 可调度性分析 考虑一个具有n个同步释放的任务的任务集{τ1,τ2,…,τn},在单处理器上使用固定任务优先级的抢占调度策略.不失一般性地,当i<j时,认为τi比τj有更高的优先级,任务τn在被研究的n个任务中具有最低的优先级.
任务τi,j的响应时间Ri,j可由下面的公式计算得出:
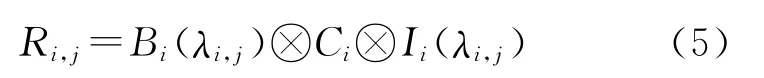
Bi(λi,j)是在λi,j之前释放的具有较高优先级的任务累积和,并且在λi,j时刻尚未终止执行.Ii(λi,j)是在λi,j之后到达的并且可以抢占任务τi,j的较高优先级的任务的最坏情况的执行时间pWCET 的累积和.在同时释放任务的情况下,这些任务pWCET 的累积和为
式(5)可以进行迭代求解,新的抢占任务的整合是通过修改任务在每个新迭代的概率分布解决的.当没有更多的抢占任务或者任务的完成时间已经大于最后完成时间时,迭代终止.
式(5)基于卷积运算,这要求任务变量Ci,i在概率上相互独立.
pET 的情况:如果随机变量Ci描述任务的pET,随机变量不能独立,在这种情况下,任务的当前状态不能使用式(5)来解决.
pWCET 的情况:如果随机变量Ci描述任务τi的pWCET,随机变量是独立的,因为它们是pET 的范围,所以式(5)是可用的.
考虑之前的例子,τ={τ1,τ2}是一个有两个周期性任务及pWCET 的系统,把τ1、τ2分别设定为
当任务τ2的优先级低于τ1时,使用式(5)计算第二个任务τ2的第一个作业τ2,1的响应时间,R2,1=B2(λ2,1)C2I2(λ2,1),其 中λ2,1=0,I2(0).当I2(0)任务τ1可能的3个值:τ1,2在t=2,τ1,3在t=4,τ1,4在t=6 时,代入得到R2,1=
3 任务调度算法仿真
本章将对基于随机模型提出的改进的固定优先级分配算法的正确性和有效性进行仿真验证.实验设定了多个具有代表性的实验用例(仅举1例),多角度全面进行仿真,并将结果与传统算法进行对比,总结分析改进算法的性能.
实验用例1Γ={τ1,τ2},

仿真结果显示,τ2优先级最高,其次为τ1,DMR2=0,明显小于0.1,DMR1=0.387 5,且小于0.5,符合要求,算法结果正确.
下面分析实验用例1,如果用单调速率算法,T1<T2,所以τ1的优先级比τ2的高,按照这个优先级分配算法来计算DMR.τ1的每个任务响应时间都为因此得出两个计算结果:即R2=所以DMR2=0.125>0.1.因此这种优先级分配算法不可行,不符合优先级分配算法的基本要求,同时也证明了单调速率算法在这种任务模型的非最优性.
4 结 语
本文研究了目前已有的任务调度和优先级分配理论,在分析了传统算法的缺点和任务调度问题的随机性与动态性之后改进了固定优先级分配算法并进行了仿真实验和性能比较,分析出本算法的优越性.
[1] 任丰原,黄海宁,林 闯.无线传感器网络[J].软件学报,2003,14(7):1282-1291.REN Feng-yuan,HUANG Hai-ning,LIN Chuang.Wireless sensor networks[J].Journal of Software,2003,14(7):1282-1291.(in Chinese)
[2] Park H,Srivastava M B.Energy-efficient task assignment framework for wireless sensor networks[R].Los Angeles:Center for Embedded Network Sensing,University of California,2003.
[3] 吴光斌,梁长垠.无线传感器网络能量有效性的研究[J].传感器技术,2004,23(7):74-76.WU Guang-bin,LIANG Chang-yin.Research of energy-efficiency for wireless sensor networks[J].Journal of Transducer Technology,2004,23(7):74-76.(in Chinese)
[4] Liu C L,Layland J W.Scheduling algorithms for multiprogramming in a hard real-time environment[J].Journal of the ACM,1973,20(1):46-61.
[5] 郭文忠.无线传感器网络任务调度若干关键技术研究[D].福州:福州大学,2010:4-8.GUO Wen-zhong.Research on some key technology of task scheduling in wireless sensor networks[D].Fuzhou:Fuzhou University,2010:4-8.(in Chinese)
[6] Mok A.Fundamental design problems of distributed systems for the hard-real-time environment[D].Boston:Laboratory for Computer Science,Massachusetts Institute of Technology,1983:35-54.
[7] Stappert F,Altenbernd P.Complete worst-case execution time analysis of straight-line hard realtime programs[J].Journal of Systems Architecture,2000,46(4):339-355.
[8] Maxim D,Buffet O,Santinelli L,etal.Optimal priority assignments for probabilistic real-time systems[C]//Proceeding of the 19th International Conference on Real-Time and Network Systems(RTNS).Nantes:IEEE Computer Society,2011:2-8.

