基于四阶累积量的近场源多参数联合估计
王 鹏,邱天爽*,李景春,谭海峰,3
(1.大连理工大学 电子信息与电气工程学部,辽宁 大连 116024;2.国家无线电监测中心,北京 100037;3.北京邮电大学 信息与通信工程学院,北京 100876)
0 引 言
空间信源的位置估计是阵列信号处理与应用中的基本问题之一,也是声呐、雷达、地震探测以及电子侦察等领域的重要任务之一.根据信源与阵列天线的位置关系,可以将空间信源分为远场源和近场源.在传播过程中,远场源的波前可以用平面波进行描述,其位置可由单一的波达方向(direction of arrival,DOA)给出,然而当信源靠近菲涅尔区即近场情况下,此时电磁传播过程中的波前曲率不可忽略,必须采用球面波进行描述,其位置则需利用距离和DOA 进行联合确定.
针对近场源的参数估计问题,文献[1]提出了最大似然估计法,文献[2]提出将1D-MUSIC 算法扩展为2D-MUSIC方法,以实现近场源的位置估计,但需要进行二维峰值搜索.为了减小计算量,学者们相继提出了Root-MUSIC 方 法[3]、路径跟踪算法[4]以及CA-MUSIC 方法[5]等多种方法,但仍需进行多次一维峰值搜索,计算量十分可观.为此,学者们进一步提出了无须峰值搜索的方法[6-16],其中以Challa等[9]和Yuen等[10]为代表提出的ESPRIT-like方法[9-16]最受关注,该方法通过构造合适的累积量矩阵并采用子空间旋转不变技术进行信源参数的估计,具有封闭的数学表达式,不需要任何峰值搜索,而且高阶累积量对高斯噪声具有鲁棒性,因此该类算法适用于任意形式的高斯噪声环境.
文献[9-12]提出了多个近场窄带信源的方位与距离的联合估计方法,但该类方法假设多个信源具有相同载频且频率已知,不适用于载频不同且未知电磁环境.针对这一不足,文献[13-16]提出了近场窄带信源频率、方位以及距离三维参数的联合估计方法,取得较好效果的同时也存在一定的不足,主要体现在两个方面:一是采用中心对称接收阵列的方法损失了部分阵列孔径,参数估计分辨能力低;二是采用非中心对称接收阵列的方法提高了孔径利用率,却需要构造多个累积量矩阵,计算量较大.为弥补以上不足,本文提出一种改进的近场窄带多信源参数估计方法,通过所构造四阶累积量矩阵的特征分解实现DOA、频率以及距离参数的联合估计.
1 信号模型
假设空间存在P个近场窄带信源,入射到一个阵元个数为M的均匀线阵(见图1),阵元间距为d,接收到的信号经过下变频至中频并以采样频率fs进行抽样,当以阵元0为参考阵元时,第m个阵元上的接收数据可以表示为

图1 均匀线阵结构图Fig.1 Uniform linear sensor array configuration

式中:K是快拍数;wm(k)为第m个接收阵元的噪声;ωi=2πfi/fs,是第i个信源的数字频率;τmi是第i个信源在阵元m相对参考阵元相位差,由信源位置(ri,θi)唯一确定[1].
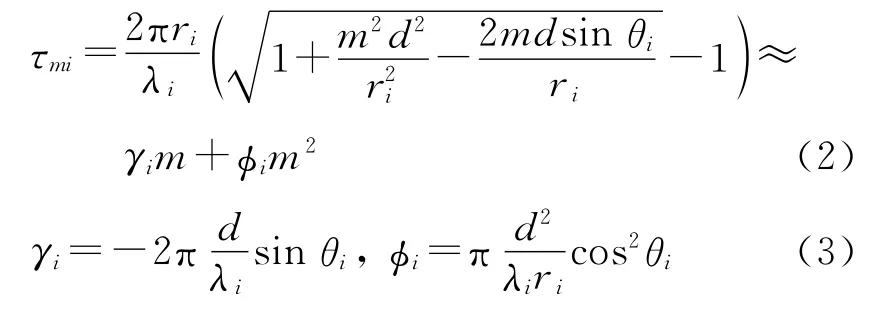
其中ri表示第i个信源到参考阵元的距离,θi和λi分别表示第i个信源的入射角以及波长.为了简化信号模型,本文作如下假设:
(1)信源为窄带平稳随机过程,满足均值为零,峰度值非零,且信源之间相互独立;
(2)噪声为高斯过程,满足均值为零,阵元间噪声以及噪声与信源之间相互独立;
(3)对于不同的信源i≠j,满足ωi≠ωj,γi≠γj,≠;
(4)阵元间距d≤min(λi)/4,信源个数已知并满足P<M.
2 三维参数联合估计方法
定义大小为M×M的四阶累积量矩阵C1,形式如下:

将式(1)代入式(4),在假设(1)和(2)下,结合四阶累积量的性质[17]可以得到

对于-1≤m,n≤M-2,可以将式(5)写成矩阵形式:

其中C4s=diag{c4s1,c4s2,…,c4sP},是以信源峰度值c4si为对角元素的矩阵;A是大小为M×P的阵列流形,其第i列称为导向矢量,可以表示为

在窄带假设条件下,有si(k+1)≈si(k)成立,经过推导得到两个新的累积量矩阵C2、C3:
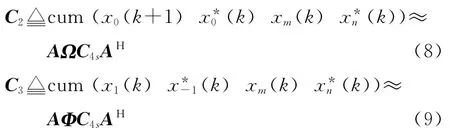
式中:Ω=diag{ejω1,ejω2,…,ejωP},Φ=diag{ej2γ1,ej2γ2,…,ej2γP}.
由假设条件(1)和(3)可知,矩阵C1列满秩且秩为P,对其进行特征分解得到

M个特征值满足ρ1≥ρ2≥…≥ρP>ρP+1=…=ρM=0,ui是第i个特征值对应的特征向量.
定义矩阵C1的伪逆C#1为

经过数学推导[13]可以得到

由假设(1)和(3)可知,矩阵A和Ω分别为列满秩矩阵和可逆对角阵.对矩阵C2C#1进行特征分解得到的P个非零特征值就对应着ejω1,ejω2,…,ejωP.
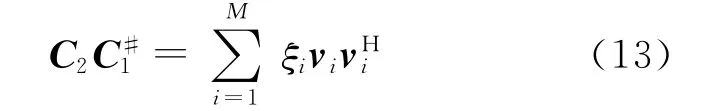
通过下式可以得到数字频率的估计:
angle(·) 表示对“·”求辐角.对累积量矩阵C3进行相似的处理可以得到

同样地,对C3C#1进行特征分解得到的P个非零特征值对应ej2γ1,ej2γ2,…,ej2γP.

通过下式可以得到γi的估计为

通过特征值对应的特征向量就可以得到的估计
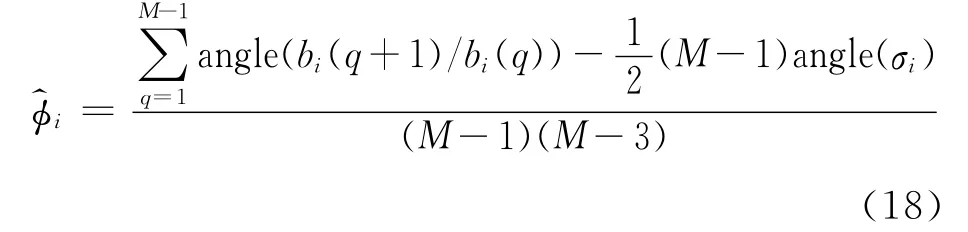

综上,可以得到近场窄带信源的频率、方向以及距离的三维参数估计为
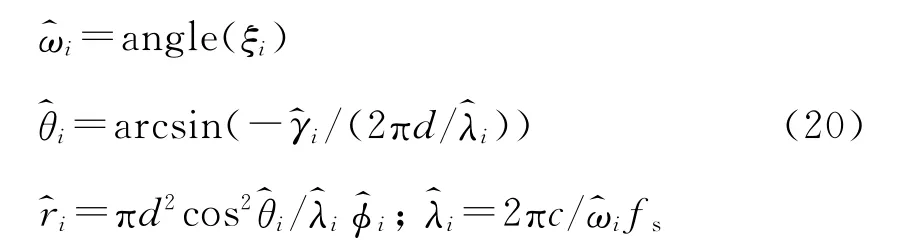
其中c为电磁波的传播速度和分别由式(17)和(18)估计得到.
假设本文所用接收阵列由M个阵元组成,M为偶数,文献[13-14]采用中心对称结构,由接收数据所构造的高阶累积量矩阵大小是(M/2)×(M/2),有M/2个阵元孔径的损失,最多可估计M/2-1个信源.本文和文献[15-16]采用非中心对称结构,由接收数据所构造的累积量矩阵维数是M×M,避免了阵列天线的孔径损失,最多可估计M-1个信源.
由于四阶累积量矩阵的构造以及矩阵的特征分解是算法运算复杂度的主要体现,本文主要考虑这两项的计算复杂度.利用快拍数为K的接收数据构造一个大小为M×M高阶累积量矩阵的计算复杂度为O(9M2K),对其进行特征分解的计算复杂度为O(4M3/3).本文方法共需要构造3个M×M高阶累积量矩阵,并需要3 次特征分解,所以计算复杂度为O(27M2K+4M3),低于采用同样结构的文献[15]和[16],其计算复杂度分别 为O(36M2K+272M3/3)和O(54M2K+72M3).在参数配对方面,本文方法需要一次参数配对,文献[15]需要进行两次参数配对,而文献[16]则不需要参数配对.
3 仿真实验
考虑一个阵元数目M=8的均匀线阵,阵元间距d=min(λi)/4,空间存在两个等功率且统计独立的近场窄带信源,中心频率分别为f1=3 MHz,f2=4 MHz.仿真实验中采样频率为10 MHz,本文以均方根误差erms作为方法性能的评价准则,结果由L=300次独立实验统计得到:
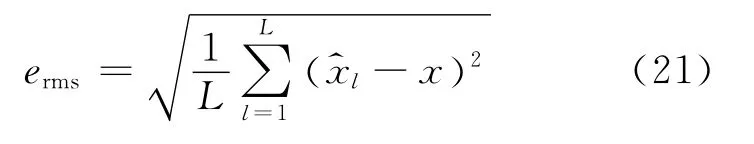
其中代表本文方法得到的参数估计值,x代表参数的真值.
实验1 比较本文方法与文献[14-16]方法在不同信噪比下的近场源参数估计性能,其中信噪比Rsn从0dB到25dB变化,数据长度为2 000个快拍,入射角度分别为θ1=-15°,θ2=30°,到参考阵元的距离分别为r1=1.5λ1,r2=0.8λ2.
图2给出了不同Rsn下不同方法参数估计erms的变化曲线.从图中可以看出,在频率估计方面,本文方法的性能比文献[16]方法略差,与文献[15]方法估计性能相当,明显优于文献[14]方法.这是因为文献[14]方法采用了中心对称结构阵列,具有较大的孔径损失而导致各参数估计性能都比较低.相比于文献[16]方法,本文构造高阶累积量矩阵个数少,估计频率所用的高阶累积量矩阵维数小,因而频率估计性能略差.在到达角估计方面,本文方法与文献[15]方法估计性能基本相同,略优于文献[16]方法,明显优于文献[14]方法.而在距离估计方面,本文方法则明显优于文献[14-16]中的方法.
实验2 比较本文方法与文献[14-16]方法在不同快拍数下的参数估计性能,其中信噪比Rsn固定为20dB,数据长度范围为500 到2 500个快拍,入射角度分别为θ1=-15°,θ2=30°,到参考阵元的距离分别为r1=1.5λ1,r2=0.8λ2.
图3给出了不同快拍数下参数估计erms的变化曲线.从图中可以看出,各方法性能随快拍数的增加而提高,方法之间的性能比较结果与实验1结论相同:本文方法除在频率估计性能略差于文献[16]方法以外,其他两个参数都能取得比其他方法更加精确的估计结果.此外,由实验1和实验2的结果还可以发现,位置较近信源的距离参数估计精度明显高于位置较远信源的参数估计结果,这与文献[10]的理论分析是一致的,说明了本文方法的有效性.
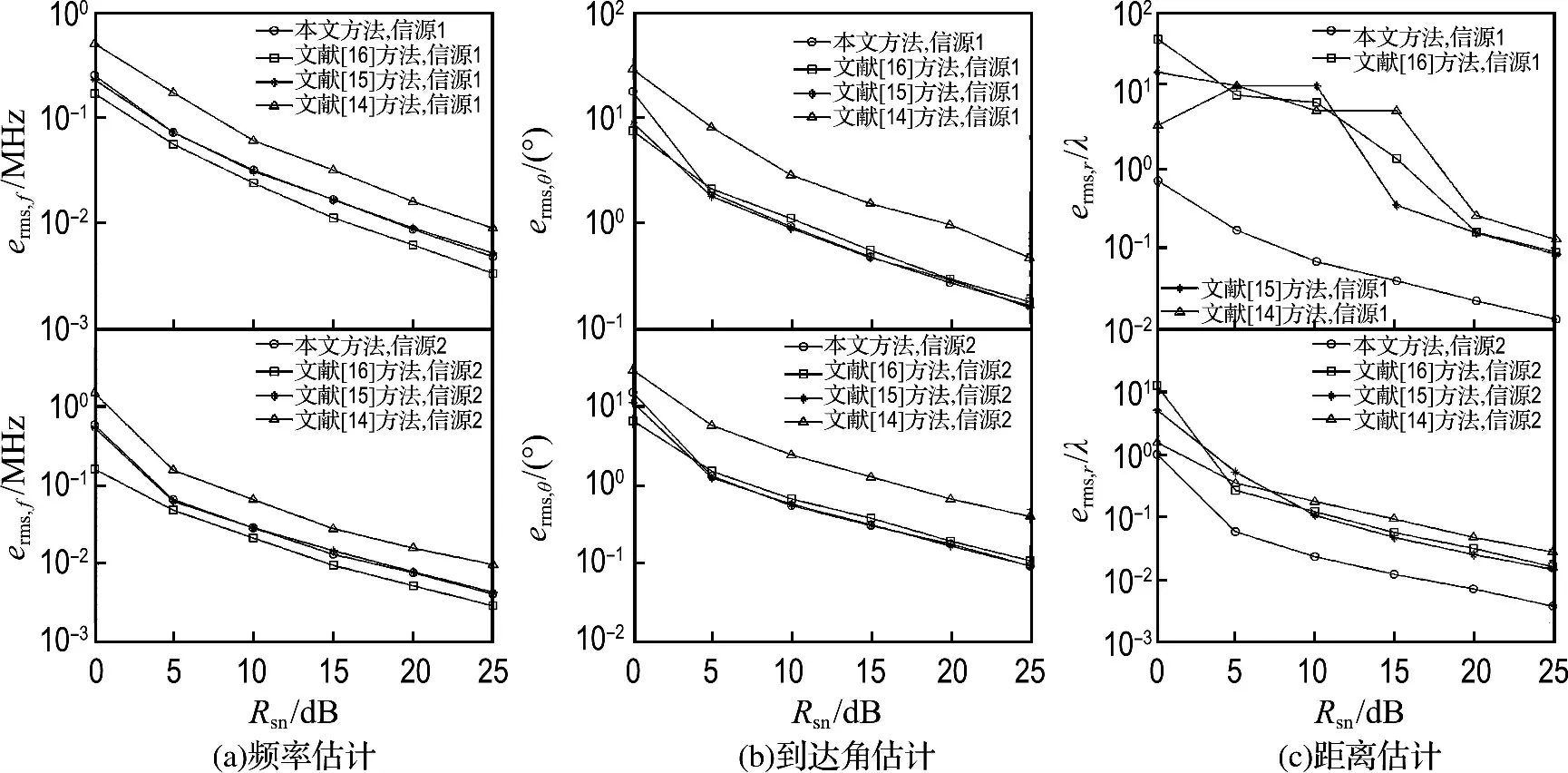
图2 不同信噪比下的近场源参数估计误差Fig.2 Errors of parameters estimation for near-field sources under different SNR
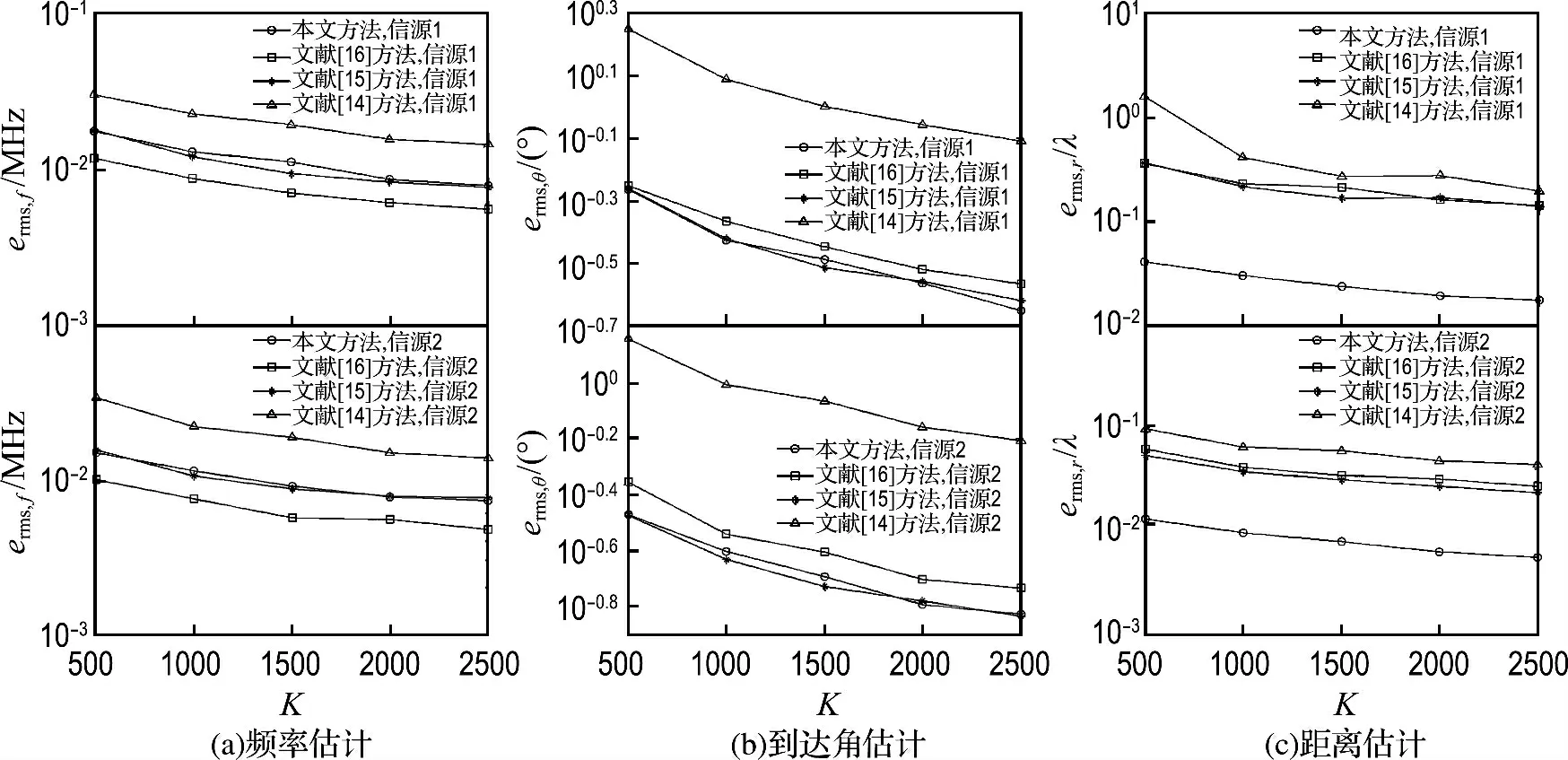
图3 不同快拍数下的近场源参数估计误差Fig.3 Errors of parameters estimation for near-field sources under different snapshots
实验3 比较本文方法与文献[14-16]方法在不同入射角下的参数估计性能.其中,信噪比固定为20dB,信源1入射角θ1从0°变化至30°,信源2入射角固定为θ2=30°,到参考阵元的距离分别为r1=1.5λ1,r2=0.8λ2.
图4给出了不同入射角下的参数估计erms变化曲线.从图中可以看出,随着信源1入射方向的变化,各信源参数估计性能与实验1和实验2中的结论是一致的.此外还可以发现,在距离和频率不同的情况下,同一方向的两个信源是可以分离的.需要指出的是,本文方法和文献[14]方法的距离参数估计误差会随着两个信源入射方向的接近而增大.
实验4 比较本文方法与文献[14-16]方法在不同距离下的参数估计性能.其中,信噪比固定为20dB,信源1的入射角θ1=-15°,信源2的入射角θ2=30°,到参考阵元的距离分别为r1从0.5λ1变化至4λ1,r2=0.8λ2.
图5给出了不同距离参数下的erms变化曲线.除文献[14]方法以外,其余方法的频率估计、到达角估计以及信源2的距离估计erms随信源1距离的增大没有明显的变化,而信源1的距离估计erms则随距离的增大而增大.文献[14]方法在r1=0.5λ1时参数估计误差较大,这是因为此时两信源的距离参数几乎相等,不能充分保证文献[14]方法中要求两者距离参数不相等的假设.
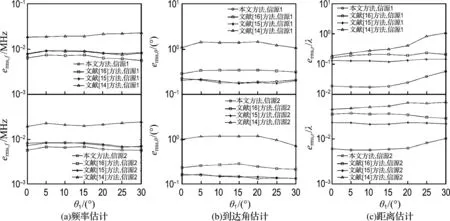
图4 不同信源1入射角下近场源参数估计误差Fig.4 Errors of parameters estimation for near-field sources under different DOAs of source 1

图5 不同距离下近场源参数估计误差Fig.5 Errors of parameters estimation for near-field sources under different ranges
实验5 比较本文方法与文献[15-16]方法的复杂度,信噪比固定为20dB,数据长度范围为500到2 500个快拍,统计300次Monte-Carlo实验的运行时间.
表1给出了相同条件下不同方法的运行时间,从表中可以看出,文献[16]方法运行时间约为本文方法的1.8倍,文献[15]方法运行时间约为本文方法的1.3倍,与理论分析是一致的,说明本文方法具有更低的运算复杂度.
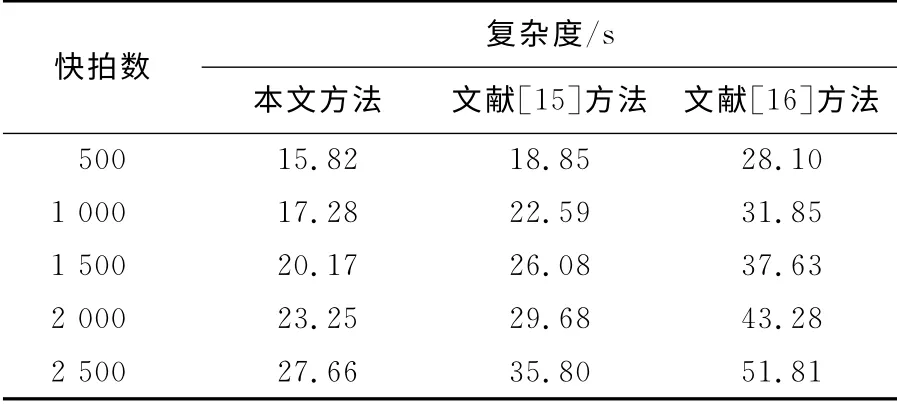
表1 不同方法运算复杂度比较Tab.1 Comparison of computational complexity for different methods
4 结 语
本文提出了一种改进的近场窄带信源多参数估计方法,能够实现多信源的频率、距离以及DOA 的联合估计.通过采用非对称阵列结构以达到避免阵列孔径损失的目的,通过构造新的累积量矩阵以达到降低算法的计算复杂度的效果.最后,仿真实验结果表明,本文方法除在频率估计精度方面略低于文献[16]方法外,其他两个参数的估计精度均高于其他方法,尤其是距离参数估计精度明显高于其他方法,证明了本文方法的有效性.此外,本文方法在保证参数估计精度的同时,有效地缩短了运行时间,说明了本文方法的工程应用价值.
[1] Kailath T,Swindlehurst A L.Passive direction-ofarrival and range estimation for near-field sources[C]//Fourth Annual ASSP Workshop on Spectrum Estimation and Modeling.Piscataway:IEEE,1988:123-128.
[2] Jeffers R,Bell K L,Van Trees H L.Broadband passive range estimation using MUSIC [J].ICASSP,IEEE International Conference on Acoustics,Speech and Signal Processing -Proceedings,2002,3:2921-2924.
[3] Weiss A J,Friedlander B.Range and bearing estimation using polynomial rooting [J].IEEE Journal of Oceanic Engineering,1993,18(2):130-137.
[4] Starer D,Nehorai A.Passive localization on nearfield sources by path following [J].IEEE Transactions on Signal Processing,1994,42(3):677-680.
[5] Noh H,Lee C Y.A covariance approximation method for near-field coherent sources localization using uniform linear array [J].IEEE Journal of Oceanic Engineering,2015,40(1):187-195.
[6] Gazzah H,Delmas J P.CRB-based design of linear antenna arrays for near-field source localization[J].IEEE Transactions on Antennas and Propagation,2014,62(4):1965-1974.
[7] CHEN Jian,LIU Guo-hong,SUN Xiao-ying.Computationally efficient near-field source localization using third-order moments [J].EURASIP Journal on Advances in Signal Processing,2014,2014(1):1-8.
[8] 王 超,魏玺章.基于联合对角化的近场源三维参数估计[J].雷达科学与技术,2014,12(1):63-68,75.WANG Chao,WEI Xi-zhang.Estimating 3-D parameters of near-field sources based joint diagonalization[J].Radar Science and Technology,2014,12(1):63-68,75.(in Chinese)
[9] Challa R N,Shamsunder S.High-order subspacebased algorithms for passive localization of nearfield sources [C]//The Twenty-Ninth Asilomar Conference on Signals,Systems and Computers(Volume:2).Los Alamitos:IEEE Computer Society Press,1995:777-781.
[10] Yuen N,Friedlander B.Performance analysis of higher order ESPRIT for localization of near-field sources [J].IEEE Transactions on Signal Processing,1998,46(3):709-719.
[11] WU Yun-tao,MA Lin,HOU Chao-huan,etal.Subspace-based method for joint range and DOA estimation of multiple near-field sources[J].Signal Processing,2006,86(8):2129-2133.
[12] 梁军利,刘 丁,张军英.基于ESPRIT 方法的近场源参数估计[J].系统工程与电子技术,2009,31(6):1299-1302.LIANG Jun-li,LIU Ding,ZHANG Jun-ying.New ESPRIT approach to near-field source parameter estimation[J].Systems Engineering and Electronics,2009,31(6):1299-1302.(in Chinese)
[13] 马克江,李 军,吴云韬,等.无需参数配对的近场源距离、方位、频率联合估计算法[J].电子学报,2010,38(6):1454-1458.MA Ke-jiang,LI Jun,WU Yun-tao,etal.Joint ranges DOA′s and frequencies estimation of nearfield sources without pairing parameters[J].Acta Electronica Sinica,2010,38(6):1454-1458.(in Chinese)
[14] 陈建峰,张贤达,吴云韬.近场源距离、频率及到达角联合估计算法[J].电子学报,2004,32(5):803-806.CHEN Jian-feng,ZHANG Xian-da,WU Yun-tao.An algorithm for jointly estimating range DOA and frequency of near field source[J].Acta Electronica Sinica,2004,32(5):803-806.(in Chinese)
[15] 吴云韬,侯朝焕,王 荣,等.一种基于高阶累积量的近场源距离、频率和方位联合估计算法[J].电子学报,2005,33(10):1893-1896.WU Yun-tao,HOU Chao-huan,WANG Rong,etal.Joint ranges DOA′s and frequencies estimation of multiple near-field sources using cumulant [J].Acta Electronica Sinica,2005,33(10):1893-1896.(in Chinese)
[16] 马克江,李 军,吴云韬,等.基于累量域的近场源三维参数联合估计算法[J].系统工程与电子技术,2010,32(10):2041-2044.MA Ke-jiang,LI Jun,WU Yun-tao,etal.Joint estimative method of three-dimensional parameters for near-field sources based on cumulant [J].Systems Engineering and Electronics,2010,32(10):2041-2044.(in Chinese)
[17] Mendel J M.Tutorial on higher-order statistics(spectra)in signal processing and system theory:Theoretical results and some applications [J].Proceedings of the IEEE,1991,79(3):278-305.

