有限差分法在电厂地下结构设计中的应用

商金华，张兰春，徐俊祥

(山东电力工程咨询院有限公司，山东 济南 250013)

1 研究现状和意义

1.1 研究现状

地下结构的受力分析与土力学的发展密不可分。土力学的发展起步较晚，与弹性力学、材料力学等其他固体力学发展历史相比，相对滞后。土体与地下结构的相互作用是近期才被频繁提及的新问题。伴随地下空间开发规模越来越大，为了适应工程实际的需要，一些地下结构分析的理论和方法开始逐渐出现，主要可分为以下几种：解析法；半解析法；数值方法；模型试验。

近年来，伴随试验条件的进步和计算理论的完善，国内外工程技术员在地下结构模型试验、土的工程性质、地基 与地下结构分析等方面都有广泛研究，并取得了大量成果。就目前而言，一般是通过原位试验和模型试验相结合，建立合理的数理分析模型，发展相应的数值分析方法，然后针对不同设计方案进行计算分析，再现工程中结构的内力分布，研究结构性能。这是计算和分析地下结构受力特性有效、便捷的途径。

1.2 目的和意义

火力发电是我国现阶段电力能源供给的主要方式，火力发电量占全部发电量的80%左右。而火力发电中几乎全部都是燃煤发电，其他形式的热源所占比例极小。

煤的输送是火力发电中非常重要的一个环节。火力发电厂中输煤的主要结构是输煤栈桥和输煤转运站。实际工程中，由于输煤工艺的需要，起始段的输煤结构的标高低于室外地坪，形成掩埋于地下的转运站和输煤廊道，已有埋深超过20m的工程实例。电厂输煤系统中的各组成部分是串联形式，任何一个环节发生破坏，都将导致电厂无法正常生产。因此，地下转运站和输煤廊道等地下结构的安全性十分重要。

地下结构的受力分析研究起步较晚。现阶段工程设计中，通常的做法是借鉴地上结构的计算方法，采用荷载－结构法，即将周围土体的作用简化为荷载作用在地下结构上。这种方法只考虑土体的重力和由重力产生的侧向土压力，将其转化为作用在结构上的竖向荷载和水平向荷载。

但由于地上结构与地下结构受力机理不同，使得这种借鉴缺乏实际意义。荷载－结构法忽视了结构周围土体的力学特性，不能反映地基土体的变形对结构内力的影响和土体与结构之间的相互作用，计算理论本身存在缺陷。是否有更加合理、与实际情况更相符的计算方法可供使用，是工程设计中亟待解决的问题。

2 有限差分法

有限差分法的基本原理是将连续的求解区域用离散点来代替，求解域上的连续变量函数用离散点上的离散变量函数近似。求解完成后，再利用插值方法获得整个连续求解域上的数值解答。

2.1 基本原理

对地下结构及其周围土体进行受力分析时，分析对象可进行简化，将多自由度体系简化为一系列单自由度体系。平衡微分方程可表达为：

式中：[M]为体系的质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵； 为体系的加速度；为速度；{u}为位移；{p}为荷载向量。

2.2 实现手段

地下结构分析中，对于边界简单、受力均匀的单构件可手工计算或编制简单程序进行辅助。对于边界复杂、荷载形式多样的多构件结构则需借助已有的程序进行计算，其中FLAC是较为常见的一种有限差分计算程序。

此类程序具有以下特点：

(1) 可采用显式算法进行方程组求解，相对于有限元方法节占用更少的存储空间。

(2) 可以全部采用动力学方法进行计算。对于静力学问题，也通过对过程的追踪，转化为动力学问题。

(3) 对材料的大变形、软化、塑性流动、塑性破坏等现象能更高效的计算。

(4) 由于采用了显式算法，能够取得研究对象全部的时间步长解，因此可以分析地下结构的坍塌和逐步破坏。

有限差分程序具有如下缺陷：

(1) 如果分析中地下结构的材料当做弹性材料，且应力应变均为线性变化时，有限差分法的计算效率将会降低。

(2) 计算过程是否收敛，收敛速度快慢，与被分析体系的最大固有周期与最小固有周期的比值有关。

2.3 计算过程

地下结构受力分析的有限差分程序，其计算过程为：

假定应力波在土体与结构中传播，速度已知。如果能将计算时间步长取得很小，使计算区域的更新速度大于应力、应变、速度、位移等力学变量的更新速度，那么就能在每个时间步长内，根据各离散点的受力状态更新其运动状态，且各单元的受力状态不发生变化。

之后，再根据运动状态得出各单元的受力状态，且在更新各离散点的受力状态时，每个单元的位移和变形保持不变。下一时间段，再把每个单元的力、应力、质量以及孔隙水渗流的作用集中在离散点上，迭代计算。

通过以上处理，便将连续介质的运动学方程转化为在离散节点处的力学方程，然后在每一时间步长内，计算求解域上的普遍偏微分方程组。

3 工程实例计算

为验证有限差分法在电厂地下结构设计中应用的可行性，对已建成结构进行内力计算，结合工程经验，分析结果的合理性。计算对象选取某国外已建成转运站，底板埋深为24 m，结构净高为15 m。

3.1 计算范围及网格划分

有研究表明，采用自由场边界时，两侧岩土介质取3倍结构宽度已可使计算结果趋于稳定。深度方面，鉴于地下工程的影响深度一般不足50 m，且地质勘测的深度一般不超过70 m，拟将计算深度取为70 m。

网格划分过程中，地基土体采用离散点模拟，地下结构构件采用梁单元模拟。计算模型的网格划分，见图1。

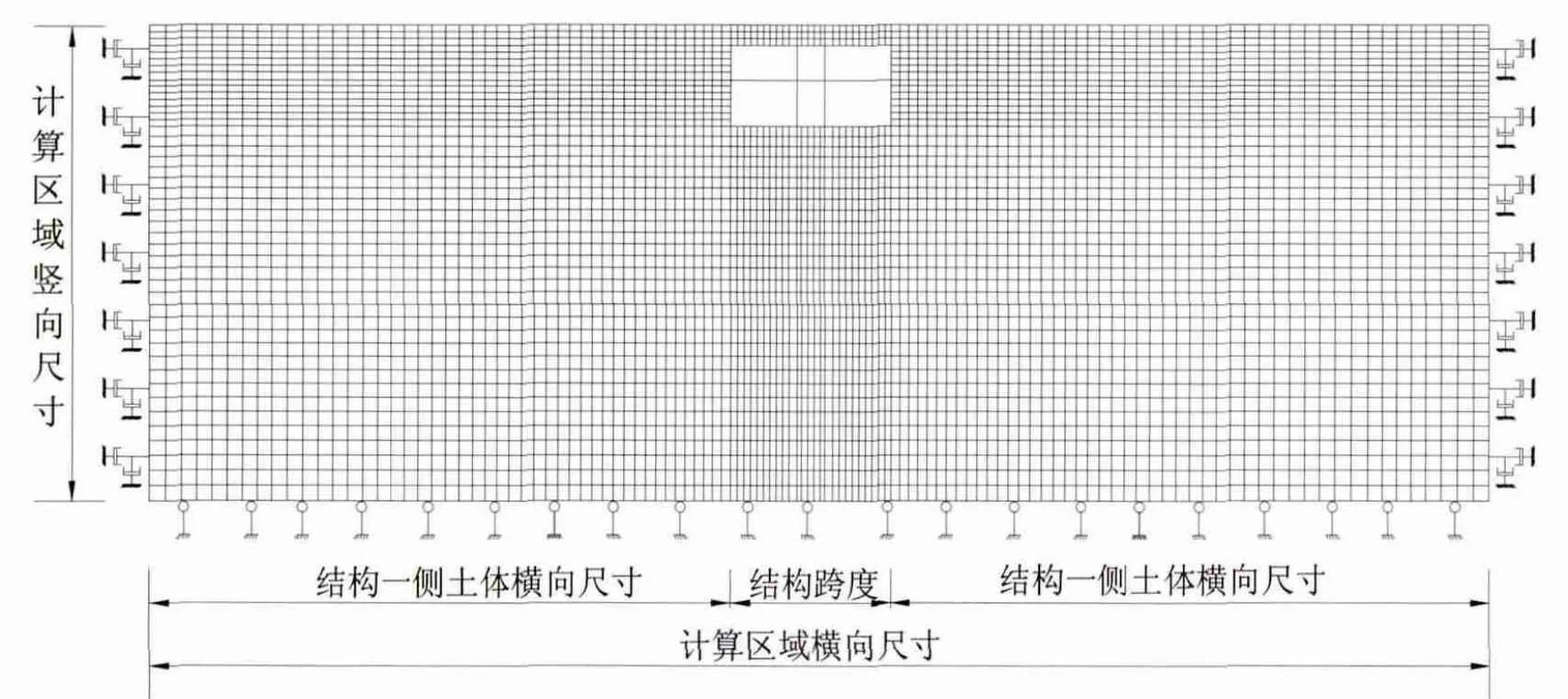
图1 计算范围示意图

3.2 材料本构模型及参数

地下转运站周围土体的地质柱状图见图2。土层物理参数见表1。

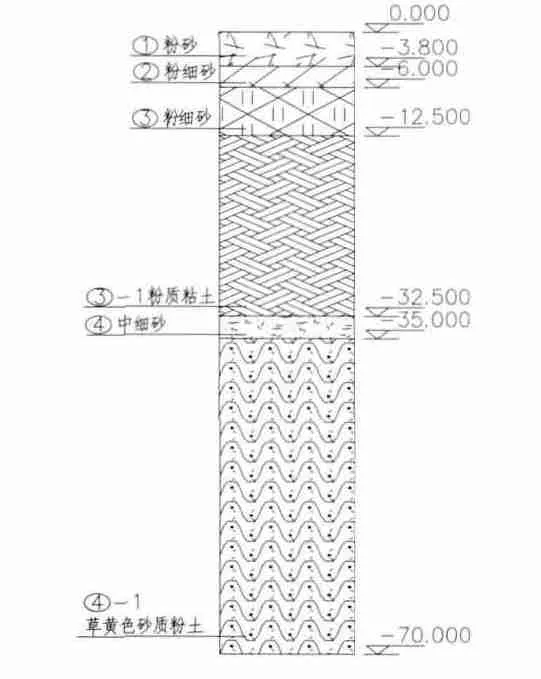
图2 地质柱状图

表1 土层物理力学性质参数

计算过程中，土体本构模型采用Mohr-Column破坏准则。当采用有效应力原理描述时，表达式为：

地下转运站均为钢筋混凝土结构，按弹性材料计算。参数可根据混凝土标号由表2取用。

表2 混凝土力学参数表

水土侧压力是影响结构内力的重要因素，不同算法对侧压力的计算方式不同。现阶段普遍的做法是采用侧压力系数法，即某一深度的水土侧压力为竖向压力与侧压力系数的乘积。在荷载—结构法中，一般取土体的侧压力系数为0.5，水的侧压力系数为1；在有限差分法中，不同程序的侧压力系数计算方法不同。本算例中取土体的侧压力系数为1－sinφ(φ为土体的内摩擦角)，水的侧压力系数为1。当各层土体的内摩擦角取值接近300时，两中算法的侧压力取值相近。

模型考虑初始地应力及开挖的影响。首先在地基土体中施加重力并计算，至土体静力平衡，形成初始地应力场；然后通过单元生死功能，“挖去”结构区域的土体结构单元，并布置结构梁、柱网格，再次进行计算至静力平衡，模拟“开挖—施工—回填”过程中土体与结构的相互作用，得到结构内力。

计算中不考虑水渗流的影响。

3.3 边界条件

两侧边界取为水平向固定、竖向自由变形的边界；底部边界为竖向固定、水平向自由变形的边界；顶部边界为自由边界。

3.4 计算结果

采用有限差分法进行地下转运站结构的受力分析，得到结构的弯矩图、剪力图、轴力图，见图3—图5。

为对比分析，采用传统的荷载—结构法，将周围土体对结构的作用简化为荷载，作用在结构上，对地下转运站进行内力计算，结果见图6—图8。

3.5 结果分析

图3 地下转运站弯矩图

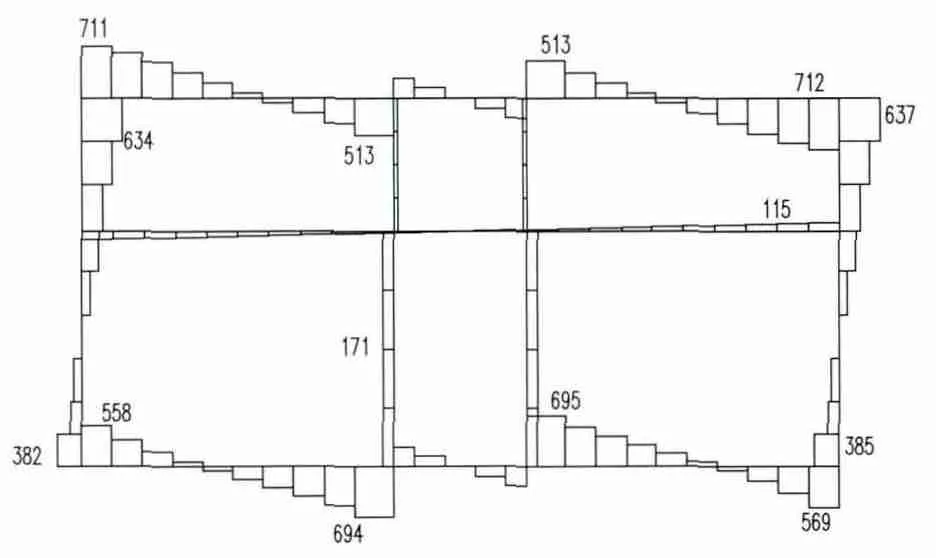
图4 地下转运站剪力图

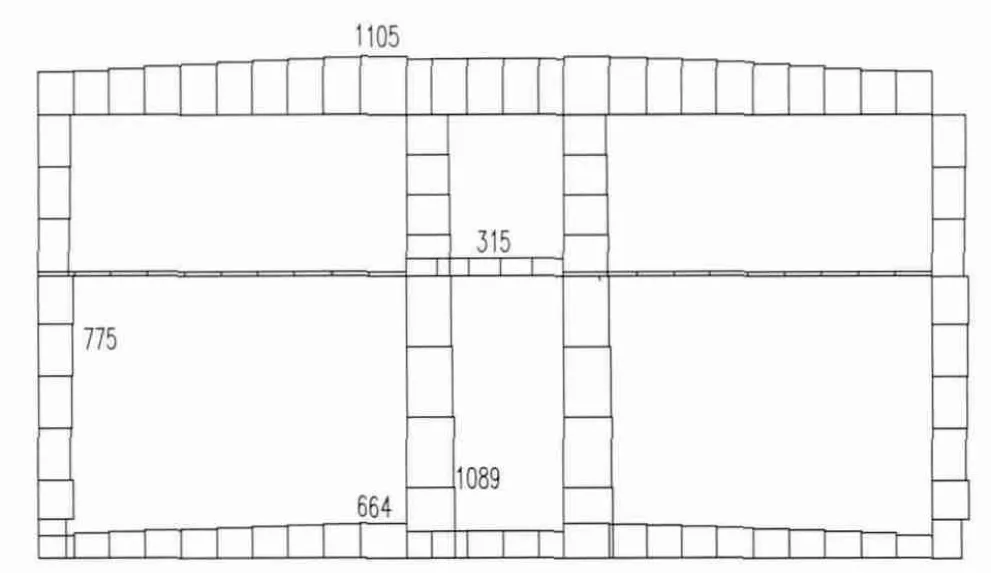
图5 地下转运站轴力图

图6 地下转运站弯矩图

图7 地下转运站剪力图

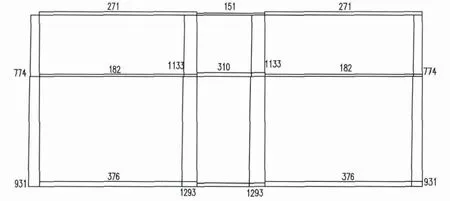
图8 地下转运站轴力图

与传统方法相比，有限差分算法的优势在于建立力学模型时将电厂地下结构与周围土体一起考虑。模型能充分反映土体的力学和变形特性以及对结构变形和内力的影响。从图3—图6可以看出，有限差分法计算所得的顶板弯矩最大值出现在顶板与侧壁结合处，而传统方法出现在顶板与中柱的结合处；有限差分法算得的底板弯矩最大值较传统方法更大。究其原因，在于有限差分法能够考虑结构和土体的真实变形：地下结构的中心沉降一般大于边缘沉降，从而造成了顶板弯矩中部变小、端部变大，而底板弯矩中部变大、端部变小的特点。比较两种算法的轴力计算结果，也可看出有限差分法更能体现土体沉降和结构位移对构件内力的影响。

在有限差分法的计算中，结构顶板和底板与周围土体共用单元网格和节点，因此，除满足内力平衡条件外，还要满足结构与土体的变形协调。而荷载—结构法只需满足内力平衡条件即可，因此两种算法的轴力计算结果差别较大。

4 结论

通过结果分析可以看出，有限差分法计算所得的构件内力控制值和内力变化趋势与工程经验相符，与实际吻合。与传统方法相比，由于有限差分法考虑了土体的力学和变形特性、土与结构的相互作用等因素，能较真实的反应土体沉降和结构变形对构件内力的影响，在分析理论上较传统方法更具说服力，是一种可供电厂地下结构设计参考使用的方法。

[1]孙钧，侯学渊．地下结构(上、下册)[M]．北京：科学出版社，1991．

[2]曹善安．地下结构力学[M]．大连：大连理工学院出版社，1986．

[3]王国波．软土地铁车站结构三维地震响应计算理论与方法的研究[D]．上海：同济大学土木学院，2007．

[4]陈仲颐，周景星，王洪瑾．土力学[M]．北京：清华大学出版社，1994．

[5]沈珠江，应变软化材料的广义孔隙压力模型[J]．岩土工程学报，1997，19(3)．

[6]DGJ08－11，地基基础设计规范[S]．