基于LS-SVM测量生物组织光学参量的实验研究
杨 丽,高美婷
(中国民航大学理学院,天津300300)
引 言
生物组织的光学特性参量能够反映组织内部结构及病理状况,因此,利用激光技术无损测量生物组织光学特性参量具有重要意义。近年来,空间分辨测量技术即通过组织表面的漫反射光分布来测量组织光学参量,得到了快速发展。参考文献[1]~参考文献[2]中采用漫射近似方法得到光学参量;参考文献[3]中WARNCKE等人利用神经网络方法,通过蒙特卡洛模拟的数据建立反演模型,获得光学参量。漫射近似理论解出的是近似值,应用于复杂结构组织时测量精度不够,且只适用于有效散射系数远大于吸收系数的介质。神经网络为机器学习方法,即在漫反射光和光学参量之间,通过训练或拟合,建立一个非线性的反演回归模型,将测得的漫反射光输入该模型,可快速得到相应的光学参量。但其预测误差较大且预测能力依赖大量的样本数据[4]。支持向量机(support vector machine,SVM)是 CORTES 和 VAPNIK[5]最初提出采用结构风险最小化原则取代经验风险最小化原则[6],具有出色的学习泛化能力,已广泛应用于各个领域[7],但在测量生物组织光学参量方面尚未可见。
最小二乘支持向量机(least squares support vector machine,LS-SVM)[8]采用最小二乘线性系统代替传统的支持向量机的二次规划方法,简化了计算过程,加快了运算速度,提高了预测准确度[9]。本文中利用CCD实验装置测量模拟液表面的漫反射光分布[10],其克服了光纤扫描方法的测量时间长、近光源区的漫反射光无法测量等不足,建立测量生物组织模拟液光学参量的LS-SVM模型,分析了漫反射光的数据长度对LSSVM模型预测精度的影响,以及LS-SVM用于小样本预测的可行性和有效性。
1 原理
对于给定的训练样本集:(x1,y1),…,(xs,ys)∈Rn×R,(i=1,2,3,…,s),最佳回归函数为:

式中,w∈Rn,b∈R,φ(x)为一种从 Rn到高维空间的非线形映射,并且满足以下的结构风险最小化:

式中,c为惩罚因子,‖w‖2控制模型的复杂度,Remp为损失函数。损失函数一般有一次损失函数、Huber损失函数及二次损失函数,不同的损失函数可构造不同形式的支持向量机[11-12]。由二次损失函数构造的支持向量机即为最小二乘支持向量机,其表达式Remp=∑iξi2,ξ是模型对训练集的训练误差[13],基于结构风险最小化原则LS-SVM的目标优化函数为:

约束条件为:yi=φ(xi)w+b+ξi,i=1,…,l。
为求解上述问题,把约束优化问题变成无约束优化问题,建立Lagrange函数:

式中,ai为拉格朗日乘子,对(4)式求偏导:∂L/∂w=0,∂L/∂b=0,∂L/∂ξ=0,∂L/∂a=0。

消去方程组中的ξi和w得到方程组:

式中,y=[y1y2… yN],L=[1 1 … 1],a=[a1a2… aN]T,Qi,j= φ(xi)Tφ(xj);i,j=1,2,…,N。
核函数 k(xi,xj)= φ(xi)Tφ(xj),k(xi,xj)是符合Mercer条件的核函数。这里采用径向基核函数(radial basis function,RBF)k(xi,x)=exp{- ‖x-xi‖2/δ2},解得上式b和a,故回归问题(1)式化为:

只需确定核函数的参量,简化了计算,提高了运算速度。常见的核函数有线性核函数k(xi,xj)=xixj,d 阶多项式核函数 k(xi,xj)=(xixj+1)d以及本文中采用的 RBF[14]。
2 实验
2.1 仪器和实验条件
实验中所用光源为波长为632.8nm的激光束(He-Ne激光器产生),成像设备为CCD相机(分辨率为1392像素 ×1040像素),使用 Simple-PCI软件(Hamamatsu公司开发)对图像进行分析和处理,获取图像的方法类似参考文献[15]。
2.2 试剂和样品
以脂肪乳注射液Intralipid(质量分数为0.20)作为散射介质(波长为632.8nm时,其散射系数μs=49.44mm-1,吸收系数 μa=0.117mm-1[16]),在可见光区,其光学特性参量与人体组织相当,且化学性质稳定。墨水作为吸收介质(天津鸵鸟牌中性墨水,632.8nm时吸收系数为 65.84mm-1[17]),稳定性好,无散射作用。使用Intralipid(质量分数为0.20)、墨水(0.75mL)和蒸馏水配制40组具有不同吸收系数(0.4cm-1~0.9cm-1)和散射系数(27cm-1~100cm-1)的组织模拟液,其中模拟液的有效散射系数μs′=5.4cm-1~20cm-1(各向异性因子g=0.8)。用CCD测量样品表面的漫反射光分布,获得40组实验样本,表1中列出其中15组样品的配制情况。

Table 1 Optical parameters of tissue-simulation phantoms
3 结果和分析
3.1 漫射光长度对预测精度的影响
样品1表面的漫反射光分布见图1;Simple-PCI软件对该图像进行分析和处理,获取漫反射相对光强随距离变化的情况如图2所示。从图2可以看出,在0mm~10mm范围内,样品表面的漫反射相对光强值不断减小;10mm以后,距离光束入射点较远的表面漫反射光很小且变化微弱,25mm处时减小为0。选取距离光入射点不同长度的漫射光数据,建立LS-SVM预测模型,分析漫射光数据长度对预测光学参量的影响。

Fig.1 Diffuse reflectance distribution on tissue simulation phantoms
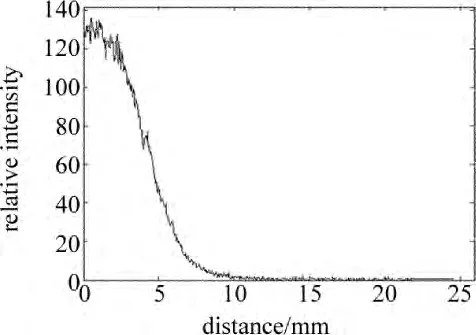
Fig.2 Diffuse relative intensity vs.distance
从40组样本中,随机选择30组作为训练集,其漫射光的数据长度分别选为15mm,20mm和25mm,将不同长度的漫射光数据输入到LS-SVM模型中,输出为光学参量,建立3种LS-SVM预测模型,对余下的10组样本进行预测。预测结果用10个测试样本的平均相对误差表示,计算公式为:ε100%,其中P(i)为预测值,T(i)为实验值。3种模型下,测试集中样本的吸收系数、有效散射系数的平均相对误差见图3。

Fig.3 Average predicted errors of different models
由图3可见,漫射光数据长度为15mm时,距离光入射点较近,所得数据未能完全反映样品表面的漫反射光分布,预测误差稍大;数据长度延长至20mm时,吸收系数和散射系数的平均预测误差均为5%,对光学参量的预测最准确。但是,过长的数据长度,如25mm,照射到样品表面的漫射光强明显降低,同时背景光和暗电流对其影响作用增强,造成较大误差。可见,利用漫反射光反演获得光学参量时存在最佳的漫射光数据长度,以下实验均选择漫射光数据长度20mm。
3.2 小样本下的预测情况
从40组样本中,随机选取10组(均匀抽样)作为测试集,从剩下的样本中分别选取样本数为30,15,7(均匀抽样)作为训练集1,2,3,建立LS-SVM 预测模型,对不同数量学习样本的LS-SVM预测能力进行测试和比较。
为获得一个LS-SVM模型(径向基核函数RBF)需要两个优化参量,上述提及的惩罚因子c及RBF内核函数的参量σ2,参量选择的好坏直接影响到模型的预测能力,本文中采用网格搜索法和10倍交叉验证法确定最优(c,σ)。将训练集输入到LS-SVM模型中,网格搜索各种可能的最优参量对(c,σ),然后进行交叉验证,直到找到使交叉验证精度最高的参量对,建立预测模型[18]。将不同数量的学习样本输入到LS-SVM模型中,通过寻优法找到最优参量,建立3种模型,对测试集中的样品进行预测,预测结果见图4。

Fig.4 Predicted results of three LS-SVM models
由图4直观地看出,建立的3种LS-SVM模型对10个未知样品的μs′和μa的预测值都十分接近真实值,即使训练样本数量为7情况,结果也较靠近真实值。3种模型对训练集中的样品也进行了预测,训练误差和预测误差见表2。

Table 2 Average predicted errors and training errors of three models
显然,训练集中的样品都得到精准的预测。对于测试集,训练集样本数为15时,LS-SVM模型对μs′和μa的平均预测误差均为6.2%,与学习样本为30的平均预测误差相比仅增加了1.2%,特别是在学习样本为7时,其预测精度高达93.6%。说明小样本情况下最小二乘支持向量机对光学参量有良好的预测效果。
为了进一步评估建立的小样本下的LS-SVM模型的性能,与人工神经网络(artificial neural network,ANN)和支持向量机两种方法进行比较。选择15个学习样本,分别建立3种方法的预测模型,对10个测试样品进行预测。平均预测误差及运行时间见表3。

Table 3 Predicted results of three methods
由表3可以看出,人工神经网络模型运算时间较短,但平均预测误差大;支持向量机模型的预测精度较神经网络模型有了明显提高,但耗时长;本文中采用的LS-SVM模型的预测结果最佳,用时仅为1s。可见,LS-SVM模型不仅提高了预测精度,而且加快了运算速度,充分表现了小样本条件下优越的预测性能。
4 结论
利用最小二乘支持向量机结合CCD测量技术对确定生物组织的光学参量进行了实验研究。结果表明:光学参量的预测存在最佳的漫射光数据长度;建立的小样本LS-SVM模型的预测效果较其它机器学习方法有了明显提高,对未知样本的μs′和μa的预测误差仅为5%,具有良好的预测性能。综上所述,利用最小二乘支持向量机结合CCD测量技术能够准确测量组织模拟液的光学参量,在实际测量生物组织的光学参量方面有广阔的应用前景。
[1] WAN Ch M.Analysis of the effective application range of diffusion approximation theory[J].Optical Technique,2002,28(2):137-138(in Chinese).
[2] ZHANG L,LI J.Experiment research for non-invasive measurement of optical parameters of biological tissues[J].Journal of North China Institute of Science and Technology,2008,5(2):75-77(in Chinese).
[3] WARNCKE D,LEWIS E,LOCHMANN S,et al.A neural network based approach for determination of optical scattering and absorption coefficients of biological tissue[J].Journal of Physics,2009,178(1):012047.
[4] ZHAO G H,LI Y,ZHAO J.Financial distress forecast of least squares support vector machines based on genetic algorithm parameter optimization[J].Science and Management,2011(5):56-61(in Chinese).
[5] VAPNIK V N.The nature of statistical leaning theory[M].New York,USA:Springer,1995:32-45.
[6] ZHU J Y,YANG Y,ZHANG H X.Data prediction with few observations based on optimized least squares support vector machines[J].Acta Aeronautica et Astronautica Sinica,2004,25(6):566-568(in Chinese).
[7] YAN W W,SHAO H H.Application of support vector machines and least squares support vector machines to heart disease diagnoses[J].Control and Decision,2003,18(3):359-360(in Chinese).
[8] LI L J.The study of modeling algorithm based on LS-SVM and predictive control algorithm[D].Hangzhou:Zhejiang University,2008:1-109(in Chinese).
[9] YANG Y R,YANG R J,ZHANG Zh Y.Discrimination of adulterated milk using least square support vector machines combined with two-dimensional correlation infrared spectroscopy[J].Acta Photonica Sinica,2013,42(9):1124-1127(in Chinese).
[10] KIENLE A,LILGE L,PATTERSON M S,et al.Spatially resolved absolute diffusereflectance measurements for noninvasive determination of the opticalscattering and absorption coefficients of biological tissue[J].Applied Optics,1996,35(13):2304-2314.
[11] JIANG A N,LIANG B.Nonlinear time series prediction model for dam seepage flow based on PSO_SVM[J].Journal of Hydraulic Engineering,2006,37(3):331-335(in Chinese).
[12] YAN W W,ZHU H D,SHAO H H.Soft sensor modeling based on support vector machines[J].Journal of System Simulation,2003,15(10):1494-1496(in Chinese).
[13] GU Y P,ZHAO W J,WU Zh S.Least squares support vector machine algorithm[J].Journal of Tsinghua University(Science and Technology Edition),2010,50(7):1064-1071(in Chinese).
[14] ZHOU Y R,TENG Zh Sh,ZHAO X W.Fast online system identification for MIMO using LSSVM[J].Journal of Computer Applications,2009,29(8):2282-2314(in Chinese).
[15] YANG L,SHUN J H,ZHANG L Sh.Experimental research for noninvasive measurement of optical parameters of biological tissues by using CCD[J].Journal of Civil Aviation University of China,2010,28(3):42-44(in Chinese).
[16] di MINNI P,MARTELLI F,ZACCANTI G.Effect of dependent scattering on the optical properties of Intralipid tissue phantoms[J].Biomedical Optics Express,2011,2(8):2265-2278.
[17] ZHANG L Sh,WANG Zh Zh,ZHOU M Y.Determination of the optical coefficients of biological tissue by neural network[J].Journal of Modern Optics,2010,57(13):1164-1170.
[18] WANG K Q,YANG Sh Ch,DAI T H.Method of optimizing parameter of least squares supportvector machines by genetic algorithm[J].Computer Applications and Software,2009,26(7):110-111(in Chinese).

