一种视觉引导经纬仪自动测量中精确引导方法

吴 斌，苏晓越

(天津大学精密测试技术及仪器国家重点实验室，天津300072)

引 言

随着大型装备制造技术的提高，在大空间对大尺寸工件特征点、长度及曲面特征等的精密测量已成为工业测量领域的研究热点和难点。利用激光跟踪仪、全站仪、经纬仪和摄影测量相关设备是实现大空间、大尺寸物体精密制造、装配的主要测量手段［1-4］。随着电子技术、信息处理技术的进步以及测量理论的发展，针对大尺寸空间测量应用，又发展了以美国GSI公司的V-STARS为代表的工业摄影测量系统以及以Nikon公司的iGPS为代表的室内空间定位测量系统［5］。电子经纬仪具有较广的测量范围和较高的测量精度，测量空间特征点的3维坐标时，通过粘贴标记点而不需要合作靶标，但由于测量时需要依靠人眼瞄准，导致测量效率较低，无法实现自动化测量［6］。ZHANG等人对激光电子经纬仪自动测量系统作了相关研究，其利用Leica TM5100A型电子经纬仪，在传统经纬仪前方交会测量原理的基础上，通过增加由2维精密转台及高分辨率摄像机组成的视觉跟踪测量子系统，利用相机自动跟踪瞄准代替人眼瞄准，减少了人眼瞄准的误差，同时利用由工件理论设计数模文件为指导，结合特征图像的自动识别和匹配提高了系统的测量效率［7］。该方法在大尺寸空间中大型装备，如飞机、轮船、高速列车等几何形貌的特征测量及大型建筑，如大桥、水坝的变形监测方面具有极其重要的意义。

1 系统工作原理

视觉跟踪引导激光经纬仪自动测量系统模型如图1所示，该系统由两部分组成，一是激光经纬仪测量子系统，另一部分是视觉跟踪引导测量子系统。该系统测量过程总体可分为4步:(1)双经纬仪精确定向并标定激光经纬仪测量子系统与视觉跟踪子系统;(2)由工件理论设计数模文件，引导两测量子系统瞄准被测特征点所在区域并聚焦使图像清晰;(3)精确引导两子系统，使双经纬仪激光点交会于特征点;(4)重复第(2)步～第(3)步，完成全部特征点测量并计算出3维坐标。测量过程中，精确引导方法直接决定了测量系统最终的准确度和效率。ZHANG等人采用的精确引导方法利用摄像机视场中激光光斑中心与特征点中心的像素关系构建图像像素距离与测量空间关系模型，从而实现对经纬仪的精确引导［7］。由于存在近似关系，在精确引导过程中需要多次判别图像中经纬仪发出的激光光斑中心与目标点中心位置关系，并使两台经纬仪相应作小角度转动最终精确瞄准目标点，此方法尽管可以获得较高的测量准确度，但由于经纬仪自身结构限制，多次移动使得测量花费时间较长，测量效率却很低。本文中提出一种基于摄像机光轴的精确引导方法，初始引导完成后，该方法首先使摄像机光轴对准空间目标点，再利用摄像机光轴与双经纬仪的关系，可使双经纬通过一次移动交会在目标点，在保证测量准确度的同时缩短测量的时间，提高测量效率。

Fig.1 Schematic diagram of the measurement system

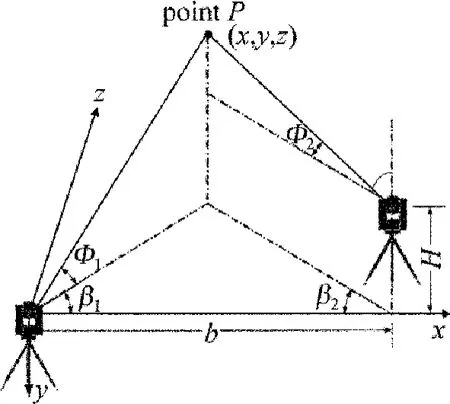
Fig.2 Mathematical model of double-theodolite measuring system

视觉跟踪引导激光经纬仪自动测量系统由两台Leica公司的TM5100A型电子经纬仪构成，该型经纬仪带有伺服驱动功能，其上的DL2激光指示器与经纬仪视准轴同轴，在对被测目标进行标识的同时，兼具经纬仪测量瞄准方向的空间可视化。图2所示为双经纬仪测量系统空间前方交会测量数学模型，以左经纬的中心为坐标原点，从两经纬仪中心线在水平方向上的投影作为x轴，方向为从左经纬仪指向右经纬仪;通过左经纬仪中心方向向下的铅垂轴作为y轴;最后根据右手法则得到z轴方向，精确定向后建立如图所示的坐标系作为世界坐标系。图2中b为双经纬仪中心水平距离，H为双经纬仪中心高度差，Φ1和Φ2分别为左右经纬仪瞄准空间点P时的垂直角，β1和β2分别为左右经纬仪瞄准空间点P时的水平角，根据空间前方交会原理完成双经纬仪测量系统的测量功能［8］。视觉跟踪子系统由一台2维精密转台和一台具有30倍光学伺服变焦的CCD相机构成，相机固定在精密转台上，随精密转台水平或垂直转动，可以实现对空间目标点及经纬仪激光点的识别。初始对空间目标点和激光特征标识搜索跟踪时，采用短焦距、大视场、低分辨率的成像模式，实现区域跟踪;进而增大焦距、缩小视场、提高图像分辨率，为精确引导两经纬仪激光点交会于空间目标点提供保障。

2 视觉跟踪引导数学模型

2．1 基于数模引导的初始引导方法

数模文件是指工件的理论设计数据经过坐标转换后导入经纬仪坐标系下的坐标数据文件。数模文件对经纬仪的引导可由被测工件与经纬仪测量系统的位置关系来实现，而数模文件对跟踪相机的引导及由相机跟踪结果对经纬仪系统的引导，还需要在上述关系的基础上，预先对经纬仪测量系统与视觉跟踪系统的关系进行标定，也是解决系统测量问题的关键。当精密转台作水平或垂直旋转时，固定于转台末端上的摄像机随之作相应转动。因此，欲建立摄像机坐标系与经纬仪坐标系之间的关系可以通过以下3步得到:(1)建立精密转台初始位置坐标系与经纬仪坐标系的关系;(2)精密转台末端平台实时位置坐标系的确立;(3)建立摄像机坐标系与末端平台实时位置坐标系的关系。图3所示为坐标转换示意图，假设世界坐标系为(xw，yw，zw)，转台初始坐标系为(xy，0，yy，0，zy，0)，末端平台实时位置坐标系为(xy，m，yy，m，zy，m)，摄像机坐标系为(xc，yc，zc)。

Fig.3 Mathematical model of vision tracking measurement system and relationship map of coordinate transformation

2.1.1 建立世界坐标系与精密转台坐标系的关系双经纬精确定向后，将一ZrO2陶瓷球(G10级，GB308-2002/ISO3290-1998)固定在转台末端平台上，分别让转台水平、垂直旋转几个角度，并测出陶瓷球在各个位置处在经纬仪坐标系下的圆心坐标值。精密转台水平旋转时，陶瓷球移动轨迹是一段圆弧，由各陶瓷球圆心坐标拟合该圆弧并求得圆弧圆心坐标及圆弧所在平面的法矢量，该法矢量即为精密转台垂直旋转轴z轴。同理，可以求得转台水平旋转轴x轴，最后由右手法则确定出y轴。

2.1.2 2维精密转台末端平台实时坐标系的确定设转台末端平台实时坐标系为(xy，m，yy，m，zy，m)，转台绕水平方向旋转轴旋转角度α、往垂直方向旋转轴旋转角度θ，则可以得到转台初始坐标系与末端平台实时坐标系的关系:

式中，

设一空间点X在世界坐标系下坐标为(xw，yw，zw)，在转台初始位置坐标系下坐标为(xy，0，yy，0，zy，0)，则有:

式中，M1=为 x 轴方向矢量，(iy，jy，ky)为 y 轴的方向矢量，(x0，y0，z0)为初始垂直轴与水平轴间方位参量。M1由第(1)步标定得到。

由(1)式、(3)式，可以求得世界坐标系和转台实时坐标系的关系:

2.1.3 摄像机坐标系与末端平台实时坐标系的关系

摄像机坐标系与转台末端平台位置实时坐标系的关系需要借助经纬仪坐标系作为中介来标定。将如图4所示的平面靶标置于测量区域，该靶标行列间距均为30mm，且左右两边列的圆心中有“+”特征。首先，根据ZHANG标定算法［9］解算摄像机内外参量，得到摄像机与平面靶标坐标系的关系。然后瞄准靶标上4个角上靶心，利用基于多公共点坐标转换法［10］求得平面靶标坐标系与经纬仪坐标系之间的关系，再根据上述两节中所述转台末端平台实时位置坐标系和经纬仪坐标系的关系，进而实现末端平台实时位置坐标系和摄像机坐标系的关系标定。

Fig.4 Planar target

设靶标上任意一个特征标记中心在靶标坐标系下的坐标为(x，y，0)，在摄像机坐标系下的坐标为(xc，yc，zc)，在经纬仪世界坐标系下的坐标为(xw，yw，zw)，当前摄像机坐标系与靶标坐标系间的转换矩阵为M2，则有:

式中，M2=

设经纬仪坐标系与靶标坐标系的转换矩阵为Mr，则有:

联立(5)式、(6)式，可得当前摄像机坐标系到经纬仪世界坐标系的转换关系为:

由(4)式、(7)式可得转台末端平台实时坐标系与摄像机坐标系的关系:

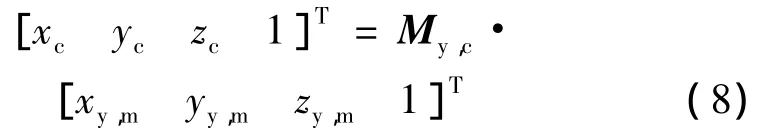
式中，My，c=M2·Mr·M1·Mrotate。由于摄像机固定于末端平台，因此My，c也可预先标定。

于是，联立(4)式、(8)式可得经纬仪坐标系与实时摄像机坐标系的关系，即视觉跟踪引导数学模型:

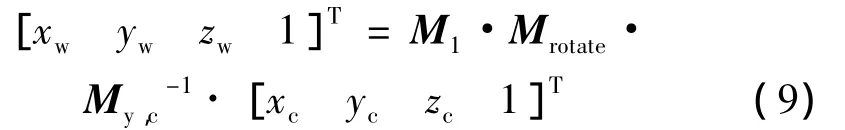
测量时，被测特征若成像于跟踪相机的像面中心处，即跟踪相机的光轴过被测特征，则由(9)式及精密转台的水平和垂直转台转过的角度，可得经纬仪指向被测特征时应转过的水平角及垂直角。

2．2 基于摄像机光轴引导的精确引导策略

由于工件的理论设计数据往往与生产加工后特征点的实际坐标值有比较大出入，因此对测量系统进行数模引导后，工件的特征中心点往往不会位于摄像机的视场中心。本文中提出采用摄像机光轴对双经纬仪进行精确引导的方法，即标定双经纬仪测量子系统与视觉跟踪引导子系统，用数模文件对系统进行初始引导后是图像清晰成像于视场中，利用数字图像处理技术配合精密转台转动使得特征点成像于相机视场中心，最后根据两子系统之间的关系使得双经纬仪通过一次移动精确瞄准待测特征点中心，图5为精确引导前后测量系统示意图，具体测量方法如下:(1)保存数模引导后摄像机视场中的图像;(2)利用椭圆拟合的方法［11］结合OpenCV视觉库中图像处理函数提取图像中特征点中心的像素坐标(xt，yt)，并与图像中心点像素坐标(x0，y0)做比较得出水平和垂直差值px，py;(3)驱动云台在水平与垂直方向各移动1步(1步即为云台可移动的最小角度0.0125°)，重复第(2)步，计算出云台微动1步后两中心点水平与垂直像素上的变化值Δpx，Δpy;(4)计算出云台在x方向上需要移动的步数px/Δpx和y方向上的需要移动的步数py/Δpy，并驱动云台移动相应步数;重复第(2)步、第(3)步、第(4)步直到px与py在1个像素以内;(5)将精密转台转过的总的水平角与垂直角按第2.1节中所述方法转换为双经纬仪需要转过的水平角和俯仰角，并驱动激光经纬仪转动相应角度值;(6)读出当前经纬水平角和垂直角并计算出该点3维坐标。重复上述第(1)步～第(5)步直到所有特征点测量完成。

Fig.5 Schematic diagram of the measurement system before and after precise guiding

3 系统构建与实验验证

实验搭建的激光经纬仪测量系统由两台Leica公司的TM5100A型电子经纬仪构成，视觉跟踪系统由日本东芝公司的CS8620Ci摄像机和TOKINA公司的TM33Z1540NPN电动变焦镜头组成。

如图6所示搭建测量系统，并在系统前方任意放置几个标记点。利用精确互瞄法建立双经纬仪坐标系。利用人眼瞄准测量其精度可以达到微米到10μm量级，因此人眼瞄准测量结果可以作为测量基准［8］，故将系统自动引导测量的结果与其比对。实际测量时，对每个测点采用多次测量取平均值作为测量结果以消除人眼瞄准误差的影响。

Fig.6 Experiment system

首先，对每个被测点进行3次人眼瞄准测量并求取平均值作为测量基准值。其次，依次测量空间特征点并求解其3维坐标值，将自动引导测量结果与人眼瞄准测量结果进行比对，并分别计算所有特征点在3个方向上的偏差值，表1所示为自动测量数据与人眼瞄准测量值之间的误差值表，图7所示为自动测量值与人眼瞄准测量值的误差曲线图。

Table 1 Measurement results and errors of the automatic measurement system

Fig.7 Errors curves between automatic measurement and manual measurement

实验数据及误差图表显示:利用基于摄像机光轴的精确引导方法，自动引导测量得到各个特征点在3个方向上的偏差值均在±0.3 mm以内，满足大尺寸坐标测量的要求。

4 结论

在传统经纬仪前方交会测量原理的基础上，利用新型电子经纬仪的同视准轴准直激光指示特性，结合视觉测量跟踪技术，研究了一种基于摄像机光轴对电子激光经纬仪的精确引导方法。该方法无需合作靶标，在保证较高精度的同时提高了测量效率，实现了大尺寸空间大型工件的自动、快速、高精度测量。对于大尺寸空间、大型工件(装备)，如船舶、大型飞机、航天器、高速列车等的几何形貌特征测量，以及大型建筑、水坝等的变形监测等具有十分重要的意义。

［1］ PEGGS G N，MAROPOULOS P G，HUGHES E B，et al.Recent developments in large-scale dimensional metrology［J］.Proceedings of the Institution of Mechanical Engineers，2009，B223(6):571-595.

［2］ CUYPERS W，van GESTEL N，VOET A，et al.Optical measurement techniques for mobile and large-scale dimensional metrology［J］.Optics and Lasers in Engineering，2009，47(3):292-300.

［3］ MAUTZ R.Overview of current indoor positioning systems［J］.Geodesy and Cartography，2009，35(1):18-22.

［4］ HOPE C，MARCELO C.Manual total station monitoring［J］.Geotechnical News，2008，26(3):28-30.

［5］ WANG Z，MASTROGIACOMO L，FRANCESCHINI F，et al．Experimental comparison of dynamic tracking performance of iGPS and laser tracker［J］.The International Journal of Advanced Manufacturing Technology，2011，56(1/4):205-213.

［6］ ZHOU F Q，ZHANG G J，JIANG J.Three-dimensional coordinate measuring system with bino-theodolites on site.［J］.Chinese Journal of Mechanical Engineering，2004，40(1):165-169(in Chinese).

［7］ ZHANG Z L.Study on the large-scale space coordinate measurement method based on vision guidance［D］.Tianjin:Tianjin University，2010:42-46(in Chinese).

［8］ LONG W H，ZHAI C.The principle of spatial forword intersection and discussion about Its applications［J］.Metrology＆ Measurement Technology，2006，25(6):51-54(in Chinese).

［9］ ZHANG Zh Y.A flexible new technique for camera calibration［J］.IEEE Xplore，2000，22(11):1330-1334.

［10］ FU J，CHU W，DIXSON R，et al.Three-dimensional image correction of tilted samples through coordinate transformation［J］.Scanning，2008，30(1):41-46.

［11］ YAN B，WANG B，LI Y.Optimal ellipse fitting method based on least——square principle ［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(3):295-298(in Chinese).