基于循环谱和高阶累积量的联合模式识别方法*

陈泽艺

(重庆邮电大学 通信学院，重庆400065)

1 引 言

通信信号调制模式识别是在多信号环境和噪声条件下确定信号的调制模式，是信号监测和进一步解调分析的基础和前提。在非协作通信、电子对抗、信号干扰与截获等军民领域都具有重要应用。常用的信号调制模式识别方法主要基于决策理论、神经网络和统计理论。基于决策理论的调制识别方法所用参数需要搜索最优门限，参数提取和信号识别的顺序对识别率影响极大，参数及特征选取复杂;神经网络识别结构复杂，计算量大，硬件复杂高;基于统计理论的调制模式识别方法具有良好的识别性能，因而获得了广泛应用。

以信号的高阶累积量作为特征参数进行调制识别，抗噪性能好，计算复杂度低［1］，二进制幅移键控(2ASK)和二进制相移键控(Binary Phase Shift Keying，BPSK)的高阶累积量以及MFSK 的高阶累积量相等，不足以区分信号，高阶累积量识别法无法完全区分卫星通信中主要调制方式［2－4］。闫朋展等［3］应用二叉树支持向量机(Support Vector Machine，SVM)与高阶累积量相结合识别ASK、PSK、QAM 信号，在低信噪比下具有很好的识别率，但识别实验中没有加入FSK 信号。针对FSK 类信号高阶累积量完全相同无法识别的情况，李彦栓等［5］人对FSK 信号先进行一阶微分后再求取高阶累积量，完成了2ASK、4ASK、QPSK、2FSK、4FSK 信号的分类。党月芳等［6］应用分形理论对高阶累积量法进行了补充，能够完成主要调制方式的分析。循环谱识别方法在低信噪比时具有较高的识别率［7－8］，但在实现2FSK与4FSK 信号分类时需要利用谱峰个数及谱幅度等，难度较大;在实现BPSK、QPSK 信号分类时，由于两者功率谱密度函数十分相似，识别困难。文献［9］提出用循环谱密度函数三维图像截面图的不同实现了两者的区分，但计算量过大，不易硬件实现。

本文采用循环谱和高阶累积量识别法，通过多种特征参数联合判决构建简单的级联结构实现了一种联合识别算法。该算法运用循环谱对ASK、MFSK、PSK 信号进行预分类处理，弥补高阶累积量识别缺陷，在利用循环谱对信号进行分类的基础上，利用高阶累积量完成ASK、PSK 信号的类内区分，提高了识别率。仿真分析表明，该算法对现有主要调制方式具有很高的识别率。

2 调制模式识别特征定义

信号的特征参数选取是调制识别的关键，直接决定了识别性能。信号的高阶累积量特征具有抗噪性，但对于2FSK、4FSK 等具有相同的累积量，而循环谱对于不同种类信号有较好的区分性。根据联合算法的设计特点，在循环谱特征识别中选择了调制类别区分度较高的包络特性，在高阶累积量特征选择中采用对同类调制模式区分度较高的参数。

2.1 循环谱特征理论

信号x(t)为一广义循环平稳随机过程，其自相关函数定义为

式中，T 为信号码元周期，τ 为延迟时间，则信号x ( t)的循环自相关函数定义为

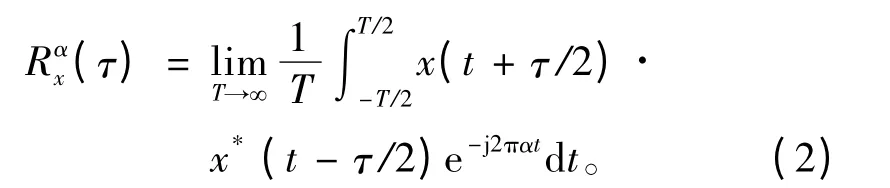
使Rαx(τ)≠0 的频率α 称为信号的循环频率，α=k/T，k 为整数。一个循环平稳信号的循环频率可能有多个，其中包括零频率和非零频率。当α =0时，R0x()τ 为平稳信号的自相关函数;当α≠0 时，Rαx()τ 为Rx()τ 的周期加权形式，称为周期自相关函数，也即循环自相关函数［2］。循环自相关函数Rαx()τ 的傅里叶变换Sαx()f 为信号 ()x t 的循环谱:

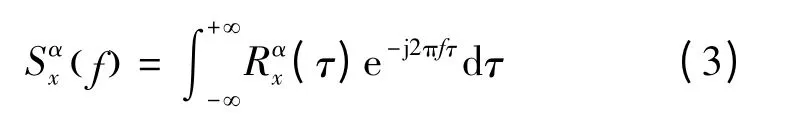
ASK 信号、PSK、FSK 信号包络特性差异较大，根据各类信号的特点选取3 个特征值M1、M2、M3。特征值M1=1/σS0，其中σS0为信号 ()x t 归一化循环谱Sαx()0 截面幅度包络方差;特征值M2=1/σSfc，其中为信号 ()x t 归一化循环谱截面幅度包络方差;特征值M3=1/u，u 为信号归一化循环谱Sαx()0 截面幅度包络均值。

2.2 高阶累积量特征理论

对于平稳随机过程 ()x t ，其p 阶混合矩为［3］

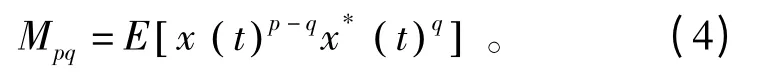
则其二阶、四阶、六阶累积量分别为

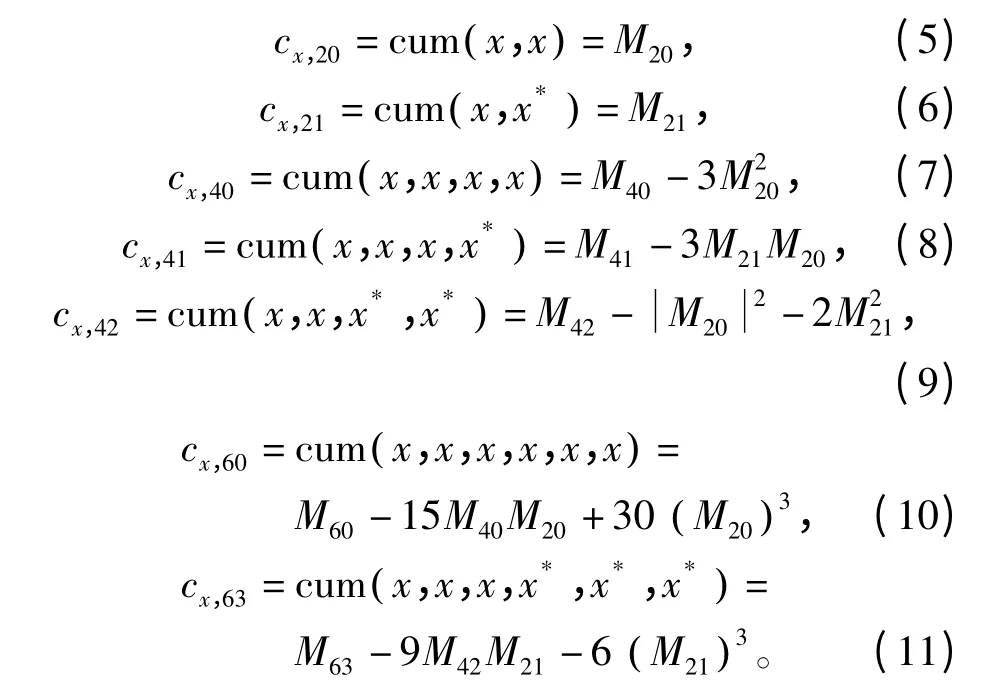
通过式(4)～(11)可计算出不同调制信号高阶累积量如表1所示，本文选择四阶和六阶高阶累积量，构造特征参数构造参数区分2ASK 和4ASK 信号，选择四阶高阶累积量构造特征参数可以区分BPSK 信号和QPSK 信号。

表1 不同数字调制信号的高阶累积量Table 1 High－order cumulants of different digital modulation signals

3 联合识别算法设计

循环谱特征参数对于不同类别的调制模式较为敏感，识别精度高。联合识别算法原理如图1所示，第一步由循环谱特征识别对调制方式分类，可以识别ASK、PSK、2FSK、4FSK 调制信号;第二步采用高阶累积量特征识别，联合循环谱特征进一步识别2ASK、4ASK、BPSK、QPSK。两级识别间靠特征值传递，计算复杂度低。由表1可知，除FSK 以外同一调制类别的高阶累积量差异较大，区分精度更高。

图1 联合识别算法原理图Fig.1 Principle of combined modulation recognition algorithm

将循环谱与高阶累积量两种识别特征相结合，能够完全区分主要的调制方式，算法工作流程见图2，详细算法描述如下:

(1)对接收的数字调制信号进行下变频处理后得到基带调制信号;

(2)计算信号 x ( t)的归一化循环谱，并提取Sαx( 0)截面的幅度包络方差σS0，构造参数M1=1/σS0并与门限值t1比较，将信号分为{2ASK、4ASK}、{2FSK、4FSK、BPSK、QPSK}两类，其中M1＞t1时为ASK 类信号，反之为FSK 和PSK 类信号;

(3)在步骤2 识别基础上，提取信号 x ( t)归一化循环谱Sαx( fc)截面的幅度包络方差σSfc，构造参数M2=1/σSfc并与门限值t2比较，将信号分为FSK 和PSK 两类，其中M2＞t2时为PSK 类信号，反之为FSK 类信号;

(4)若 ()x t 为FSK 类信号，则跳至步骤5;若为ASK 类信号，则跳至步骤6;若为FSK 类信号，则跳至步骤7;

(5)计算信号 ()x t 的归一化循环谱Sαx()0 截面幅度包络均值u，构造参数M3=1/u 并与门限值t3比较，完成2FSK、4FSK 信号的识别;

(6)计算信号 x ( t)的四阶累积量C40、六阶累积量C60，构造参数并与门限值t4比较，完成2ASK、4ASK 信号的识别;

(7)计算信号 x ( t)的四阶累积量C41、C42，构造参数并与门限值t5比较，完成BPSK、QPSK 信号的识别。

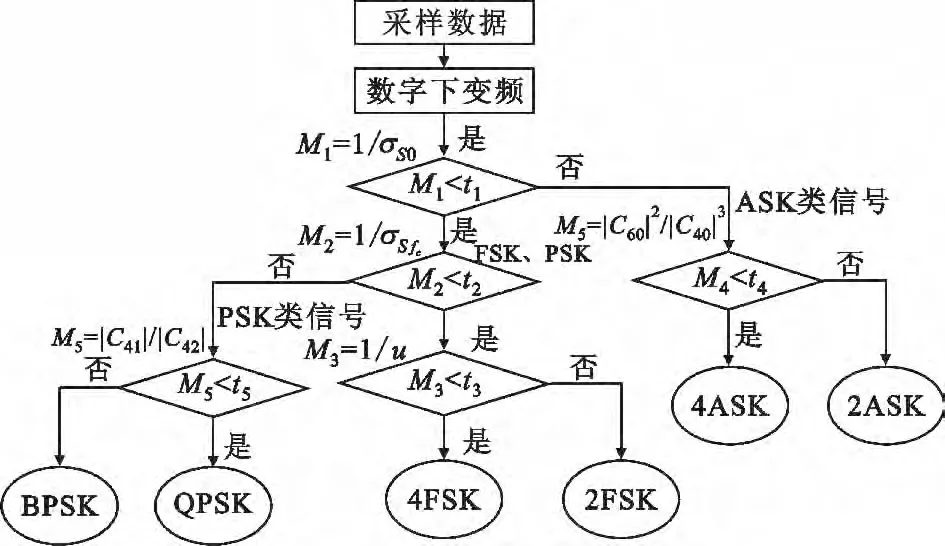
图2 联合识别算法流程图Fig.2 Flow chart of combined modulation recognition algorithm

4 仿真与结果分析

基于MATLAB 环境，采用联合算法对{2ASK、4ASK、2FSK、4FSK、BPSK、QPSK}6 种信号进行识别仿真，考虑到参数指标过高会引起采样率高、仿真时间加长以及需要复杂的多速率转换，且数据率、载波品类的等参数与识别率无关等，仿真参数设定为:信号载波频率fc=150 kHz，采样频率fs=1200 kHz，码元速率Rb=25 kHz，加性高斯白噪声环境，进行100次独立Monte Carlo 仿真实验，图3～7给出了在不同信噪比条件下各种信号调制模式下的特征参数变化曲线。

ASK 信号与FSK、PSK 类信号调制类别识别如图3所示，由图可知ASK 类信号的M1参数明显高于其他类信号，因此将信号 ()x t 的M1参数与设定阈值t1比较即可将ASK 类信号(M1＞t1)与{FSK、PSK}(M1＜t1)类信号区分开来。

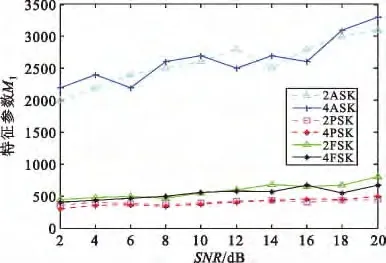
图3 ASK 与FSK、PSK 调制识别Fig.3 Recognition of ASK and FSK，PSK

FSK 与PSK 类信号识别如图4所示，由图可知PSK 类信号M2参数明显大于FSK 类信号，因此将信号 ()x t 的M2参数与设定阈值t2比较即可准确地将PSK 类信号(M2＞t2)与FSK 类信号(M2＜t2)区分开来。

图4 PSK 与FSK 调制识别Fig.4 Recognition of PSK and FSK

2FSK 和4FSK 信号识别如图5所示，由图可知2FSK 信号M3参数值明显大于4FSK 信号，因此将信号 ()x t 的M3参数与设定阈值t3比较即可将2FSK(M3＞t3)与4FSK(M3＜t3)信号区分开来，从而实现FSK 信号的类内识别。

图5 2FSK 与4FSK 调制识别Fig.5 Recognition of 2FSK and 4FSK

通过构造参数M1、M2、M3能够实现FSK、ASK 、PSK 类信号的类间识别及FSK 信号的类内识别，但无法实现ASK、PSK 信号的类内识别，而参数M4和M5可以完成类内识别。

ASK 类信号识别M4参数曲线如图6所示，由图可知通过2ASK 信号M4参数值明显大于4ASK信号，因此通过计算信号 ()x t 的高阶累积量及M4参数，并与设定阈值t4比较即可将2ASK(M4＞t4)与4ASK(M4＜t4)信号区分开来，从而实现ASK 信号的类内识别。

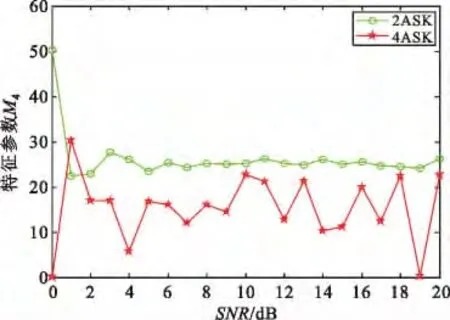
图6 2ASK 与4ASK 调制识别Fig.6 Recognition of 2ASK and 4ASK

PSK 类信号识别如图7所示，BPSK 信号M5约等于1，而QPSK 信号的M5参数值趋近于0，因此通过计算信号 ()x t 的高阶累积量及M5参数，并与设定阈值t5比较即可将BPSK(M5＞t5)与QPSK(M5＜t5)信号区分开来，从而实现PSK 信号的类内识别。

图7 BPSK 与QPSK 调制识别Fig.7 Recognition of BPSK and QPSK

综上所述，通过联合多种判决特征参数，能够解决ASK、FSK、PSK 类信号的通用识别问题，联合识别算法的识别结果见表2，在信噪比(Signal－to－noise Ratio，SNR)大于等于5 dB 时识别率已达到88%以上，10 dB时总体识别率达到93%，15 dB时识别率超过了95%，与文献［4－5，7］相比识别率有显著提高，与改进的高阶累积量识别法［6］相比，性能仍有所提高。该方法解决了ASK、FSK、PSK 类信号通用识别问题，在卫星通信信号识别领域，对于盲侦测接收机、自适应通信系统的数字调制方式识别技术的工程实现具有较好的参考价值。

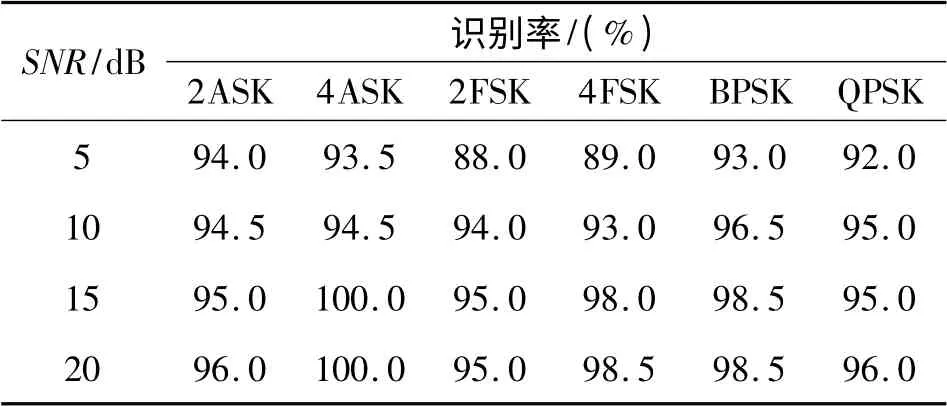
表2 联合识别算法识别结果Table 2 Simulation results of combined modulation recognition algorithm

5 结束语

高阶累积量识别法具有良好的抗干扰识别性能，但无法完全识别主要的调制方式，限制了其应用范围和实用性。本文针对卫星通信中对ASK、FSK、PSK 类调制模式识别需求，将循环谱特征引入高阶累积量构建新的级联识别器，扩展高阶累积量的识别范围，提高了识别效率和精度。该识别算法能够完全识别{2ASK、4ASK、2FSK、4FSK、BPSK、QPSK}，覆盖了常用的卫星通信调制方式，具有很好的工程实用价值。由于计算循环谱特征参数和高阶累积量仍然需要较大的数学运算量，在工程应用可采用专有硬件实现。此外，该方法中没有引入智能决策算法(如神经网络、支撑向量机)，在一定程度上影响了识别率，这将是下一步的研究内容。

［1］ 王永娟. 基于高阶累积量的OFDM 信号调制识别技术研究［D］. 西安:西安交通大学，2009.WANG Yongjuan. Research on Modulation Identification of OFDM Based on High Order Cummulants［D］. Xi'an:Xi'an Jiaotong University，2009.(in Chinese)

［2］ WANG Lanxun，REN Yujing，ZHANG Ruihua. Algorithm of digital modulation recognition based on support Vector machines［C］∥Proceedings of 2009 International Conference on Machine Learning and Cybernetics. Baoding:IEEE，2009:980－983.

［3］ 闰朋展，王振宇.运用高阶累积量和SVM 的调制自动识别［J］.电讯技术，2010，50(10):36－40.YAN Pengzhan，WANG zhenyu. Automatic recognition of digital modulation signals applying high order cumulants and support vector machines［J］. Telecommunication Engineering，2010，50(10):36－40.(in Chinese)

［4］ 谭晓衡，刘娟，胡友强.一种新的低信噪比下的效字调制识别方法［J］. 系统工程与电子技术，2009，31(6):60－64.TAN Xiaoheng，LIU Juan，HU Youqiang. A new algorithm for digital modulation recognition under the low SNR［J］.Systems Engineering and Electronics，2009，3l(6):60－64.(in Chinese)

［5］ 李彦栓，罗明，李霞. 基于高阶累积量的OFDM 信号调制识别技术［J］.电子信息对抗技术，2012，27(4):1－4.LI Yanshuan，LUO Ming，LI Xia. Modulation Identification of OFDM Based on High Order Cummulants［J］. Electronic Information Warfare Technology，2012，27(4):1－4.(in Chinese)

［6］ 党月芳，徐启建，张杰，等. 高阶累积量和分形理论在信号调制识别中的应用研究［J］. 信号处理，2013，29(6):762－765.DANG Yuefang，XU Qijian，ZHANG Jie，et al. Research Modulation Classification Based on Higher－Oder Cumulants and Fractal Theory［J］. Journal of Signal Processing，2013，29(6):762－765.(in Chinese)

［7］ 饶伟. 多径衰落环境中具有调制识别能力的盲均衡新算法［J］. 电子学报，2013，41(7):1284－1289.RAO Wei. New Blind Equalization Algorithm with Ability of Modulation Classification Under the Condition of Multipath Propagation［J］. Acta Electronica Sinica，2013，41(7):1284－1289.(in Chinese)

［8］ 余志斌，于宁宇. 基于循环谱包络的多信号调制识别［J］. 计算机应用，2012，32(8):2119－2122.YU Zhibin，YU Ningyu. Modulation recognition or multi－component PSK signals based on cyclic spectrum amplitude［J］. Journal of Computer Applications，2012，32(8):2119－2122.(in Chinese)

［9］ 郑天堃. 非协作通信接收机中调制信号识别技术研究［D］. 绵阳:西南科技大学，2014.ZHENG Tiankun. Research on modulation recognition technology of uncooperative communication receiver［D］.Mianyang:Southwest University of Science and Technology，2014.(in Chinese)