一种联合星座和伴随式信息的迭代译码算法*
陈海强,王 璐,黄小栗,罗灵山,梁 奇,覃团发,2,3
(1.广西大学 计算机与电子信息学院,南宁530004;2.广西高校多媒体通信与信息处理重点实验室(广西大学),南宁530004;3. 广西多媒体通信与网络技术重点实验室培育基地(广西大学),南宁530004)
1 引 言
伴随式信息属于二元域信号,能够方便地从接收端的硬判决信息中提取,广泛用于各类前向纠错码(Forward Error Correction,FEC)技术中。传统的基于硬判决的低密度奇偶校验(Low Density Parity Check,LDPC)译码算法,例如比特翻转算法(Bit Flipping,BF)[1]和一步大数逻辑译码(One Step Majority Logic Decoding,OSMLGD)算法[2]等都使用了伴随式信息进行译码设计。在硬判决译码的基础上引入可靠度信息以及迭代译码,衍生了近年来颇受关注的基于可靠度的译码算法,这类算法能有效兼顾译码复杂度、收敛和译码性能。
典型的基于可靠度的译码算法包括加权一步大数逻辑(Weighted OSMLGD,WOSMLGD)译码[2]、加权比特翻转算法以及它们的改进版本等[3]。基于可靠度信息,引入适当的迭代策略可以进一步提高译码性能。相关的工作包括近年来由Huang 等人提出的基于可靠度的迭代大数逻辑译码算法(RBI-MLGD)[4]以及基于该算法的各种改进算法,如WISRB-MLGD 算法[5]、MRBI-MLGD 算法[6]以及Ngatched[7]和Zhang[8]等人提出的修正算法等。基于可靠度的多元LDPC 译码算法近年来也得到了研究[9]。
上述几种基于可靠度的译码算法都使用了一种特殊的外信息形式,需要结合当前码位信息和伴随信息进行提取。这个过程会产生额外的运算操作,对于码长较长、列重较大的大数逻辑可译码,会产生不可忽视的运算开销。此外,变量点的总外信息设计(偏移幅度/方向)是跟信源端的星座映射相关的,而上述几种算法都没有引入星座信息。基于此,本文联合信号星座和伴随式信息进行译码设计。在校验节点,我们直接使用伴随式信息进行传递和处理;在变量节点,结合信源端的星座映射和伴随式进行总信息收集和处理。由于伴随式信息是二元信息,因此本文的算法也属于二元信息传递算法。理论分析和仿真实验结果表明,本文提出的算法在保持原RBI-MLGD 算法优良译码性能的同时,具有更低的译码复杂度。
2 系统模型
信息序列u =(u0,u1,…,uk-1)∈Fk2经编码后得到码字c=(c0,c1,…,cn-1)∈Fn2。c 经调制后得到实数向量x =(x0,x1,…,xn-1),其中xj=φS(cj)∈R是一个维的实数信号,其形式由具体的映射规则φS(·)决定,相应的信号星座记为As{φS(cj),cj∈F2}。对于二元域信号,可采用简单的一维BPSK 映射。本文提出的算法将结合具体的 φS(·)函数对变量点译码策略进行描述。假设信号x通过加性高斯白噪声信道(Additive White Gaussian Noise Channel,AWGNC)传输,接收信号为y =(y0,y1,y2,…,yn-1),yj=xj+nj,其中,ni~N(0,σ2)是高斯白噪声的一个实现。接收信号y 经量化处理得到q=(q0,q1,…,qn-1)。
3 RBI-MLGD 译码算法回顾
计算硬判决信息z=(z0,z1,…,zn-1),其判决规则为
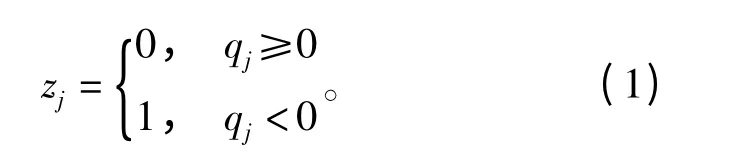
基于硬判决序列,可计算相应的伴随式信息向量s=zHT=(s0,s1,…,sm-1),其中第i 个伴随式计算如下:
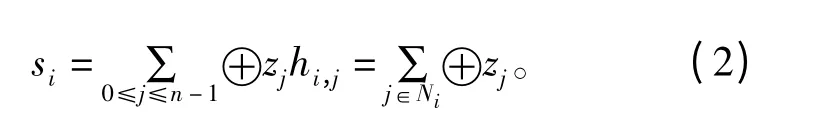
式中,记号⊕表示模2 加运算。RBI-MLGD 算法主要由三个步骤组成。
(1)校验节点信息处理
在译码过程中,使用了一种特殊的外信息。第i个校验节点Ci传递给第j 个变量节点Vj的外信息σi,j计算如下:
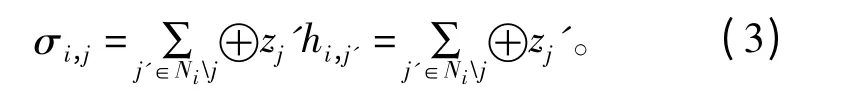
式中,0≤i≤m-1,0≤j≤n-1。
(2)变量节点信息处理
基于上述外信息,可计算与第j 个变量节点Vj相对应的总外信息
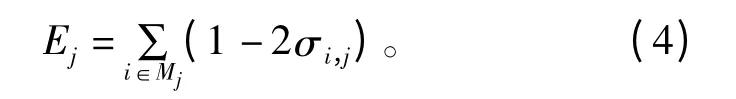
式中,0≤j≤n-1。
(3)迭代更新
令R(k)j表示第k 次迭代过程中变量节点Vj的信息可靠度,其迭代更新规则为
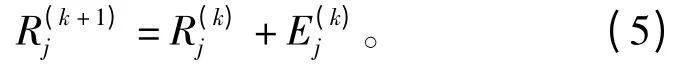
式中,0≤j≤n-1。注意,初始的可靠度设置为接收信号的量化信息,即R(0)j=qj。
4 联合星座和伴随式的算法设计
由上述译码过程可知,外信息与伴随式信息以及当前码位信息存在如下关系:

在当前伴随式si正确的条件下,校验节点回传到变量节点的外信息σi,j取值正好与zj的取值相一致。相应地,在变量节点的总外信息处理和设计时,也需要使用与当前硬判决信号zj调制方向一致的修正偏移处理。对于RBI-MLGD 算法,其发送端星座映射为φS(cj)=1-2cj,则可靠度修正应设计为φS(σij)=1-2σij,偏移方向与发送端映射规则一致,偏移幅度为1 个单位。然而,在实际应用中发送端的调制模式与信号星座的映射规则φS(.)具有多种形式。例如,当发送端映射规则改为φS(cj)=2cj-1 或其他形式时,则上述RBI-MLGD 算法基于1-2σij的修正偏移操作正好相反(其修正方向与当前信号星座信息不相符)。对于多元调制的信号星座图,其映射规则会更加复杂。基于此,为了方便算法描述,本节联合具体的星座信息对译码算法进行描述和设计。此外,我们注意到,根据σi,j的定义,校验节点回传到变量节点的外信息都是不一样的,需要单独计算,这必然会引入运算消耗,增加译码复杂度。因此,本文将不用外信息σi,j而改用伴随式信息进行算法设计。
(1)校验节点信息处理
第i 个校验节点Ci传递给第j 个变量节点Vj的信息直接使用与Ci对应的伴随式信息si。与使用外信息σi,j不一样,这时从Ci传递出来的信息都是一样的,不需要其他额外的计算。
(2)变量节点信息处理
相应地,变量节点也使用伴随式信息进行总信息的收集和处理,第j 个变量节点Vj收集到的译码信息设计如下:
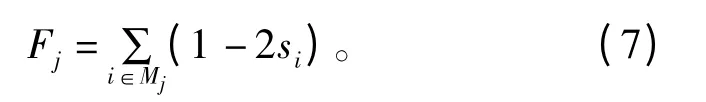
式中,0≤j≤n-1。
(3)迭代更新
令R(k)j表示第k 次迭代过程中变量节点Vj的信息可靠度,则迭代更新规则更改为
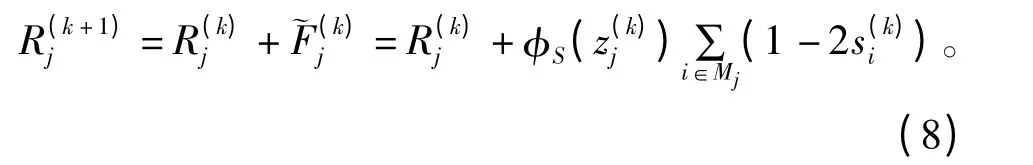
值为σi,j=zj,5 个外信息取值为σi,j=,则(1-2zj)。因此,本文提出的算法在变量点的处理与RBI-MLGD 算法是一致的,但本文在校验节点不使用外信息,避免了相应的计算操作,降低了译码复杂度。
5 复杂度分析和实验仿真
5.1 译码复杂度
本文算法的译码复杂度主要由以下几个方面产生:第一,根据公式(1),需要n 次逻辑操作计算硬判决序列;第二,根据公式(2),需要m(ρ-1)次逻辑操作计算伴随式序列;第三,计算修正的总信息需要n(γ-1)次整数加法运算和n 次逻辑运算;第四,计算变量节点的可靠度迭代更新需要n 次整数加法。综上所述,完成本文算法的一次迭代产生的总运算量为mρ +2n-m =nγ +2n-m 次逻辑运算以及nγ 次整数加法运算(mρ=nγ 是H 中非零元个数)。表1给出了本文算法一次迭代产生的计算量。由表可见,与RBI-MLGD 算法相比,本文算法每次迭代可节省mρ-n =n(γ-1)次逻辑操作,降低了译码复杂度。

表1 算法每次迭代的运算量比较Table 1 Computational complexities required per iteration
5.2 译码性能
由前面的分析可知,本文算法在迭代更新过程中对可靠度信息的处理(偏移幅度/方向)效果是一致的。因此,理论上本文算法的性能应该与RBI-MLGD 一致,不会有任何性能损失。为了方便比较,本文仍然使用文献[4]中基于有限域方法构造的(961,721)规则准循环LDPC 码以及基于二维Euclidean 几何方法构造的(4095,3367)规则循环LDPC 码作为仿真例子。同时,量化参数、最大迭代次数等仿真参数都与文献[4]保持一致。仿真结果见图1~4。由图可见,本文算法保持了RBI-MLGD算法优良的译码误码率(Bit Error Rate,BER)性能以及快速的译码收敛速度,相应的曲线几乎是重叠的(细微差别来自于仿真中所用到的随机序列)。
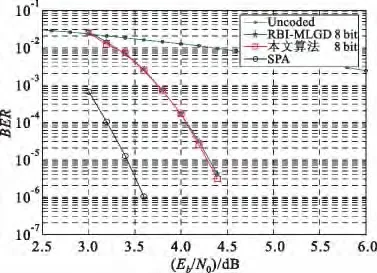
图1 (961,721)LDPC 码性能Fig.1 Performances of the(961,721)LDPC code
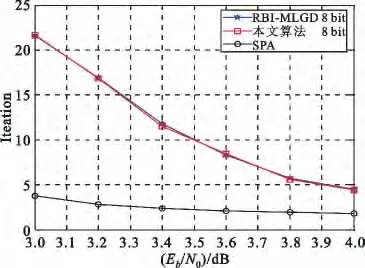
图2 (961,721)LDPC 码收敛速率Fig.2 Decoding convergence rate of the(961,721)LDPC code

图3 (4095,3367)LDPC 码性能Fig.3 Performances of the(4095,3367)LDPC code

图4 (4095,3367)LDPC 码收敛速率Fig.4 Decoding convergence rate of the(4095,3367)LDPC code
6 结束语
本文联合信号星座和伴随式信息,提出了一种基于可靠度的迭代大数逻辑译码算法。在校验节点,译码算法直接使用伴随式信息进行传递和处理;在变量节点,结合信源端的星座映射和伴随式进行可靠度信息的偏移方向和偏移幅度设计。由于本文算法使用了伴随式信息,避免了迭代过程中频繁的外信息计算操作。仿真结果表明,本文提出的算法在保持优良译码性能以及快速译码速度的同时,具有更低的译码复杂度。此外,我们指出两点:一是在译码过程中引入信号映射信息使得算法具有更好的普适性,但系统并不会因此得到额外的性能增益;二是与RBI-MLGD 算法一样,本文算法仅对列重较大的LDPC 码有效,对于随机构造的小列重码,其译码性能有待进一步提高。
[1] Gallager R G. Low density parity check codes[J]. IEEE Transactions on Information Theory,1962,8(1):21-28.
[2] Kou Y,Lin S,Fossorier M P C. Low- density parity-check codes based on finite geometries:A discovery and new results[J]. IEEE Transactions on Information Theory,2001,47(2):2711-2736.
[3] 刘原华,张美玲. LDPC 码的改进迭代比特翻转译码算法[J].电讯技术,2012,52(4):488-491.LIU Yuanhua,ZHANG Meiling.An improved iterative bit-flipping decoding algorithm for Low-density Parity-check Codes[J]. Telecommunication Engineering,2012,52(4):488-491.(in Chinese)
[4] Huang Qin,Kang Jingyu,Zhang Li,et al. Two reliability based iterative majority logic decoding algorithms for LDPC codes[J]. IEEE Transactions on Communications,2009,57(12):3597-3606.
[5] Chen C Y,Huang Q,Kang J Y,et al.A binary messagepassing decoding algorithm for LDPC codes[C] //Proceedings of 47th Annual Allerton Conference. Illinois:IEEE,2009:424-430.
[6] Chen H,Zhang K,Ma X,et al. Comparisons between reliability-based iterative min-sum and majority logic decoding algorithms for LDPC codes[J]. IEEE Transactions on Communications,2011,59(7):1766-1771.
[7] Ngatched T M N,Alfa A S,Cai J. An improvement on the soft reliability- based iterative majority- logic decoding algorithm for LDPC codes[C] //Proceedings of 2010 IEEE Global Telecommunications Conference. Miami:IEEE,2010:1-5.
[8] Zhang K,Chen H,Ma X. Adaptive decoding algorithms for LDPC codes with redundant check nodes[C]//Proceedings of 2012 IEEE International Symposium on Information Theory(ISIT). Gothenburg:IEEE,2012:175-179.
[9] Ma X,Zhang K,Chen H,et al.Low complexity X-EMS algorithms for non-binary LDPC codes[J]. IEEE Transactions on Communications,2012,60(1):9-13.

