采用延时积分的MSK 软判决解调方法*

闫 涛，张大鹏，陶 祁

(1.空军第一航空学院 航空电子工程系，河南 信阳464000;2.解放军95883 部队，北京102206)

1 引 言

作为一种较为先进的数字通信信号调制方式，最小频移键控(Minimum Shift Keying，MSK)具有包络恒定、相位连续、频带利用率高、带外辐射功率小等优点［1］，在现代通信系统特别是军事通信中得到了广泛的应用。

和其他数字调制方式相同，在实际的应用中，MSK 调制往往和信道编码技术相结合以获得较好的系统抗噪声和抗干扰性能。传统的分组编码和卷积码在译码过程中需要解调输出的硬判决信息，MSK 按照常规的硬判决解调方法即可满足要求。然而，随着Turbo 码的提出，迭代译码的思想在信道编译码技术领域内得到了广泛运用，软判决解调以其信息量损失小、对系统性能提升较大获得一致认可，因此，MSK 信号的软判决解调成为其应用于软输入软输出(Soft Input Soft Output，SISO)迭代译码系统中需要解决的核心问题。

MSK 是一种连续相位调制(Continuous Phase Modulation，CPM)，其调制过程可分解为连续相位编码器(Continuous Phase Encoder，CPE)与无记忆调制器(Memoryless Modulator，MM)的级联，可以看作是码率为1 的卷积码和无记忆调制器的组合［2］，因此，MSK 的调制过程可以使用网格图来描述，其最优的软判决解调方法一般采用最大似然序列估计(Maximum Likelihood Sequence Estimation，MLSE)检测Viterbi 算法［3］和逐符号最优的最大后验概率(Maximum a Posteriori Probability，MAP)检测算法［4］，借助反馈迭代译码构成软输入软输出的迭代检测系统。这两种方法虽然可以获得比较优异的性能，但是算法复杂度较高、延时较大，同时，由于编码调制的一体化设计，上述两种MSK 软判决解调算法的通用性和灵活性较差。

文献［5］根据MSK 信号的特点提出了符号提取与幅度加权相结合的MSK 软差分解调算法，适用于MSK 调制与各种软判决译码串行级联，具有较强的通用性，但是文献中并未给出相关的理论依据，并且其实现方法相对复杂。

本文在深入研究MSK 延迟判决解调方案的基础上，根据条件概率的相关理论，结合对数似然比信息的定义提出了一种基于延迟积分的MSK 信号软判决解调方法。仿真与分析结果表明，与文献［5］给出的幅度加权差分解调算法相比，该方法简单方便，在Turbo+MSK 编码调制系统中应用能够获得更加优异的抗噪声性能。

2 MSK 调制原理及其延时判决解调

MSK 信号在第k 个码元内的波形可表示为［6］

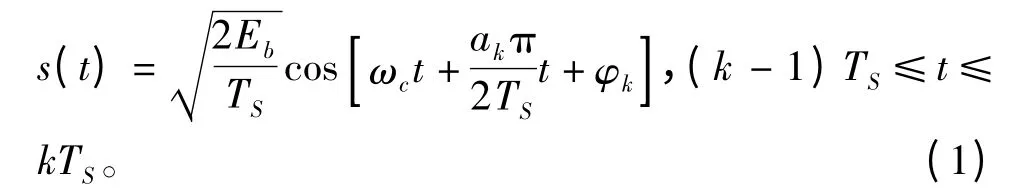
式中，ωc=2πfc为载波角频率;ak= ±1(当输入码元为“1”时，ak= +1;当输入码元为“0”时，ak=－1);Eb为码元能量;TS为MSK 信号的码元宽度，为分析方便，这里将信号幅度进行归一化处理，即为第k 个码元的初始相位，φk=0 或π，它在一个码元宽度中是不变的，它不仅与当前的输入ak有关，还与前一码元的相位φk－1和ak－1相关。

MSK 信号可以使用同相和正交两个分量表示:

式中，右端第1 项称作同相分量，其载波为cosωct;第2 项称作正交分量，其载波为sinωct;pk和qk为包含输入码元信息的±1 序列，不妨将其称之为同相码元和正交码元，其中pk= cosφk，qk= akcosφk=akpk。根据这一特性，MSK 调制信号可以通过对输入码元信息进行差分编码的方式产生，如图1所示。

图1 基于差分编码的MSK 调制信号产生方框图Fig.1 Block diagram of the MSK transmitter with differential encoding

由图1可以看出，输入码元序列{ak}经过差分编码即可获得同相码元和正交码元，经载波调制后即可获得MSK 信号。

由于MSK 本质上是一种码元波形严格正交的2FSK 调制，因此在接收端可以沿用2FSK 的相干解调和非相干解调完成调制信号的恢复。除此之外，根据MSK 信号附加相位连续变化的特性，接收端也可以采用延时判决相干解调，其结构如图2所示。

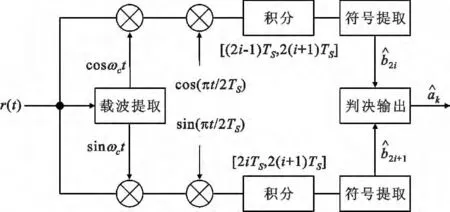
图2 MSK 信号的延迟判决解调方框图Fig.2 Block diagram of the MSK receiver with time－delay－decision demodulation scheme

首先，从受噪声污染的MSK 信号r(t)提取载波，然后将其与r(t)分别按照“同相”和“正交”两路进行相关运算，完成相干解调，并将运算结果进行低通滤波后在两个码元周期即2Ts内完成积分，最后提取符号并根据符号的异同判决输出原调制码元信息，判决输出的过程实际上是解差分过程。

3 采用延时积分的MSK 软判决解调方法

MSK 的延时判决解调利用了前后两个码元的信息对前一码元作判决，因此可以提高数据的可靠性。但是，延迟判决解调输出的是码元的硬判决信息，其结果不能直接用于软输入软输出的迭代译码系统。为了获得MSK 信号的软解调信息，需要对MSK 信号的延时判决解调方案进行改进。

在延迟判决解调方案中，解调器将接收到的信号r(t)分成两路处理，分别从中恢复出原调制信号中的同相码元和正交码元的硬判决信息，最后按照这两路信息完成解差分过程。要获得软判决信息，可以对同相和正交两路信号不作判决，直接使用积分结果作为解调的软输出，但如何通过这两路软输出信号进行“软差分”最终获得MSK 信号的软判决解调信息是一个值得研究的问题，也是实现MSK 信号软输出的关键。本文试图从具有差分关系的调制码元着手进行分析。

由于差分编解码只是两个相邻码元存在关联，为了简化分析，考虑两个相邻时刻的信号调制和解调情况，这里仅在理想抽样条件下进行分析。假设xk－1为MSK 调制器k－1 时刻的抽样输出，由于差分的关系以此作为参考信号，k 时刻调制器输出可表示为xk=ψkxk－1，其中ψk= ±1，不妨定义为差分编码系数，其取值取决于k 时刻和k－1 时刻输入码元的关系。在AWGN 信道中，经过噪声污染后对应接收端的信号可以表示为

式中，ρ 为信噪比，ωk、ωk－1均为服从N(0，1)分布的高斯离散白噪声。若对于式(3)两端同乘以ψk，则有

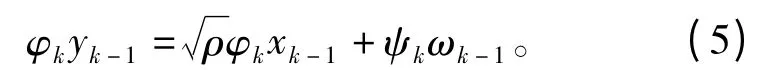
将xk=ψkxk－1代入式(4)，得

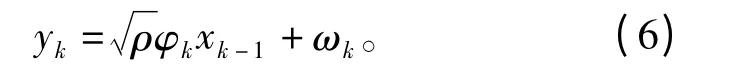
综合式(5)和式(6)可得

显然，式中ω'k=ωk－ψkωk－1，服从N(0，2)分布，其均方差σ2n=2。在Turbo 译码过程中，输入SISO 译码器的是关于信息比特的对数似然比信息，我们不妨考察yk关于差分编码系数ψk和前时刻接收信息yk－1的条件概率密度函数(PDF)

根据对数似然比的定义，不难计算并化简得到对数似然比

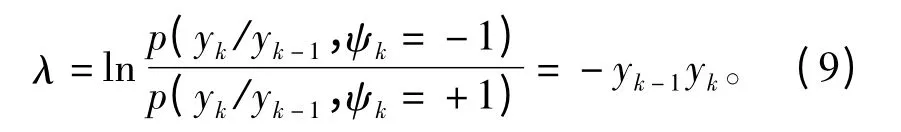
由上述分析可知，该对数似然比表征了k 时刻输入MSK 调制器信息码元的软判决度量，可以看出，MSK 信号软信息等于当前码元软判决信息yk与前一码元软判决信息yk－1乘积的相反数。根据这一关系，本文在MSK 延迟解调方框图的基础上给出MSK 信号软信息获取方法，如图3所示。

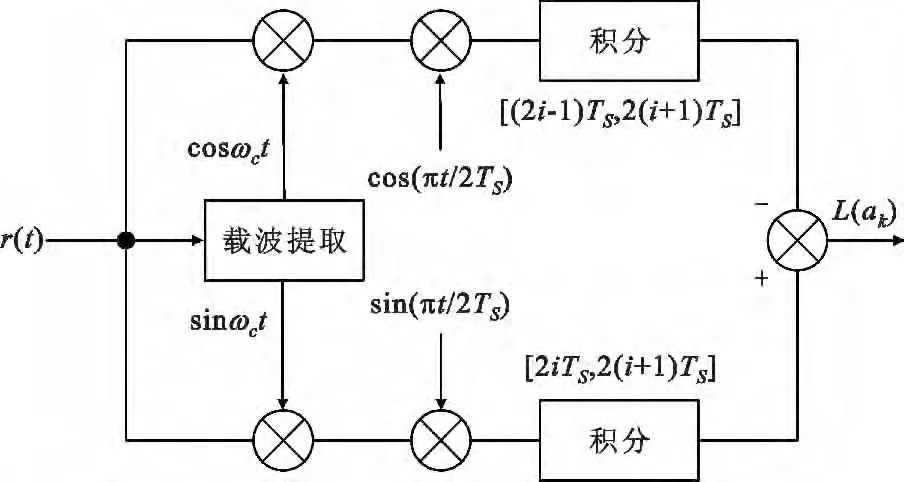
图3 MSK 信号软判决解调框图结构Fig.3 Block diagram of soft－decision demodulation for MSK signal

受噪声污染的MSK 信号经过如图3中的载波提取、相关运算、延迟积分等过程分别获得同相和正交分量的软判决度量。由于在此过程中只进行了线性运算，因此积分器输出同相分量和正交分量的软判决度量可认为是调制器输出的码元信息与高斯白噪声的叠加，即在解调过程中，我们可以将图3中接收端同相和正交两条支路的积分器输出信号等效为式(3)和式(4)中的yk－1和yk，这样，按照式(9)计算的对数似然比信息可以表征调制MSK 信号的二进制信息码元的最大后验概率之比。

4 性能仿真与分析

为验证采用延时积分MSK 软判决解调方法的有效性和可靠性，将其与Turbo 码系统级联构成Turbo 联合MSK 编码调制系统，采用Le. Goff 提出的BITCM 系统构造方案［6］，将MSK 软信息也即二进制信息比特的对数似然比信息直接输入标准的二元Turbo 译码器进行迭代译码。

为方便对比，与文献［5］相同，按照第三代移动通信标准(3GPP)的相关参数进行设置，选取(13，15)RSC 码作为Turbo 码的分量编码器，使用3GPP伪随机交织器，两个成员译码器的译码算法采用Max－Log－MAP 算法，设置迭代译码次数为6 次，信息帧长分别选取512 bit 和1024 bit，系统的误码率(Bit Error Rate，BER)曲线分别如图4(a)和(b)所示，图中幅值加权法的系统误码率数据来自于文献［5］给出的系统性能曲线。

由图4可以看出，采用延时积分的软判决解调方法能够为Turbo 联合MSK 的编码调制系统带来更加优异的BER 性能，相对于文献［5］给出的性能最优的幅值加权法，其对系统性能的提升至少0.5 dB。分析原因在于，本文提出的软判决解调方法获取的是二进制信息比特的对数似然比信息，其理论依据源自于最大后验概率译码算法，可靠性和信用度相对较高;而文献［5］给出的MSK 软解调信息仅仅停留在不作判决的信号幅度这一层面上，虽然形式上是软判决结果，但其信息有用性相对较弱。

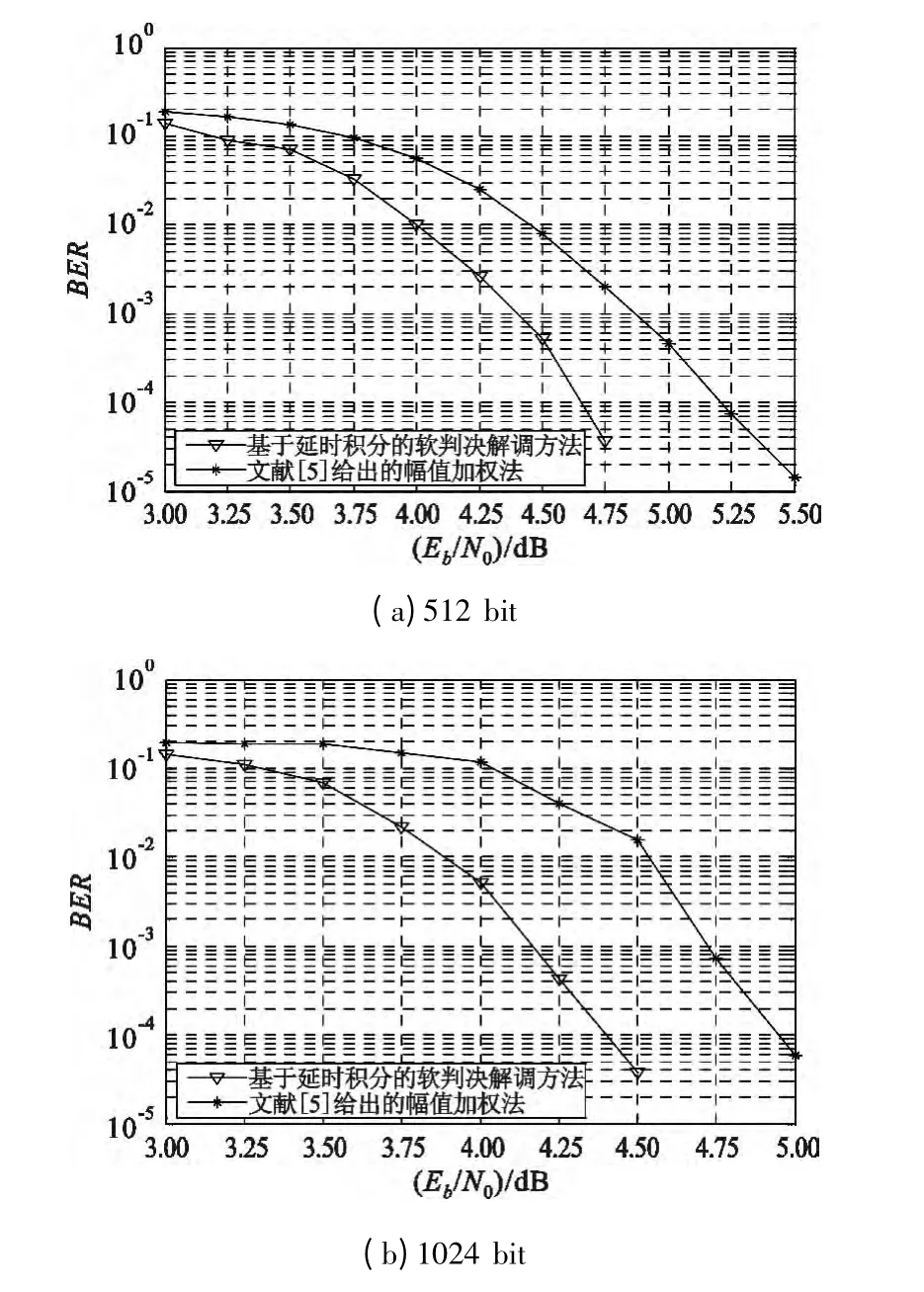
图4 基于延时积分软判决解调和幅值加权法的Turbo 联合MSK 编码调制系统BER 性能比较Fig.4 BER comparison between Turbo coded MSK systems respectively using time－delay soft decision demodulation method and amplitude weighting scheme in the receiver

与幅值加权法相同，基于延时积分软判决解调方法不需要通过迭代检测获得信息码元的软信息，虽然在一定程度上损失了性能，但是由于接收端解调和译码具有一定的独立性，在应用时更加灵活，适用于同时嵌入多种编码和调制方式的软件无线电系统。另外，从实现复杂度来看，基于延时积分软判决解调只需将同相分量和正交分量的积分度量相乘即可，相比幅值加权法的符号提取、差分译码、取绝对值等处理步骤大大简化。

5 结束语

由于调制过程中差分编码的引入使得MSK 信号的软判决信息不易获取。本文针对MSK 的软判决解调提出一种简单有效的计算方法，该方法可看作是MSK 延迟判决解调方案的改进，具体实现过程是:对延迟判决解调方案中接收MSK 信号的同相分量和正交分量不作判决，将其延迟积分度量等效为解调器输出码元与离散高斯白噪声的叠加，根据条件概率的相关理论推导，MSK 信号的软判决信息最终可以表示为同相分量和正交分量的乘积。仿真与分析结果表明，该软判决解调方法简单有效，在MSK 联合Turbo 编码调制系统中验证具有较好的抗噪声性能，在相同的仿真条件下，相比已提出的同类软解调算法至少有0.5 dB的增益。进一步验证该软判决解调方法是否同样适用于MSK 与其他软输入软输出迭代译码构成的编码调制系统，是下一步需要研究的问题。

［1］ Pasupathy S. Minimum shift keying:a specially efficient modulation［J］. IEEE Communications Magazine，1979，17(7):14－22.

［2］ Victor F S，Subbarayan P. Iterative decoding of serially concatenated convolutional codes and MSK［J］. IEEE Communications Letters，1999，3(9):272－274.

［3］ Par M，Tor M A. Serially concatenated continuous phase modulation with iterative decoding［J］.IEEE Transactions on Communication，2001，49(11):1901－1915.

［4］ Michael J G，John H L. Symbol－by－symbol MAP demodulation of CPM and PSK signals on Rayleigh flat－fading channels［J］. IEEE Transactions on Communications，1997，45(7):788－799.

［5］ 赵旦峰，朱铁林，薛睿.迭代译码系统中差分MSK 软解调算法［J］.计算机工程与应用，2011，47(27):129－131.ZHAO Danfeng，ZHU Tielin，XUE Rui.Soft demodulation algorithm of differential MSK iterative system［J］. Computer Engineering and Applications，2011，47(27):129－131.(in Chinese)

［6］ Goff S L，Glavieux A，Berrou C. Turbo－codes and high spectral efficiency modulation［C］ //Proceeding of 1994 IEEE International Conference on Communications. New Orleans，USA:IEEE，1994:645－649.