采用改进ML－OSIC 的MIMO 联合检测*

刘 晶

(华北计算技术研究所，北京100083)

1 引 言

多输入多输出(Multiple－ input Multiple－ output，MIMO)技术的目的是为了更大程度提高信道容量而使用多根发送天线和接收天线同时进行数据传输的无线通信技术，与传统的单输入单输出(Single Input Single Output，SISO)技术相比，在不增加额外发送功率和带宽的情况下，具有Nt根发送天线和Nr根接收天线的MIMO 系统可以获得min(Nt，Nr)的信道增益。广义的MIMO 技术包含发射分集技术和空间复用技术两类，前者以增强信号可靠性为目的，利用多路径传输来对抗信道衰落带来的影响;后者同时发送并行数据流，并且在接收端对接收到的信号进行分别处理。分层空时码是空间复用技术的典型应用，特别是垂直分层空时码［1］(V－BLAST)。

V－BLAST 检测算法(即ZF－OSIC 检测算法)是一种广泛熟知的非最优检测算法，非最优的性能是由于迫零运算(nulling operation)导致的噪声增强和已检测层的干扰消除所造成的误差传播造成。而空间复用多输入多输出(Space Multiplexing MIMO，SM－MIMO)系统的信号检测算法中，最佳检测——最大似然(Maximum Likelihood，ML)算法因其复杂度随着调制阶数和天线数目的增加呈指数增长，这种穷尽搜索方式在实际系统中难以实现。文献［1］中基于ML－DFE 算法［2］提出了一种次优的联合检测算法——ML－ OSIC，避免了层间干扰和误码扩散，这种算法虽然改善了检测性能但其算法复杂度仍然偏高［3］。文献［4］中，笔者针对V－BLAST 系统中由于连续检测造成的错误传播效应，提出了基于最小均方差(Minimum Mean Square Error，MMSE)的迭代译码算法。Lamare［5］在决策反馈接收机中提出了迭代的连续与并行干扰消除构架和近优的低复杂度排序算法。

传统OSIC 检测算法的复杂度大部分是由于伪逆运算而造成的［6］，笔者采用并行检测后精确检测值的方式取代原始的逐层检测方式，大幅度降低矩阵求逆的运算量。以往关于ML－OSIC 联合检测算法的研究工作中，并没有针对执行ML 算法的层数对整体复杂度和性能造成的影响进行详细分析，笔者针对ML 算法参与的检测层数对整体复杂度的影响，提出一种将复杂度和性能联合折衷的处理方案，即通过最优复杂度公式的计算，优先选择出b 层来进行改进的连续干扰消除算法，其余的累积了误码扩散的信号层我们使用ML 检测来提高性能。实验结果表明，改进的算法可以在远低于ML 复杂度的基础上获得次优的译码性能。

2 系统模型与改进的OSIC 检测算法

2.1 系统模型

考虑一个未编码系统，Nt个节点同时发送信息，在接收端有Nr根接收天线，时刻i 接收到的离散信号可表示为

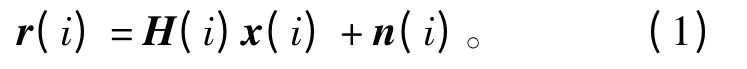
式中，H(i)是Nr×Nt复衰落系数矩阵，矩阵中的第(r，t)元素用［H(i)］r，t 表示，代表了在时刻i 上第r个接收节点到第t 个发送节点间的信道衰落系数值;r=［r1，r2，…，rNr］表示Nr根接收天线上收到的信号是Nt根发送天线发射信号x =［x1，x2，…，xNt］经过信道传输后再叠加并伴有高斯白噪声的干扰;n(i)是Nr维接收信号向量，各矢量元素是独立且均值为0 的高斯随机变量，其实部虚部都独立，且方差均为N0/2。

2.2 传统OSIC 检测算法

传统的OSIC 检测算法是优先检测错误概率最小层的信号，将所选的最小层信号当作干扰信号在接收端消除，通过逐次迭代，最终完成所有信号向量的检测。下面介绍具体的ZF－OSIC 算法。

初始化:令r1=r，H1=H，i=1。

(1)计算第i 次的迭代加权矩阵，令加权矩阵

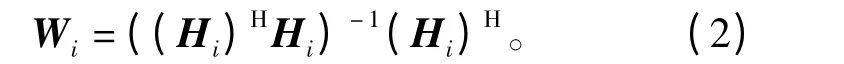
(2)计算表示信噪比最大的符号所对应的序列号μi:

(5)接收端剔除所选层信号带来的干扰，计算

然后将Hi从H 中删除，得到矩阵Hi+1。

(6)令i=i+1，返回到第1 步。

其中 ()，·H表示埃米特转置操作;Hi表示从H 中去掉hμ1，hμ2，…，hμi－1等列后得到的n×(m－i+1)维矩阵，其中i=2，3，…，m;μi是加权矩阵Wi中最小Frobenius 范数的行序号，Q(·)函数根据星座图对各层检测出的信号进行硬判决解调。传统OSIC 算法由于多次计算矩阵的广义逆，导致复杂度高［7］。

2.3 改进的OSIC 算法

改进的OSIC 算法的目的是在维持相对满意性能的前提下，减少伪逆运算的次数。该算法首先利用并行检测方案，“粗”估计一组信号，再利用前项消除和后项消除的方式来精确“粗”估计后的结果。下面介绍算法步骤。

初始化:令r1=r，H1=H，i=1。

假设H 是n×m 阶矩阵，将n 层信号合并检测，进行“粗略”估计:

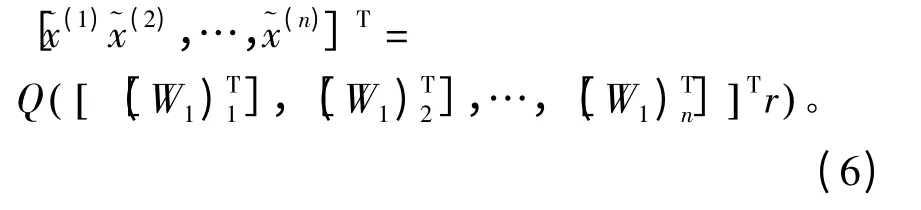
式(6)是一组粗略检测值，为使得检测值精确，我们可以消去层间的相互干扰，定义参数j，令j=0，1，2，…，n－1，计算

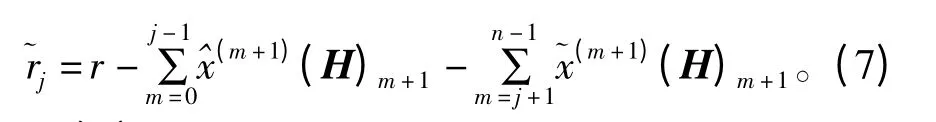
式(7)可以被看作改进的并行干扰消除算法。等号右边的第二项执行了后相消除的功能，这是由于，m=0，1，…，j－1 是当前已经检测出来的信号;等号右边第三项执行了前向消除的功能，这是由于，m =j +1，j +2，…，n－1 是未被检测出的信号，即公式(6)中“粗略”估计出来的信号。最终得到检测信号为

3 改进的ML－OSIC 检测算法

在改进的连续干扰相消算法中，如果并行检测运算带来的微小性能损耗可以容忍，那么新算法将会大大减少计算复杂度。本节中，我们将改进的连续干扰相消算法进一步与ML 检测算法相结合，并通过推导的复杂度公式提出一种改进的ML－OSIC检测算法，使其在性能与复杂度上具有良好的折衷。

3.1 算法描述

改进的ML－OSIC 算法是将2.3 节中推导的改进的OSIC 算法与ML 算法相结合，具体算法如图1所示，下面介绍相应的算法。

初始化:令r1=r，H1=H，i=1

(1)利用复杂度公式(3.2 节详细描述)选择b层进行改进的连续干扰相消。利用公式(6)对所选的b 层信号进行“粗略”估计:

(2)消去b 层间相互干扰，将粗略估计值进一步精确化，定义j，令j=0，1，2，…，b－1，计算

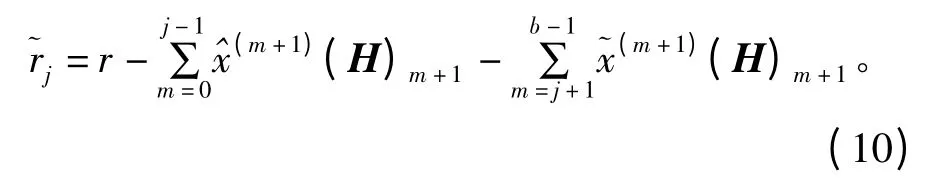
(3)检测到的信号为

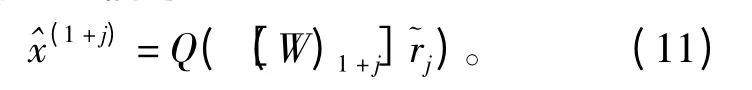
(4)消除b 层已检信号在接收端带来的干扰:

(5)对于未检测层信号，我们继续采取ML 检测方式:

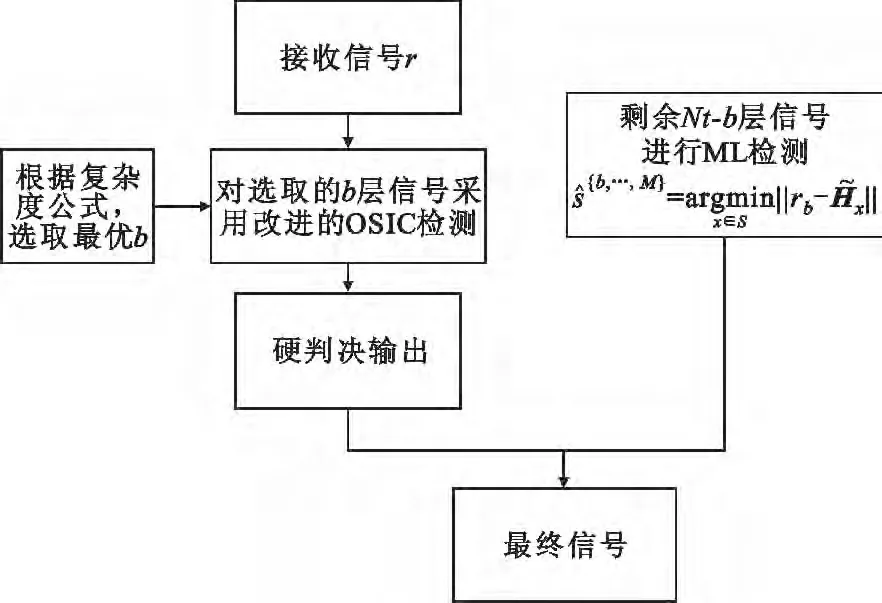
图1 改进的ML－OSIC 检测框图Fig.1 Block diagram of the modified ML－OSIC detection

3.2 复杂度分析与最优值b 的选择

ML 算法需要对SN个向量进行遍历搜索，具有指数增长的复杂度。OSIC 较ML 算法能大幅减少计算量，但仍需进行4M2+2NM2次伪逆运算，其中每一次迭代运算的M 值是变化的。此外，传统OSIC 还需要2MN +(N－1)M +MN 次排序和干扰相消运算。改进的ML－OSIC 算法在复杂度与性能间折衷，我们假设b 层进行并行相消剩下的(M－b)层进行ML 检测，表1是各算法复杂度的比较［8］。

表1 各算法复杂度比较Table 1 Complexity comparison among ML，ZF－OSIC and improved ML－OSIC

表2比较了不同调制方式时各算法所需的算法复杂度。可以看出，对于改进的ML－OSIC 算法，总有一个最优的b 值使得算法复杂度最小。

表2 不同调制方式下的复杂度(4×4)Table 2 Complexity comparison among 16 QAM，QPSK and BPSK modulation modes(4×4)

4 仿真结果及分析

4.1 仿真环境

使用Matlab 仿真平台，仿真系统为4 发4 收MIMO 系统，发送端发送［0，1］序列，信道为准静态瑞利平坦衰落信道，信道矩阵元素的实部和虚部是独立同分布的复高斯随机变量，噪声是高斯白噪声。总发射功率P =1，每根天线上的噪声平均功率为N=P×10SNR/10，信噪比(SNR)范围为0～30。图2采用的是QPSK 调制方式，根据表2，选择出b=3 层进行改进的连续干扰消除算法，设定发送符号数为10 000。同理，图3采用BPSK 调制方式，参考表2，选择出b=2 层进行改进的连续干扰消除算法，设定发送符号数为10 000。分别用ZF－ OSIC、改进的ML－OSIC 和ML 算法进行译码检测，最后以SNR(单位dB)为横坐标绘出的误比特率曲线。

4.2 仿真结果分析

图2和图3分别给出了BPSK 和QPSK 调制下利用选定的最优b 层信号分别进行改进ML－OSIC算法、传统的ZF－OSIC 算法、ML 算法在4×4 MIMO 系统中的误码率性能比较。从图中我们可以看出，ML 检测方式的性能在三者中是最好的，传统ZF－OSIC 性能是三者中最差的，改进的ML－OSIC 算法性能介于两者之间。换句话说，文中提出的改进ML－OSIC 算法性能优于传统的OSIC 算法。结合图2和图3还可以看出:在仿真条件都相同的前提下，不同的调制方式下得到的系统检测性能不同。

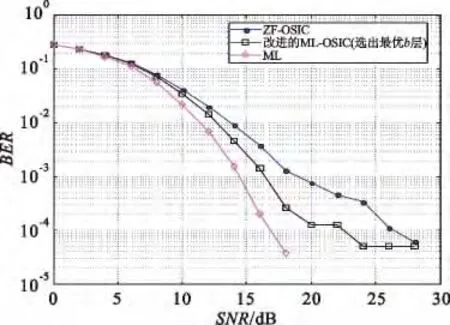
图2 QPSK 调制下不同检测方式误码率对比Fig.2 BER comparison between proposed and conventional schemes with QPSK modulation

图3 BPSK 调制下不同检测方式误码率对比Fig.3 BER comparison between proposed and conventional schemes with BPSK modulation

表3给出了在BPSK 和QPSK 调制下不同检测算法的仿真时间对比，可以看出，在BPSK 调制下，ML 检测的算法复杂度小于ZF－OSIC 算法复杂度，其原因是ZF－OSIC 检测具有大量的矩阵求逆，而ML 检测算法则不需要矩阵求逆。然而，本文提出的改进的ML－OSIC 算法的仿真时间却小于ML 检测和ZF－OSIC 检测，这是由于改进算法所选择的最优层数很好地避免了ZF－OSIC 检测模块的大量矩阵求逆和ML 检测的搜索。此外，改进的算法得到了更优的系统性能。因此，本文提出的算法不仅运算量大大降低而且得到了优于ZF－OSIC 算法的性能。

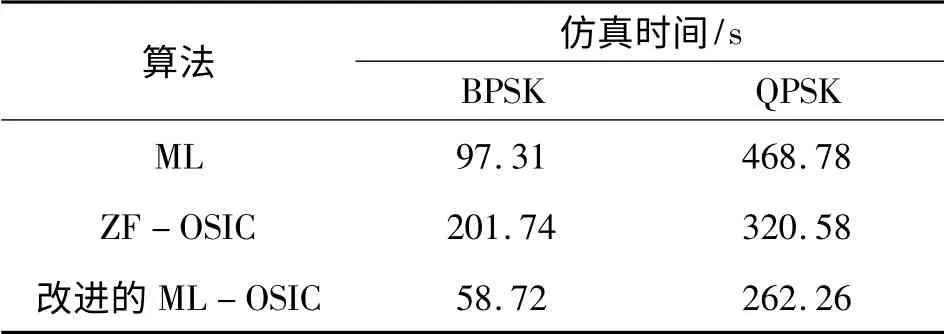
表3 BPSK 与QPSK 下不同检测方式仿真时间对比Table 3 Simulation time comparison between BPSK and QPSK modulation

5 结束语

本文考虑到传统OSIC 算法的缺陷，将连续干扰消除算法与ML 算法相结合作为译码系统的基本构架。为简化OSIC 算法复杂度，本文首先提出改进的连续干扰消除策略代替传统的连续干扰消除算法，该算法利用并行“粗”检测，再精确其检测值，大大减少了伪逆矩阵的计算次数。以往学者的研究工作并没有研究ML 算法层数对整体算法造成的影响，而本文接着以复杂度最低化为依据，将改进的连续干扰消除算法与ML 算法以最优方式相结合，构造了新型ML－OSIC 算法。性能仿真表明，该算法性能接近最佳检测，符合系统实时的要求，同时复杂度相较于ML 和传统ZF－OSIC 算法是最小的。该算法在更多天线配置及其高阶调制下会有更大的优势。

［1］ 汪蓓，朱琦.MIMO－OFDM 系统中一种改进的V－BLAST检测算法［J］.信号处理，2009，25(9):1409－1413.WANG Bei，ZHU Qi. An Improved Algorithm for V－BLAST Detection in MIMO－ OFDM System［J］. Signal Processing，2009，25(9):1409－1413.(in Chinese)

［2］ Choi Won－ Joon，Negi R，Cioffi M. Combined ML and DFE decoding for the V－BLAST system［C］//Proceedings of 2000 IEEE International Conference on Communications.New Orleans，LA:IEEE，2000:1234－1248.

［3］ 张端金，赵金平，蒋静.ML－OSIC 检测的快速递归算法［J］.郑州大学学报(工学版)，2011，32(1):107－111.ZHANG Duanjin，ZHAO Jinping，JIANG Jing.Fast Recursive Algorithm for ML－ OSIC Detection［J］. Journal of Zhengzhou University(Engineering Science)，2011，32(1):107－111.(in Chinese)

［4］ Lee H，Lee B，Lee I.Iterative detection and decoding with an improved V－BLAST for MIMO－OFDM systems［J］.IEEE Journal on Select in Areas Communication，2006，24(3):504－513.

［5］ deLamare R，Sampaio－Neto R.Minimum mean－squared error iterative successive parallel arbitrated decision feedback detectors for DS－CDMA systems［J］. IEEE Transactions on Communication，2008，56(5):778－789.

［6］ Iqbal A，Islam S M R，Kwak K S.A study on the performance of UWB－ MIMO detection techniques［C］ //Proceedings of Third International Conference on Ubiquitous and Future Networks.Dalian:IEEE，2011:220－223.

［7］ Chang D C.Spatial－Division Multiplexing MIMO Detection Based on a Modified Layered OSIC Scheme［J］.IEEE Transactions on Wireless Communications，2013，12(9):4258－4271.

［8］ Maung S M，Hajima S，Iwao S. Reduced Complexity Scheme for MIMO Receiver with Combined ZF－ OSIC and ML Detection［C］ //Proceedings of 2012 IEEE Symposium on Computer and Informatics.Penang:IEEE，2012:92－96.