二维抛物型方程的高精度分支稳定隐格式

詹涌强， 杨小辉， 谭志明

(1.华南理工大学广州学院 计算机工程学院，广东 广州 510800；2.广东警官学院 计算机系，广东 广州 510440；3.广东理工职业学院 数学教研室，广东 中山 528458)



二维抛物型方程的高精度分支稳定隐格式

詹涌强1， 杨小辉2， 谭志明3

(1.华南理工大学广州学院 计算机工程学院，广东 广州 510800；2.广东警官学院 计算机系，广东 广州 510440；3.广东理工职业学院 数学教研室，广东 中山 528458)

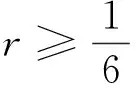
二维抛物型方程；隐式差分格式；截断误差

引 言

在渗流、扩散、热传导等领域中经常会遇到求解二维抛物型方程的初边值问题,在二维情形，其模型问题为

(1)

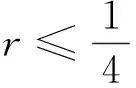
1 差分格式的构造

令Δx=Δy与Δt分别表示空间和时间方向的步长，用如下含参数的差分方程逼近微分方程(1)

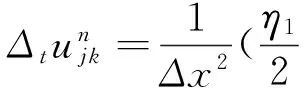
(2)

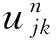
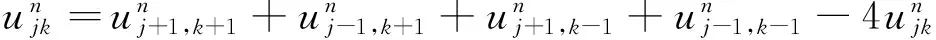
其余类推，η1～η6为待定参数，适当选择这些参数，可以使(2)逼近(1)具有尽可能高阶的误差和较好的稳定性.

当(1)的解充分光滑时，如下关系式成立

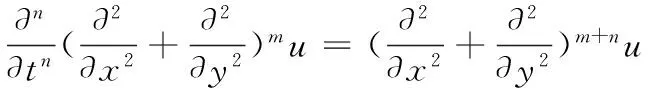
(3)

将(2)式中各节点上的u在节点(jΔx,kΔy,nΔt)处作Taylor展开，并利用关系式(3)整理可得

为了使格式(2)的截断误差达到O(Δt2+Δx4)，须满足下面方程组

(4)

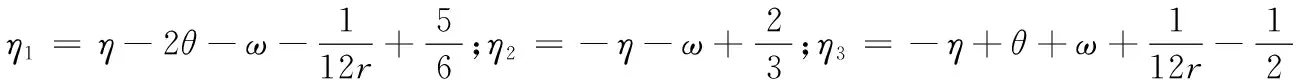
将所得各值代入(2)式，可得截断误差为O(Δt2+Δx4)的三参数三层隐式差分格式

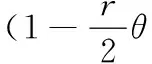
(5)

2 稳定性和收敛性

利用Fourier分析法讨论格式(5)的稳定性，首先写出与之等价的两层格式组

(6)

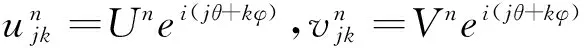
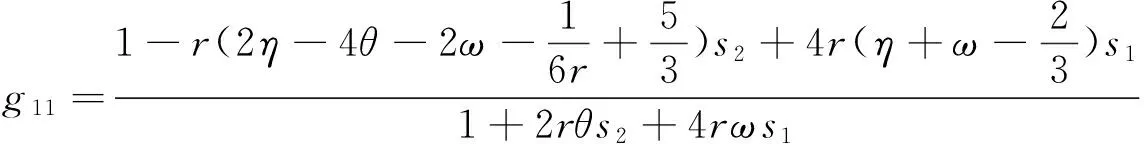
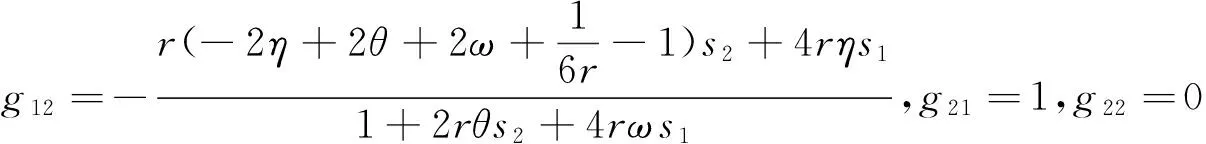
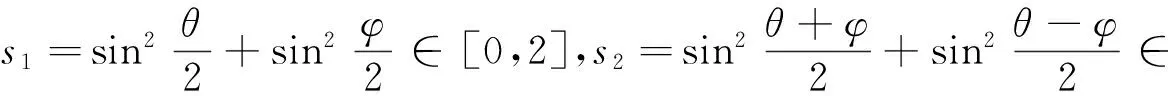
传播矩阵G(s1,s2)的特征方程为

λ2-g11λ-g12=0.

(7)

引理1[8]特征方程(7)的根满足|λ1,2|≤1的充要条件是

|g11|≤1-g12≤2.

(8)

引理2[8]差分格式(5)稳定，即矩阵族Gn(s1，s2)(0≤s1,s2≤2，n=1,2,…)一致有界充要条件是

(1)|λ1,2|≤1(λ1,2是方程(7)的两个根)；

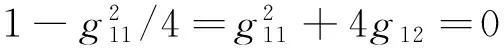
定理1 差分格式(5)稳定的一个充分条件是

(9)

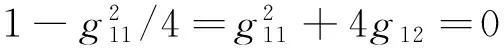
由g11≤1-g12可得

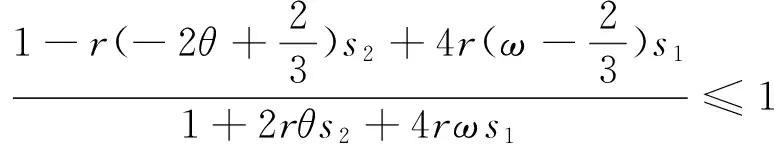
(10)

为确定起见，不妨假定

1+2rθs2+4rωs1>0，

由s1,s2的取值范围可知，该式成立的一个充分条件是

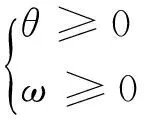
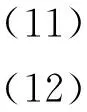
当(11)，(12)两式成立时，可验证(10)式亦成立.而当(11)，(12)两式成立时，由1-g12<2可得

(13)

(13)式成立的一个充分条件为

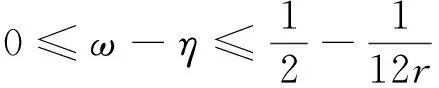
(14)

再由-1+g12≤g11

可得

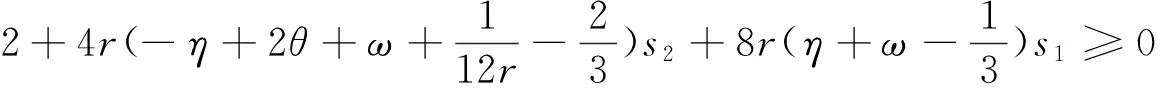
(15)

(15)式成立的一个充分条件为

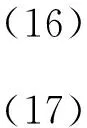
由条件(14)，可得(16)，(17)两式成立的一个充分条件为

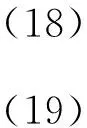
综合(11)、(12)、(14)、(18)、(19)式，由Lax的稳定性与收敛性等价定理即证得本定理.

3 参数的选取及差分格式的确定

格式(5)中的参数应按定理1的条件(9)选取，现提供如下方法：

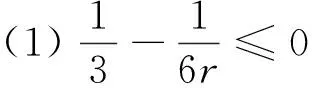
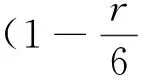
(20)

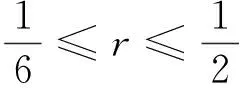
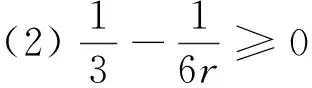
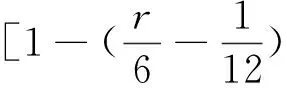
(21)

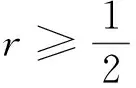
4 数值例子

对初边值问题

(22)

利用格式(20)与(21)求数值解，并与精确解进行比较.

表1 格式(20)和(21)数值解与精确解的比较

由表1可以看出，对满足稳定性条件不同的r，本文格式解与精确解均有很好的吻合，这与理论分析完全一致.

[1] 陆金甫，关治.偏微分方程数值解法[M].北京：清华大学出版社，2010：112-114.

[2] 戴嘉尊，邱建贤.微分方程数值解法[M].南京：东南大学出版社，2008：95-103.

[3] REN Zong-xiu, CHEN Zhen-zhong, WANG Xiao-feng. A family of high-order accuracy explicit difference schemes for solving 2-D parabolic partial differential equation[J]. Chinese Quarterly Journal of Mathematics, 2002,17(3)：57-61.

[4] 詹涌强，陈妙玲，谭志明.二维抛物型方程的分支稳定显式差分格式[J].暨南大学学报：自然科学与医学版，2013,34(5)：467-470.

[5] 曾文平.解二维抛物型方程的恒稳高精度格式[J].华侨大学学报：自然科学版，1999,20(1)：18-24.

[6] 马明书.二维抛物型方程的一族两层显式格式[J].河南师范大学学报：自然科学版，2002,30(1)：23-25.

[7] 马明书，申培萍，张利霞.二维抛物型方程的高精度分支稳定显格式[J].工程数学学报，1999,16(3)：139-142.

[8] 马驷良.二阶矩阵族Gn(k,Δt)一致有界的充要条件及其对差分方程稳定性的应用[J]. 高等学校计算数学学报,1980:2(2)：41-53.

A High Accuracy Implicit Difference Scheme With Branching Stability for Solving Two-Dimension Parabolic Equation

ZHAN Yong-qiang1， YANG Xiao-hui2， TAN Zhi-ming3

(1.School of Computer Engineering， Guangzhou College of South China University of Technology，Guangzhou 510800, China；2.Department of Computer, Guangdong Police College, Guangzhou 510440， China;3.Department of Mathematics Education， Guangdong Polytechnic Institute， Zhongshan 528458， China)

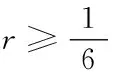
two-dimension parabolic equation; implicit difference schemes; truncation error

10.14182/J.cnki.1001-2443.2015.03.004

2014-05-10

国家自然科学基金项目(61070165)；广东省教育部产学研结合项目(2011B090400458)

詹涌强(1978-)，男，广东潮州人，硕士，讲师；研究方向：微分方程数值解法.

詹涌强，杨小辉，谭志明.二维抛物型方程的高精度分支稳定隐格式[J].安徽师范大学学报：自然科学版，2015，38(3)：232-237.

O

A

1001-2443(2015)03-0233-06