客车动力总成惯性参数的辨识

曾发林，葛平莹

(1．江苏大学 汽车工程研究院，江苏 镇江212013;2．江苏大学 汽车与交通工程学院，江苏 镇江212013)

0 引言

随着汽车工业的发展与技术的不断提高，在国内的汽车行业中NVH 特性研究已经受到了足够的重视，作为汽车主要的振源之一的动力总成的振动，其性能的优劣直接影响着整车的NVH 水平［1］．同时，其惯性参数是实现悬置系统设计与优化、动态仿真模拟及有限元分析计算等必不可少的参数，也是评价和确定产品结构性能的必要参数［2］．

目前，国内在汽车行业中采用质量线法来获取动力总成惯性参数［3］的研究尽管越来越多，然而大部分研究仅是针对一些小型汽车，其结构简单、材料性能要求低、质量较轻．而针对大型客车或者货车动力总成的研究相对较少，它们的结构复杂性、材料的性能要求及其本身重量远远超出小型汽车，这种方法是否仍然适用需要进一步的研究．因此，本文的研究对象是某客车六点悬置动力总成系统，在结构上不仅包含了传统意思上的发动机和变速箱，而且还增加了客车动力总成专用的缓速器及附件，其重量也远远超出小型汽车，并且悬吊装置采用的是柔软的弹性绳，使试验结果更加准确．因此，笔者旨在验证对于更加复杂的刚体，基于模态试验法来获取其惯性参数的可靠性．

首先，给出了基于模态试验方法获取刚体惯性参数的原理;其次，将该方法运用于该客车动力总成惯性参数的获取;最后，在已知各组成部分惯性参数的基础上，通过计算整合得到动力总成的惯性参数，并将计算结果与试验结果进行对比分析，验证了该方法对获取复杂刚体惯性参数的准确性和快捷性．

1 基于模态试验法测量惯性参数的原理

1．1 试验理论依据

因为刚体特性参数与基于模态试验的频响函数(FRF)中的质量线之间存在着一定内在关系，从而使用一系列的运动和动态方程组表示这些质量线，确定刚体的惯性属性(质心、转动惯量和惯性积等)．由于被测物体一般不是纯刚体，会出现弹性模态，因此实际的振动加速度频率响应函数曲线如图1 所示．

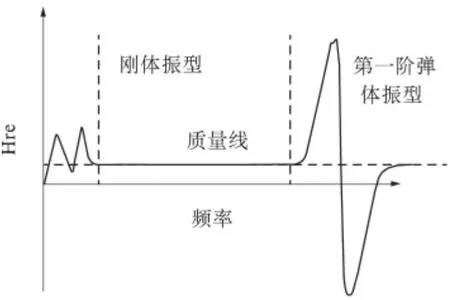
图1 刚体与弹性系统频率响应函数Fig．1 The frequency response functions of rigid body

图中FRF 曲线分为三部分:低频段曲线显示结构在悬吊支撑约束条件下发生一定变形时的柔性模态;中间近似平直线的频段就是质量线，该频段内FRF 值只与质量矩阵［M］中各惯性参数有关，而其是结构的固有属性，不会发生变化;高频段曲线反映的是因被测物体发生弹性变形而引起的弹性体模态［4］．

1．2 计算参考加速度矩阵和力矩阵

对选定频带内所有谱线，对所有响应测量点P，Q，…，对所有被考虑的输入1，2，…，有如下的加速度矩阵形式的运动学关系:

式中:XP，YP，ZP为测点P 在总坐标系中的坐标(或对于给定的参考坐标)．

对应于每一谱线建立的超定方程组(输入自由度数大于或等于6)以最小二乘法求解．

对于所有的输入1，2，…，可得到力矩阵形式的运动学关系:

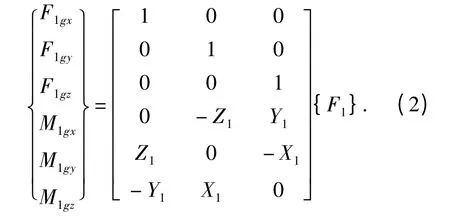
式中:{F1}为输入1 的作用力，N;X1，Y1，Z1为输入1 作用点的总坐标分量．

1．3 计算质心坐标，转动惯量及惯性积

对于每一输入每一谱线、每一输入全体被考虑的频带可列出方程组:

式中:Xcog，Ycog，Zcog为质心在总坐标上的坐标分量;Ixx，Iyy，Izz为刚体对总坐标各坐标轴的轴转动惯量;Ixy，Iyz，Ixz为刚体在总坐标系中的惯性积．

对应每一谱线这些超定方程组(输入数多于或等于2)可采用最小二乘法求解．

2 客车动力总成模态试验

2．1 试验测试系统

本次试验所用仪器如表1 所示．试验所用仪器均是满足国际标准的测试仪器，且全部经过标定，测量范围和精度完全满足试验模态的要求．采用锤击法进行试验［5］．

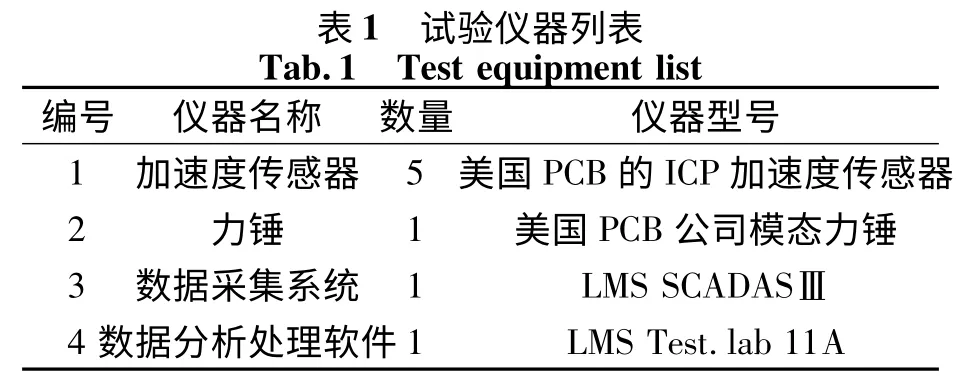
表1 试验仪器列表Tab．1 Test equipment list编号 仪器名称 数量 仪器型号1 加速度传感器 5 美国PCB 的ICP 加速度传感器2 力锤 1 美国PCB 公司模态力锤3 数据采集系统 1 LMS SCADASⅢ4 数据分析处理软件1 LMS Test．lab 11A

2．2 模态试验方法

由于锤击法是一种宽频带激励，需要的设备简单、灵活性大、适合现场操作，所以，本次试验选用锤击法［6］．实验对象为某公司大型客车动力总成，总重量为1 261 kg．

使用柔软的悬挂装置悬吊动力总成，使被测对象处于自由悬挂状态，避免柔性吊绳对动力总成造成约束，允许动力总成在所有的方向运动(平动和转动)，使试验结果更加准确． 悬挂装置一共四个悬吊点，其中两个悬吊点在缓速器两侧，另两个悬吊点在发动机支撑架的两侧，如图2 所示．其中动力总成左侧部分为发动机，中间部分为变速箱，右侧部分为客车动力总成专用的缓速器．

图2 悬吊点位置Fig．2 Suspension points arrangement

建立动力总成的坐标系，以发动机后端面左下方为原点，+x 方向指向汽车正前方，+z 方向垂直向上，根据右手定则确定+y 方向．

2．3 试验设置

为取得较好的数据计算结果，一般要保证所选质量线频段内的频率谱线数大于5 条． 但若在较大的频率范围内，结构本身的质量线数据可以保持相对的恒定值，那么可将采样频率分辨率设置较低，以提高运算速度、加快试验进程．因此本实验设置参数见表2 所示．

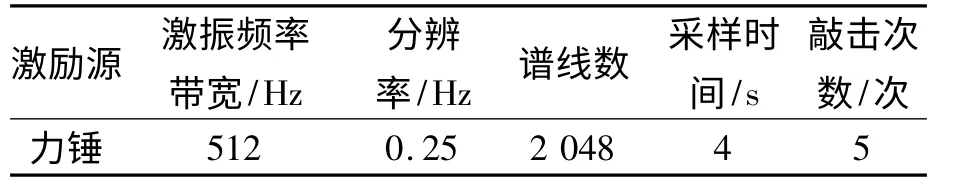
表2 激励参数的设置Tab．2 Excitation parameter settings

力锤激励信号是一个脉冲信号，持续时间短，衰减较快，且在实验过程中可实时查看激励力信号的状况，所以激励信号加力窗函数．而响应信号是结构在冲击后获得一定加速度的自由振动，开始信号阶跃然后逐渐衰减，所以该试验对响应信号加指数窗进行衰减处理［7］．

2．4 模态试验要注意的问题

由于试验结果对加速度与激励力很敏感，所以在实验前应对所有加速度传感器进行标定，以保证数据的准确性并提前排除有故障的传感器和数据传输线．用质量线法计算惯性参数时，参与计算的数据是低频范围内的FRF 值，所以应选用较软的锤头，本实验选用塑料锤头的力锤进行激励脉冲输入．

激励点和响应点的选择遵循的原则［8］:激励点和响应点都应在局部刚度较大的位置选取，以防止局部弹性变形影响测试结果;应尽量多地选取激励点和响应点，本次试验选取25 个激励点，共52 个单向响应点;激振点位置的选择应避开支撑点和结构模态振型节点，响应点的选择主要考虑其能反映结构的主要轮廓;激励点和响应点不应布置在同一平面内，更不宜分布在同一条直线上［9］．本实验针对动力总成实际结构，选择了相应的激励点和响应点，部分如图3 所示．

图3 部分响应点和激励点位置Fig．3 Partial response and excitation point

2．5 数据处理及计算结果

在LMS 的modal data selection 中选取合理的频率响应函数(FRF)曲线，采用刚体特性计算模块(Modal Rigid Body)，在Mass 栏输入动力总成质量m=1 261 kg，在Node name 栏中输入质心名称进行计算． 在保证LMS 软件允许计算的情况下，注意以下几点:保留尽量多的激励点和响应点;选取关心频率带内较为平滑的FRF 曲线数据;选取尽可能宽的FRF 频带，如图4 所示．

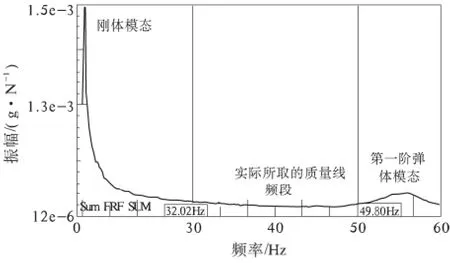
图4 动力总成的频响函数Fig．4 The FRF curve of the powertrain

动力总成惯性参数试验计算结果如下:

质心坐标x=0．874 7 m，y= -0．060 6 m，z=0．241 2 m．转动惯量Ixx= 51．399 kg·m2，Iyy=411．426 kg·m2，Izz= 373．822 kg·m2．惯性积Ixy= - 6．235 kg·m2，Ixz= - 2．918 kg·m2，Iyz= - 20．051 kg·m2．

3 动力总成惯性参数的计算整合

首先，通过企业所给数据知道了发动机、变速器和缓速器的各自质量以及在各自坐标系下质心位置，其中发动机质量为840 kg，变速箱质量为335 kg，缓速器质量为85 kg． 笔者在发动机上建立的参考坐标系与动力总成的参考坐标系重合，所以要把变速器和缓速器的质心坐标转换到发动机或者动力总成参考坐标系中，再由物体质心坐标一般公式求得动力总成系统的质心位置，已知数据和计算结果如表3 所示［10］．

表3 在动力总成参考坐标系下的质心坐标Tab．3 The centroid coordinate in the powertrain coordinates

其次，在已知各部分绕各自质心位置的转动惯量和惯性积后，如表4 所示，再由转动惯量和惯性积的平行轴方程式，得到各部分绕动力总成系统质心位置的转动惯量和惯性积，进而通过叠加可以得到动力总成绕质心位置的转动惯量和惯性积，并与模态试验法所得结果进行了对比，计算结果如表5 所示．

转动惯量和惯性积的平行轴方程式如下所示:

式中:(Ix＇x＇)G，(Iy＇y＇)G，(Iz＇z＇)G分别表示动力总成各个 部 分 绕x，y，z 轴 转 动 惯 量 的 和;(Ix＇y＇)G，(Ix＇z＇)G，(Iy＇z＇)G表示 动 力总 成各 个部 分惯 性 积 的和;xG，yG，zG表示动力总成质心坐标与总成某一部分质心坐标的距离．

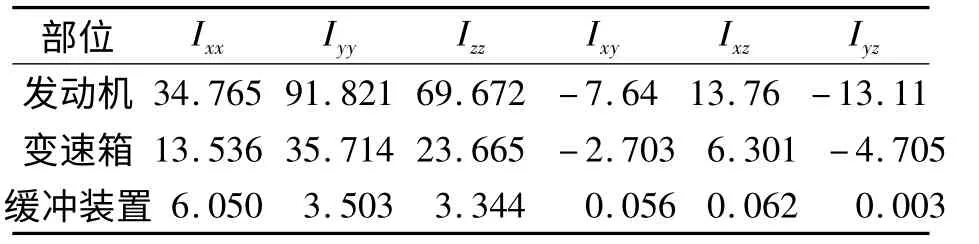
表4 动力总成各部分的转动惯量和惯性积Tab．4 Moment of inertia and product of inertia of each part in power assembly kg·m2

表5 动力总成的转动惯量和惯性积Tab．5 Moment of inertia and product of inertia kg·m2

对比两种方法可知，计算结果具有较好的一致性，在3 个方向上的惯性参数的误差值均在10%以内，符合工程上的要求，显示了通过质量线法获取结构更加复杂的客车动力总成惯性参数的测试精度比较高［11］．

产生误差的原因可能是:当动力总成进行模态试验时，其响应信号中不可避免地会混入一些干扰噪声，从而使真实值与测量值之间产生一定的误差;由于动力总成材料、结构复杂，在悬吊过程中平衡点比较难找，有时会卸下一些质量很轻的铁片，这也会对试验差生较小的误差．

4 结论

介绍并应用了一种获取复杂刚体惯性参数的有效方法，即基于模态试验的刚体惯性参数识别法(质量线法)．文中首先给出了质量线法的理论依据，采用基于模态试验的方法获取了客车动力总成的惯性参数，同时将试验结果与计算整合得到的结果进行对比分析，对比结果显示了该方法对获取复杂刚体的惯性参数具有较高的测试精度．由于该方法操作方便，需要的设备简单，总体可操作性强，加之其精确的测试结果，以后在复杂刚体惯性参数的测试中必然会有更广泛的应用．除此之外，文中最后也对引起试验误差的可能性进行了分析．

［1］ 赵夕长，时培成． 动力总成悬置系统振动分析与解耦优化［J］． 农业装备与车辆工程，2010(5):7 -10 ．

［2］ 龙岩．动力总成惯性参数识别的试验研究［J］．噪声与振动控制，2009，22(1):73 -76 ．

［3］ 俞斌，庄德军，明新国．汽车动力总成惯性参数的辨识［J］．传动技术，2008，22(1):38 -45．

［4］ 何岩松，荣申强，徐中明，等．基于频响函数的结构惯性参数识别与应用［J］．世界科技研究与展，2010(4)，488 -490．

［5］ 王佳，潘宏侠，杨晓波．基于PolyMAX 法的齿轮箱试验模态分析［J］．机械传动，2013，37(2):66 -75 ．

［6］ 刘军，高建立，穆桂脂等．改进锤击法试验模态分析技术的研究［J］．振动与冲击，2009(3):174 -177．

［7］ 张力． 模态分析与实验［M］． 北京:清华大学出版社，2011．

［8］ 任永连，周竑，束元．基于质量线法的汽车动力总成惯性参数的研究与辨识［J］． 汽车技术，2013(7):25 -30．

［9］ LEE H，LEE Y B，PARK Y S．Response and excitation points selection for accurate rigid-body inertia properties identification［J］． Mechanical Systems and Signal Processing，2004，13(4):571 -592．

［10］岳光杰．车辆动力总成悬置系统振动分析及优化设计［D］． 重庆:重庆交通大学机电与汽车工程学院，2013．

［11］陈海朝，周文超．基于模态试验法测量整备驾驶室质心和转动惯量［R］． 上海:第一汽车股份有限公司，2012．