长大上坡沥青路面抗剪强度设计方法研究

吕彭民，桂发君，张 扬

(1．长安大学 道路施工技术与装备教育部重点实验室，陕西 西安710064;2．西安陕鼓动力股份有限公司，陕西 西安710075)

0 引言

研究表明，车辙是最常见的沥青路面病害形式之一［1］．长大上坡路面在低速、重载等条件下，车辙病害更加严重，特别是温度较高的夏季，车辙形成速度快，严重影响行车安全［2］． 目前，国内外学者均没有将长大上坡路面的受力特点作为路面结构设计的参考因素，使得现有的长大上坡沥青路面过早的出现了车辙病害． 我国沥青路面的车辙大部分是流动型车辙，这是因为抗剪能力不足，沥青混合料在剪切力的作用下产生流动变形而形成的［3］．研究发现，在实际交通荷载下，沥青路面因受到纵向剪应力(或剪应变)而产生的变形能够得到一定程度的强制恢复，而受到横向剪应力(或剪应变)产生的变形由于累积效应，路面破坏严重且不能恢复［4］;同时，通过计算分析发现，长大上坡沥青路面面层内部的横向剪应变明显大于纵向剪应变．为此，笔者针对移动荷载作用下的长大上坡路面动力学模型进行研究．

1 剪切流动变形及影响因素的分析

长大上坡沥青路面受力存在如下特点:①在相同荷载条件下，路面受到的剪应力与坡度大小正相关;②沥青混合料模量、抗剪强度等与温度负相关，且温度较高时会显著下降，使得路面易产生流动变形;③重载车辆上坡时，通常降档减速，相当于延长了荷载作用时间，根据时温等效原理［5］，等同于提高了路面温度，加剧了长大上坡路面的剪切流动．根据上述分析可以看出，载重、速度、坡度和温度是长大上坡沥青路面产生流动变形的最关键因素．

2 剪切应力模型的建立

2．1 有限元模型的建立

2．1．1 移动荷载的实现

笔者选择项目中某高速公路半刚性基层沥青路面结构进行研究，采用Abaqus 软件，利用Fortran 语言编写了Dload 及Utracload 的子程序，用来分别模拟长大上坡路面实际交通荷载下的车辆各轮对路面的垂直和水平移动荷载的作用，根据车辆的行驶距离和预先设定的载荷步时间来确定垂直和水平移动荷载作用的速度．

根据本项目组对现有几条高速公路车辆组成的调查发现［5］:目前国内高速公路上的载重车主要是二轴车，尤其是1 +2 型二轴车，其次为三轴车和四轴车中的1 +5 型、1 +1 +5 型及1 +2 +5型车辆居多，这里选择具有代表性的1 +2 型二轴车和1 +1 +5 型四轴车进行研究．

考虑到实际路面情况，由于沿行车方向路面结构、移动荷载均对称分布，因此，只需研究车辆轮载作用区域的一半，即取整体路面宽度的一半(即单侧1/2)进行建模，1 +2 型二轴车作用下单侧各轮对沥青路面的移动荷载的模拟图见图1．笔者选取矩形均布压力模式来模拟各轮的作用力，同时认为轮胎的接地压力与标准胎压(取0．7 MPa)相等．此外，上坡路段行驶车辆各轮施加给路面的水平力由本项目组根据现场试验结果建立的水平力计算模型算得［5］．

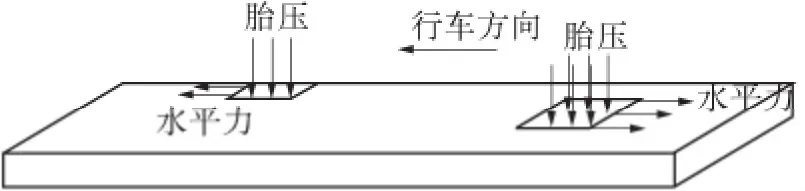
图1 1 +2 型二轴车荷载作用下移动荷载的模拟(单侧1/2)Fig．1 Simulation of moving load by the 1+2 two-axis vehicle (one side 1/2)

2．1．2 边界条件及网格划分

根据圣维南原理和参考文献［6］，路面结构模型的几何尺寸取为:10 m(沿行车方向，即纵向)×4 m(路面厚度，即垂向)×3 m(路面宽度，即横向)． 边界条件为:模型的底部(y = -4 m处)，U2 =UR1 =UR3 =0;模型的前后(z = ±5 m处)，U3 = UR1 = UR2 =0;模型右边界(x =3 m处)，U1 =UR2 =UR3 =0;模型的左边界(x =0 m处)，设成沿x 方向的对称边界约束条件． 采用三维实体单元C3D8R 建立路面模型，划分网格情况见图2．1 +1 +5 型四轴车的建模方法之与相同．

图2 沥青路面有限元模型及网格划分(1/2)Fig．2 Finite element model for asphalt pavement and meshing(1/2)

2．1．3 沥青路面结构动力学有限元方程

当沥青路面所受荷载时间很短或受到动态荷载时，需要采用动态分析方法进行动力学研究，从而获得沥青路面的动态响应［7］．

根据Hamilton 变分原理及相关力学知识，建立了如下系统动力学有限元方程:

［M］{δ¨}+［C］{δ·}+［K］{δ}={F(t)}． (1)

式中:［M］为系统的总质量矩阵;{δ}、{δ·}、{δ¨}为系统中离散点的位移、速度和加速度的向量表达形式;［K］为系统的总刚度矩阵;［C］为系统的总阻尼矩阵;{F(t)}为路面动力系统的荷载矩阵．

［C］=α［M］+β［K］． (2)

式中:α，β 为比例常数，与沥青路面结构的固有频率和阻尼比有关．

这里采用Abaqus 软件中的动力学分析模块对方程(1)进行求解，从而获得沥青路面在各种参数下的动力学响应．

2．1．4 路面结构及材料参数

试验路段沥青路面的结构形式和材料参数见表1．由于半刚性沥青路面的基层和底基层选用水泥稳定材料，温度对其性能影响较小［8］，所以不考虑温度对基层和底基层的影响．

根据BELLS 修正模型［9］能算出不同温度下的沥青层模量，见公式(3)． 根据《公路沥青路面设计规范》选取20 ℃时的各沥青层模量值．

ET=E20×100．018(20-T)． (3)

式中:E20为沥青混合料在20 ℃时的模量，MPa;T为沥青混合料温度，℃;ET为沥青混合料在T 下的模量，MPa．

表1 路面结构及材料参数Tab．1 Pavement structure and material parameters

2．2 计算工况设计

为了研究长大上坡路段载重、速度、坡度和温度等因素与面层内部最大横向剪应变之间的关系，参照正交试验方法，在标准胎压(取0．7 MPa)及标准荷载下，对坡顶位置(最易形成车辙的位置)进行各变量的交叉组合计算，正交计算工况如表2 所示．

表2 正交计算工况Tab．2 Orthogonal calculation case

由于计算量大，笔者只对标准载荷情况下各交叉组合工况进行有限元计算．首先，建立表2 中各变量与面内横向剪应变的关系式;然后，考虑到载重的影响，建立包括载重和表2 中各变量在内的面内最大横向剪应变模型．

2．3 计算结果

选取1 +2 型二轴车，在标准荷载情况下进行试验，得到不同入坡速度、坡度和温度时各组合工况下的面内最大横向剪应变的有限元计算结果分布见图3．1 +1 +5 型四轴车类似．

由图3 可知:面层内部最大横向剪应变随着入坡速度v0的减小、坡度α 的增加和温度T 的升高而增大;其中温度的影响最为显著．

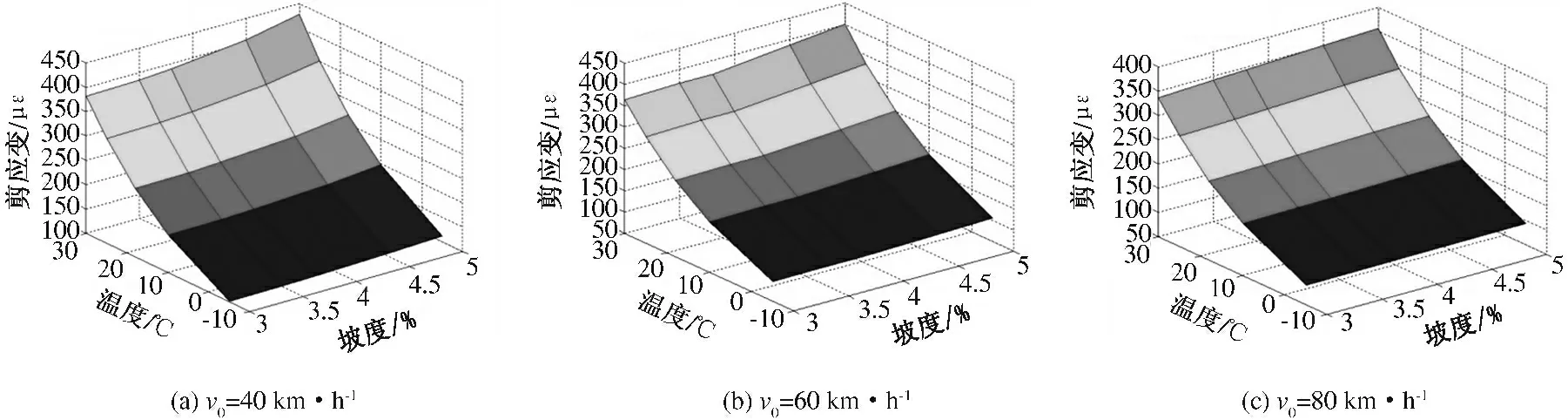
图3 1 +2 型二轴车标准荷载下不同入坡速度时面层内部最大横向剪应变分布图Fig．3 Distribution of maximum transverse shear strain in the surface layer of 1 +2 two－axis vehicle with standard load by different speed into the slope

2．4 剪切应力模型的建立

2．4．1 拟合函数形式的选择

为确定面内最大横向剪应变ε0与速度v、坡度α 和温度T 等变量之间的函数关系，笔者分别选取线性函数、对数函数、多项式函数、幂函数、指数函数等5 种函数形式进行拟合，通过相关性对比分析发现，相关性最高的函数形式为指数函数，故取面内最大横向剪应变与各变量之间的拟合函数表达式为

ε0=a0e(a1v+a2α+a3T)． (4)

式中:ε0为面内最大横向剪切应变，με;v 为坡顶速度，km/h;α 为坡度，%;T 为温度，℃;a0，a1，a2，a3为待定的回归系数．

2．4．2 函数拟合

采用SPSS 统计软件，按照公式(4)的函数形式将图3 中的数据结果进行多元非线性回归，即可确定1 +2 型二轴车和1 +1 +5 型四轴车标准荷载下，面内最大横向剪应变与速度、坡度及温度的拟合函数表达式:

1 +2 型车辆作用下:

1 +1 +5 型车辆作用下:

ε0=154．238e(-0．0036v+0．0001α+0．0382T)，R2=0．990． (6)

以上函数表达式均是在标准载荷情况下分析得到的，并没有考虑到载荷变化的影响．图4 给出了二轴车和四轴车分别在入坡速度为60 km/h、坡度为3．8%、温度为30 ℃时，不同荷载情况下的面内最大横向剪应变的分布关系．由图4 可知，面内最大横向剪应变与车辆荷载质量线性相关，拟合表达式如下．

1 +2 型二轴车作用下:

εW=0．018 8W+286．21，R2=0．937． (7)

1 +1 +5 型四轴车作用下:

εW=0．003 9W+370．26，R2=0．923． (8)

式中:W 为车辆的实际荷载质量，kg．

由式(7)和式(8)的线性关系，可得图5 所示任意载荷与面层内部最大横向剪应变的曲线(其中，W0为标准载荷时的荷载质量，ε0为标准载荷作用下的最大横向剪应变)．

由图5 可知，利用曲线斜率k 和任意一点的坐标，就能表达出任意载荷下的面层内部最大横向剪应变的大小，见式(9):

ε=ε0+Δε=ε0+k(W-W0)． (9)

将式(4)代入式(9):

ε=a0e(a1v+a2α+a3T)+k(W-W0)． (10)

式中:ε 为各因素影响下的面内最大横向剪应变，με;k 为曲线斜率．

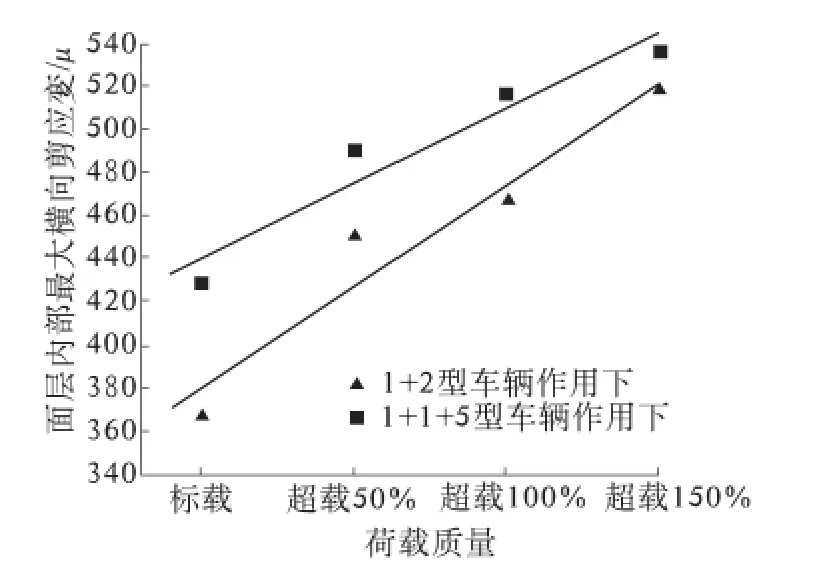
图4 不同荷载质量对面内最大横向剪应变大小的影响Fig．4 Influence of different qualities and the maximum transverse shear strain in the surface layer

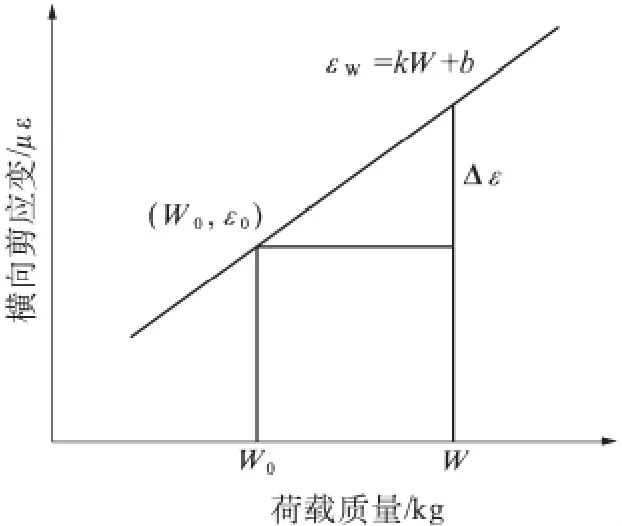
图5 面内最大横向剪应变与荷载质量关系曲线图Fig．5 Graph of the maximum transverse shear strain in the surface layer and quality

由虎克定律可知，面内最大横向剪应力τ 的函数关系式为

τ=G·ε·10-6． (11)

式中:G 为剪切模量，MPa．

因此，式(10)也可转变为剪应力模型:

τ=G·(a0ea1v+a2α+a3T)+k(W-W0))·10-6．(12)

结合式(5)～(8)及式(12)即可得到1 +2 型二轴车和1 +1 +5 型四轴车载荷作用下，包括载重W、速度v、坡度α 和温度T 等变量在内的面层内部最大横向剪应力τ 的拟合函数形式，见式(13)和式(14):

1 +2 型车辆荷载作用下:

τ=G·(0．018 8(W-500 0)+148．171·

e-0．0044v+0．0029α+0．038T)·10-6． (13)

1 +1 +5 型车辆荷载作用下:

τ=G·(0．003 9(W-178 00)+154．238·

e(-0．0036v+0．0001α+0．0382T))·10-6． (14)

公式(12)即为包括载重、速度、坡度和温度等变量在内的长大上坡沥青路面面层内部最大横向剪应力模型．该模型可为多因素作用下长大上坡沥青路面面层内部最大横向剪应力的分布、车辙产生原因及长大上坡沥青路面的结构设计等研究提供理论支撑．

3 长大上坡沥青路面控制指标研究

综合以上分析，我国半刚性基层沥青路面容易产生流动型车辙变形的关键力学原因是:面层内部受到的横向剪应力(或剪应变)超过了允许范围，然而现有的沥青路面在结构设计和实际施工中均未考虑剪应力(或剪应变)的影响，而且目前在长大上坡沥青路面的设计和实际施工中，还没有提出可供参考的相关控制指标的执行标准及设计方法． 针对以上问题，建议在路面结构设计中，增加考虑面层内部抗剪性能的控制指标，即面内最大横向剪应力τ．同时，在沥青路面的实际施工中，增加抗剪强度τ0作为控制指标．

(1)根据面内剪应力的大小进行控制:

τ≤［τ］=τ0/n． (15)

式中:τ 为面内最大横向剪切应力，MPa;［τ］为设计时面内允许最大横向剪切应力，MPa;n 为安全系数;τ0为面层材料的抗剪强度，MPa．

此方法要求在路面结构设计中，必须控制面内最大横向剪应力τ，使其小于或等于允许的最大横向剪应力［τ］．

(2)根据沥青混合料的抗剪强度和路面施工质量控制，式(15)可变为

τ0≥nτ． (16)

此方法要求在控制混合料级配或检验路面施工质量时，务必控制面层混合材料的抗剪强度τ0，使其大于或等于设计时的最大横向剪应力τ与安全系数n 的乘积．因此，分别将τ 作为沥青路面结构设计时的控制指标，τ0作为检测施工质量的控制指标，两者统一且相互制约，可弥补现有规范的不足．

4 长大上坡沥青路面综合车辙预测模型

文献［3］给出了沥青层厚度、沥青路面的温度、轮载作用次数、路面最大剪应力和混合料的抗剪强度等变量在内的车辙深度的关系式:

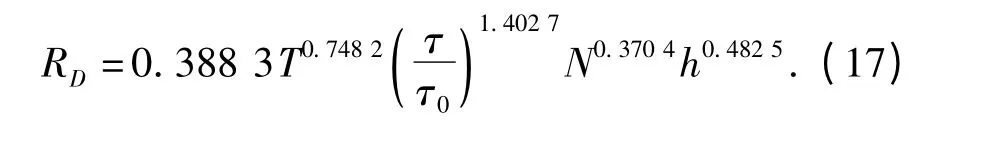
式中:RD为沥青路面车辙深度，mm;T 为沥青路面温度，℃;τ 为在车辆荷载作用下的沥青路面最大剪应力，MPa;τ0为路面材料的抗剪强度，MPa;N 为轮载作用次数;h 为沥青路面沥青层厚度，cm．

将式(12)代入式(17)，可得

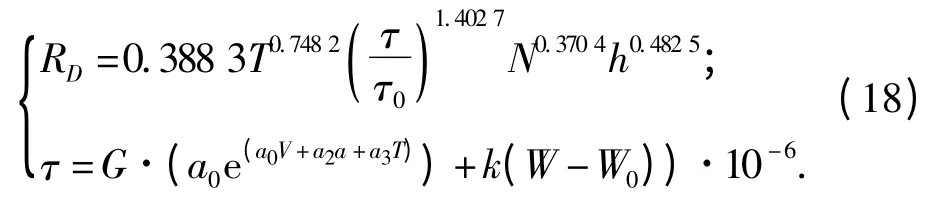
对于1 +2 型二轴车和1 +1 +5 型四轴车车辆荷载作用下，τ 的大小根据式(13)和式(14)算得．公式(18)即为包括载重、速度、坡度和温度等影响因素在内的坡道沥青路面车辙综合预估模型，该预估模型为长大上坡沥青路面的车辙预测提供了一种计算方法．

5 结论

(1)由长大上坡沥青路面的受力特点可知:载重、速度、坡度和温度是长大上坡沥青路面产生流动型车辙变形的最关键因素;

(2)建立了包括载重、速度、坡度和温度等影响因素在内的长大上坡沥青路面面层内部最大横向剪应力计算模型，以及沥青路面车辙综合预估模型;

(3)建议将面层内部最大横向剪应力τ 增加为长大上坡沥青路面结构设计的控制指标，将面层材料的抗剪强度τ0增加为路面实际施工质量的控制指标．

［1］ 崔文博，郝培文． 基于Ham-burg 车辙试验的沥青路面车辙损坏分析［J］． 中外公路，2014 ，34(1):95-98．

［2］ 吴浩，裴建中，张久鹏． 长大纵坡路段沥青路面车辙规律及影响因素［J］． 长安大学学报(自然科学版)，2009，29(6):28 -31．

［3］ 鲁正兰，孙立军． 沥青路面车辙预估方法的研究［J］． 同济大学学报(自然科学版)，2007，35(11):1476 -1480．

［4］ 闫卫红，孟枫林，董忠红． 移动荷载下半刚性基层沥青路面剪应变研究［J］． 郑州大学学报(工学版)，2010，31(2):47 -51．

［5］ 许丽明． 长大上坡路段车辆对路面动作用力的研究［D］． 西安:长安大学公路学院，2012．

［6］ LU Pengmin，TIAN Runli，LIU Xiaoyun． Dynamic response solution in transient state of viscoelastic road under moving load and its application［J］． Journal of Engineering Mechanics，2010，136(2):168 -173．

［7］ PEI Jianzhong，WU Hao，CHEN Yong，et al． Dynamic response characteristics of asphalt pavement under multi-axle moving load［J］． China Journal of Highway and Transport，2011，24(5):26 -31．

［8］ 武建民，马君毅，戴经梁． 温度对水泥稳定旧沥青路面材料强度的影响［J］． 武汉理工大学学报(交通科学与工程版)，2009，33(17):54 -56．

［9］ 谈至明，吁新华． 沥青面层的截面弯曲刚度当量模量计算［J］． 中国公路学报，2012，25(6):37 -42．