高精度磁浮式定位平台控制问题研究

张和洪，龙志强

(国防科技大学 机电工程与自动化学院,长沙 410073)

高精度磁浮式定位平台控制问题研究

张和洪，龙志强*

(国防科技大学 机电工程与自动化学院,长沙 410073)

高精度定位平台是光刻机、纳米测量与加工、微装配等微观领域技术的核心部件。磁浮式定位平台由于运动平台和驱动机构采用非接触式的磁浮技术，消除了两者间的摩擦、磨损等对运动精度造成的影响，提高了定位精度，成为近年来国内外精密定位技术研究的热点。简述国内外磁浮式定位平台的发展与研究现状，提出一种三点悬浮式的单运动部式的磁浮式定位平台，建立其悬浮方向上的单电磁铁模型，考虑到模型复杂性与不确定性、间隙干扰、负载扰动等原因对定位平台稳定悬浮控制问题的影响，引入自抗扰控制技术并且进行数值仿真与实现。结果表明，对悬浮方向上的控制问题引入自抗扰控制技术，不仅能实现稳定悬浮控制而且系统具有很强的鲁棒抗干扰能力。

磁悬浮；定位平台；自抗扰控制

0 引 言

随着现代科学技术的快速发展，微电子技术、微机电系统技术、微加工微制造技术、纳米技术等微观领域的研究越来越深入。微定位技术作为微观领域研究的关键技术之一，其技术发展水平直接影响到微观领域的发展水平，这使得微定位技术的研究具有极为重要的现实意义[1-2]。微定位技术中的精密定位平台广泛应用在半导体光刻加工、超精密测量、生物芯片等现代精密、超精密加工领域。根据精密定位平台的应用领域和工作性质的不同，其需要具备不同数量的运动自由度使工件获得高精度的定位位置和姿态。随着运动自由度数量的增加，精密定位平台的结构将更加复杂，其定位精度、运动速度、运动加速度等性能参数将下降，若要获得较高的性能参数，其制造成本将急剧增加。磁浮式定位平台由于运动平台和驱动机构采用非接触式的磁悬浮驱动技术，消除了摩擦、磨损对运动精度造成的影响。传统的接触式的定位平台主要问题是高精度与大行程之间的矛盾。为解决这一矛盾，采用了粗动微动两端式定位方式，但是即便采用定位精度较高的直线电机驱动粗动台的方式依然受到接触式导轨所产生摩擦等因素的限制，其定位精度仍然有待提高。磁浮式定位平台依靠磁悬浮力进行支撑，支撑刚度较高且运动平台与驱动机构之间无机械接触，理论上，磁浮式定位平台可以达到很高的激励响应和定位精度，实现大范围高精度的微运动，获得一种应用于各领域且成本相对较低的精密定位平台，因此磁浮式定位平台成为近年来国内外微定位技术研究的热点[3-4]。

磁悬浮技术发源于德国，目前国内外在磁悬浮方面的研究工作主要集中在磁悬浮列车方面，进展相当快，已经从实验研究阶段向试验运行、商业化运行阶段转变[5-7]。磁悬浮列车依靠电磁力实现了列车与轨道的分离，以直线电机作为牵引动力，具有噪声低、振动小，无尾气污染，爬坡能力强等优势而受到业内外人士的关注与支持。当前在悬浮导向系统、牵引系统、供电系统、列车控制与诊断系统等方面已取得相对成熟的技术成果[8-9]。除此之外，磁悬浮技术还应用于磁悬浮轴承、高速磁悬浮电机、风洞磁悬浮系统、磁悬浮隔振系统以及磁悬浮熔炼等方面。

文中简述了磁浮式定位平台的国内外发展与研究现状，提出了三点悬浮式的磁悬浮式定位平台的机构方案。针对悬浮力与推动力相互解耦的磁浮式定位平台的悬浮方向上的控制问题展开研究，通过建立磁浮式定位平台悬浮方向上的单电磁铁模型，引入自抗扰控制技术，从而实现悬浮方向的稳定悬浮控制。

1 磁浮式定位平台的发展与研究现状

目前磁浮式定位平台的结构形式主要有导轨叠加式和单运动部式。导轨叠加式是在传统定位平台的导轨上采用磁悬浮技术，以消除摩擦力，提高导轨的运动控制性能。但它的定位平台结构复杂，受机械制造装配精度的影响，成本较高，且难以实现多自由度运动。单运动部式定位平台是指依靠一个动子相对于定子的运动实现多自由度的定位。利用磁悬浮技术使动子悬浮于定子，在提供平衡动子重力的支撑力的同时，可以驱动动子在沿z轴和绕x、y轴方向上运动和定位。单运动部式磁浮式定位平台为了实现磁悬浮，有两种方式：①悬浮力和推力由同一部件提供，该结构未能完全实现悬浮力和推力间的解耦，平台的构造简单但控制较为复杂；②悬浮力和推力由不同部件分别完成，这种结构实现了悬浮力和推力间的解耦，平台的结构复杂但控制较为简单。

1.1 磁浮式定位平台国内外发展现状

磁浮式定位平台的自身结构特点和电磁执行单元的电气参数设计共同决定了磁浮式定位平台的静态、动态力学特性。为了满足精密加工等行业对定位精度的技术要求，设计出一种新颖、紧凑和高精度的定位平台是研究的方向。以下主要从整个系统平台的角度出发，简述国内外具有代表性的磁浮式定位平台的发展现状。

1.1.1 国外发展现状

1995年，Won-Jong Kim等人设计并制造了世界上第一个由4台直线电机驱动的磁悬浮定位平台原型机[10]。设计该平台的目的是用于半导体制造中的光刻技术，完成对晶片的精密定位。定位平台原型机最大行程可达到50 mm×50 mm，定位精度可达5 nm，平面驱动加速度>1 g(10 m/s2)。这种定位平台通过对其下部永磁平面电机的控制，可实现6自由度精密运动。

2004年，Shobhit Verma等设计了一种精密磁浮6轴纳米定位平台[11]。平台主要应用于纳米尺度上的微装配与微制造。这种定位平台的定位分辨率达到5 nm。工作台的移动速度为0.5 m/s，加速度为30 m/s2，每个水平驱动器所消耗的能量为15 mW，每个竖直驱动器消耗的能量为320 mW，负载能力为1 kg。在x，y，z方向上的最大行程为300 μm，并且具有3.5 mrad的旋转行程。

2004年，Kim等研制了一种新的精密6自由度集成定位平台[12]。该定位平台的性能参数特别适用于半导体加工制造，定位平台采用激光干涉仪进行位置测量。定位分辨力达到20 nm，x和y方向上的定位误差(position noise)为10 nm/rms，z方向上的定位误差(position noise)为100 nm。平面行程为160 mm×160 mm。y方向最大速度为0.5 m/s，加速度为5 m/s2。这种定位平台使用了集中域(concentrated-field)式的磁矩阵(magnet matrix)作为定子，而线圈则布置在三角形的动子上，这种结构可将6个独立的力联合起来以产生6自由度的运动。

2006年，Kim和Verma又提出了一种Y型磁浮平台,“Y”表示悬浮工作台的形状[13]。这种定位平台行程达到5 mm×5 mm，为三角形定位平台的15倍。由于目前所用传感器所限，z方向的行程可达500 μm，旋转行程可达3.5 mrad。然而，定位平台的机械结构允许转动的范围为87.3 mrad，z方向行程为7 mm。

2010年，Ho Yu和Won-jong Kim提出了对这种定位平台的改进方案，利用霍尔传感器进行位置的测量，使得定位平台的移动不受限制[14]。这种基于霍尔传感器的定位平台的行程为220 mm×220 mm。

1.1.2 国内发展现状

浙江理工大学的陈本永从2005年开始研究磁浮定位平台，并于2006年提出了两种方案[16]。其中，4组永磁阵列分别嵌入在运动平台底面的4边中间,与之对应布置4组定子绕组,运动平台在永磁阵列和定子绕组间电磁力的相互作用下被浮起和产生运动,通过控制通入4 组定子绕组电流的大小和方向,可实现运动平台x、y、z、θx、θy、θz共6个自由度的微运动。4 组衔铁分别嵌入在运动平台上面的4角,与之对应布置4 组电磁铁,通过控制电磁铁电流大小对z方向浮力进行补偿。目前这种定位平台实验装置只能达到微米级精度。

西安交通大学的郑学强等人设计了一种新型磁悬浮定位平台[17]。其结构与浙江理工的陈本永所设计的定位平台有相似之处，不同之处在于永磁阵列作为定子布置。平台下部安装有电磁线圈，水平驱动力的控制为直流电源，简化系统控制的难度，其效果类似于直流驱动直线电机。目前还处于概念设计，仿真实验阶段。

此外哈尔滨工业大学、东南大学、清华大学等对磁浮式定位平台都有一定的研究[18-21]。总之，国内学者对磁浮式高精度定位平台的研究不多，不够深入。大部分仅限于理论设计分析计算仿真，能够进入实验阶段很少。而且相比国外的试验样机，能够达到的精度仅为微米级。

1.2 磁浮式定位平台国内外研究现状

磁浮式定位平台是一个复杂的综合性系统，其机械结构设计、测量机构设计、控制器设计、驱动器设计等对保证系统高定位精度、高响应速度都具有重要的作用。以下将从测量系统、控制器设计的角度出发，分析目前常见的设计流程与相应的设计方案。

1.2.1 磁浮式定位平台控制器设计

控制器是磁浮式定位平台控制系统的核心，系统性能的好坏取决于控制器单元的性能。目前国内外针对磁浮式定位平台的控制器的设计主要包含4个部分：①建立单个平面电机驱动器的电磁力模型。通过直轴交轴分解法可将绕组电流中用于提供悬浮力和水平推力的分量解耦，并给出交直轴电流与绕组三相电流间的变换关系；②进行平面电机的动力学分析。建立多个驱动器的驱动器力与平面电机模式力之间的折算关系；③根据模式力建立平面电机6自由度的解耦动力学模型；④根据解耦动力学模型分别设计6自由度的位置伺服控制器。

由于微定位领域的定位要求与常规的定位有较大的区别，其面临许多新的问题，比如由于微定位过程的机理的研究不充分使得模型建立的误差较大，在微小的位移范围内明显的非线性现象，系统模型的不确定性，内部参数摄动，在测量环节引入的测量噪声等，使得磁浮式定位平台的控制器设计极具复杂性。W-J Kim采用DQ解耦和局部近似线性化的方法实现了在工作点附近小范围内的控制[10]，J-W Jeon等人提出采用滑模变结构控制代替超前—滞后控制，提高了系统精度和抗干扰能力，但是并没有给出悬浮力与水平驱动力的解耦过程[4]，目前，据统计70%以上的超精密定位平台使用PID调节器、反馈线性化控制以及最优控制策略[3]，采用比例微分超前作用来对消调节对象中的大惯性。

1.2.2 磁浮式定位平台测量系统设计

定位平台的控制器设计需要位置检测系统来实时地反馈位置信号，而位置精度也是通过位置检测系统来反映，因此位置检测精度直接决定了位置控制的精度。对位移传感器的要求是具有高精度和高响应速度，其次还必须具有高的稳定性，抗干扰能力强，抗磁场影响强，线性度好的特点。

目前国内外针对磁浮式定位平台的测量系统中常用的位移传感器有：电容传感器、激光测距传感器和激光干涉仪等。

电容传感器和激光测距仪的测量范围小，不适合于对工作台水平方向上大范围移动进行位置测量，多用于z方向位移的测量。激光干涉测量系统具有较大的测量量程，可满足动子的水平行程要求。其光路的布置灵活，可以针对不同结构形状的动子合理地设计反射镜的安装位置和相应的光路。具有较高的测量速率和纳米级的分辨率。基于这些优点，常用激光干涉测量系统测量工作台水平x和y向上的位移。对于θx、θy和θz这3个自由度上的角度位移也可以附加激光干涉仪或角度传感器测量。其中θx、θy可以利用多个测量z轴位移的电容传感器综合得到。可见目前国内外的6自由度位移测量系统普遍是由激光干涉仪和其他单轴传感器组合而成。

2 磁浮式定位平台悬浮方向上悬浮控制问题

本文旨在设计一种广泛适用于精密工程领域的多自由度磁浮式定位平台。采用单运动部式结构，动子依靠电磁力悬浮于定子，平面电机作为驱动器为动子提供多自由度的定位运动。使之具备应用于

多种精密工程领域的技术潜力，并特别针对芯片制造领域中光刻机的发展趋势对其中定位平台所提出的新要求进行控制方面的研究，最终达到满足应用于极紫外光刻机的性能要求。

为此本文构造了一种新型的三点悬浮式的磁浮式定位平台，该平台的悬浮力和推力由不同部件分别提供，实现悬浮力和推力之间的解耦。由于本文仅针对定位平台的悬浮方向上的控制问题展开研究，故仅给出定位平台悬浮方向上的三点悬浮示意图，见图1。在这种磁浮式定位平台中，利用电磁铁模块提供电磁力，使得定位平台的重力与悬浮力平衡，实现动子在沿z轴、绕x轴、绕y轴方向的3个自由度的运动。而且实现z轴方向上的稳定悬浮是磁浮式定位平台实现其他自由度运动的前提与关键所在，故本部分将针对定位平台的悬浮问题，通过建立相应的单电磁铁模型，引入自抗扰控制策略，使得平台在z轴方向上实现稳定悬浮。

图1 磁浮式定位平台三点悬浮示意图Fig.1 Schematic diagram of scheme of three-point magnetic levitation positioning stage

2.1 磁浮式定位平台单电磁铁模块建模

三组电磁铁模块被固定安装在同一平面上，对应采用三组控制器进行控制，不失一般性，以一组电磁铁模型来进行分析与控制器设计。磁浮式定位平台悬浮方向上的单电磁铁模型主要有U型电磁铁、安装固定板、线圈、运动平台上的衔铁部分等组成，见图2。在电磁铁线圈绕组中通以一定大小的电流会产生电磁力，通过控制其电流的大小，使该点负载的重力与此电磁力平衡。

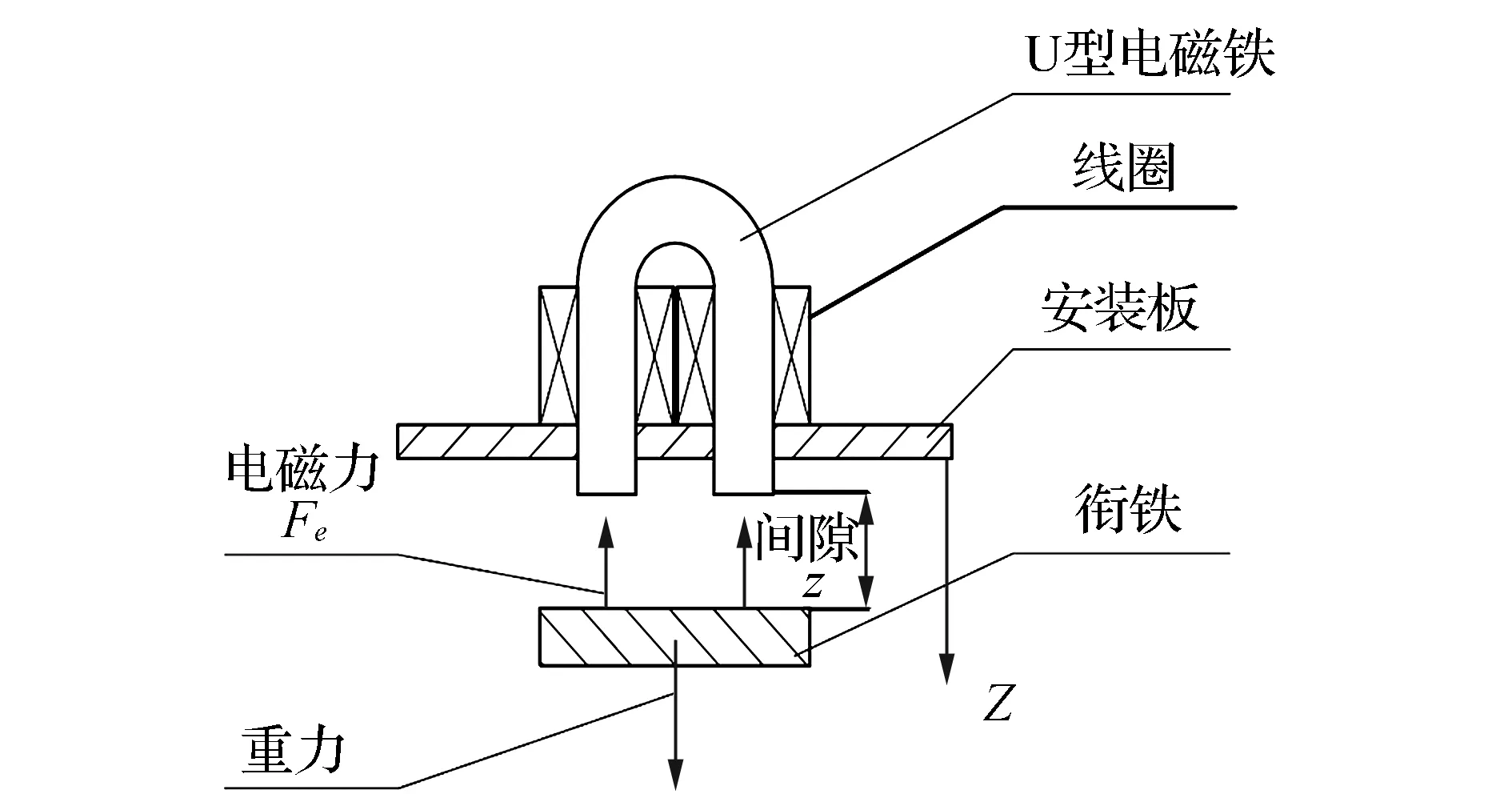
图2 磁浮式定位平台的单电磁铁模型示意图Fig.2 Schematic diagram of single magnet model for magnetic positioning stage

(1)

在工程应用中，悬浮控制算法通常采用串级控制的设计方法，将悬浮控制系统分解为电流环和间隙环两个子系统。

2.2 自抗扰控制技术

磁浮式定位平台是一个机、磁、电、热及控制耦合的复杂非线性系统，在其控制器设计中主要存在以下问题：①模型不确定性。由于系统是一个集多学科的复杂非线性系统，加之在系统运行过程中，由于系统发热等原因，使得系统的内部参数发生较大的摄动，模型具有很强的不确定性。②扰动源多且具有不可控性。磁浮式定位平台由于是一个精密的系统，故其对周边的运行环境敏感。在工作过程中，易受到由平台自身带来的电磁干扰，周边热环境，测量环节信号扰动、负载变化等干扰，可能使系统偏离正常运行的平衡点。目前针对这种复杂的多物理场耦合非线性动力学系统的研究中还没有较为成熟的建模方法和控制器设计方案，对于控制器设计目前主要是PID控制和反馈线性化控制。但是由于系统自身的原因使得工作过程中可能偏离工作平衡点，使得PID控制可能无法满足系统对精度的要求。反馈线性化由于系统精确的非线性模型，对模型误差敏感，且不能处理动态系统的未知变化，在实际系统中也很少单独使用。针对悬浮方向上的稳定悬浮控制问题引入自抗扰控制，来解决模型不确定性、测量环节存在扰动以及负载扰动等常见的控制问题。

自抗扰控制技术是一种弱依赖于系统模型的新型控制技术[23-25]，它利用非线性跟踪微分器安排过渡过程，通过扩张状态观测器实时估计出系统内外的总和扰动，并予以前馈补偿。结合磁浮式定位平台特点，主要针对二阶间隙环系统引入自抗扰控制技术，利用跟踪微分器来为系统安排过渡过程和提取系统的速度信号；利用三阶扩张状态观测器来实时估计磁浮定位平台在运行过程中的模型参数摄动、外部扰动以及电流环的不确定量叠加的效应。再利用PID控制算法来实现对磁浮式定位平台非线性系统的控制。

谢云德在韩京清等人的研究基础上，用等时区的方法确定最速离散二阶系统的线性区域的边界，以开关曲线和边界曲线来界定控制量的线性变化，区分可达区和线性区，得到最速系统综合函数，记为u=newfast3ex(x1,x2,r,h)。由于其能够有效地获取微分信号且其算法中不包含任何根号运算，有利于在过程实际中得到应用[26]。其算法具体如下：

1)若x1x2≥0，则u=-rsgn(x1+hx2)；

2)确定线性区域的边界如下：

3)若|x1|≥xb，则u=-rsgn(x1)；若|x1|≤xa，则u=-rsgn(x2)；

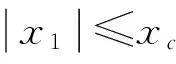
为了说明这种离散跟踪微分器对谐波信号的跟踪、微分信号提取能力，以下将对3种跟踪微分器的算法进行比较，其算法分别记作Fhan，Levant，Newfast3ex。给定信号为V(t)=1+sin(wt)+γ(t)，取h=0.005，r=200，c0=5，w=3，γ(t)为强度为0.001的均匀分布的白噪声。跟踪信号的对比见图3，微分信号的对比见图4。

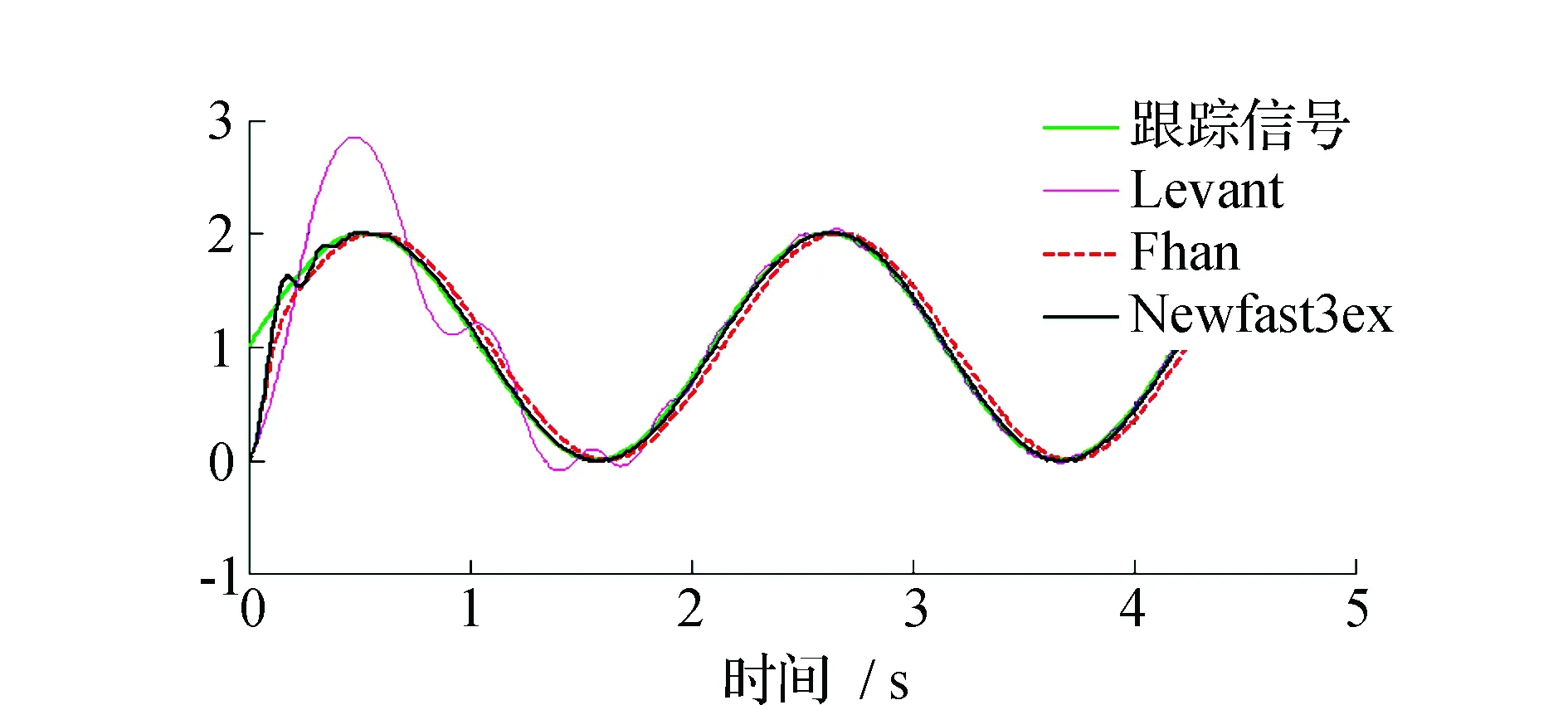
图3 跟踪信号对比Fig.3 Comparison in tracking signal for three algorithms

图4 微分信号对比Fig.4 Comparison in differential signal for three algorithms

对3种算法仿真结果表明，算法Levant存在较大的颤振，特别是微分信号的提取存在较大的误差；算法Fhan和算法Newfast3ex的信号跟踪与微分提取能力相近，但是算法Fhan存在较大的时滞现象。由于算法Newfast3ex不存在复杂的根号运算且能够方便地改变特征点来改变边界，从而提高信号跟踪以及微分提取能力，对实际工程应用来说是十分方便的。故在自抗扰控制中，将选择这种跟踪微分器来安排过渡过程与系统速度信号的提取。

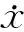
(2)

按照韩京清的方法，对这个被扩张的系统建立如下状态观测器：

(3)

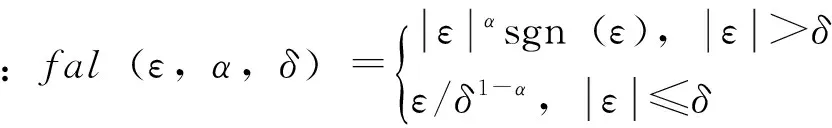
扩张状态观测器是一个动态过程，它只利用了原对象的输入和输出信息，没有用到描述对象传递关系的函数的任何信息。在选取扩张状态观测器参数的过程中，以往都是利用试凑法来选取，本文利用状态观测器的设计方法，对磁浮式定位平台单电磁铁非线性模型进行在平衡点附近线性化展开，然后依据观测器设计理论来选取β01,β02，简化了扩张状态观测器参数选定的复杂性。

3 系统仿真与实现

典型的自抗扰控制器是由过渡过程的安排、扩张状态观测器、状态误差的反馈形式、扰动估计的补偿4部分组合而成的，在本文设计的过程中，状态误差反馈采用线性PID控制的形式，其余部分如上述部分所示，其二阶间隙环自抗扰控制设计见图5。其中v1,v2分别为给定信号v的跟踪信号与微分提取信号；z1,z2分别为跟踪输出间隙y及其微分信号；z3为系统总和扰动的跟踪信号。在仿真与实验过程中，选取补偿因子b≈1～1.5，通过对平衡点附近线性化展开，利用极点配置以及状态观测器设计方法确定PD环节的参数与三阶ESO的参数选取，与电流环结合形成最终的控制量。

图5 二阶间隙环自抗扰控制设计示意图Fig.5 Schematic diagram of gap-loop’s ADRC

磁浮式定位平台自抗扰控制仿真结果见图6～图11。仿真过程中，磁浮式定位平台悬浮高度为8 mm，稳定悬浮间隙为4 mm。在仿真过程中，ESO的参数选择为β01=392,β02=40 061,β03=100 000。图6为磁浮式定位平台单电磁铁模型在内部参数发生改变时的悬浮间隙图；图7为对给定间隙值施加干扰时的悬浮间隙图；图8～图11分别为系统负载改变值为总负载的20%与40%情况下的悬浮间隙图以及由扩张状态观测器观测到的总和扰动图。

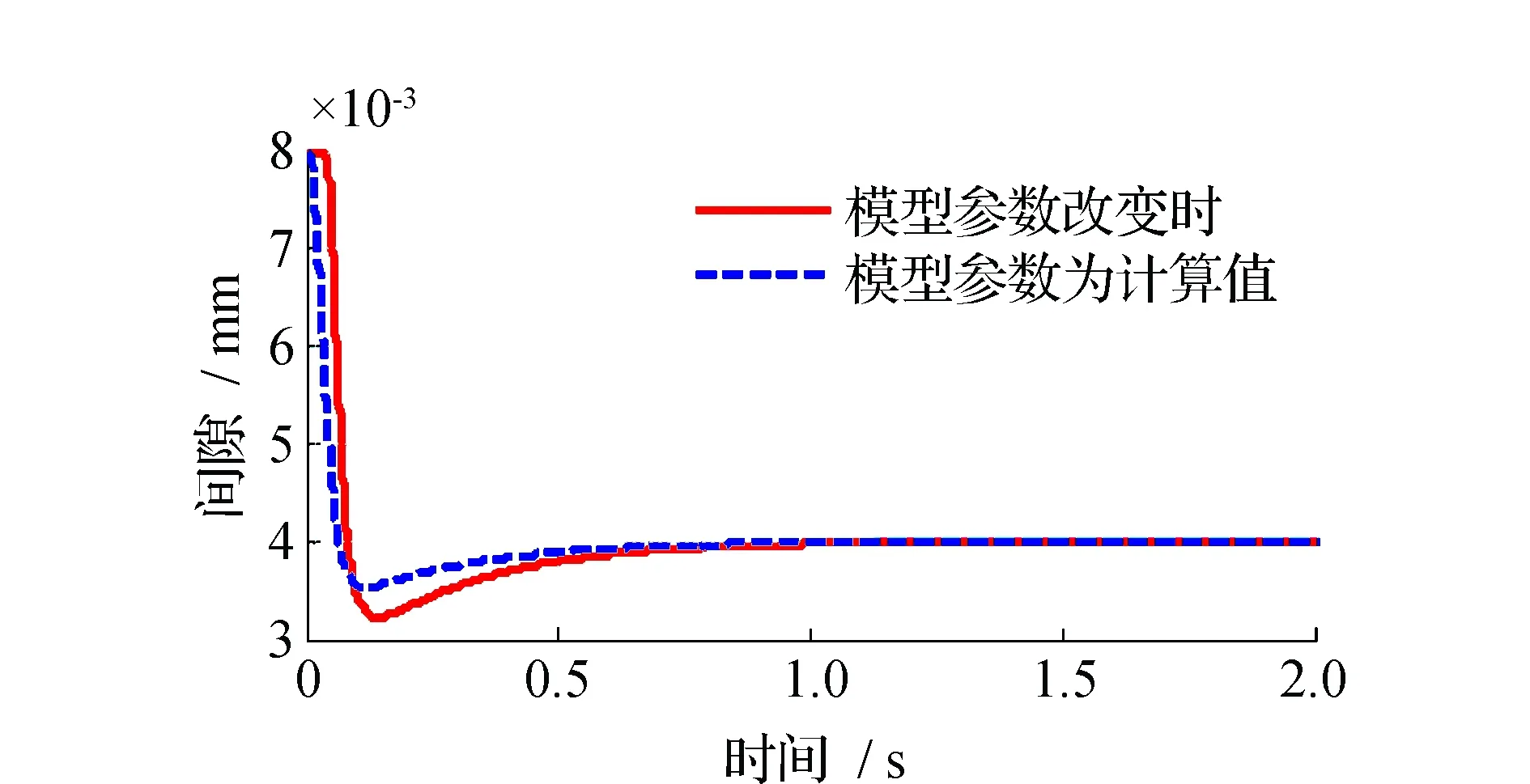
图6 模型参数改变悬浮气隙响应曲线Fig.6 Levitation gap response curve when model parameters change

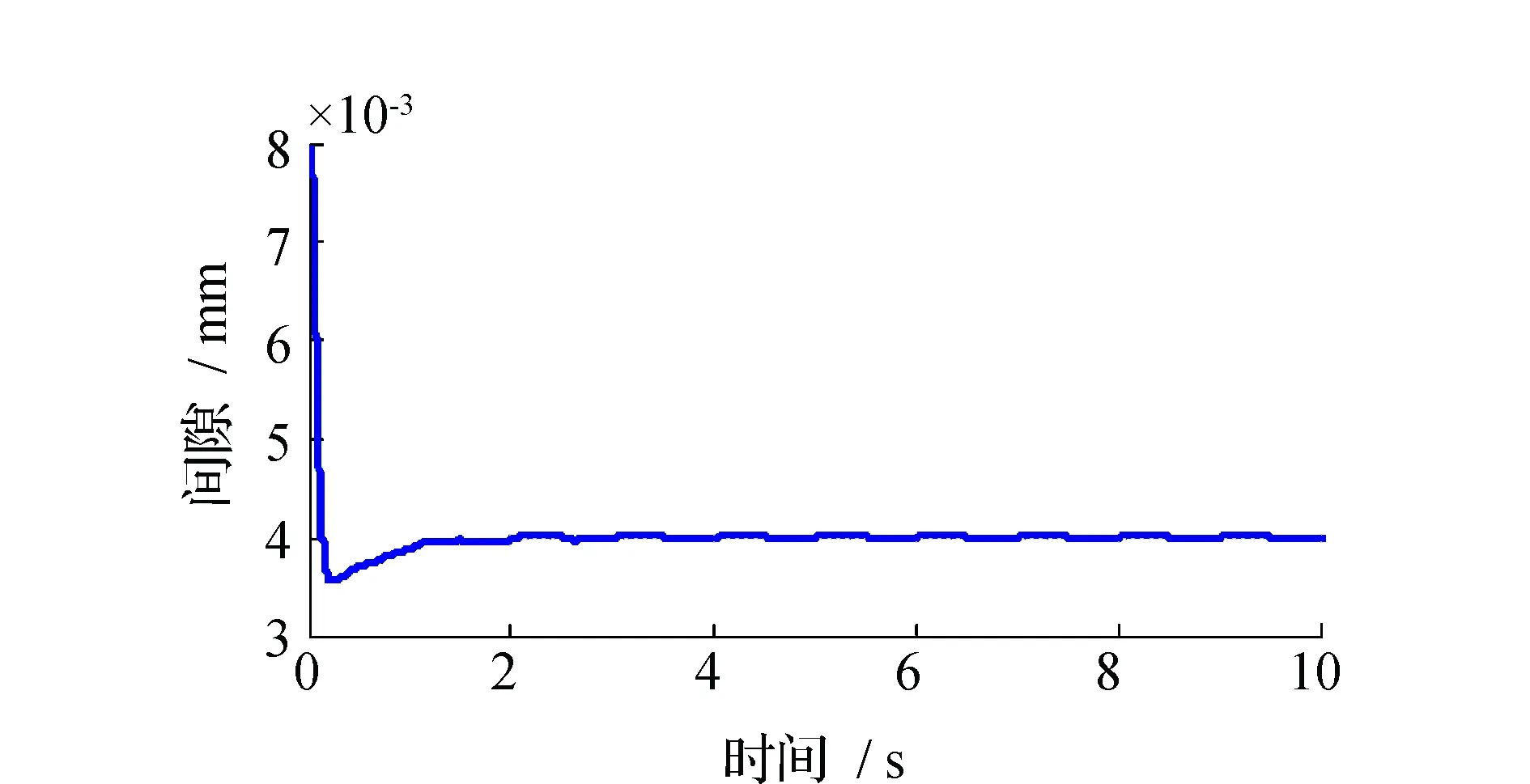
图7 间隙干扰情况下悬浮气隙响应曲线Fig.7 Levitation gap response curve when exit the gap disturbance

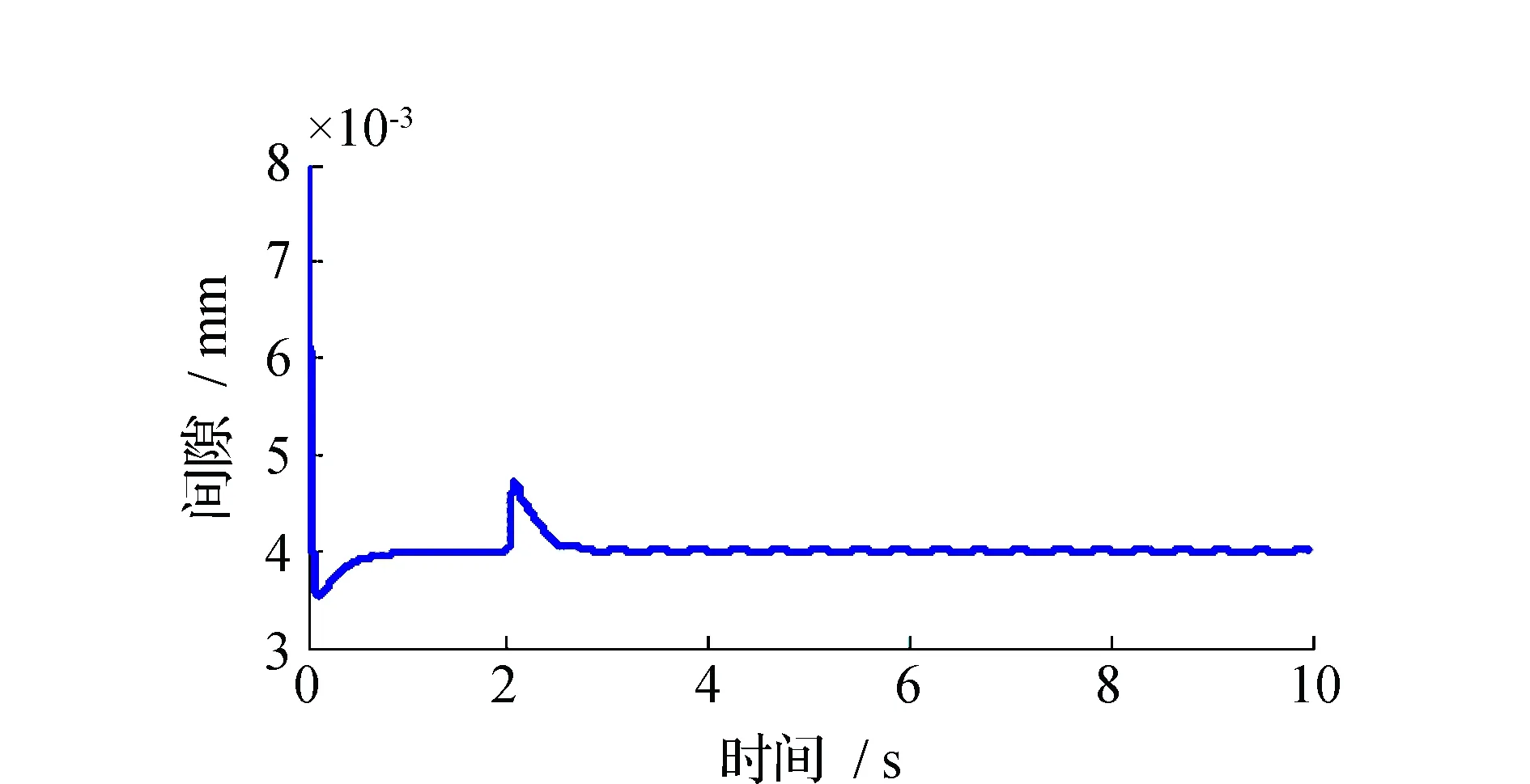
图8 负载变化20%时悬浮气隙响应曲线Fig.8 Levitation gap response curve when load changes 20%

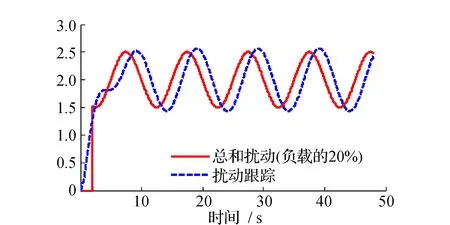
图9 负载变化20%时有扩张状态观测器获取的扰动跟踪曲线Fig.9 Disturbance tracking curve when load changes 20%

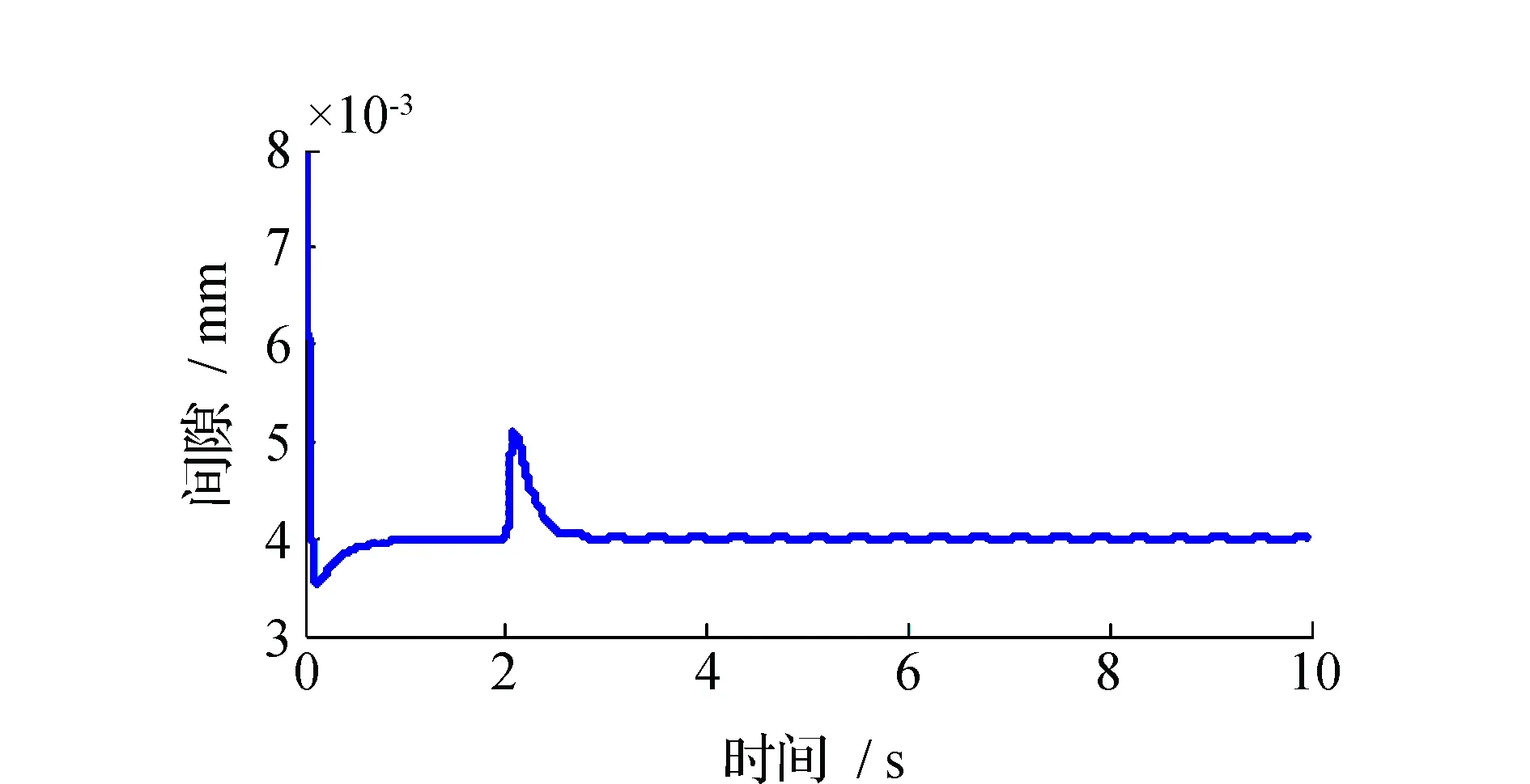
图10 负载变化40%时悬浮气隙响应曲线Fig.10 Levitation gap response curve when load changes 40%

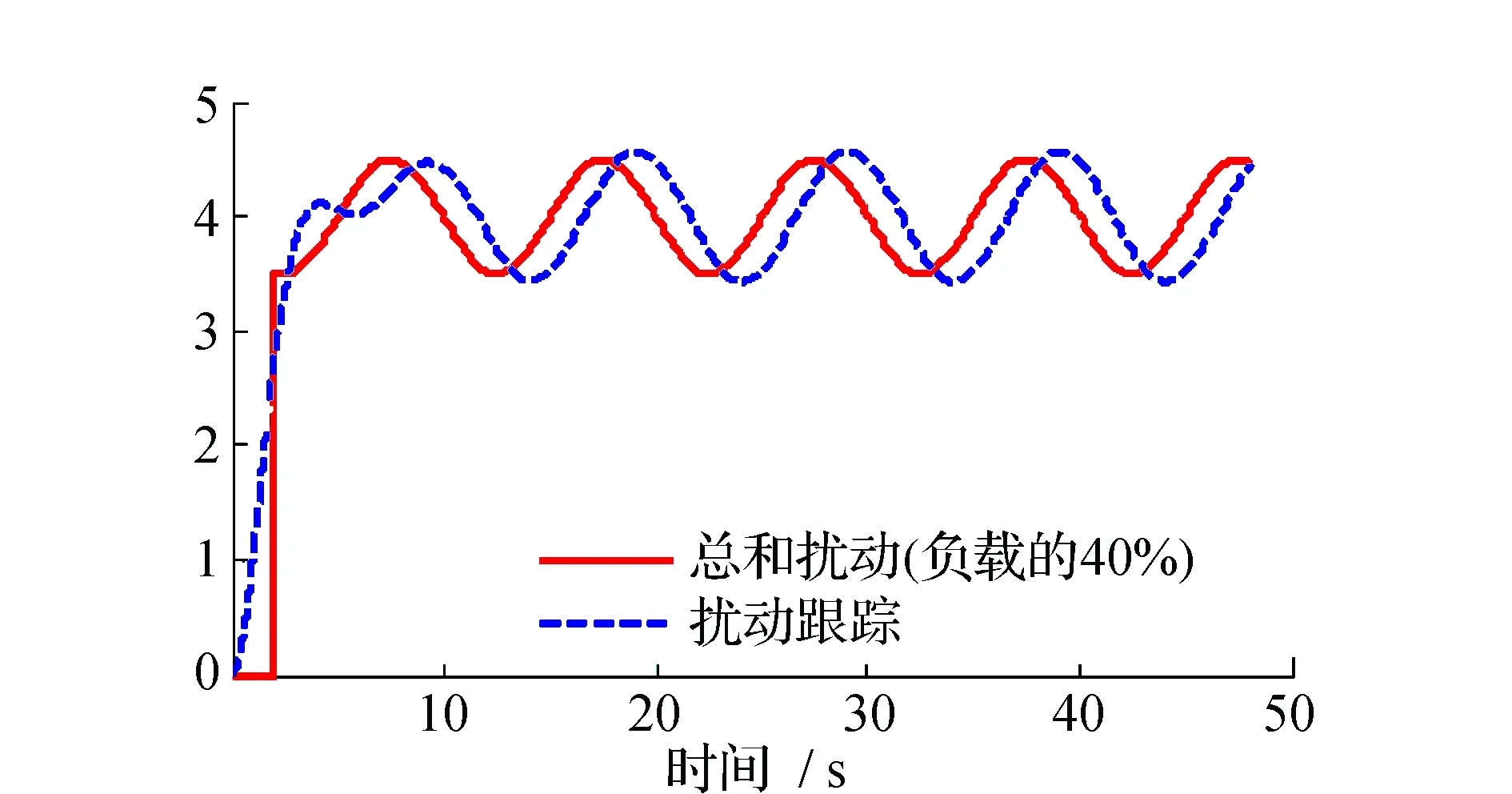
图11 负载变化40%时有扩张状态观测器获取的扰动跟踪曲线Fig.11 Disturbance tracking curve when load changes 40%

通过以上的仿真曲线可见，对磁浮式定位平台单电磁铁模型引入自抗扰控制，电磁铁悬浮系统能够正常稳定悬浮。图6表明，在磁浮式定位平台内部参数发生一定程度变化时，自抗扰控制仍能保证系统的正常稳定悬浮；图7表明，对给定信号进行施加干扰的情况下，系统在稳定后还存在一定的微小幅度的振荡，但是振荡幅度较小，对最终的稳定悬浮的影响较小；图8和图9表明，磁浮式定位平台在力的冲击干扰下，主要通过改变系统的负载来实现，悬浮系统能通过扩张状态观测器从一定程度上观测到扰动，并且对这个扰动进行补偿，使得最终的单电磁铁仍能稳定悬浮，但是扩张状态观测器观测到的扰动存在一定时延与幅度的差异，这可能与参数整定、系统频率等存在一些联系，但不影响最终的悬浮稳定。图10和图11同理。由以上分析可知，自抗扰控制能够通过各个环节的配合，使系统存在内部参数变化，力的冲击干扰的情况下仍能实现较好的稳定悬浮。

在实验过程中，实验平台上设定的悬浮气隙给定值为3 mm，故实际在示波器中显示的悬浮稳定值应该在0附近。实验平台中的磁浮小车在间隙干扰和负载突变(负载增加30%)的情况下，利用自抗扰控制得到的最终的悬浮稳定响应曲线见图12和图13。

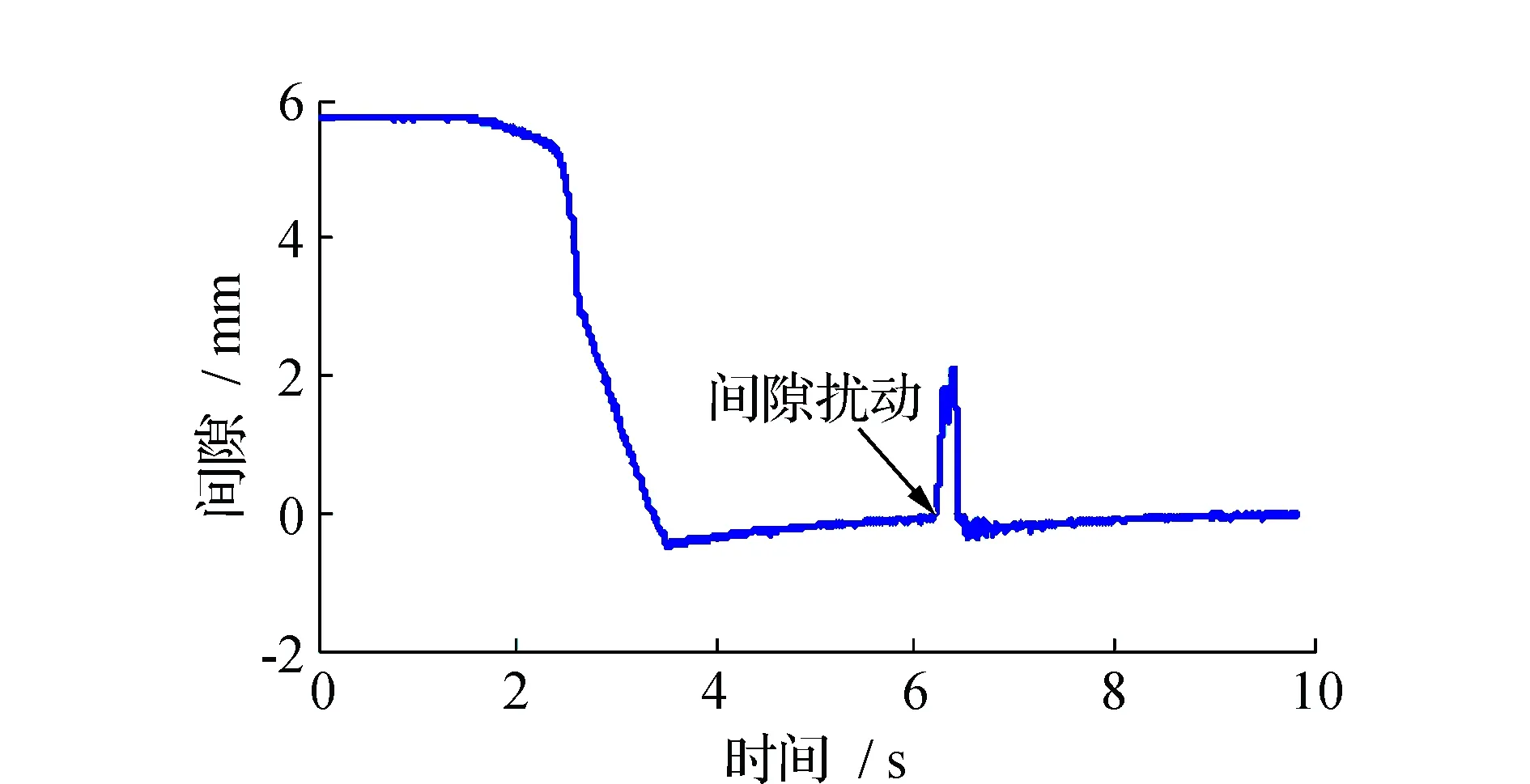
图12 磁浮定位平台在间隙扰动情况下间隙实验响应曲线Fig.12 Levitation gap response curve in the experiment when exit the gap disturbance

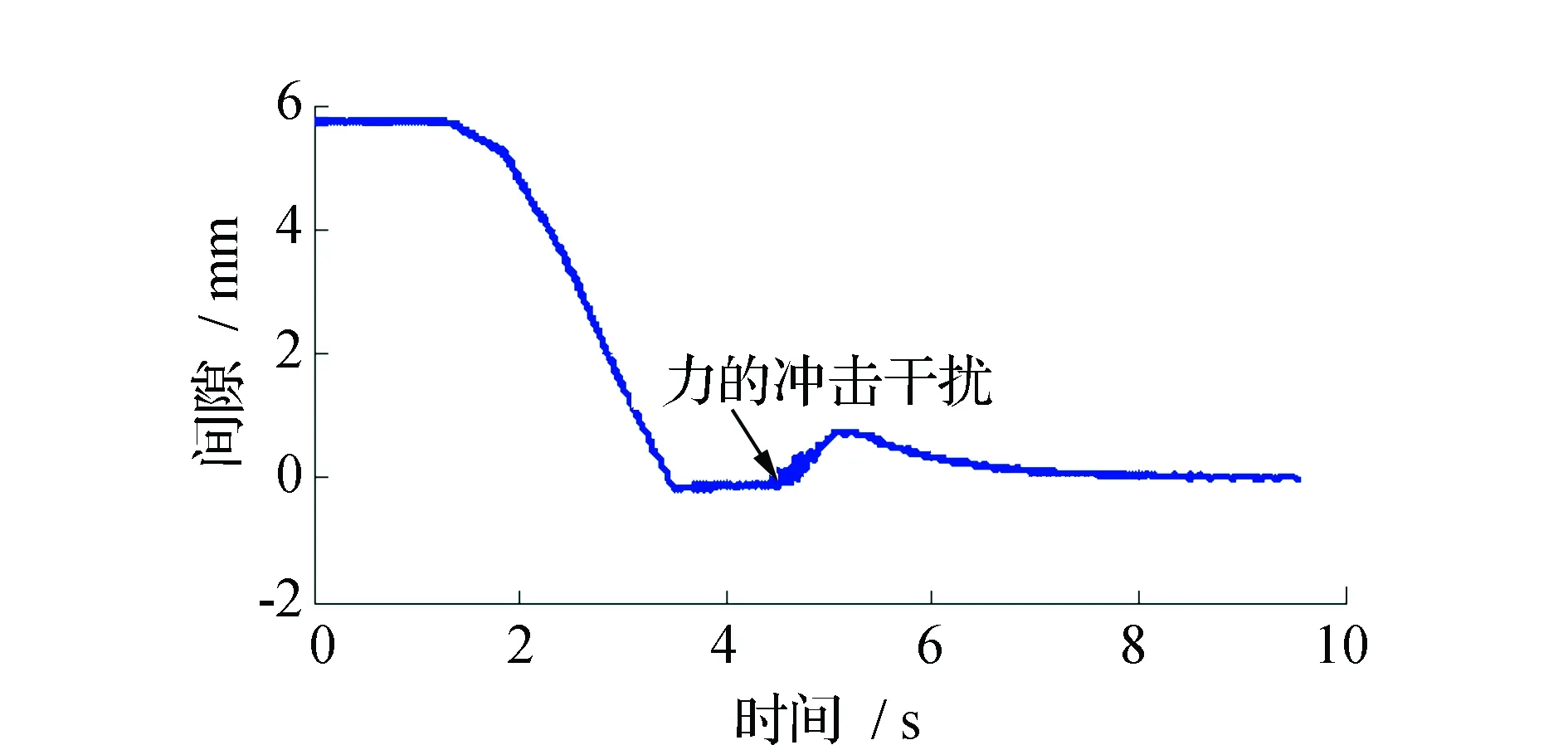
图13 磁浮小车在力的冲击干扰情况下间隙实验响应曲线Fig.13 Levitation gap response curve in the experiment when exit the load disturbance

由实验响应曲线可见，在实际系统中，通过利用自抗扰控制，磁浮定位平台能够实现稳定的悬浮，且当磁浮定位平台存在间隙阶跃干扰、负载突变干扰的情况下，磁浮定位平台系统仍能在干扰存在的情况下实现稳定悬浮，证明了自抗扰控制技术的有效性。

4 结 论

磁浮式定位平台利用磁悬浮技术实现了运动平台与驱动机构之间的无接触运动，提高了定位平台的精度以及运动行程范围。针对单运动部式的磁浮式定位平台设计了一种三点悬浮式定位平台机构。在建立平台单电磁铁模型的基础上，针对磁浮式定位平台垂直方向上的悬浮控制问题引入自抗扰控制，仿真与实验结果表明，此控制算法能实现定位平台的稳定悬浮，且在模型内部参数变换，间隙干扰、负载变动时通过控制策略的配合系统仍能实现稳定悬浮。

[1]宋文荣，于国飞，孙宝玉，等. 微电子制造领域的磁悬浮精密定位平台的结构设计研究[J]. 光学精密工程，2002，(3):271-275.

[2]孙麟治，李鸣鸣，程维明，等. 精密定位技术研究[J]. 光学精密工程，2005，(13):69-75.

[3]秦新燕，雷 金. 磁悬浮定位平台的研究综述[J]. 机床与液压，2012，(40):160-166.

[4]雷 勇，陈本永，杨元兆，等. 纳米级微动工作台的研究现状和发展趋势[J]. 浙江理工大学学报，2006(23):72-75.

[5]Zhou D F, Hansen C H, Li J. Suppression of maglev vehicle-girder self-excited vibration using a virtual tuned mass damper [J]. J. Sound Vib., 2011，(330): 883-901.

[6]Wai R J, Lee J D, Chuang K L. Real-Time PID control strategy for maglev transportation system via particle swarm optimization [J]. IEEE Trans. Ind. Electron., 2011，(58):629-646.

[7]龙志强,洪华杰,周晓斌. 磁浮列车的非线性控制问题研究[J].控制理论与应用，2003，(3):399-402.

[8]龙志强,吕治国,常文森. 基于模糊故障树的磁浮列车悬浮系统故障诊断[J].控制与决策,2004，(2):139-142.

[9]谢云德，龙志强. 高精度快速非线性离散跟踪微分器[J]. 控制理论与应用，2009，(2):127-132.

[10]Kim W J, Trumper. High-precision magnetic levitation stage for photolithography [J]. Precision Engineering, 1998，(22):66-77.

[11]Kim W J, Shobhit V, Huzefa S. Design and precision construction of novel magnetic-levitation-based multi-axis nanoscale positioning systems[J]. Precision Engineering, 2007,(31):337-350.

[12]Kim W J, Hu Tiejun, Nikhi D.Bhat. Design and control of a 6-DOF high-precision integrated positioner[C]. Preceeding of the 2004 American Control Conference Boston, 2004:2 493-2 498.

[13]Shobhit V, Kim W J, Huzefa S. Multi-axis maglev nanopositioner for precision manufacturing and manipulation applications [J]. IEEE Transactions on Industry Application,2005:486-491.

[14]Ho Y, Kim W J. A compact hall-effect-sensing 6-DOF precision positioner[J]. IEEE/ASME Transactions on Mechatronics, 2010，(6):982-985.

[15]Shan Ximin, Kuo Shihkang, Zhang Jihua, et al. Ultra precision motion control of a multiple degrees of freedom magnetic suspension stage[J]. IEEE/ASME Transactions on Mechatronics,2002,(1): 67-78.

[16]陈本永, 陈 军, 杨 涛，等. 电磁悬浮微驱动器的快速跟踪模糊控制[J]. 计算机测量与控制, 2009,(17):668-671.

[17]郑学强，张佳楫，梅雪松，等. 一种新型磁悬浮工作平台的结构设计与特性分析[J]. 中国科技论文在线，2010,(8):651-655.

[18]曹家勇,朱 煜，汪劲松，等. 平面电动机计、控制与应用技术综述[J]. 电工技术学报， 2005,(20):2-8.

[19]周 赣, 黄学良, 柏 瑞，等. 磁悬浮平面电机的解耦控制策略[J]. 中国机电工程学报, 2009,(12):81-86.

[20]姜恩泽. 磁悬浮平面电机建模与运动控制研究[D].北京：清华大学,2011.

[21]寇宝泉, 张 鲁, 李立毅. 复合电流驱动永磁同步平面电机的设计方法[J]. 中国机电工程学报, 2011，(21):110-118.

[22]崔 鹏，李 杰，张 锟. 基于补偿反馈线性化的悬浮控制器设计[J]. 铁道学报，2010,32(2)：121-125.

[23]Han Jingqing. Active Disturbance Rejection Control: the technique for estimating and compensating the uncertainties[M]. National Defence Industry Press, 2008.

[24]Han Jingqing. From PID to active disturbance rejection control [J]. IEEE Transactions on Industrial Electronics, 2009,56(3):900-906.

[25]Tian G, Gao Z Q. Benchmark tests of active disturbance rejection control on an industrial motion control platform [C]// Proceeding s of the 2009 American Control Conference. St. Louis, MO: IEEE, 2009:5 552-5 557.

[26]谢云德，李云钢，龙志强，等. 一种基于边界特征曲线且特征点可变的二阶非线性离散跟踪微分器及在测速定位系统中的应用[J]. 自动化学报，2014,(40):952-964.

Control of high-precision magnetic levitation positioning stage

ZHANG He-Hong， LONG Zhi-Qiang*

(College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073,China)

High-precision stage is the key component in the scene of micro-technology including photoetching machine, nano-measurement,process and micro-assemble, etc. Magnetic levitation positioning becomes the hot topic in positioning technology due to using non-contact maglev technology in motion stage and driving part, which can eliminate friction and attrition to motion and improve the precision. The development and researches of magnetic positioning stage in China and abroad are introduced and a new structure of magnetic levitation positioning stage is presented. Considering the uncertainty of the model and gap and load disturbance, active disturbance rejection control is proposed to maglev positioning stage for the problem of stable levitation control based on the single magnet model. The simulation and experiments show that the method meets the demands of high-precision and stable levitation control and has the strong ability of robust anti-disturbance.

magnetic levitation; positioning stage; active disturbance rejection control

10.13524/j.2095-008x.2015.03.052

2015-05-13

国家科技支撑计划资助项目(2013BAG19B01)

张和洪(1990-)，男，福建福州人，硕士研究生，研究方向：磁浮控制技术，E-mail:hehongzhangnudt@hotmail.com;*通讯作者：龙志强(1967-),男，江西吉安人，研究员，博士，博士研究生导师，研究方向：磁浮控制技术、故障诊断与容错控制等，E-mail:lzq@maglev.cn。

TH703.8

A

2095-008X(2015)03-0084-09