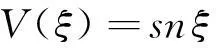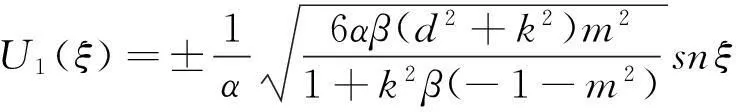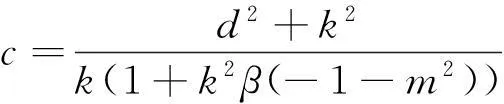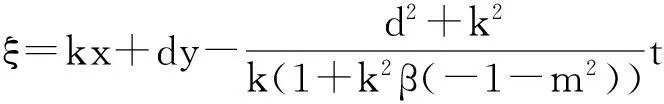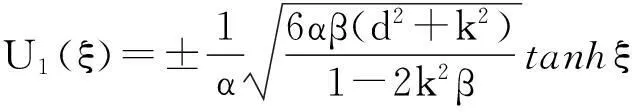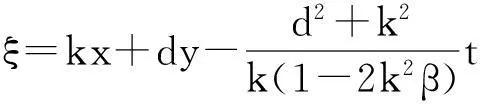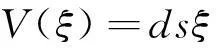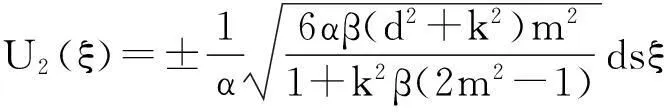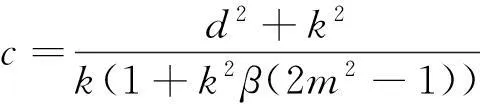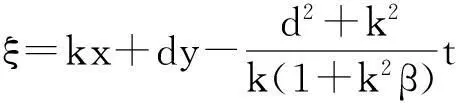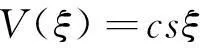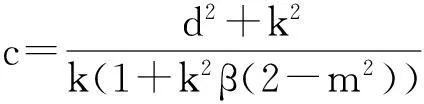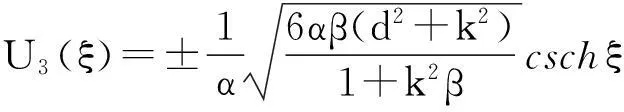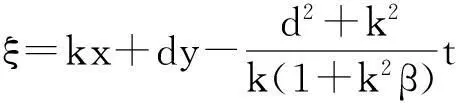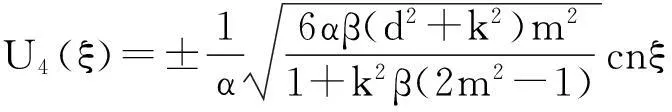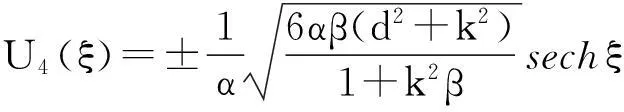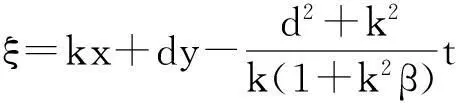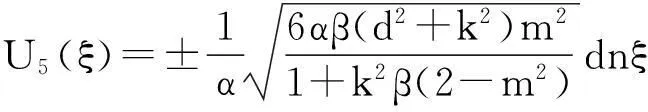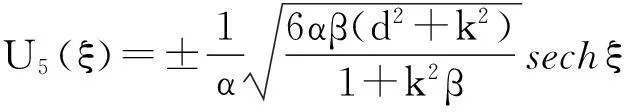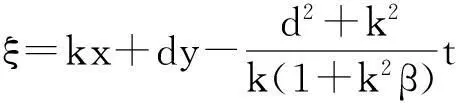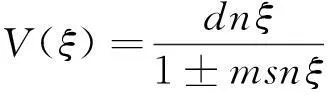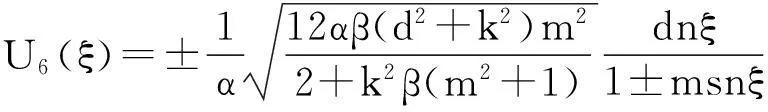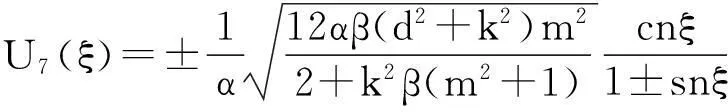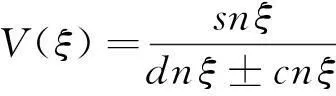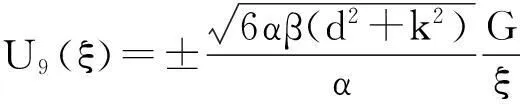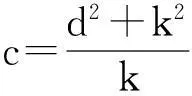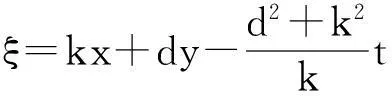广义二维BBM方程的精确解研究

方　芳，胡贝贝，陶庭婷

广义二维BBM方程的精确解研究

方芳，胡贝贝，陶庭婷

摘要:利用辅助方程法并借助符号计算软件Maple求解了具有高阶非线性项的广义二维BBM方程，并获得该方程丰富的精确行波解，其中包括三角函数解、双曲函数解、双周期Jacobi椭圆函数解。

关键词:BBM方程，辅助方程法，三角函数解，双曲函数解，双周期Jacobi椭圆函数解

1引言

非线性方程被广泛应用于许多研究领域，非线性方程解的研究在非线性科学领域起着重大作用，对于非线性系统没有固定的求解方法，目前已经发展了很多的求解方法，如双曲正切函数法[1]、齐次平衡法[2]、tanh函数法[3]、Fan子方程法[4]、sine-cosine方法[5]、李群方法[6]等。

1972年，Benjamin等[7]提出了BBM方程

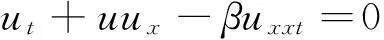
(1)

张卫国[8]在1996年提出了改正的BBM方程

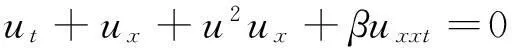
(2)

之后，吕大昭[9]运用Jacobi椭圆函数展开法研究了改正了的BBM方程，得到了更多的周期解。在2006年，黎明[10]又做了进一步的推广，得到了广义BBM方程

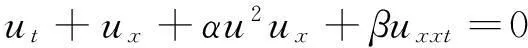
(3)

并求出了它的有界行波解。

本文将方程(3)进一步推广到一般的广义二维BBM方程

(4)

并利用与文献[11]不同的方法——辅助方程法[12-14]对方程(4)进行了研究，获得该方程一系列精确行波解。

2广义二维BBM方程的精确行波解

为求得方程(4)的解，我们做如下行波变换

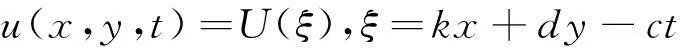
(5)

这里c是波速，k,d,c为常数，将(5)式代入方程(4)，并关于ξ积分两次得

(6)

设方程(6)的解形式为

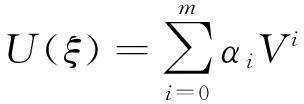
(7)

其中V(ξ)为辅助方程且满足：

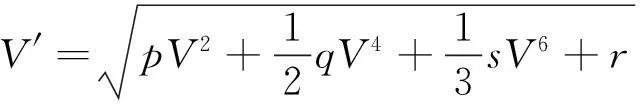
(8)

这里p,q,s和r为任意常数。平衡方程(6)中的u3和u′′得m=1，即方程(6)解的形式为

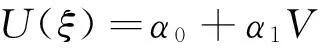
(9)

把(8)、(9)式代入(6)式，令形如Vi(i=0,1,2,3,4,5)的项的系数全部为零，得到一组关于α0,α1,p,q,s,r,k,d,c的代数方程

(10)

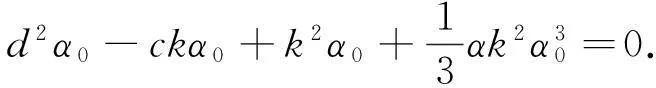
借助符号计算软件Maple，由(10)得

(11)

所以方程(6)的解为

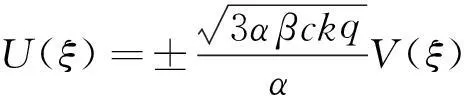
(12)

这里V(ξ)满足方程(8)。

由于辅助函数V(ξ)的参数p,q,s和r的取值不同有以下九种情况(其中m(0

1.当p=-(1+m2),q=2m2,s=0,r=1时，方程(8)有一个双周期椭圆函数解

(13)

从而由(11)、(12)和(13)可得方程(4)对应的解为

(14)

当m→1时，得到对应的扭波解和反扭波解

(15)

2.当p=2m2-1,q=2,s=0,r=-m2(1-m2)时，方程(8)有一个双周期椭圆函数解

(16)

(17)

当m→1时，得到对应的扭波解和反扭波解

(18)

3.当p=2-m2,q=2,s=0,r=1-m2时，方程(8)有一个双周期椭圆函数解

(19)

从而由(11)、(12)和(19)可得方程(4)对应的解为

(20)

当m→1时，得到对应的扭波解和反扭波解

(21)

4.当p=2m2-1,q=-2m2,s=0,r=1-m2时，方程(8)有一个双周期椭圆函数解

(22)

从而由(11)、(12)和(22)可得方程(4)对应的解为

(23)

当m→1时，得到对应的扭波解和反扭波解

(24)

5.当p=2-m2,q=-2,s=0,r=m2-1时，方程(8)有一个双周期椭圆函数解

(25)

从而由(11)、(12)和(25)可得方程(4)对应的解为

(26)

当m→1时，得到对应的扭波解和反扭波解

(27)

(28)

从而由(11)、(12)和(28)可得方程(4)对应的解为

(29)

(30)

从而由(11)、(12)和(30)可得方程(4)对应的解为

(31)

(32)

从而由(11)、(12)和(32)可得方程(4)对应的解为

(33)

9.当p=0,q=2,s=0,r=0时，方程(8)有一个双周期椭圆函数解

(34)

从而由(11)、(12)和(34)可得方程(4)对应的解为

(35)

其中G为常数。

[参考文献]

[1]W. Malfliet. Solitary wave solutions of nonlinear wave equations[J]. America Journal Physics, 1992, 60(7):650-654.

[2]M. L. Wang et al. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Physics Letters A, 1996, 216(1):67-75.

[3]Z. Y. Yan. New explicit traveling wave solutions for two new integrable coupled nonlinear evolution equations[J]. Physics Letters A, 2001, 292:100-106.

[4]E. G. Fan. Uniformly constructing a series of explicit exact solutions to nonlinear equation in mathematical physics[J]. Chaos, Solitons and Fractals, 2003, 16:819-839.

[5]A. M. Wazwaz. The tanh method and a variable separated ODE method for solving double sine-Gordon equation[J]. Phys. Lett. A,2006,350:367-370.

[6]P. J. Olver. Applications of Lie groups to differential equations[M].New York: Springer-Verlag,1993.

[7]Benjamin T B,Bona J L.Model equations for long waves in nonlinear dispersive systems[J]. Philos Trans R Soc,1972,272:A47-78.

[8]张卫国. Burgers与组合KdV混合型方程的精确解[J].数学物理学报,1996,16(3):241-248.

[9]吕大昭.非线性发展方程的丰富的Jacobi椭圆函数解[J].物理学报,2005,54(10):4501-4504.

[10]黎明. 广义BBM方程的有界行波解[J]. 四川师范大学学报,2007,30(4):478-480.

[11]胡贝贝,唐清干,王琼,元艳香. 广义二维BBM方程的精确行波解[J].桂林电子科技大学学报,2013,33(4):335-338.

[12]S. Zhang, W. Wang, J. L. Tong. The improved sub-ODE method for a generalized KdV-mKdV equation with nonlinear terms of any order, Phys. Lett. A ,2008, 372:3808-3813.

[13]X. Q. Liu, H. L. Chen, Y. Q. Lu. Explicit solutions of the generalized KdV equations with higher order nonlinearity[J]. Applied Mathematics and Computation, 2005, 171(1): 315-319.

[14]胡贝贝,冯大河,唐清干. 基于辅助方程法对Gardner-KP方程精确行波解研究[J].安庆师范学院学报,2012,18(4):11-14.

责任编辑：刘海涛

收稿日期：2014-03-19

基金项目：滁州学院科研启动基金(2014qd009；2014qd006；2014qd008)：滁州学院科研项目(2014GH12)：安徽省教育厅一般科研项目(KJ2013B188)

作者简介：方芳，胡贝贝，陶庭婷，滁州学院数学与金融学院教师(安徽 滁州 239000)。

中图分类号:O175. 1

文献标识码：A

文章编号：1673-1794(2015)02-0020-04