不同厚度纳米Ti薄膜的力学性能

王海斗,董美伶,,崔秀芳, 邢志国, 朱丽娜, 刘金娜,

(1 装甲兵工程学院 装备再制造技术国防科技重点实验室，北京 100072; 2 哈尔滨工程大学 材料科学与化学工程学院，哈尔滨 150001; 3 中国地质大学(北京) 工程技术学院，北京 100083)



不同厚度纳米Ti薄膜的力学性能

王海斗1,董美伶1,2,崔秀芳2, 邢志国1, 朱丽娜3, 刘金娜1,2

(1 装甲兵工程学院 装备再制造技术国防科技重点实验室，北京 100072; 2 哈尔滨工程大学 材料科学与化学工程学院，哈尔滨 150001; 3 中国地质大学(北京) 工程技术学院，北京 100083)

通过直流磁控溅射方法制备出四个不同厚度的纳米Ti薄膜，并分别采用纳米压痕仪、电子薄膜应力分布测试仪研究了Ti薄膜的力学性能和残余应力大小，结合分形维数方法和原子力显微镜对薄膜表面粗糙度和表面形貌进行了分析。实验结果表明：随Ti薄膜厚度的增加，薄膜晶粒尺寸逐渐增大，表面粗糙度和残余应力值随厚度的增加先增大后减小，而Ti薄膜弹性模量和硬度随薄膜厚度增加呈现出先减小随后增大的趋势。当薄膜厚度为600，2400，3600nm时薄膜中存在残余压应力，厚度为1200nm时存在残余拉应力，薄膜中残余应力分布最为均匀，但此时薄膜具有较低的硬度和弹性模量值。分析得出Ti薄膜中存在残余拉应力会使薄膜硬度和弹性模量值变小，残余压应力反之。

薄膜；纳米压痕；分形维数；力学性能

随着薄膜光学器件和薄膜电子器件的广泛应用。薄膜材料和薄膜技术已成为当代材料科学中最活跃的研究领域之一[1]。因受到尺寸效应的限制和应用需求的制约，目前对金属薄膜的研究多集中在电学、光学以及各种物理性能上，而对金属薄膜的力学性能的研究较少，为保障金属薄膜的可动微器件的稳定运行和长久寿命, 研究纳米金属薄膜的形貌结构、力学特性十分必要的[2,3]。

纳米压痕技术可以在微观尺度范围内更深入地了解薄膜的纳米力学性能，在压痕过程中即可获得反映硬度和弹性模量的连续的载荷-位移关系曲线，并可以在不分离薄膜的情况下直接测试超薄甚至极软的薄膜材料的性能，避免了压痕边缘模糊和基体影响等传统硬度检测技术的一些缺点。Oliver等[4,5]完善了纳米压痕测试理论，纳米压痕仪在样品的质量检测、纳米薄膜的性能测试以及摩擦化学反应膜的监测评估等方面都得到了广泛的应用[6，7]，成为目前计算材料力学性能的主要依据。

现有的测量薄膜应力的方法，有X射线法、Raman光谱法、曲率法等[8-10]。由于X射线分析法仅适用于具有晶格的半导体薄膜和晶体薄膜的测量，并且对涂层的厚度有一定要求，基本不能实现薄膜材料的在线测量[11]；拉曼光谱法又存在荧光干扰，检测灵敏度低[12,13]，因此本研究中测量薄膜中的应力选择较为常见的曲率法[14]。本实验以Ti薄膜为研究对象，研究沉积时间对Ti膜的表面形貌及力学性能和残余应力的影响，力争为高质量薄膜制备的提供参考依据。

1 实验材料与方法

1.1 薄膜的制备与测试方法

实验采用AS500DMTXB型计算机自动控制离子镀膜机沉积纯Ti薄膜，Ti靶纯度为99.99%，衬底材料为单面抛光的Si〈100〉基片。镀膜前，首先用乙醇超声波清洗基片15min，烘干后放入真空室内进行沉积。Ti薄膜的制备工艺为：Ar气流量200mL/min，背底真空为3.7×10-3Pa，偏压1000V，清洗3min。镀膜时，工作气压为0.88Pa，基底温度为300℃，沉积时间分别为1，2，4，6h。

使用OLS400型激光三维电子显微镜对不同沉积时间(1，2，4，6h)的Ti薄膜厚度进行测定，其测量精度为0.5μm，能够满足实验需求，测得薄膜厚度分别为600，1200，2400，3600nm。结果表明：在溅射功率相同的条件下，膜厚与溅射时间基本呈正比关系。这主要是因为磁控溅射的溅射功率一定时，靶材原子在基体表面的沉积速率基本不变。薄膜的表面形貌和粗糙度采用Nano SEM450/650场发射扫描电子显微镜和CSPM500原子力显微镜进行表征；使用D8型X射线衍射仪对薄膜的相结构进行分析；Nano Indenter G200纳米压痕测试仪测定力学性能；BGS6341型电子薄膜应力分布测试仪测量薄膜内部残余应力分布。

1.2 纳米压痕法原理

纳米压痕法测试环境简单，无需精细昂贵的试样准备，具有精确几何尺寸的标准压头，使得许多实验都可以在相对较小的试样上和区域内进行，因此其在测量材料力学性能方面应用广泛[15]。

根据这种方法，材料的硬度和弹性模量可以通过下面的公式得到[16]：

(1)

(2)

(3)

(4)

式中:hc为真实接触深度;hmax为最大压入深度；C0,…,C8为对曲线进行拟合后得到的参数常量；Pmax为最大压入载荷；Ac为真实接触面积；Er为等效弹性模量。

接触刚度S为卸载曲线的顶部斜率，采用以下函数对载荷-位移曲线的卸载部分进行拟合：

P=α(h-hr)m

(5)

式中：hr为卸载后的残余深度；α和m是通过实验获得的拟合参数。通常用最小二乘法拟合卸载曲线顶部的25%～50%。根据测试经验观察，对玻式压针的卸载行为可用抛物线型解m=1.5和ε=0.75近似[17]。

因此，接触刚度可以通过对公式(5)进行微分计算得出：

(6)

1.3 曲率法测量原理

薄膜沉积到基片上时，薄膜与基片之间会产生二维的界面应力，使基片发生微小弯曲。采用平行单色光使平晶平面与镀膜样品表面发生干涉，通过观察干涉条纹的变化来计算薄膜中应力的大小。可以用Stoney公式表达[18]:

(7)

式中：σ为薄膜应力；ts，tf分别为基片和薄膜的厚度；R1，R2分别为基片镀膜前后的曲率大小，其中Ms=Es/(1-vs)为基片的二维杨氏模量，Es，vs分别为基片的弹性模量和泊松比。

2 结果与分析

2.1 沉积时间对薄膜表面形貌和晶粒尺寸的影响

图1所示为0.88Pa、300℃条件下沉积2h获得的纯Ti薄膜表面形貌的二维图像。从图中可以看出薄膜表面结构致密平整，薄膜由岛状颗粒和空洞组成。

图1 厚度为1200nm薄膜的二维表面形貌图 (a)SEM;(b)AFMFig.1 Two dimension surface morphology of Ti film at 1200nm (a)SEM;(b)AFM

2.1.1 原子力显微镜分析

从图2可以看出不同厚度的薄膜表面形貌和粗糙度是不同的，随着薄膜厚度的增加，薄膜的致密度逐渐提高，晶粒逐渐长大，晶粒之间的大小差别减小。沉积时间较短时，沉积表面上形成很小的岛，岛的侧面坡度相似，岛与岛之间存在一定距离。随着薄膜厚度增大，小岛纵向生长趋势明显，岛与岛之间发生团聚，晶粒逐渐变大，岛密度有所下降，晶粒大小分布更加均匀。薄膜厚度为3600nm时颗粒的平均尺寸最大，表面相对平坦。Ti薄膜表面粗糙度则随薄膜厚度的增加呈现出先增大后减小的趋势。当薄膜厚度为600nm时，薄膜粗糙度Ra= 2.78nm，薄膜厚度为1200nm时增大为4.49nm，当薄膜厚度达到2400nm时，Ti薄膜粗糙度达到最大值，Ra=8.69nm，随后随着薄膜厚度的增加出现减小趋势，当薄膜厚度为3600nm时，粗糙度Ra=4.92nm。因此薄膜厚度增加的过程中，岛尺寸的增加影响到溅射粒子在表面的迁移，使薄膜的表面形貌发生变化，使得薄膜生长表面表现出动态变化行为。

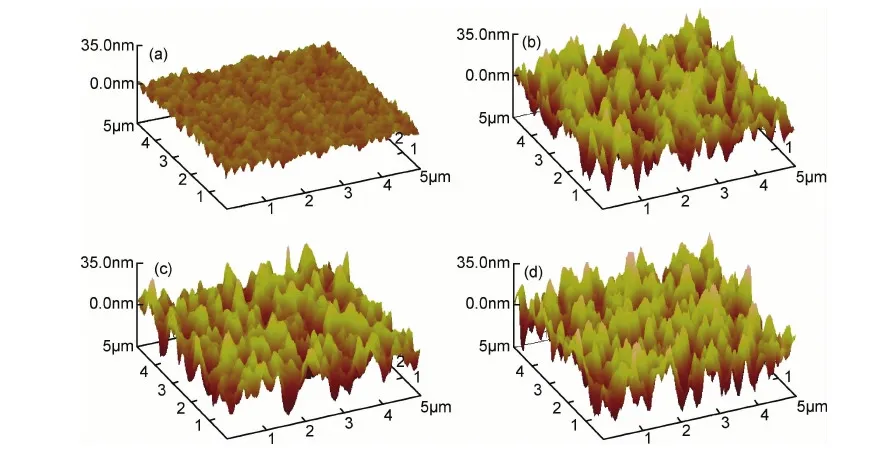
图2 不同厚度Ti薄膜表面形貌图 (a)600nm;(b)1200nm;(c)2400nm;(d)3600nmFig.2 Surface morphology at different thicknesses of Ti film (a)600nm;(b)1200nm;(c)2400nm;(d)3600nm

根据上述不同厚度的Ti薄膜表面结晶形貌和粗糙度变化，结合薄膜生长的扩散原理分析发现：厚度为600nm时的Ti薄膜，岛尺寸较小，岛密度较大，这意味着分布在表面上的岛存在粗化的驱动力，岛与岛之间将通过合并来降低单位体积的自由能。因此薄膜表面小岛尺寸逐渐增大，空洞数量减少，当薄膜厚度为3600nm时，岛尺寸最大，呈现出明显的柱状晶生长方式。可以认为磁控溅射制备的Ti薄膜的生长过程为气态的粒子与基底碰撞后，吸附在基底的表面，这些带有一定能量的粒子在薄膜表面迁移，并在合适的格点形核长大，首先是形成岛状的结构，然后岛与岛连接，生成连续的薄膜材料，通过扩散作用，按照岛状生长模式生长。

2.1.2 分形维数分析

研究表明，薄膜材料的表面存在良好的分形特征。因此，许多学者将分形理论应用于材料表面微观形貌的表征中，以期达到建立表面微观形貌与材料性能之间定量关系的目的[19-24]。分形维的计算方法有多种，如盒计维数法、功率谱密度法、分规法、面积-尺度法结构函数法等[21-25]。本工作采用盒计维数法计算AFM图的分形维数。其定义为：设A是空间的任意非空有界子集，对于任意的一个r> 0，N(rn)表示用来覆盖A所需边长为r的n维立方体(盒子)的最小数目。如果存在一个数D，使得当r→0时，有

N(rn)∝(1/rn)-D

(8)

那么称D为A的盒计维数(简称盒维数)。可以用分形维定量描述粗糙表面的整体复杂程度[22]。经简化计算，盒计维数为：

(9)

式中：rn为测度，即盒子的边长;N(rn)为测数，即边长为rn时，所用盒子的个数。

采用原子力显微镜获取不同粗糙表面的三维形貌数据(如图2所示)，薄膜表面颗粒大小不同，但这些颗粒在一定的尺度范围内均匀分布在薄膜表面上。存在小尺度的颗粒或高度调制，且这些小的颗粒或高度调制无特征大小，使得薄膜表面在一定的尺度范围内具有很明显的分形特征[26]。本工作采用盒计维数法计算薄膜表面粗糙形貌的分形维数，采样面积为5nm×5nm，用最小二乘法( least squares’ method )，在对数坐标系内对计算数据进行拟合，结果如图3所示，D为各粗糙表面的分形维数，R为数据的线性相关系数。相关系数越高，微观形貌的分形特征越明显。

图3 不同厚度的Ti薄膜表面分形维数结果图 (a)600nm;(b)1200nm;(c)2400nm;(d)3600nmFig.3 Surface fractal dimension results of different thicknesses Ti films (a)600nm;(b)1200nm;(c)2400nm;(d)3600nm

由图2可发现，薄膜表面的粗糙度随薄膜厚度的增加先增大后减小，分形维数结果却呈减小的趋势。通过分析可以知，粗糙度和分形维数都与薄膜中晶粒大小密切相关，薄膜厚度为600nm时，薄膜表面均方根粗糙度最小，但是分形维数最大，表明在大范围内，晶粒尺寸较小，而小范围内晶粒大小不均匀，空洞数量较多。随着薄膜厚度的增加空洞数量有所减少，当薄膜厚度为1200nm时，分形维数最小，粗糙度也相对较小因薄膜生长存在一个局域的平衡过程，沉积在基底表面的原子或原子团不可能在瞬间失去能量，而是在沉积点附近局部区域内扩散一定距离，调整沉积位置，同时伴随着小岛的合并和长大，最终表现为所看到的表面形貌。当薄膜厚度小时，薄膜表面岛密度相对较低，存在较多空洞，因此分形维数最大，但小岛尺寸相对较小，因此粗糙度反而最小，随薄膜厚度的增加，岛的生长与合并趋势明显，小岛尺寸逐渐变大，因此粗糙度呈增大趋势，分形维数随着空洞数量的减少，反而呈现出减小的趋势。

通过上述分析证明磁控溅射制备的Ti薄膜生长主要是通过扩散作用，按照柱状方式生长，当薄膜厚度为1200nm时，薄膜表面空洞数量最少，小范围内最为均匀。

2.2 沉积时间对薄膜成分和结晶取向的影响

图4为不同厚度Ti薄膜的XRD衍射谱，从不同厚度纯Ti薄膜的XRD图谱中可以看出，在不同厚度的纯Ti薄膜并没有发生相结构的改变，均为密排六方(hcp)结构的α-Ti。

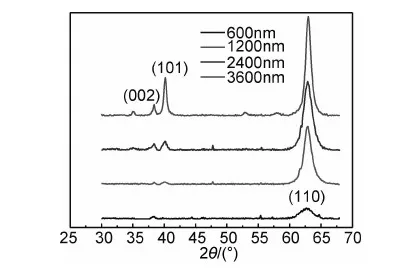
图4 不同厚度Ti薄膜的XRD衍射谱Fig.4 XRD diffraction spectra at different thicknesses of Ti film

当Ti薄膜厚度为600nm时，只出现了(002)和(110)两个衍射峰，薄膜厚度增加到1200nm时(101)衍射峰随之出现，并且衍射峰强度随着薄膜厚度的增加而增强，当薄膜厚度为3600nm时，三条衍射峰最为尖锐。因此Ti薄膜在表面自由能最小的(002)晶面方向和应变能较小的(101)晶面均有定向生长的特性，并受到来自基底取向的影响，使得Ti薄膜中(110)晶面方向上出现了较强的衍射峰。因此随着厚度的增加，Ti薄膜衍射峰强度逐渐增加。

2.3 沉积时间对薄膜力学性能的影响

利用纳米压痕仪可以直接获得材料的载荷-位移曲线。为了避免基体对薄膜性能的影响，使用纳米压痕仪测试时的压入深度不应超过薄膜厚度的1/10，因此实验固定最大压入压深为50nm，从而得到不同厚度Ti薄膜的载荷-位移曲线图，如图5所示。图中各曲线连续、光滑，没有明显的台阶和突变出现，表明在压痕实验过程中不同厚度的Ti薄膜表面平整，都没有出现裂纹。在相同压深的情况下，厚度为1200nm的Ti薄膜载荷峰值明显高于其他厚度Ti薄膜的载荷峰值，说明1200nm厚的Ti薄膜具有较强的抵抗外加载荷的能力，其抵抗塑性变形的能力最强；卸载后弹性变形得到恢复，而塑性变形保留下来，从图中可以看出薄膜厚度为1200nm时，残余深度小于其他厚度下的残余深度，说明Ti薄膜厚度为1200nm时薄膜塑性变形较小。

图5 不同厚度Ti薄膜的纳米压痕结果与残余应力分布图 (a)载荷-位移曲线图;(b)应力分布图Fig.5 Nanoindentation results and residual stress distribution at different thicknesses of Ti film (a)load-depth curves;(b)distribution of residual stress

薄膜力学性能的表征参数主要有硬度和弹性模量。依据图6结合XRD图可知，Ti薄膜并没有随厚度的变化出现相结构的变化，故其硬度和弹性模量值的变化不明显。Ti薄膜的硬度和弹性模量总体变化趋势一致，为先减小，薄膜厚度为1200nm时，弹性模量与硬度值最小，随后增大，厚度为2400nm时，弹性模量和硬度值最大，薄膜厚度为3600nm时Ti薄膜的硬度和弹性模量值又出现减小现象。

表1为电子薄膜应力分布测试仪测量结果，从表中可以看出薄膜内部应力随薄膜厚度的增加先增大后减小，厚度为3600nm时薄膜存在残余压应力，其数值为最小值，当薄膜厚度为1200nm时，薄膜内部残余应力转变为残余拉应力，并在薄膜中分布最为均匀，而薄膜厚度为2400nm时，应力在薄膜内变化差异最大。结合电子薄膜应力分布测试仪测量结果，发现薄膜中存在压应力时，薄膜的硬度和弹性模量较大，拉应力存在时则较小。薄膜中残余拉应力增大会使其硬度和弹性模量值减小，这与Suresh等[27]用铝合金8009实验所得结果一致。

图6 不同厚度Ti薄膜的硬度和弹性模量 (a)硬度;(b)弹性模量Fig.6 Hardness and elastic modulus at different thicknesses of Ti film (a)hardness;(b)elastic modulus

表1 不同厚度Ti薄膜残余应力分布表

3 结论

(1)运用直流磁控溅射方法制备出的Ti薄膜表面光滑，结构致密。随着薄膜厚度的增加，薄膜晶粒逐渐增大，其中薄膜厚度为1200nm时，Ti薄膜表面最为均匀，粗糙度也较小。

(2)Ti薄膜表面在一定尺度范围内存在良好的分形特性。在此区间内，分形维数能够较好地表征薄膜三维形貌特征。薄膜表面的粗糙度随着薄膜厚度的增加先增大后减小，薄膜厚度为1200nm时最小，2400nm时最大，分形维数与粗糙度变化结合可以对薄膜表面形貌做出更好的分析。

(3)随Ti薄膜厚度的增加，Ti薄膜内部应力先增大后减小，薄膜厚度为3600nm时，残余应力最小，表现为残余压应力，薄膜厚度为1200nm时，残余应力最大，为残余拉应力；结合电子薄膜应力分布测试仪测试结果和纳米压痕结果分析得出：薄膜中存在拉应力时，残余应力在Ti薄膜内部分布较为均匀，此时Ti薄膜具有较强的抵抗外加载荷的能力，并且塑性变形较小，但薄膜中存在残余拉应力会使薄膜硬度和弹性模量有所减小。

[1] DUMONT E, DUGNOILLE B, PEITJEAN J P, et al. Optical properties of nickel thin films deposited by electroless plating[J]. Thin Solid Films, 1997, 301(1): 149-153.

[2] 夏冬生, 张会臣, 孙昌国, 等. 离子束增强沉积Ni, Ti 纳米金属薄膜的表面形貌与摩擦特性研究[J]. 润滑与密封, 2007, 32(4): 97-101.

XIA Dong-sheng, ZHANG Hui-chen, SUN Chang-guo, et al. Study on topography and friction properties of nanometer metallic coatings[J]. Lubrication Engineering, 2007, 32(4): 97-101.

[3] NAPLOSEZK-BILNIK I, BUDNIOK A, LOSIEWICZ B, et al. Electrodeposition of composite Ni-based coatings with the addition of Ti or/and Al particles[J]. Thin Solid Films, 2005, 474(1): 146-153.

[4] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J]. Journal of Materials Research, 1992, 7(6): 1538-1564.

[5] OLIVER W C, PHARR G M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology[J]. Journal of Materials Research, 2004, 19(1): 3-20

[6] 王红美, 徐滨士, 马世宁，等. 纳米压痕法测试电刷镀镍镀层的硬度和弹性模量[J]. 机械工程学报, 2005, 41(4):128-131.

WANG Hong-mei, XU Bin-shi, MA Shi-ning, et al. Hardness and modulus of elasticity of brush plated nickle coating by nanoindentation testing[J]. Chinese Journal of Mechanical Engineering, 2005, 41(4):128-131.

[7] DOERNER M F, NIX W D. A method for interpreting the data from depth-sensing indentation instruments[J]. Journal of Materials Research, 1986, 1(4): 601-609.

[8] 吴化, 陈涛, 宋力. PVD 法制备 (Ti, Al) N 涂层中残余应力对其质量的影响[J]. 材料工程, 2013,(2): 60-64.

WU Hua, CHEN Tao, SONG Li. Effects of residual stress on quality of(Ti,Al)N coatings deposited by PVD method[J]. Journal of Materials Engineering, 2013, (2): 60-64.

[9] MORRIS M, WALDHEIM L. Energy recovery from solid waste fuels using advanced gasification technology[J]. Waste Management, 1998, 18(6): 557-564.

[10] 李远士, 牛焱, 吴维，等. Fe-Cr合金在450℃的KCl及KCl-ZnCl2盐膜中的腐蚀[J]. 金属学报, 2001, 37(9): 961-964.

LI Yuan-shi, NIU Yan, WU Wei, et al. Corrosion behaviors of Fe-Cr alloys induced by KCl and KCl-ZnCl2at 450℃[J]. Acta Metallurgica Sinica, 2001, 37(9): 961-964.

[11] 王成, 张贵彦, 马莹, 等. 薄膜应力测量方法研究[J]. 激光与光电子学进展, 2005, 41(9): 28-32.

WANG Cheng, ZHANG Gui-yan, MA Ying, et al. Study of thin film stress measurements[J]. Laser and Optoelectronics Progress, 2005, 41(9):28-32.

[12] STARMAN L, COUTU J R. Stress monitoring of post-processed MEMS silicon microbridge structures using Raman spectroscopy[J]. Experimental Mechanics, 2012, 52(9): 1341-1353.

[13] 王海斗，朱丽娜，邢志国. 表面残余应力检测技术[M]. 北京:机械工业出版社, 2013. 31-53.

WANG Hai-dou, ZHU Li-na, XING Zhi-guo. The Technology of Surface Residual Stress Testing [M]. Beijing: China Machine Press, 2013. 31-53.

[14] 胡望宇, 管恒荣, 孙晓峰,等. ZrO2-Ni等离子喷涂涂层的残余应力[J]. 材料工程, 1999, (2): 3-5.

HU Wang-yu, GUAN Heng-rong, SUN Xiao-feng, et al. Residual stress of ZrO2-Ni coatings prepared by plasma spraying[J]. Journal of Materials Engineering, 1999, (2): 3-5.

[15] SERGEJEV F, KIMMARI E, VILIUS M. Residual stresses in TiC-based cermets measured by indentation[J]. Physics Engineering, 2011, 10: 2873-2881.

[16] 毛卫国, 陈强, 张斌, 等. 等离子喷涂热障涂层材料弹性模量与硬度的压痕测试分析[J].材料工程,2011, (10): 66-71.

MAO Wei-guo, CHEN Qiang, ZHANG Bin, et al. Investigations of elastic modulus and hardness of air plasma sprayed thermal barrier coatings by nanoindentation method[J]. Journal of Materials Engineering, 2011,(10): 66-71.

[17] 张泰华. 微/纳米力学性能测试技术及其应用[M]. 北京:机械工业出版社, 2005.21-23.

ZHANG Tai-hua.The Technology of Micro/Nano Mechanical Properties Testing and its Application [M]. Beijing: China Machine Press, 2005.21-23.

[18] 曹猛, 李强, 杨莹,等. 离子束流和基底温度对 ZrN/TiAlN 纳米多层膜性能的影响[J]. 真空科学与技术学报, 2008, 28(增刊1): 29-32.

CAO Meng, LI Qing, YANG Ying, et al. Deposition conditions and mechanical properties of ZrN/TiA1N nanoscaled multilayered coatings[J]. Chinese Journal of Vacuum Science and Technology, 2008, 28(Suppl 1): 29-32.

[19] ABDUL KHADAR M, MOHEMMED SHANID N A. Nanoscale fine-structure evaluation of RF magnetron sputtered anatase films using HRTEM, AFM, micro-Raman spectroscopy and fractal analysis[J]. Surface and Coatings Technology, 2010, 204(9): 1366-1374.

[20] GUESSASMA S, MONTAVON G, CODDET C. On the implementation of the fractal concept to quantify thermal spray deposit surface characteristics[J]. Surface and Coatings Technology, 2003, 173(1): 24-38.

[21] RIVETT B, KOROLEVA E V, GARCIA-GARCUA F J, et al. Surface topography evolution through production of aluminium offset lithographic plates[J]. Wear, 2011, 270(3): 204-217.

[22] CHEN X H, WANG D W. Fractal and spectral analysis of aggregate surface profile in polishing process[J]. Wear, 2011, 271(11): 2746-2750.

[23] TANG W, WANG Y. Fractal characterization of impact fracture surface of steel[J]. Applied Surface Science, 2012, 258(10): 4777-4781.

[24] ZHANG X C, XU B S, WU Y X, et al. Porosity, mechanical properties, residual stresses of supersonic plasma-sprayed Ni-based alloy coatings prepared at different powder feed rates[J]. Applied Surface Science, 2008, 254(13): 3879-3889.

[25] KWASNY W, DOBRZANSKI L A, PAWLYTA M, et al. Fractal nature of surface topography and physical properties of the coatings obtained using magnetron sputtering[J]. Journal of Materials Processing Technology, 2004, 157: 188-193.

[26] WANG Y, XU K W. Cu-W thin film characterized by surface fractal and resistivity[J]. Acta Physica Sinica, 2004, 53(3): 900-904.

[27] SURESH S, GIANNAKOPOULS A E. A new method for estimating residual stresses by instrumented sharp indentation[J]. Acta Materialia, 1998, 46(16): 5755-5767.

Mechanical Properties of Nano Ti Films with Different Thickness

WANG Hai-dou1,DONG Mei-ling1,2,CUI Xiu-fang2,XING Zhi-guo1,ZHU Li-na3,LIU Jin-na1,2

(1 National Key Laboratory for Remanufacturing，Academy of Armored Forces Engineering，Beijing 100072，China; 2 School of Materials Science and Chemical Engineering,Harbin Engineering University,Harbin 150001，China; 3 School of Engineering and Technology,China University of Geosciences,Beijing 100083，China)

Four nano-Ti films with different thickness were deposited by direct current magnetron sputtering (DCMS). The mechanical properties and residual stress of the deposited Ti films were studied using nano indentation and electronic film stress distribution tester, surface roughness and surface morphology were analyzed using fractal dimension and the atomic force microscopy (AFM) respectively. The results show that, with the increase of the film thickness, the Ti crystal grain size increases gradually and both the surface roughness and residual stress increase first and then decrease, while the hardness and elastic modulus exhibit the opposite tendency. When the thickness of the deposited films is 600, 2400nm and 3600nm, the residual compressive stress exists; when the film thickness is 1200nm, the residual tensile stress exists, the distribution of residual stress is most uniform, when the residual tensile stress exists in the thin films, but the hardness and elastic modulus are lower. The analysis shows that residual tensile stress results in the decrease of the hardness and elastic modulus in Ti thin films, the residual compressive stress exhibits an opposite trend.

film;nanoindentation;fractal dimension;mechanical property

10.11868/j.issn.1001-4381.2015.11.009

TG133.25

A

1001-4381(2015)11-0050-07

北京市自然科学基金重大项目(3120001)；国家自然科学基金(51275105)；国家杰出青年科学基金(51125023)

2014-04-17；

2014-12-10

王海斗(1969—)，男，教授，从事表面工程、再制造的寿命预测等研究，联系地址：北京市丰台区杜家坎21号装甲兵工程学院(100072)，E-mail: wanghaidou@aliyun.com