加强类比教学，注重关联拓展——以“等边三角形”教学为例

☉江苏省如东县岔河中学 杨小红

加强类比教学，注重关联拓展
——以“等边三角形”教学为例

☉江苏省如东县岔河中学 杨小红

不同版本的教材中，等边三角形通常被安排在等腰三角形之后，学生自主探究并证明等边三角形的性质与判定，从而得出一些“升级”之后用“黑体字”定理，再例题讲评、习题训练.这样的教学安排固然倡导了学生研究新知的自主性，然而从贴近学生“最近发展区”，基于数学前后一致、逻辑连贯的高度来看，等边三角形教学应该有很多值得研讨的空间.本文呈现最近笔者开设的一节等边三角形的教学设计，并阐释相关教学立意.

一、“等边三角形”教学设计

（一）教学目标

（1）从等腰三角形出发，特殊化后研究并概括等边三角形的性质与判定；

（2）利用等边三角形的性质与判定解决问题，应用新知简化推理证明；

（3）将等边三角形“取半”研究含30°的直角三角形的性质，并“反过来”思考它的逆命题，传递数学研究的方法.

（二）重点和难点

重点是学生自主探究并概括等边三角形的性质和判定；难点是灵活应用新知简化推理证明.

（三）教学流程

1.开课引入

如图1，

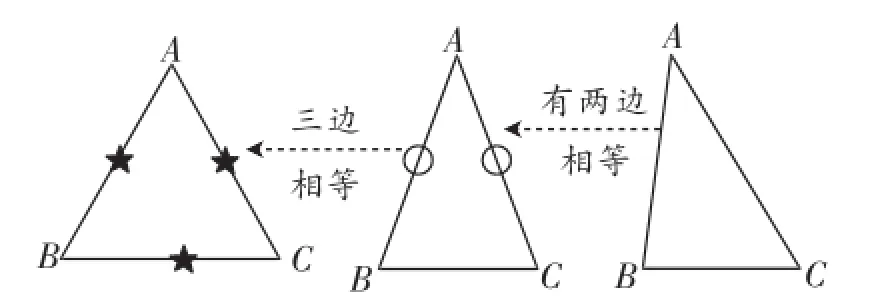
图1

从一般三角形出发，不断添加强化条件，先增加有两边相等的三角形，为前面刚学的等腰三角形，继续特殊化，当三边都相等时，得到等边三角形.板书本课的课题：等边三角形.

再板书等边三角形的定义：三边相等的三角形称为等边三角形.

2.新知探索

问题1：等边三角形有哪些性质呢？

问题2：如何判定一个三角形为等边三角形？

预设意图：引导学生回顾等腰三角形的研究套路：定义→性质→判定→应用.按此“套路”学生自主研究等边三角形.学生自主探索之后，小组内交流，最后大组内汇报展示，教师按“套路”板书（见后面“板书设计”）.比如概括等边三角形的性质时，可以从边、角、重要线段、对称性等角度来展开；等边三角形的判定可以从边、角、一个角为60°的等腰三角形等角度展开.需要指出的是，考虑到教学时间和学生已有的全等证明经验，关于等边三角形的性质或判定的证明过程以教师追问学生依据为主，不安排书面书写证明过程，这不是本课的重点.

3.例题教学

例题如图2，△ABC是等边三角形，DE//BC，分别交AB、AC于点D、E.求证：△ADE是等边三角形.

图2

教学预设：本题证明方法很多，可以从边、角、等腰三角形等角度出发，寻找强化出来的条件证明等边三角形，教师通过追问不同学生的理解、多解证明的展示巩固等边三角形的性质与判定.

例题变式：如图3，△ABC是等边三角形，点D在BA的延长线上，作DE//BC，交AC的延长线于点E.求证：△ADE是等边三角形.

图3

教学预设：通过变式，让学生从点在边AB上，到在直线AB上，传递从特殊到一般的研究意识.

4.拓展研究

继续回到等边三角形，如图4，作出等边三角形ABC的一条角平分线AD后，由“三线合一”得出直角三角形ABD，抽离出图5，引导学生标注出图5中的锐角∠A的度数，并设计问题.

提问：图5中，BD、AB有怎样的数量关系？（AB＝2BD）如何证明？（补成图4这样的等边三角形即可，安排学生讲解思路）

变式：“反过来”思考，如图6，在Rt△ABD中，∠D＝90°，且AB＝2BD，能否求出∠A的度数呢？（预设：学生延长BD到C，使BC＝BA，既补全图形得到图4，然而此时证明△ABC是等边三角形方法是有区别的，先安排学生独立思考，写出证明过程，并安排学生板演证明过程，以备教师点评）

图5

图6

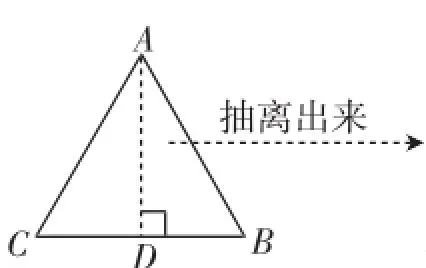
图4

5.小结

小结问题1：本课研究等边三角形时，主要是从哪些角度来概括的？你有怎样的研究心得与其他同学分享呢？（比如，学生可以从板书中讲述等边三角形研究的套路）

小结问题2：一幅三角板中没有用等边三角形，却用了两个直角三角形，你觉得这是什么原因？（一幅三角板中的两个直角三角形分别含有30°、45°，它们分别可以拼成等边三角形、正方形，让学生感受工具的“求简”追求）

6.布置作业

原创题：如图7，D、E分别为等边△ABC的边BC、AC上的动点，且BD＝CE，连接BE、AD交于点F.

图7

（1）求证：△ABD≌△BCE；

（2）求∠BFD的度数；

（3）作AH⊥BE于点H，求证：AF＝2FH；

（4）小凡练习以上问题后，提出一种变式拓展的思考，当点D、E分别在CB、AC的延长线上时，直线BE、AD相交于点F，其余条件不变，请画出符合要求的图形，猜想AF与FH的数量关系，并说明理由.

设计意图：求出∠AFE为60°是关键，可得出∠FAH为30°，从而得出含30°的直角三角形.最后一问虚拟学生变式拓展的思考，意图启发学生学会探究，渗透从特殊到一般的探索方法.

（四）板书设计

等边三角形

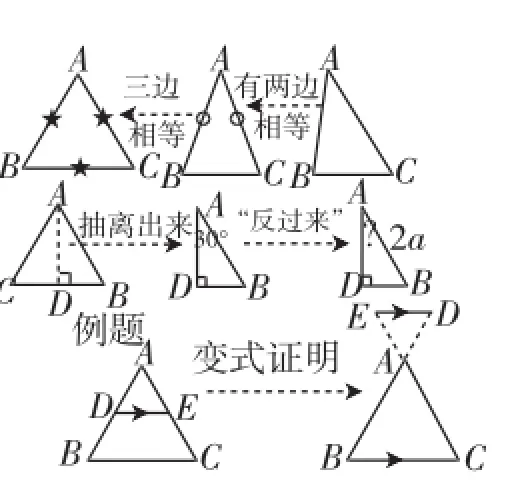
二、教学立意的进一步阐释

1.加强类比教学，渗透数学研究的“套路意识”

数学训练很多数学思想方法，其中类比就是一种重要的思想方法.日本数学家米山国藏所指出的：数学是一步一步向上走.很多数学新知识、新概念的研究，常常要借助于之前所学知识的基础、方法、研究思路来继续新的发现探索，这时注意向学生渗透研究问题的套路意识就显得十分重要.如本课中，注意引导学生借助在等腰三角形学习过程中积累的研究套路：“定义→性质→判定→应用”，学生可以按此进行自主探索、归纳概括，再小组交流、全班展示，追求对话教学的真实互动.

2.注重关联拓展，将数学课堂“向四面八方打开”

《义务教育数学课程标准（2011年版）》关于“课程目标”下“总目标”第2点即指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系……”.美国国家数学委员会（National Mathematics Advisory Panel）的成员伍鸿熙教授指出，“数学是连贯的；它是一张编织紧密的挂毯，其中所有概念和技巧逻辑严密地编织在一起，形成一个统一的整体.”然而就我们在日常教学观摩中所见，很多例题、习题的设计常常是较低层次的关联、链接，且多属于拼凑式的习题单式的学案类型.正是认识到上述不足，我们预设一道例题并变式，本课的作业也是一道与例题类似的原创题，而在拓展研究中从等边三角形抽离出一个含30度的直角三角形，并引导学生“反过来”研究其逆命题，这些努力都是向学生传递“特殊与一般”之间的关系，让学生感受到数学习题的变式拓展的一些可能.想来，如果能长此以往，我们的数学课堂应该就是学者所指出的“向四面八方打开”的开放教学吧.

1.【日】米山国藏，著.数学的精神、思想和方法［M］.毛正中，吴素华，译.成都：四川教育出版社，1986.

2.曹一鸣.为改进数学教育而共同努力——第12届国际数学教育大会综述［J］.人民教育，2012（17）.

3.杨九俊.学科育德不只在说教中［J］.中国德育，2011（11）.

4.李庾南，陈育彬.中学数学新课程教学设计30例［M］.北京：人民教育出版社，2007.

5.张恭庆.数学的有机统一是数学科学固有的特点［J］.高等数学研究，2011（9）.

6.刘东升.关联性：一个值得重视的研究领域［J］.中学数学（下），2013（12）.Z