SARIMA模型在戊型肝炎发病趋势预警预测中的应用
祝寒松,黄文龙,谢忠杭,陈光敏,曹 洋,章灿明,陈 武,欧剑鸣,洪荣涛
SARIMA模型在戊型肝炎发病趋势预警预测中的应用
祝寒松1,黄文龙1,谢忠杭1,陈光敏1,曹 洋2,章灿明1,陈 武1,欧剑鸣1,洪荣涛1
目的 采用SARIMA模型对福建省戊肝发病趋势进行预测,为预警和风险评估提供定量数据。方法 以Eviews5.0对福建省2004年1月-2015年12月戊肝的月发病例数进行SARIMA分析。结果 2004年1月-2014年8月福建省戊肝月发病序列呈先升后降的趋势和周期性波动,取自然对数和1次1阶非季节差分后序列得到平稳化,模型SARIMA (0,1,1)(1,0,1)12和SARIMA(2,1,0)(1,0,1)12参数有统计学意义,残差为白噪声,后者为最优模型,表达式为:(1+0.61L+0.23L2)(1-0.89L12)(1-L)log(yt)=(1-0.89L12)εt。静态回代预测值和实际值吻合较好,相对误差取绝对值后均数为13.06%。2014年1-8月预测值的相对误差较小(5月份除外),预测标准误(S.E)较小。结论 运用SARIMA模型可对戊肝发病趋势进行较准确的短期预测,可为及时、科学地研判风险提供可靠的数据基础。
季节时间序列模型;戊肝;预警;预测;风险评估
戊型肝炎(戊肝,Hepatitiv E)是由戊型肝炎病毒引起的一种急性人兽共患病,目前在全球各地广泛传播,严重危害人类健康,据估计20亿的世界人口有可能被感染Hepatitiv E病毒的风险,死亡率也占0.5%,并且有可能在许多发展中国家导致大暴发,近年来发病率在我国呈逐年上升趋势[1-3]。为了对戊肝发病趋势进行预测和预警,考虑到其发病具有一定的周期性,而季节时间序列模型(Seasonal Autoregressive Integrated Moving Average Model, SARIMA)可用于对存在周期性变化的时间序列进行预测,因此,本文拟采用SARIMA模型对福建省戊肝发病趋势进行定量预测,以期为风险评估提供基础资料,现报告如下。
1 材料与方法
1.1 材料 来自福建省各级卫生机构通过中国疾病预防控制信息系统的报告(按“现住址”、“终审”选项下载)。
1.2 方法 采用SAS9.2软件对数据进行汇总、清洗,运用Eviews 5.0软件对数据进行SARIMA建模和分析,α=0.05(双侧)。
1.2.1 原理 ARIMA模型通常借助时间序列的随机特性来描述事物的发展变化规律,从而解释并预测时间序列的变化发展规律,而SARIMA模型是ARIMA模型的扩展和改进,包含了季节性或周期性因素[4-5],对于存在季节性的非平稳时间序列不能直接建立ARIMA模型,可考虑进行非季节差分和季节性差分使其平稳化,基本模型:SARIMA(p,d,q)(P,D,Q)S,表达式为:φp(L)ΦP(LS)(1-L)d(1-LS)Dyt=θq(L)ΘQ(LS)εt。其中,p、q分别是非季节自回归过程AR和移动平均过程MA的阶数;d、D分别是序列yt的非季节差分和季节差分阶数;P、Q分别是季节自回归过程SAR和移动平均过程SMA的阶数。φp(L)、ΦP(L)分别是非季节自回归过程AR和季节自回归过程SAR的滞后算子多项式,θq(L)、ΘQ(LS)分别是非季节移动平均过程MA和季节移动平均过程SMA的滞后算子多项式,(1-L)d、(1-LS)D分别是对序列yt的非季节差分和季节差分滞后算子,S是季节差分的步长,εt是残差序列(白噪声序列)。
1.2.2方法 ①绘制原序列的曲线图以识别其基本形式,加入截距项和时间趋势项做ADF单位根检验和Q统计量以判断平稳性。若为非平稳,可考虑对其取自然对数后做非季节差分和(或)季节性差分使之满足平稳性条件。②识别新序列自相关函数(autocorrelation function, ACF)和偏相关函数(partial autocorrelation function, PACF) 的SARIMA模型形式。③估计模型参数,对结果进行t检验(参数检验),通过Q检验进行残差分析(白噪声检验)。如果残差序列不是白噪声序列,说明残差序列中还存在有用的信息未被提取出来,需要对原模型进一步调整,以便得到更合适的模型。④利用调整R2、Akaike info criterion (AIC)准则和Schwarz criterion (SC)准则评价其相对优势,调整R2越大、AIC和SC越小,一般认为越好。⑤利用所估计的SARIMA模型,进行回代评价和预测。
2 结 果
2.1 原序列分析 2004年1月-2014年8月福建省戊肝月发病序列呈先升后降的趋势和周期性波动(图1),ADF单位根检验,P=0.00<0.05,但自相关函数呈现指数衰减,且衰减速度缓慢,所以认为该序列不平稳(图2)。
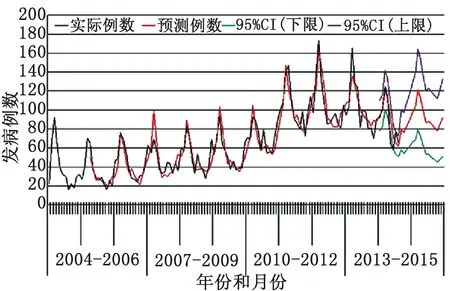
图1 福建省2004-2015年戊肝月发病例数的实际值和预测值
Fig.1 Observed and predicted values of hepatitis E in Fujian Province, per month from 2004 to 2015

图2 福建省2004年1月-2014年8月戊肝月发病数序列的自相关和偏相关图
Fig.2 ACF and PACF diagram of hepatitis E incidence in Fujian Province, per month from January 2004 to August 2014
2.2 平稳化 采用2种方法对原序列进行处理,第1种是取自然对数和1次1阶非季节差分,再做1次12阶季节差分;第2种是只取自然对数和1次1阶非季节差分。通过比较,后者效果更好,现只对其进行分析:差分后的序列已接近平稳(图3),ADF单位根检验P=0.00<0.05;ACF和PACF显示,序列平稳性已得到明显改进,滞后1阶和7阶显著地不为0,其它近似为1个平稳过程(图4)。因此,可认为序列已得到平稳化。

图3 经自然对数和1次1阶非季节差分后的序列
Fig.3 Time series diagram after conducting natural logarithm and once non-seasonal of lag 1 difference
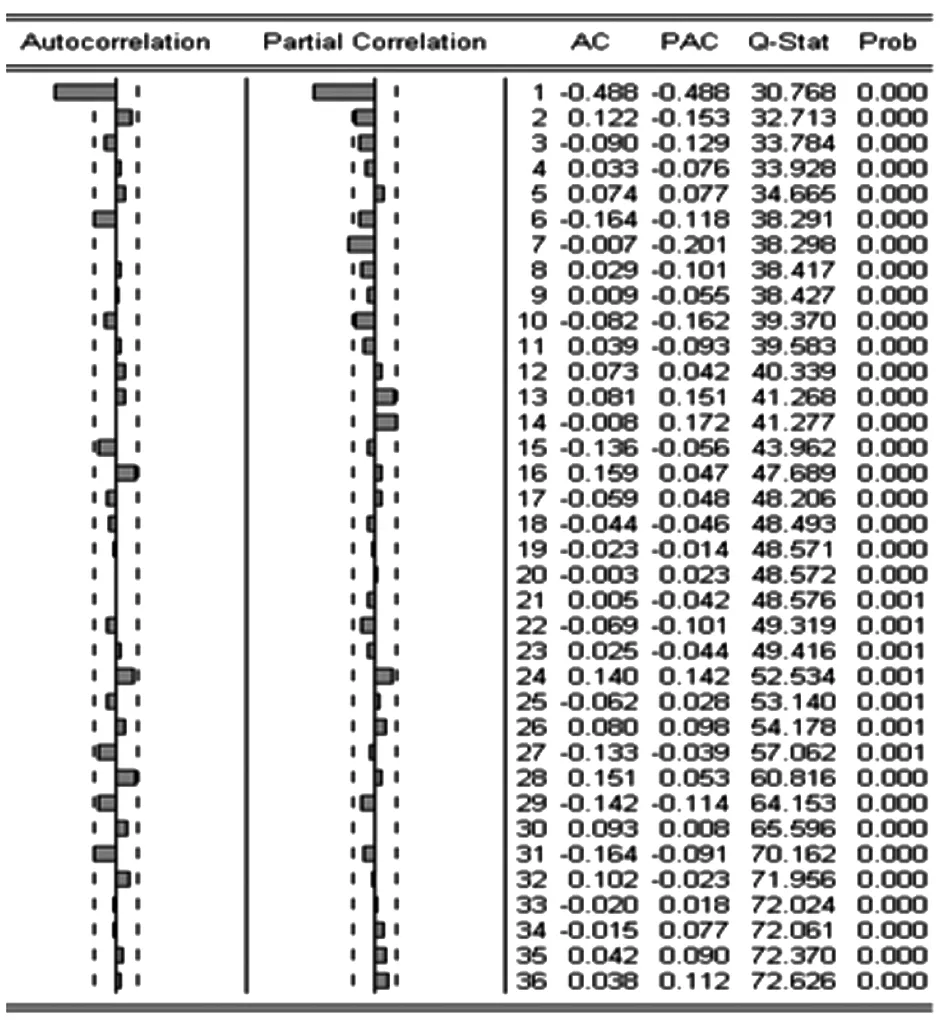
图4 序列经差分后的自相关和偏相关图
Fig.4 ACF and PACF diagram after conducting natural logarithm and a non-seasonal difference
2.3 建模 由2.2差分可知d=1、D=0,ACF滞后1阶呈截尾,PACF滞后2阶呈截尾或者拖尾至2阶。通过尝试,2组模型通过t检验(p<0.05)和Q检验(全部p>0.05,已呈明显的白噪声序列):SARIMA(0,1,1)(1,0,1)12、SARIMA(2,1,0) (1,0,1)12(表1)。通过调整R2、AIC和SC比较,SARIMA(2,1,0) (1,0,1)12拟合优度较好(表2),Q检验见图5,表达式为:(1+0.61L+0.23L2)(1-0.89L12)(1-L)log(yt)=(1-0.89L12)εt。

图5 SARIMA(2,1,0)(1,0,1)12模型的Q检验
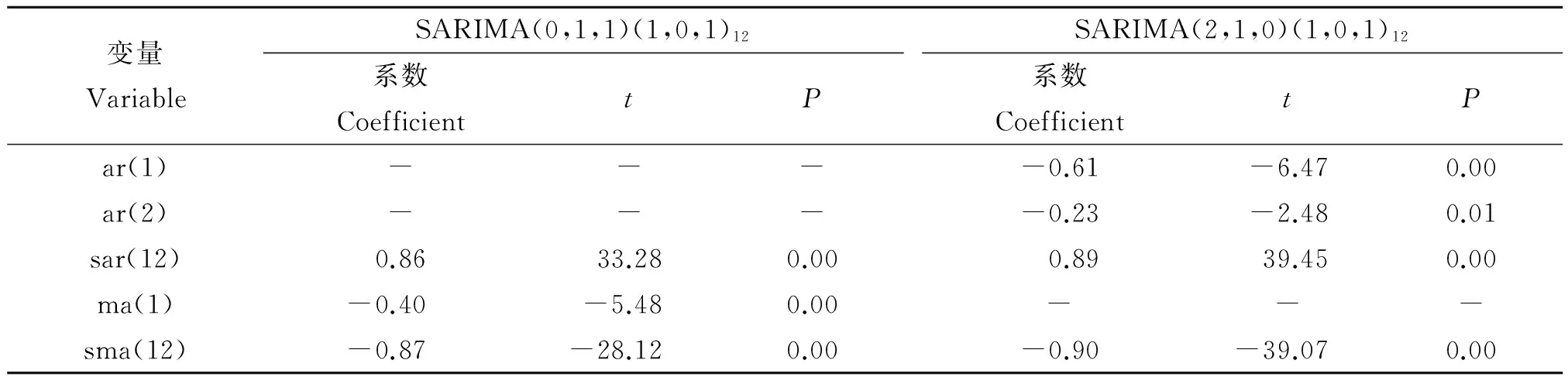
变量VariableSARIMA(0,1,1)(1,0,1)12系数CoefficienttPSARIMA(2,1,0)(1,0,1)12系数CoefficienttPar(1)----0.61-6.470.00ar(2)----0.23-2.480.01sar(12)0.8633.280.000.8939.450.00ma(1)-0.40-5.480.00---sma(12)-0.87-28.120.00-0.90-39.070.00

表2 2组SARIMA模型的拟合优度比较
2.4 预测 采用SARIMA(2,1,0)(1,0,1)12模型回代静态预测评估,拟合结果显示,预测值和实际值吻合较好,2004年1月-2005年3月的实际值经差分已去除(图1),2005年4月-2014年8月相对误差均数为0.34%,取绝对值后相对误差均数为13.06%。2014年1-8月预测值的相对误差较小(5月份除外),预测标准误(S.E)较小(表3)。2014年9月-2015年12月进行动态预测,S.E逐渐较大(图1),2014年9-12月的S.E和95%CI上下限见表3。
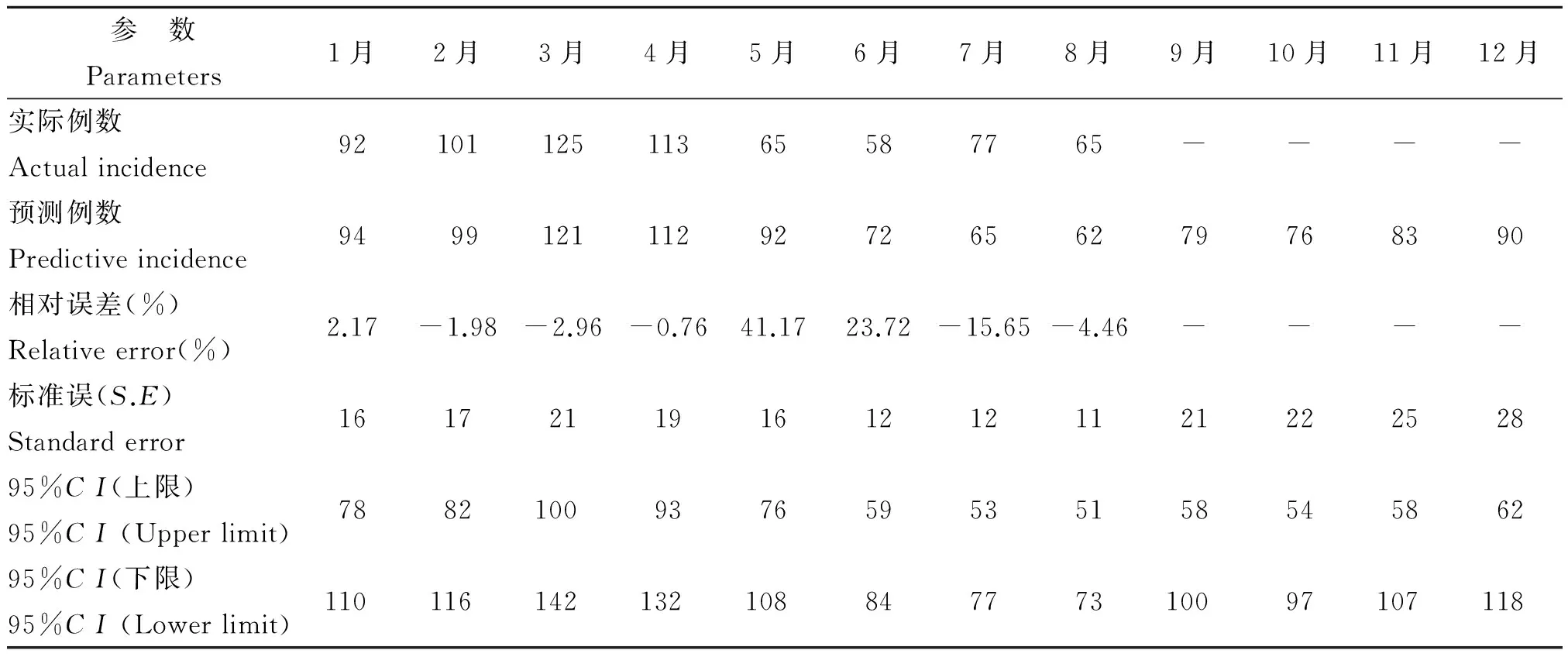
表3 福建省2014年戊肝预测情况
3 讨 论
戊肝传播途径多样,其中以粪-口途径传播为主,而且有证据显示通过摄食受感染的肉类可以引起人兽共患传播,易引起食物或水源性流行暴发,另外,普通人群戊肝病毒的感染率较高,提示亚临床感染的存在,也是无症状感染、重症肝炎、不明原因肝炎以及暴发性急性肝炎的重要原因之一[6-7],然而,目前该病尚缺乏特效的治疗方法,也没有特异性免疫制剂可供预防,而福建省省戊肝发病总体呈上升态势。因此,加强戊肝监测资料分析并予以预测预警以严防流行和暴发显得尤为重要。
但传染病的暴发流行受到多种不确定因素的影响,这使得在传染病早期的预测预警上存在着诸多困难,导致了传染病早期预防控制工作一直较为滞后,因此如何及时有效地预测预警传染病的暴发流行一直是传染病预测控制工作的重点[8-10]。
应用模型对传染病的发病及流行强度进行预测预警有多种方法:灰色动态模型GM(1,1)将原始序列累加、求均值而生成新的数列,使得GM(1,1)模型预测精度降低;利用人工神经网络(ANN)模型预测发病率,其难度在于确定网络结构,隐含层节点数太少,预测精度无法保证,节点数太多,又易陷入局部极小值,因此如何选择一个最佳的网络结构,成为一个关键问题;传统的时间序列模型要求序列具有平稳的线性趋势,但许多传染病的发病情况有着明显的季节性和周期性,如果不考虑这些因素的影响,做出的预测往往不精确[11-12]。而SARIMA模型适用于多种复杂的时间序列模式,可将拟合误差作为重要因素纳入模型中,因此预测精度较高,作为疾病风险评估、预防和控制的监测数据,这对于规划公共卫生干预措施是一个非常有价值的工具[13-14]。
福建省戊肝月发病序列总体呈现明显的周期性波动(图1),而且自相关函数呈指数缓慢衰减,为非平稳性,因此该序列比较适合建立SARIMA模型定量预测月(周)发病数(率),可以为传染病风险评估提供基础数据。
分析显示,SARIMA(2,1,0)(1,0,1)12模型拟合效果较好,回代预测值和实际值相当吻合(平均误差为13.06%),对2014年的预测标准误较低,表明该模型预测较为准确、精度较高,可以认为它对于原序列是个理想的模型。但是也要注意到,图1中紫色和绿色间的2014-2015年预测置信区间逐渐变宽,从而表明预测期越往后,模型的预测精度越差,因此比较适用于短期预测。在实际应用中,应该不断加入新的实际值,然后修正模型和重新拟合预测值[15],所以对于2015年,在2014年的实际值纳入序列矫正之后再做以预测,结果才能更可靠。
值得一提的是,除5月份外,2014年1-8月的相对误差较小,是较为成功的模型预测。至于5月份,其实际值偏低,且低于预测值的95%CI下限,同时大幅低于2011-2013年同期实际值(113、104和124例),需要从网络直报、自然环境因素和防控力度的加强等多方面因素考虑。另外,本研究显示,2014年2-4月和7、8月实际值均不高于95%CI上限预警值,实际情况也无流行和暴发,与预测基本一致。
但也应注意到,由于SARIMA模型也有不足之处,一是建立合理的模型需要大量的观测数据(至少50个样本);二是该模型是基于正态假设,对于罕见病,即便是对数或平方根转换后也不是十分合适。所以对于小样本,可以结合泊松回归模型预测,但对于大样本,前者的预测精确度高于后者[16]。
[1]Lin J, Norder H, Uhlhorn H, et al. Novel hepatitis E like virus found in Swedish moose[J]. J Gen Virol, 2014, 95(Pt 3): 557-570. DOI: 10.1099/vir.0.059238-0
[2]Kuniholm MH, Purcell RH, Mc Quillan GM, et al. Epidemiology of hepatitis E virus in the United States: results from the Third National Health and Nutrition Examination Survey, 1988-1994[J]. J Infect Dis, 2009, 200(1): 48-56. DOI: 10.1086/599319
[3]Wei S, Lu YH, Gao MY, et al. Time series analysis of hepatitis E incidence in China[J]. Chin J Health Statistics, 2012, 29(6): 808-811. (in Chinese) 魏珊, 陆一涵, 高眉扬, 等. 我国戊型肝炎发病例数的时间序列分析[J]. 中国卫生统计, 2012, 29(6): 808-811.
[4]Moosazadeh M, Nasehi M, Bahrampour A, et al. Forecasting tuberculosis incidence in Iran using Box-Jenkins models[J]. Iran Red Crescent Med J, 2014, 16(5): 1-6. DOI: 10.5812/ircmj.11779
[5]Kam HJ, Sung JO, Park RW. Prediction of daily patient numbers for a regional emergency medical center using time series analysis[J]. Healthc Inform Res, 2010, 16(3): 158-165. DOI: 10.4258/hir.2010.16.3.158
[6]Wang HR, Yan YS, Xiao JX, et al. Seroepidemiological investigation and analysis of hepatitis virus infection among various groups of population in Fujian province[J]. Chin J Zoonoses, 2007, 23(4): 370-372. (in Chinese) 王惠榕, 严延生, 萧剑雄, 等. 福建省不同人群中戊型肝炎病毒感染的血清流行病学调查分析[J]. 中国人兽共患病学报, 2007, 23(4): 370-372
[7]Arends JE, Ghisetti V, Irving W, et al. Hepatitis E: An emerging infection in high income countries[J].J Clin Virol, 2014, 59(2): 81-88. DOI: 10.1016/j.jcv.2013.11.013
[8]Yang Z, Ye ZH, You AG, et al. Application of multiple seasonal ARIMA model in prediction of tuberculosis incidence[J]. Chin J Public Health, 2013, 29(4): 469-473. (in Chinese) 杨召, 叶中辉, 尤爱国, 等. 乘积季节ARIMA模型在结核病发病率预测中的应用[J]. 中国公共卫生, 2013, 29(4): 469-473.
[9]Song Q. On the weight convergence of Elman networks[J]. IEEE Trans Neural Netw, 2010, 21(3): 463-480. DOI: 10.1109/TNN.2009.2039226
[10]Lai SJ, Li ZJ, Jin LM, et al. Evaluation content and their indicators of early warning system for infectious disease outbreak[J]. Chin J Epidemiol, 2009, 30(6): 637-641. (in Chinese) 赖圣杰, 李中杰, 金连梅, 等. 传染病暴发早期预警系统评价内容及其指标[J]. 中华流行病学杂志, 2009, 30(6): 637-641.
[11]Bras AL, Gomes D, Filipe PA, et al. Trends, seasonality and forecasts of pulmonary tuberculosis in Portugal[J]. Int J Tuberc Lung Dis, 2014, 18(10): 1202-1210. DOI: 10.5588/ijtld.14.0158
[12]Shen TQ, Liu WD, Hu JL, et al. The application of x-11-ARIMA process in dysentery prediction[J]. Chin J Health Statistics, 2014, 31(3): 395-398. (in Chinese) 申铜倩, 刘文东, 胡建立, 等. X-11-ARIMA过程在痢疾疫情预测中的应用研究[J]. 中国卫生统计,2014, 31(3): 395-398.
[13]An SY, Zhao Z, Guo JQ, et al. Forecasting measles epidemic situation by applying the time series model in Liaoning Province[J]. Chin J Health Statistics, 2014, 31(5): 781-783. (in Chinese) 安淑一, 赵卓, 郭军巧, 等. 应用时间序列模型预测辽宁省麻疹疫情[J]. 中国卫生统计, 2014, 31(5): 781-783.
[14]Feng HF, Duan GC, Zhang RG, et al. Time series analysis of hand-foot-mouth disease hospitalization in Zhengzhou: establishment of forecasting models using climate variables as predictors[J]. PLoS One, 2014, 9(1): 1-10. DOI: 10.1371/journal.pone.0087916
[15]Mehdi K, Mehdi B, Heiazi SR. Combining seasonal ARIMA models with computational intelligence techniques for time series forecasting[J]. Soft Comput, 2012, 16(6): 1091-1105. DOI: 10.1007/s00500 -012-0805-9
[16]Hu WB, Tong SL, Mengersen K, et al. Weather variability and the incidence of cryptosporidiosis: comparison of time series poisson regression and SARIMA models[J]. Elsevier Inc, 2007, 17(9): 679-688. DOI: 10.1016/j.annepidem.2007.03.020
SARIMA model for incidence trend and prediction of hepatitis E
ZHU Han-song1,HUANG Wen-long1,XIE Zhong-hang,CHEN Guang-min,CAO Yang2,ZHANG Can-ming1,CHEN Wu1,OU Jian-ming1,HONG Rong-tao1
(1.FujianProvincialCenterforDiseaseControl&Prevention,Fuzhou350001,China;2.ChineseCenterforDiseaseControlandPrevention,Bejing102206,China)
We forecasted the incidence trends of hepatitis E in Fujian Province by SARIMA model, in order to provide quantitative data for early warning and risk assessment. The monthly cases of hepatitis E in Fujian Province from January 2004 to December 2015 were analyzed for SARIMA using Eviews 5.0 software. Results showed that monthly incidence sequences of hepatitis E in Fujian Province, from January 2004 to August 2014, showed a trend of increased and then decreased, as well as cyclical fluctuations. And it was into smoothed after done natural logarithm and once non-seasonal of lag 1 difference. SARIMA (0,1,1)(1,0,1)12and SARIMA(2,1,0) (1,0,1)12were statistically significant,and the residual was white noise, in which the latter was the optimal model, expressed as: (1+0.61L+0.23L2)(1-0.89L12)(1-L)log(yt)=(1- 0.89L12)εt. Static back generation forecast and actual values were in good agreement, in which the mean of relative error was 13.06% after taking the absolute value. Relative error of predictive value in 2014 January to August (except in May) was small, and the prediction standard error (S.E) small, too. Incidence trends of hepatitis E could short-term predicted through SARIMA model, thus it could provide reliable data base in order to judge the risk of infectious disease more timely and scientifically.
SARIMA; hepatitis E; warning; forecast; risk assessment
Horg Rong-tao, Email:hrt@fjcdc.com.cn
洪荣涛,Email:hrt@fjcdc.com.cn
1.福建省疾病预防控制中心,福建省人兽共患病研究重点实验室,福州 350001; 2.中国疾病预防控制中心,应急中心监测预警与风险评估办公室,北京 102206
10.3969/cjz.j.issn.1002-2694.2015.02.014
R373
A
1002-2694(2015)02-0158-05
2014-09-12;
2014-11-23


