梯形载荷下伴随破碎的散粒体系统动力学分析

洪 俊 张 镇 刘 俊 王立源

(1东南大学土木工程学院，南京210096)

(2东南大学江苏省工程力学分析重点实验室，南京210096)

散粒体是几何尺寸基本属于同一量级的颗粒集合体.散粒体广泛存在于自然界中，如沙堆、矿石、谷物等.散粒体是由大量颗粒组成的不连续系统，有许多区别于固体和流体的力学行为特性.从微观角度来说，散粒体和固体都是由固体颗粒组成，但是散粒体不能承受拉力，并且颗粒之间有复杂的相互作用;从宏观角度来说，散粒体和流体都具有流动性，但却能够承受较大的剪切力.同时，散粒体材料的不均匀及各向异性的特点，导致散粒体的力学性能更加复杂.散粒体系统动力学的研究对地震、滑坡、泥石流、发射装药发射安全性等工程领域有着重要的理论意义和应用价值[1].建立在非连续介质力学基础上的离散单元法是散粒体系统动力学仿真的有力工具[2].

在发射装药导致的发射安全性事故中，散粒体发射药床挤压碰撞，其中部分药粒的脆性破碎是导致发射安全性事故的根本原因[3].研究梯形载荷作用下的发射药床挤压碰撞问题对发射装药导致的发射安全性具有重要的价值.洪俊等[4]利用离散单元法对梯形载荷作用下的散粒体系统力学行为进行了有效的数值研究，但未涉及到破碎问题.姜世平等[5-6]对冲击载荷作用下散粒体系统破碎问题进行了数值研究.发射药床挤压碰撞问题本质上是一个伴随颗粒破碎现象的散粒体系统动力学问题.建立在传统连续介质力学基础上的有限元法、有限差分法适用于预测损伤和破坏的区域，但难以直接计算和模拟材料及结构发生破坏的整个过程，而建立在离散单元法基础上的弹簧-球单元破碎模型[7]能够描述单个脆性材料的破坏过程.文献[8]将模拟单个脆性材料颗粒破坏过程的弹簧-球单元破碎模型应用到散粒体系统中，成功模拟了发射药床在冲击载荷作用下的破碎过程.

本文在文献[4]的基础上，考虑脆性颗粒材料的破碎，对梯形载荷作用下的圆筒内的散粒体系统动力学问题进行研究，为发射装药发射安全性提供理论基础.首先介绍离散单元法基本原理和弹簧-球单元破碎模型，然后编制相应的计算程序，对梯形载荷作用下的圆筒内伴随破碎现象的散粒体系统进行动力学分析，获得了外部载荷和散粒体系统变形、破碎之间的关系.

1 离散单元法基本原理

离散单元法广泛应用于岩土工程中土颗粒的微观机理研究，是描述微观结构破坏过程的有力工具.离散单元法最初由Cundall[2]提出，是研究非连续性颗粒物质结构和运动规律的一种数值方法，与连续介质理论对于颗粒物质的描述不同，它不是建立在最小势能变分原理上，而是建立在基本的牛顿第二运动定律上.下面着重介绍离散单元法的基本原理中最关键的部分，即单元间的作用力理论，其他基本原理及运动方程见文献[2].

在相邻2个单元间存在着一种或多种作用力，根据不同的力学作用机理，作用力可分为弹塑性力、黏性力等.通常，这些力可用位移或者速度的函数来描述，相邻单元间的连接关系可用接触模型或链接模型描述.接触模型没有变形协调条件的限制，可用来求解大变形和非线性等非连续介质复杂动力学问题.在链接模型中，单元间相互链接，符合变形协调条件，通常用于连续介质问题的求解.从连续介质问题到非连续介质问题的求解，实质是相邻单元间的连接关系从链接模型到接触模型的转化.

本文中，每个颗粒被离散成很多球形单元的集合体，颗粒内部的相邻球形单元间关系符合链接模型，分属于不同颗粒的相邻球形单元符合接触模型，而颗粒在挤压或冲击作用下的破碎符合相邻球形单元间的连接关系从链接模型到接触模型的转化.

1.1 链接模型中的单元间作用力

每个颗粒被离散成球形单元后，颗粒内部相邻单元之间的连接关系为链接模型.图1为单元i和单元j之间的链接模型.单元之间的作用力采用力和位移之间的关系计算.在整体坐标系中，法向和切向定义如图2所示.法向方向nij定义为单元i中心指向单元j中心;在和法向方向垂直的切向平面内，切向矢量sij分解为切向矢量s1和s2，其中s1和坐标平面ox1x3平行，s2和坐标平面ox1x3垂直.

图1 链接模型

图2 法向切向关系

在t时刻，模型中的法向作用力Fn，ij(t)和切向作用力(Fs1，ij和 Fs2，ij)计算如下:

式中，Δun为法向位移增量;Δus1和 Δus2分别为切向s1和s2方向的位移增量;kn，ks1和ks2分别为法向和切向弹性系数.链接模型中，单元i和j之间可以承受拉力、压力和剪切力.将颗粒离散成等直径球单元组成的Hex分布形式，根据连续介质力学理论，外力做功等于内部应变能的增加，由此计算得到弹簧的弹性系数和材料的物性系数之间的关系[9].

1.2 接触模型中的单元作用力

在挤压和冲击过程中，颗粒发生破碎，部分相邻球单元之间的连接关系从链接转化为接触.同时，不同颗粒之间的相邻球单元初始时也可能为接触关系.单元之间真正接触需要满足球心之间的距离小于两球半径之和.当2个单元真正接触后，单元间的接触力可采用如图3所示的接触模型计算.

图3 接触模型

在t时刻，模型中法向和切向的方向规定见图2，法向和切向作用力可用下式计算:

式中，kjn，kjs1和kjs2分别为法向和切向弹性系数.在接触模型中，单元i和j之间仅能承受压力和剪切力.弹簧的弹性系数和材料的物性系数之间的关系通过Hertz接触理论计算获得[10].当切向接触力大于最大静摩擦力时，粒子间产生滑移.由库仑摩擦定律确定切向接触力在s1和s2方向上的分量[2].

2 弹簧-球单元破碎模型

如图4所示，将一个球形颗粒采用Hex构型离散为一系列等直径球单元，离散后，任何相临的2个球单元间由一个弹簧组联系.用颗粒的质量除以离散单元的个数获得每个单元的等效质量.离散后的模型外形和原球形颗粒不可能完全一致，在某些位置会存在缺陷，并稍小于原球形外轮廓，但随着球单元的增加，这种缺陷将没有本质影响.

图4 球形颗粒的离散模型

本文采用Mohr-Coulomb[7]破坏理论描述颗粒破坏过程.将单元之间的关系简化为状态1和状态2.状态1中，单元间的关系为链接，单元间能够承受压力、拉力及剪切力;状态2中，单元间的关系为接触，只能承受压力和剪切力.如单元之间初始关系为状态1，当拉力或剪切力达到破坏极限时，单元之间的关系从状态1转化为状态2;如单元之间初始关系为状态2，不管单元之间的作用力如何变化，单元之间的关系仍为状态2.

在外载荷的作用下，离散后的各个单元将产生运动，在运动过程中单元间产生相互作用力.当单元间的作用力超过弹簧的强度极限时，弹簧破坏，裂纹产生.多个裂纹的产生、汇集将导致颗粒破碎.

3 伴随破碎的散粒体系统动力学分析

根据上述理论，用C语言编制了相应的计算程序，采用OpenGL显示图形，对圆筒中的球形脆性颗粒材料组成的散粒体系统在梯形载荷作用下伴随部分颗粒破碎的现象进行了动力学分析.

采用基于 Monte Carlo方法的 Metropolis算法[11]，在圆筒内生成了密实散粒体系统，如图5(a)所示.采用弹簧-球单元破碎模型对密实结构中的所有颗粒进行离散，在重力作用下，离散后的散粒体系统自由运动，目的是增加整个系统的密实度，减少球单元离散的影响.假设散粒体系统由n个颗粒组成，每个颗粒离散成m个球形单元，则整个系统单元数为m×n.对于本身就由大量颗粒组成的散粒体系统，离散单元越多，计算量就越大，虽然采用了文献[8]的加速算法，但仍需要综合考虑离散单元数和计算时间的平衡，即精度和速度的平衡.经过多次试算，将每个球形颗粒离散成57个球单元，可兼顾精度和速度.离散后的散粒体系统密实结构如图5(b)所示.

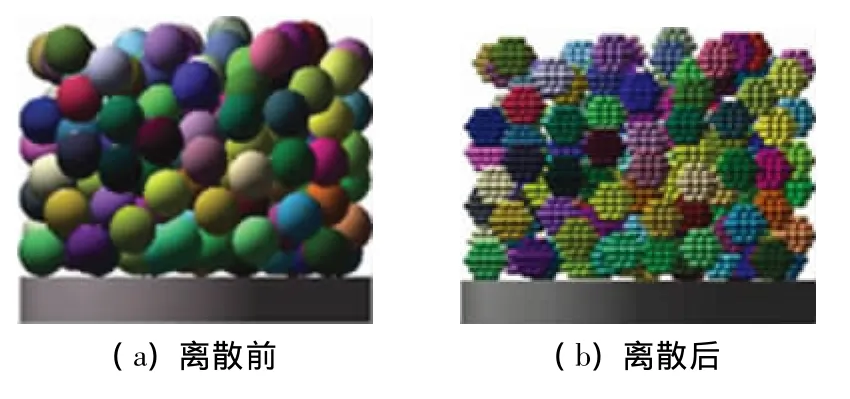
图5 散粒体系统密实结构

经过规则离散后的散粒体系统由大量球形单元组成，这些相邻球形单元之间存在着2种关系:接触关系或者链接关系.从链接关系到接触关系的转化采用弹簧-球单元破碎模型.任意时刻，每个单元的运动由离散单元法中的运动方程描述.

作用在活塞上的梯形载荷如图6所示.程序中输入参数包括初始条件、边界条件、材料参数及计算控制参数，见表1.初始条件为粒子及活塞的初始位置、速度等;边界条件包括活塞、圆柱底板及圆柱侧壁的参数;材料参数包括粒子的密度、弹性模量及泊松比等;计算控制参数包括时间步长、时间长度、载荷曲线、弹簧承载强度.

图6 活塞上的外部载荷

表1 计算参数

图7为计算过程中活塞的位移时间历程.结合图6和图7可看出:以圆筒下底面的上表面为0位置，从初始时刻到1 ms，活塞上的载荷大小为300 kN，由于活塞上的载荷小于散粒体系统的总承载能力，活塞处于0.545 38 m位置没有移动，散粒体系统处于初始稳定状态;从1 ms到3.2 ms，活塞上的载荷大小为500 kN，此时载荷大小大于散粒体系统的承载能力，活塞向下运动，当在2.5 ms时刻，散粒体系统被初步压实，承载能力达到500 kN，此时刻到3.2 ms，散粒体系统处于第2个稳定状态，活塞位置为 0.497 155 m;当从 3.2 ms到6.4 ms，活塞上的载荷大小为1 000 kN，此时载荷大于散粒体系统的承载能力，活塞向下运动，当在3.5 ms时刻，散粒体系统第2次被压实，承载能力达到1 000 kN，此时刻到6.4 ms，散粒体系统处于第3个稳定状态，活塞位置为0.485 854 m;当从6.4 ms到最终时刻8 ms，活塞上的载荷大小为1 500 kN，此时载荷大于散粒体系统的承载能力，活塞向下运动，当在6.6 ms时刻，散粒体系统第3次被压实，承载能力达到1 500 kN，此时刻到最终时刻8 ms，散粒体系统处于第4个稳定状态，活塞位置为0.475 751 m.散粒体系统达到第2，3，4个稳定状态所需时间分别为1.5，0.3 和0.2 ms，活塞的位移分别为0.048 225，0.011 301，0.010 103 m.

图7 活塞的位移时间历程

由以上分析可看出，在梯形载荷作用下，对不同的载荷值，散粒体系统存在相应的暂时稳定状态，并且随着载荷大小的递增，系统达到稳定状态所需的时间越来越短，系统的变形也越来越小.

图8为不同时刻活塞和散粒体系统的位置.在数值计算中，可以跟踪每个颗粒在每个模拟时刻的位置和运动情况，图9为散粒体系统中编号为1的中层颗粒运动破碎过程.

图8 不同时刻活塞和散粒体系统位置图

从对每一个颗粒的跟踪中，可看出位于散粒体系统上层的颗粒首先被冲击破碎，且破碎情况最为严重，接近底部的中间颗粒基本没有破碎.最先破碎的颗粒为位于散粒体系统上层编号为161的颗粒，颗粒破碎时间为1.2 ms，这和活塞从1 ms开始运动相符合，也说明了数值计算的正确性.

4 结语

本文考虑了脆性颗粒材料的破碎，基于离散单元法将模拟单个脆性材料颗粒破坏过程的弹簧-球单元破碎模型应用到散粒体系统动力学分析中.对梯形载荷作用下的圆筒内伴随破碎的散粒体系统动力学问题进行了详细研究，得到了散粒体系统的变形行为和外部载荷之间的关系，获得了颗粒的破碎情况.本文的研究结果为发射装药发射安全性提供理论基础.

References)

[1] 吴爱祥，孙业志，刘湘平.散体动力学理论及其应用[M].北京:冶金工业出版社，2002:1-40.

[2] Cundall P A.A computer model for simulating progressive large scale movement in block rock system[C]//Symposium ISRM.Nancy，France，1971，2:129-136.

[3] 芮筱亭，王燕，王国平.弹药发射安全性试验方法进展[J].兵工自动化，2012，31(12):81-92.Rui Xiaoting，Wang Yan，Wang Guoping.Advances in test method of launch safety of ammunition[J].Ordnance Industry Automation，2012，31(12):81-92.(in Chinese)

[4] 洪俊，芮筱亭.梯形载荷下圆筒内粒子系统运动的数值仿真[J].系统仿真学报，2007，19(5):1007-1010.Hong Jun，Rui Xiaoting.Numerical simulation for granular system in barrel under ladder load[J].Journal of System Simulation，2007，19(5):1007-1010.(in Chinese)

[5] 姜世平，于海龙，芮筱亭，等.散体系统冲击破碎的动力学分析[J].爆炸与冲击，2014，34(2):247-251.Jiang Shiping，Yu Hailong，Rui Xiaoting，et al.Dynamic analysis on impact fragmentation of granular systems[J].Explosion and Shock Waves，2014，34(2):247-251.(in Chinese)

[6] Jiang S P，Rui X T，Hong J，et al.Numerical simulation of impact breakage of gun propellant charge[J].Granular Matter，2011，13(5):611-622.

[7] Shan L，Cheng M，Liu K X，et al.New discrete element models for three-dimensional impact problems[J].Chinese Physics Letters，2009，26(12):5-8.

[8] 洪俊，芮筱亭，费庆国.发射药床挤压破碎动力学仿真[J].系统仿真学报，2010，22(4):1018-1021.Hong Jun，Rui Xiaoting，Fei Qingguo.Dynamic simulation for propellant bed with press and fracture[J].Journal of System Simulation，2010，22(4):1018-1021.(in Chinese)

[9] Zang M Y，Lei Z，Wang S F.Investigation of impact fracture behavior of automobile laminated glass by 3D discrete element method[J].Computational Mechanics，2007，41(1):73-83.

[10] Mishra B K，Murty C V R.On the determination of contact parameters for realistic DEM simulations of ball mills[J].Powder Technology，2001，115(3):290-297.

[11] Liu J，You D X.Numerical simulation on dense packing of granular materials by container oscillation[J].Advances in MechanicalEngineering， 2013， 1:284693.