应用非概率凸集模型的框架结构抗震性能分析

王东超，徐龙军，张进国，谢礼立

（哈尔滨工业大学（威海）土木工程系，264209山东威海）

应用非概率凸集模型的框架结构抗震性能分析

王东超，徐龙军，张进国，谢礼立

（哈尔滨工业大学（威海）土木工程系，264209山东威海）

为解决结构抗震性能分析结果会因地震动记录选择上的差异产生较大变异性问题，采用非概率凸集模型来考虑地震作用的不确定性，以结构最大层间位移角作为抗震性能指标，通过能力谱方法对一钢筋混凝土框架结构进行非概率性抗震性能评估，与基于概率随机模型的抗震性能分析结果进行比较.结果表明，采用非概率凸集模型进行结构抗震性能分析，在减少变异性的同时，还具有一定的合理性和适用性.

不确定性；非概率；凸集模型；抗震性能；框架结构

由于地震发生的时间、空间以及地震动记录的频谱特性等均具有强烈的不确定性，因此结构在地震作用下的动力响应是一个不确定性问题.传统结构抗震性能分析是基于概率随机模型考虑结构不确定性响应；但是，这种分析方法会由于所选地震动记录数量和质量的不同，导致结果产生很大变异性.

上世纪90年代以来，国内外学者开始研究基于非概率凸集模型处理不确定性问题［1－3］.凸集模型所需实验数据较少，鲁棒性好，极大避免了概率随机模型的局限性［1］.其中文献［2］采用凸集模型描述不确定性参数，并将其应用于一个单自由度无阻尼的振动系统中，得到了该系统的非概率可靠度指标.此后，国内外学者基于凸集模型展开了多方面研究，并将其推广至地震工程领域［4－7］.文献［4］采用形状不确定但是能量有界的凸集模型考虑地震的不确定性作用；文献［6］基于规范提出了两个考虑工程参量的地震作用凸集模型.在实际工程抗震性能分析中，鉴于结构的不确定性参量有随机变量和非随机变量并存的情况，文献［8］提出通过逐次建立二级功能方程来求解混合模型下的非概率可靠度问题，这极大促进了非概率凸集理论在实际工程中的应用和发展.

在抗震性能分析方面，基于概率随机模型的抗震性能分析运算量大，计算复杂，分析结果容易受不同地震动记录选取问题的影响.鉴于此，本文采用非概率凸集模型来考虑地震作用的不确定性，以结构的最大层间位移角作为抗震性能指标，进而通过能力谱方法对一钢筋混凝土框架结构进行非概率性抗震性能评估，然后与基于概率随机模型的抗震性能评估结果进行分析比较.

1 结构体系抗震性能水准

结构抗震性能水准是指结构在某一特定设防地震作用下所预期达到的最大破坏程度［9］.随着基于性态的抗震设计思想的不断深化，对结构性能水平的划分也在不断细化，国内外总体上差别不大，但具体的量化指标仍有所不同.本文采用最大层间位移角表征结构的抗震性能，参考中国现行建筑抗震设计规范和文献［10］中结构的性能水平与层间位移角的关系，钢筋混凝土框架结构不同性能水平所对应的最大层间位移角θmax限值见表1.

本文主要考虑罕遇地震作用对结构的影响，只分析生命安全和接近倒塌两种性能水平下的抗震性能.不同性能水平下，结构能力参数对应的均值采用表1数值，并采用0.03的变异系数来考虑其不确定性.若将结构能力参数视作凸集模型，则采用加减一倍标准差确定其区间范围的上下界.

表1 钢筋混凝土框架结构各种性能水平下最大层间位移角θmax限值 rad

2 结构体系地震响应的不确定性分析

2.1 基于凸集模型的结构地震响应

采用文献［6］提出的双参数界限凸集模型描述地震作用的不确定性，这种方法有效考虑了水平地震影响系数最大值α 和特征周期T的影响：

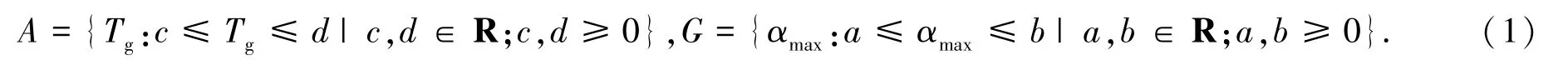
当αmax和Tg在包络界限G和A中取值时，水平 地震影响系数α的取值区间E为

在地震作用下，框架结构的变形以基本振型为主.研究表明［11］：对于高度不大的框架结构，受高阶振型影响较小，进行静力弹塑性分析可得到比较满意的结构弹塑性响应.通过能力谱方法将静力弹塑性分析得到的顶点位移—基底剪力能力曲线转化为A－D格式的能力谱曲线.通常采用FEMA［12］建议的方法对能力谱曲线进行等效双线性化处理.对于服从双线型本构关系的单自由度非弹性体系的抗力曲线，结构在地震动作用下的位移反应为

式中：Ry为屈服强度系数；Tn为等效单自由度体系的弹性周期；A是由弹性反应谱求得的结构最大加速度响应，可由式（2）中水平地震影响系数α的取值范围E得到；μ为延性系数.

2.2 基于随机变量的结构地震响应

传统抗震性能分析都是基于概率随机模型来考虑结构在地震作用下的不确定性响应，目前应用较多的结构易损性分析方法［13］也是基于这一理论出发的.在易损性分析中，通常假定结构的地震响应参数服从对数正态分布.结构工程的需求参数（D）和地震动参数（M）之间满足关系：

本文主要研究在地震作用下，结构最大层间位移角均值θ～max与地震动谱加速度Sa（T1，5%）的关系，代入上式两边同时取对数有

3 结构体系抗震性能分析

在不同性能水平下，结构的抗震性能可表示为结构的地震响应超过性能水准限值的概率.在概率性抗震性能分析中结构能力参数R和结构地震响应S均被视作随机变量，则结构的失效概率可表示为

假设R和S均服从对数正态分布，把式（4）、

（5）代入式（6），可得结构地震响应超过某一性能指标的超越概率为

式中：R的均值由不同性能水准下的层间位移角的限值确定；βR、βS根据 HAZUS99［14］取值，当以Sa（T1，5%）作为自变量时，βR2＋βS2取为0.4；Φ（·）表示标准正态分布.

在非概率抗震性能分析［1，5，7，15］中，R和S均被视作非随机变量，并采用凸集模型进行分析.根据变量间相关性的不同，凸集模型可以分为区间模型和椭球模型两种.关于非概率可靠度的求法，国内外学者分别提出了多种分析方法［16］，但是目前仍不存在一种普适性强的非概率可靠度分析方法.本文基于线性功能函数下采用最短距离法来分析结构的抗震性能.

线性功能函数方程为

式中ai、bj为常数，ri、sj为不确定变量.

若ri与sj视作区间模型，则ri、sj满足下式：

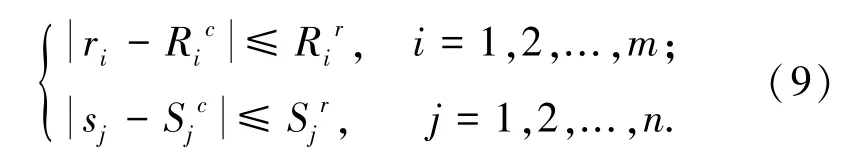
式中Ric、Sjc为不确定性变量的均值，Rir、Sjr为不确定性变量的离差.

区间模型的非概率可靠性指标可表示为

若ri与sj视作椭球模型，则ri、sj满足下式：

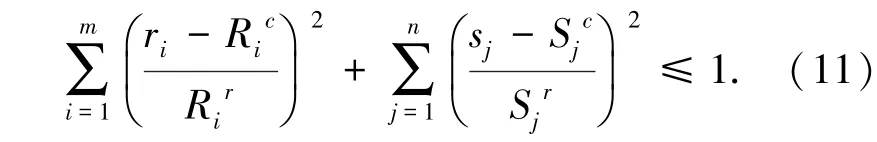
椭球模型的非概率可靠性指标可表示为

对于功能方程中既有随机变量又有非随机变量的情况，假设式（8）中ri为独立正态随机变量，sj为区间变量.当两变量可以分离时，考虑ri的随机性，可以构造二级功能方程来求解得到概率－非概率混合模型可靠性指标［5，8］，当R＝r时其公式为

从而建立二级功能方程为

由式（14）得到混合模型的可靠性指标为

4 算例分析

采用上述方法评估一六层三跨钢筋混凝土框架的抗震性能.结构按照现行抗震规范进行设计，抗震等级为二级，设防烈度为八度（0.20 g），设计地震动分组为第一组.由于结构在空间上的对称性，并且本文假定地震动沿结构主轴方向输入，因此本文结构抗震性能分析是基于中间一榀平面框架进行的，计算简图见图1.在该框架结构的设计中，底层高4.2 m，其余各层高3.6 m，结构总高22.2 m.梁柱纵向钢筋均采用HRB400，梁柱混凝土等级均取C30，板厚为100 mm，梁柱截面尺寸及配筋见表2.

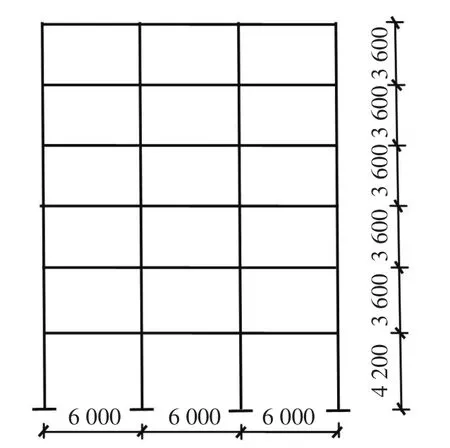
图1 框架结构计算简图（mm）

表2 框架结构构件截面尺寸及配筋

采用有限元软件OpenSees进行建模，混凝土采用单轴Kent-Scott-Park模型，考虑了约束箍筋对混凝土强度和极限压应变的提高作用，同时考虑了混凝土的拉伸硬化.钢筋采用Steel01Material（即双折线本构模型）.结构的竖向荷载根据抗震设计规范（GB50011—2010）中5.1.3条规定对恒载、活载进行一定组合后作为结构的重力荷载代表值.结构阻尼采用Rayleigh阻尼模型，对于钢筋混凝土结构，按照规范规定取其阻尼比为0.05.经过模态分析可得结构的基本周期T1＝0.94 s.

若结构的地震响应视作非随机变量，则基于非概率凸集模型按照上述方法分析结构响应的不确定范围.采用文献［17］指出的8度罕遇地震下水平地震影响系数αmax和Ⅱ类场地特征周期Tg的取值范围.通过对结构采用一阶振型的侧力加载模式进行静力弹塑性分析，能力谱曲线见图2.结构在罕遇地震作用下结构顶点位移响应区间为（178mm，520mm），对应的结构最大层间位移角的响应区间为（0.012 1 rad，0.041 6 rad），相应于两种性能水准的限值要求，结构的抗震性能分析结果见表3.

若结构的地震响应视作随机变量，则需要对结构进行一系列时程分析.为了使所选择的地震动记录尽可能地反映场地的工程特点，规范要求地震动反应谱与设计反应谱在统计意义上具有一致性.按照文献［18］中提出的双频率段选波的方式选择了12条强震记录，地震动信息见表3.经适当调幅后，其加速度反应谱、平均反应谱与设计反应谱比较见图3.分析可知，所选地震动记录在［0.1，Tg］平台段和结构基本周期T1附近加速度反应谱均值与设计反应谱均值能较好拟合，相差均不超过10%，满足统计意义上一致性的要求.

图2 框架结构能力谱曲线

表3 地震信息表

图3 本文所选记录加速度谱与设计谱对比

按照增量动力分析方法［19］，对所选的12条地震动的谱加速度Sa（T1，5%）以0.1g为增量不断调幅后，对结构进行非线性动力时程分析.对所得数据进行统计回归分析，数据处理见图4.可以看出结构在相同谱加速度的不同地震动记录作用下，得到的结构响应结果具有较大的离散性和变异性.依据建筑抗震设计规范计算，结构的响应加速度为0.37g.按照上述方法，结构易损性分析结果见图5，并与非概率抗震性能分析结果对比见表4.

图4 以Ln（Sa（T1，5%））为自变量的Ln（θmax）回归分析

基于两种性能水准的限值要求下，相比于概率随机模型，非概率模型计算的超越概率偏大，但是相差在5%以内.当Rc－Sc＜0时，相比于区间模型，椭球模型虽然在一定程度上考虑了变量之间的相关性，但计算结果要比区间模型偏大，当Rc－Sc＞0时则情况相反.在混合模型计算中，结构的地震响应和能力参数分别采用随机变量和区间变量考虑其不确定性，相当于“响应宽”、“限值窄”，因此计算结果较其他模型偏大一些.

图5 框架结构易损性曲线

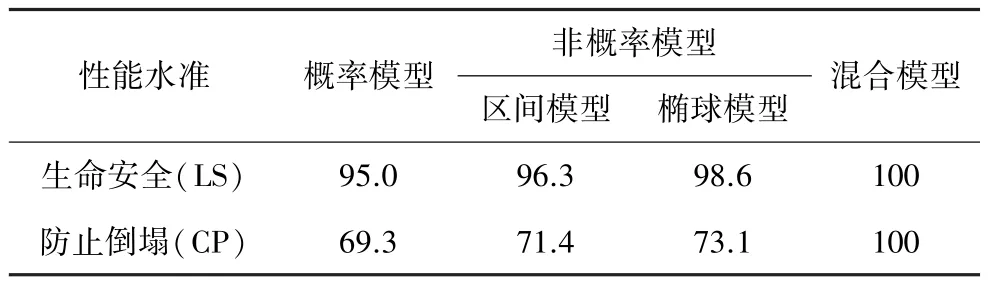
表4 框架结构概率与非概率抗震性能分析结果对比 %

5 结 论

1）对于地震这一不确定性强烈的工程问题，采用考虑水平地震影响系数αmax和特征周期Tg的双参数界限凸集模型分析其不确定性作用，更能符合工程实际，避免了结构进行概率性抗震性能分析时结果会因不同的地震动选择产生较大变异性的问题.

2）在相关参数取值合理的情况下，相比于概率随机模型，基于非概率凸集模型的抗震性能分析方法，避免了大量的复杂运算，计算更加简便，通过对一钢筋混凝土框架结构算例分析，验证了方法的合理性与可行性.

3）由于非概率抗震性能分析是基于能力谱方法出发的，因此其适用于高度不大，变形以基本振型为主，且受高阶振型影响较小的结构形式，比如高度低于40 m的框架结构.

［1］JIANG Chao，BI Rengui，LU Guoying，et al.Structural reliability analysis using non-probabilistic convex model［J］.Computer Methods in Applied Mechanics and Engineering，2013，254：83－98.

［2］BEN-HAIM Y，ELISHAKOFF I. Convex models of uncertainty in applied mechanics［M］.Amsterdam：Elsevier Science Publisher，1990.

［3］JIANG Chao，LI Wenxue，HAN Xu，et al.Structural reliability analysis based on random distributions with interval parameters［J］.Computers＆Structures，2011，89（23）：2292－2302.

［4］TZAN S R，PANTELIDES C P.Convex models for impulsive response ofstructures［J］.Journal of Engineering Mechanics，1996，122（6）：521－528.

［5］JIANG Chao，HAN Xu，LI Wenxue，et al.A hybrid reliability approach based on probability and interval for uncertain structures［J］.ASME，Journal of Mechanical Design，2012，134（3）：1－11.

［6］张之颖，张景绘.反应谱参量双界限凸集模型及其地震作用效应［J］.西安交通大学学报，1999，33（2）：46－50.

［7］JIANG Chao，NIBingyu，HAN Xu，et al.Non-probabilistic convex model process：A new method of time-variant uncertainty analysis and its application to structural dynamic reliability problems［J］.Computer Methods in Applied Mechanics and Engineering，2014，268：656－676.

［8］郭书祥，吕震宙.结构可靠性分析的概率和非概率混合模型［J］.机械强度，2002，24（4）：524－526.

［9］JANG Huanjun，CHEN Linzhi， CHEN Qian.Seismic damage assessment and performance levels of reinforced concretemembers［J］.Procedia Engineering，2011，14：939－945.

［10］李刚，程耿东.基于性能的结构抗震设计——理论、方法与应用［M］.北京：科学出版社，2004.

［11］KRAWINKLER H，SENEVIRATION G D P K.Pros and cons of a push-over analysis of seismic performance evaluation［J］.Engineering Structure，1998，20（5）：452－464.

［12］FEMA273.NEHRP guidelines for the seismic rehabilitation of building［S］.Washington D C：Federal Emergency Management Agency，1997.

［13］BAI JW.Seismic fragility analysis and loss estimation for concrete structures［D］.College Station：Texas A＆M University，2011.

［14］FEMA366.HAZUS 99 estimated annualized earthquake looses for the United States［S］.Washington D C：Federal Emergency Management Agency，2001.

［15］BAIYingchun，HAN Xu，JIANG Chao，et al.A responsesurface-based structural reliability analysismethod by using non-probability convex model［J］.Applied Mathematical Modeling，2014，38：3834－3847.

［16］王睿星，王晓军，王磊，等.几种结构非概率可靠性模型的比较研究［J］.应用数学与力学，2013，34（8）：871－880.

［17］贾立哲，段忠东，陆钦年.基于凸集模型的界限Pushover分析［J］.地震工程与工程振动，2006，26（5）：81－87.

［18］杨溥，李英民，赖明.结构时程分析法输入地震波的选择控制指标［J］.土木工程学报，2000，33（6）：33－37.

［19］VAMVATSIKOSD，CORNELL A C.Incremental dynamicanalysis［J］.Earthquake Engineering＆Structure Dynamics.2002，31（3）：491－514.

（编辑赵丽莹）

Analysis on seismic performance of frame structure using non-probabilistic convexmodel

WANG Dongchao，XU Longjun，ZHANG Jinguo，XIE Lili

（Department of Civil Engineering，Harbin Institute of Technology atWeihai，264209Weihai，Shandong，China）

Convexmodelwas used to consider the uncertainty of earthquake in this paper to solve the problem that the selection of different ground motion records will result in great variability in structural seismic performance analysis.Taking the inter-story displacement angle as seismic performance index，non-probabilistic seismic performance of a reinforced concrete frame was assessed under the motivation of rare earthquake by the capability spectrum analysis method.Then the results were compared with probabilistic seismic performance based on the probabilistic random model.By comparison and analysis，it shows that the evaluation of structural seismic performance based on convexmodel not only reduces the variability，but also is reasonable and applicable to some extent.

uncertainty；non-probabilistic；convexmodel；seismic performance；frame structure

TU312；TU375

A

0367－6234（2015）12－0045－05

10.11918／j.issn.0367-6234.2015.12.008

2014－06－06.

国家自然科学基金重大研究计划项目（91215301）；山东省蓝区工程建设与安全协同创新中心资助；山东省科技发展计划（2014GSF122001）.

王东超（1992—），男，硕士研究生；徐龙军（1976—），男，教授，博士生导师；谢礼立（1939—），男，博士生导师，中国工程院院士.

徐龙军，xulongjun80＠163.com.