“磁滞刹车”现象中暂态过程的研究

赵芸赫，马宇翰

(北京师范大学 物理学系，北京 100875)

“磁滞刹车”现象中暂态过程的研究

赵芸赫，马宇翰

(北京师范大学 物理学系，北京 100875)

摘要：基于磁滞刹车中的暂态问题设计实验，测量了磁铁磁场的径向分布，在此基础上对磁偶极子模型给出的磁场分布做了修正；数值计算了阻力表达式中积分项，并用双曲正切函数拟合给出了阻力表达式中积分部分的经验公式，简化了动力学方程的求解. 理论计算并实时测量了磁铁运动的速度，研究了从磁铁开始受到磁滞力到达到匀速运动之前的减速暂态过程以及离开管口后的加速暂态过程.

关键词：磁滞刹车；暂态过程；磁场分布

1概述

当强磁铁沿非铁磁性材料的管下降时，通常会观察到有趣的物理现象：磁铁将会受到磁滞力，即“磁滞刹车”现象. 对于该现象，目前有大量的研究报道. 其中Gren Ireson[1-5]等研究了磁铁在铜管中运动现象，C. S. MacLatchy[6]等研究了不同质量的磁铁及多个磁铁在铜管中的运动现象，G. Donoso[7]等还探究了磁铁在不同材质、不同管厚的金属管中的运动现象. 除此之外，K. D. Hahn, R. Stanway[8-9]等研究了铜管内的感应电流分布，Guillermo Donoso，Celso L.Ladera[10]等人对于图1[5]中所示的磁铁在铜管中的运动，采用在管上取微元导线的方法，并将磁铁的径向磁场分布用磁偶极子的径向磁场分布代替，给出了磁场的分布为

(1)

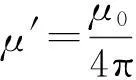
图1　磁铁在铜管中运动示意图

(2)

其中σ为电导率，R1和R2分别为铜管的内外半径，L为管长，式中还做了z-h=R1u的代换. (2)式中的积分项是随着磁铁所处位置的变化而变化的，但是由于该值在磁铁即将进入管中时迅速从零增大为一定值，所以通常人们将管作无限长处理，这样积分值为一定值，但是这种近似在管口处是失效的，无法确切描述磁铁的暂态运动. 目前大部分的研究工作主要对磁铁达到匀速稳态时的速度进行了探究，对于磁滞刹车减速部分的暂态运动的研究很少. 而实际上磁滞刹车过程中磁铁的加速度从g到0不断改变，刹车过程主要与暂态过程相关联.

本文设计实验测量了磁铁磁场的径向分布，在此基础上对磁偶极子模型给出的磁场分布做了修正，并对用简单函数双曲正切拟合给出了阻力表达式中积分部分的经验公式，简化了动力学方程的求解. 在此基础上理论计算了磁铁运动整个过程的速度，并设计实验，实时测量了磁铁运动的速度，研究了从磁铁开始受到磁滞力到达到匀速运动之前的暂态过程.

2磁铁运动的理论模型

2.1　阻力系数形式的确定

将式(2)中的积分项近似为一定值，无法解释管口附近复杂的暂态现象. 为了研究暂态过程，令(2)式中的积分为

(3)

定义阻力系数为k，则

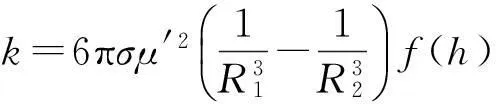
(4)

k与f(h)成正比，于是，磁铁运动的动力学方程可以写为

ma=mg-k(h)v.

(5)

采用数值计算得到的积分f(h)的值随磁铁所处位置的变化关系如图2所示. 可以看出，在管口上方，积分值f(h)从零开始迅速增大，进入管内迅速稳定为一定值，出管外一小段距离后迅速降为零． 这表明磁铁未进入管时，磁滞力已经开始起作用，当磁铁离开管的一小段距离内，磁滞力仍在起作用． 这也与楞次定律相符合．

图2　f值随距离上管口的位置h的变化曲线(h=0对应管口，管长L=1.0 m)

磁铁运动初期，加速度不断减小，通过观察分析f(h)曲线的趋势，采用具有2个未知参量的经验公式f(h)=γ(tanhβh+1)进行拟合该曲线，得到的拟合曲线与数值计算的结果如图3所示，经验公式拟合的结果与数值计算结果比较符合，可以确定γ=0.061 4；β=102.3 m-1. 可以得到磁滞力系数k的解析表达式为

(6)

这样可以简化磁铁运动的动力学方程.

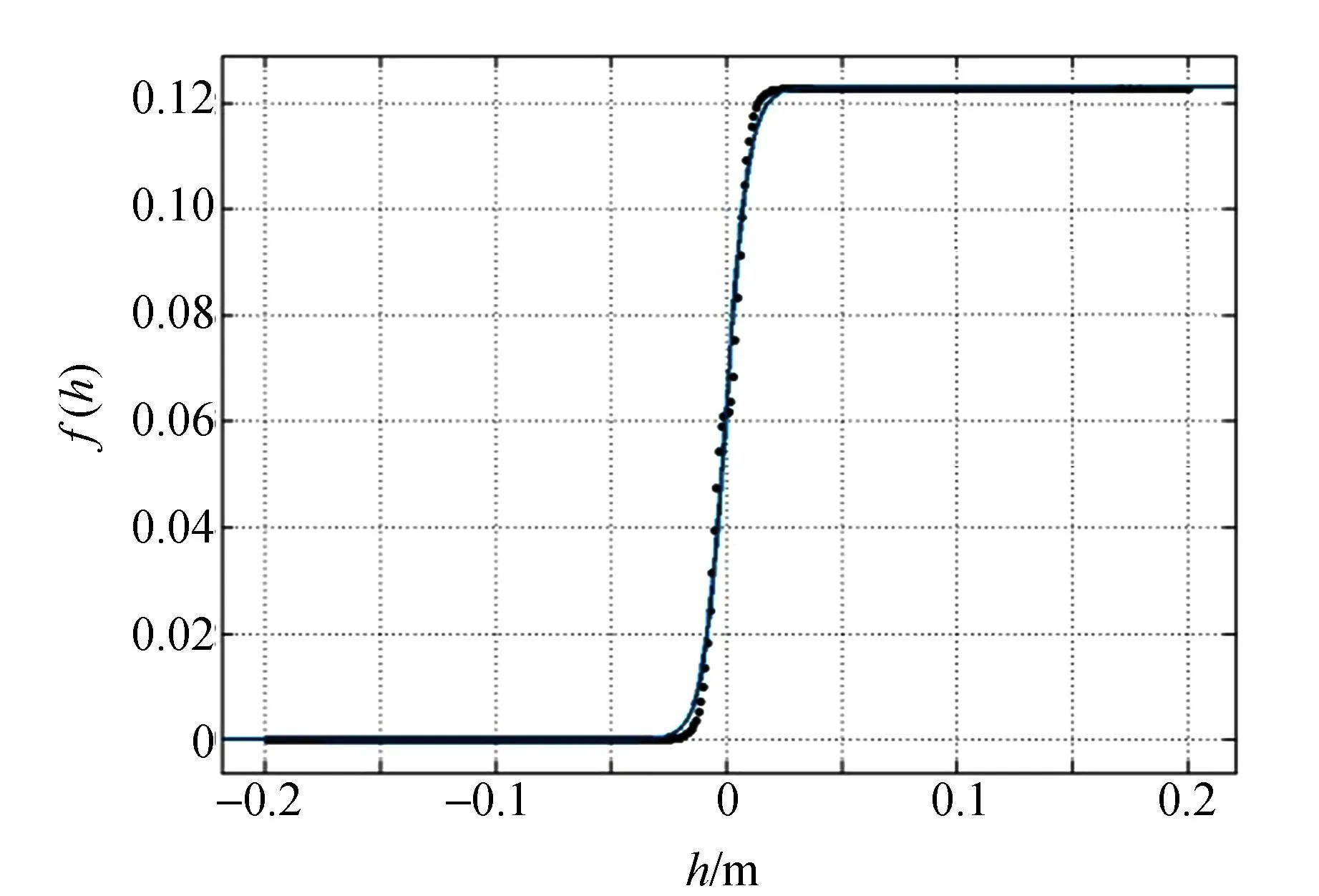
图3　经验公式拟合与数值计算的f随h变化的曲线

2.2　磁偶极子径向磁场表达式的修正及磁铁运动的理论模拟

要理论计算磁铁的运动速度，需要知道磁场的具体分布. 为了确定磁偶极子模型表示的磁场的径向分布是否与磁铁的真实磁场分布一致，采用图4所示的设备测量了规格为15 mm×19 mm的强磁铁的磁场分布，如图5所示. 同时采用磁偶极子径向磁场表达式拟合的磁场分布也示于图5中.

图4　测量磁铁径向磁场分布的实验装置示意图

图5　实验测量及采用磁偶极子模型计算的磁铁的径向磁场分布结果

可以看出，实际磁场分布与计算曲线有一定差异，为了消除这一差异，引入修正因子α，将径向磁场表示为

(7)

采用修正后的磁场分布关系拟合的磁场分布与实验测量的对比结果如图6所示，可以看出两者几乎完全重合，并可以得到该规格磁铁的α=0.918 5. 后续实验所用到的其他规格的磁铁也用同样方法拟合给出修正因子．

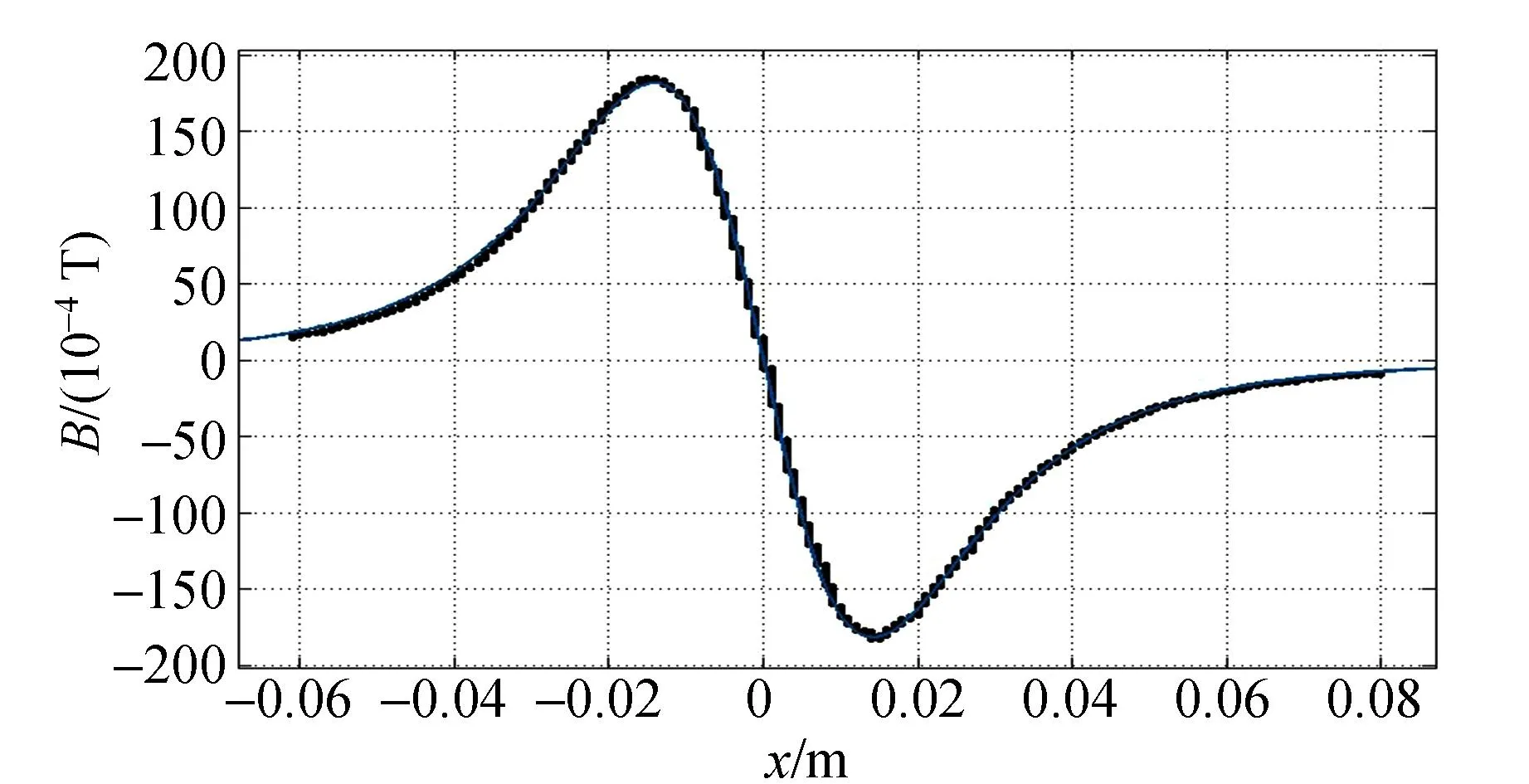
图6　实验测量及采用修正后的磁偶极子模型计算的磁铁的径向磁场分布结果

至此，修正后的阻力系数k变为

(8)

则基于动力学方程ma=mg-k(h)v，以磁铁距上管口17.2 cm处释放的情形为例，对于磁铁自管外释放开始数值计算磁铁整个过程中的速度随着距释放位置的距离的变化关系，如图7所示. 磁铁在释放后，经历了加速—减速—匀速—加速的过程. 对于磁滞刹车来说，减速过程才是刹车的精髓.

图7　数值计算的磁铁的运动速度随距释放位置距离变化的关系

3磁铁运动现象的研究

3.1　磁铁运动过程中重力和磁滞力之外因素影响的修正

采用图8所示的实验装置测量了磁铁释放之后的运动过程，为了避免铁磁性材料对实验现象的影响，采用塑料制品对铜管固定；为了排除每次用手释放的不确定因素，采用电磁铁释放开关释放磁铁；为了保证磁铁在管外的运动也沿铜管轴线方向以及调节磁铁的初速度，在铜管内又嵌套了玻璃管，其露出铜管外的高度可以自由调节；为了测量强磁铁在管中的运动，在其下方连接了塑料杆并做标记，且由于暂态过程的短暂，采用高速相机抓拍记录.

图8　实验装置及其示意图

在空气环境中磁铁在玻璃管内运动，距释放位置的距离随时间的变化关系如图9所示，采用二次关系拟合曲线，得到的加速度的数值a=8.754 N/kg<9.8 N/kg．显然，磁铁运动过程中还受到除重力和磁滞力之外力的作用. 因此将其他阻力，如空气阻力、磁铁与玻璃管的摩擦等的作用效果加在重力加速度上，并替换其为等效重力加速度(拟合的g′值)，则动力学方程变为ma=mg′-k(h)v. 对于每次实验都重新拟合这一数值，以符合实际情况．

图9　空气环境中磁铁在玻璃管内的运动及二次关系拟合曲线

3.2　不同质量的磁铁的磁滞刹车现象

图10为实验测量和理论计算的不同等效重力下，磁铁的运动速度随距释放位置的距离的变化曲线，理论和实验基本吻合，说明求解动力学方程的结果是可行的. 此外，从曲线可以看出，其他实验条件相同的情况下，磁铁质量越小，曲线加速部分斜率绝对值越大，即磁铁加速度的变化越明显，则暂态过程的刹车现象越明显，所达到的稳态速度越小. 此外，由图中磁铁加速度变化的趋势可以预测当其质量增大到某一值时，磁铁进管后将无减速现象.

图10　不同质量磁铁的“磁滞刹车”

图11为磁铁达到匀速运动状态时的稳态速度随等效重力的变化曲线，可以看到曲线呈良好的线性关系，这表明，在其他实验条件相同的情况下，仅改变磁铁质量，其在铜管中达到匀速时的k值为常量，这与文献报道的结果一致[2]. 这也表明通过给出的经验公式求解动力学方程描述磁滞刹车现象是可行的.

图11　稳态速度随等效重力的变化图像

3.3　在不同规格的铜管运动的磁铁的磁滞刹车现象

为了探究在不同管中磁铁运动的暂态过程，进一步用不同规格的铜管与磁铁进行实验. 1号铜管和磁铁：铜管外径为28.60 mm，铜管内径为24.72 mm，磁铁规格20 mm×19 mm，电导为4.251 4×107S,磁偶极矩μ′为13.5×10-8A·m2. 2号铜管和磁铁：铜管外径为24.80 mm，铜管内径为21.62 mm，磁铁规格15 mm×19 mm，电导为5.714 3×107S,磁偶极矩μ′为8.8×10-8A·m2. 图12和13分别为使用2组实验器材，在距离铜管管口的不同高度释放磁铁后，实验测量及理论计算的运动速度随距释放位置距离变化的曲线. 从图上可以看出，实验与理论符合较好，验证了理论的正确性．

图12　不同进管初速度的磁铁速度随着距释放位置的距离变化曲线(1号铜管实验与理论)

图13　不同进管初速度的磁铁速度随着距释放位置的距离变化曲线(2号铜管实验与理论)

4结束语

从理论和实验方面研究了磁滞刹车现象中的暂态过程. 设计实验测量了磁铁的磁场分布，在偶极子近似模型的磁场分布中，引入修正因子使其更符合实际磁铁的磁场分布；用tanhx函数拟合了数值计算的磁滞力表达式中的积分项f(h)，进而给出磁滞刹车现象中阻力系数的经验公式, 简化了磁刹车动力学方程的求解；用高速相机等其他实验装置和方法准确地记录并分析了这一过程，与理论符合很好.

参考文献：

[1]IresonG,TwidleJ.Magneticbrakingrevisited:activitiesfortheundergraduatelaboratory[J].Eur.

J.Phys., 2008,29(4):745-751.

[2]PartoviMH,MorrisEJ.Electrodynamicsofamagnetmovingthroughaconductingpipe[J].Can.J.Phys., 2006,84:253-271.

[3]LevinY,daSilveiraSL,RizzatoFB.Electromagneticbraking:asimplequantitativemodel[J].Am.J.Phys., 2006,74(9):815-817 .

[4]WiederickHD,GauthierN,CampbellDA,etal.Magneticbraking:Simpletheoryandexperiment[J].Am.J.Phys., 1987,55(6):500-503.

[5]Bostock-SmithJM.ThejumpingringandLenz’slaw—ananalysis[J].Phys.Educ., 2008,43(3):265-9.

[6]MacLatchyCS,BackmanP,BoganL.Aquantitativemagneticbrakingexperiment[J].Am.J.Phys., 1993,61(12):1096-1106.

[7]DonosoG,LaderaCL,MartínP.Magnetfallinsideaconductivepipe:Motionandtheroleofthepipewallthickness[J].Eur.J.Phys., 2009,30(4):855-869.

[8]HahnKD,JohnsonEM,BrokkenA,etal.Eddycurrentdampingofamagnetmovingthroughapipe[J].Am.J.Phys., 1998,66(12):1066-1076.

[9]StanwayR.Smartfluids:Currentandfuturedevelopments[J].Mater.Sci.Technol., 2004,20(8):931-939.

[10] Donoso G, Ladera C L, Martin P. Damped fall of magnets inside a conducting pipe [J]. Am. J. Phys., 2011,79(2):193-200.

[责任编辑：任德香]

Research on the transient state of magnetic brakes

ZHAO Yun-he， MA Yu-han

(Department of Physics, Beijing Normal University, Beijing 100875, China)

Abstract:Based on the transient state of magnetic brakes, the radial magnetic fields of the magnets were measured, which was a basis of the correction of the magnetic dipole. Numerical integral of the retarding force was calculated, and an empirical formula was given using hyperbolic tangent function, thus the solution of the dynamic equation was simplified. The velocity of the magnet during the whole process was calculated theoretically and studied in real time, the deceleration and acceleration processes were investigated, respectively.

Key words:magnetic brake; transient state; magnetic field distribution

中图分类号：O441

文献标识码：A

文章编号：1005-4642(2015)04-0007-05

作者简介：赵芸赫(1993-)，女，吉林长春人，北京师范大学物理学系2012级本科生.

收稿日期：2014-12-09；修改日期：2015-01-29