天平振动的研究

冯　娟，汪冬亮，范　克，胡　煜

(中国地质大学(北京) 物理实验教学示范中心,北京 100083)

天平振动的研究

冯娟，汪冬亮，范克，胡煜

(中国地质大学(北京) 物理实验教学示范中心,北京 100083)

摘要：根据力矩平衡关系，讨论了天平的振动规律. 通过测量天平的感度和振动周期，考查了天平的转动惯量、重心位置等参量，分析了天平感度随称量量的变化规律，加深了对天平的认识.

关键词：天平；感度；周期；转动惯量

1方法原理

天平是测量物体质量的常用仪器. 在讨论天平时，通常假定3个刀口(两侧刀口和中间刀口)在同一水平面上[1-2]，如图1所示. 设天平臂长为l，横梁的重心C到中间刀口B0的距离为h，L为中间刀口B0到底部标尺的距离，横梁的质量为m0，g为重力加速度. 当天平两侧的负载分别为m和m+Δm时，指针向负载m侧偏转. 如果Δm不是太大，偏转角为φ时又达到新的平衡，有

mglcosφ+m0ghsinφ=(m+Δm)glcosφ,

整理后，可得

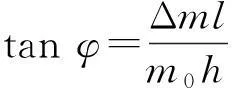
实际上,天平的3个刀口不可能在同一平面上，如图2所示[3]. 设中间刀口B0到两侧刀口B1和B2平面的距离为λ，∠B0B1B2=θ，两侧负载合力的作用点不在B0，这时又产生新的恢复力矩2mgλsinφ，即

Δmglcos (θ+φ)=m0ghsinφ+2mgλsinφ,

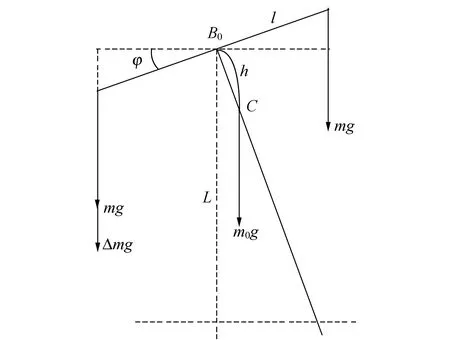
图1　理想天平平衡示意图

由于实际上θ≪φ，cos (θ+φ)≈cosφ，所以

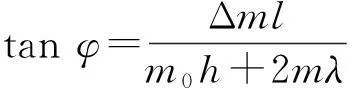
(1)

式中m是秤盘质量m1和砝码质量m2之和. 从(1)式可以看出，天平偏转角φ不仅和差额质量Δm有关，而且也和天平的负载有关.

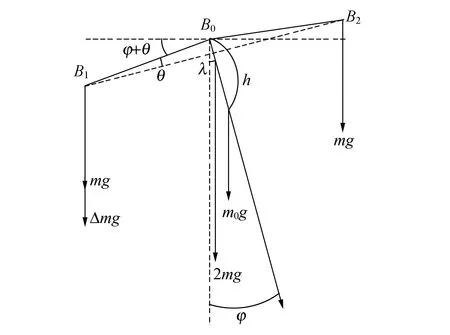
图2　实际天平平衡示意图

设指针偏转角度φ时，指针在底部标尺上移过的距离为s有

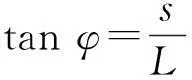
(2)

将(2)式代入(1)式，可得

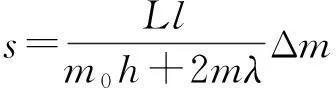
(3)

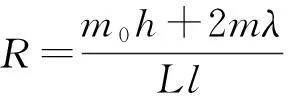
(4)

天平振动时近似为复摆(严格讲，托盘与横梁间有相对运动，不能看成刚体)，振动周期T应当等于

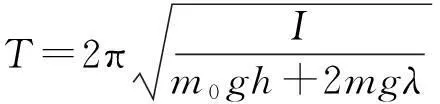
(5)

式中,I为天平对支点B0的转动惯量，I由2部分组成，即天平梁的转动惯量I0、秤盘和砝码的等效近似转动惯量. 现将秤盘和砝码均简化为横梁一端的质点，其转动惯量可写为2(m1+m2)l2+λ2，λ远小于l，取近似式则有

I=I0+2(m1+m2)l2.

又设I01=I0+2m1l2，它是梁和秤盘的转动惯量之和，因而

I=I01+2m2l2,

(6)

综合(4)~(6)式可得

(7)

(8)

制造天平时总希望R与m2无关，即尽量使λ(来源于制造误差)最小.RT2和R与砝码质量m2均呈线性关系：

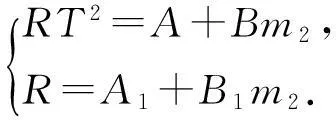
(9)

由(9)式可知，测量出不同砝码质量m2对应的感度R及振动周期T，则可解方程组(9)，求出参量A,B,A1,B1；再根据(7)式和(8)式以及测出的L,l,m0和m1，就可求出：

1) 空载感度R0，即A1;

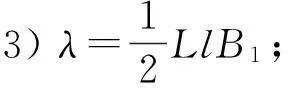
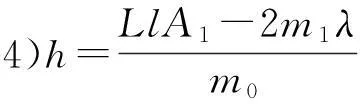
2实验方案

实验装置图如图3所示[2].

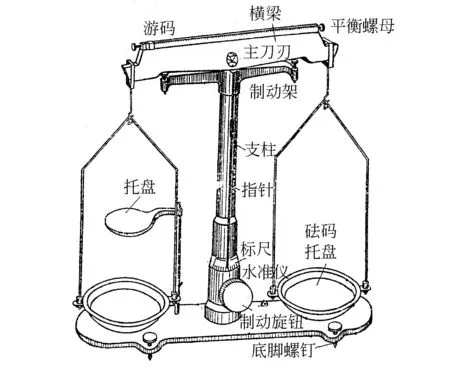
图3　测量天平振动实验装置图

2.1　测量常量

中间刀口到标尺距离L,力臂长度l,梁的质量m0,秤盘的质量m1,指针标尺的长度20a(a为1 div宽度).

2.2　测量振动周期T和感度R

测出当m2(两侧盘上加同样砝码)等于0时的振动周期T和感度R，然后在左盘加入Δm=10 mg的砝码，测出此时的振动周期T和感度R，记录数据. 改变m2分别为20,40,60,80,100 g，重复上述操作.

3数据分析

测出梁的质量m0=131.40 g；臂长l=11.83 cm；秤盘的质量m1=119.80 g；中间刀口到标尺的距离L=24.11 cm. 周期和感度的测量数据如表1 和表2所示.

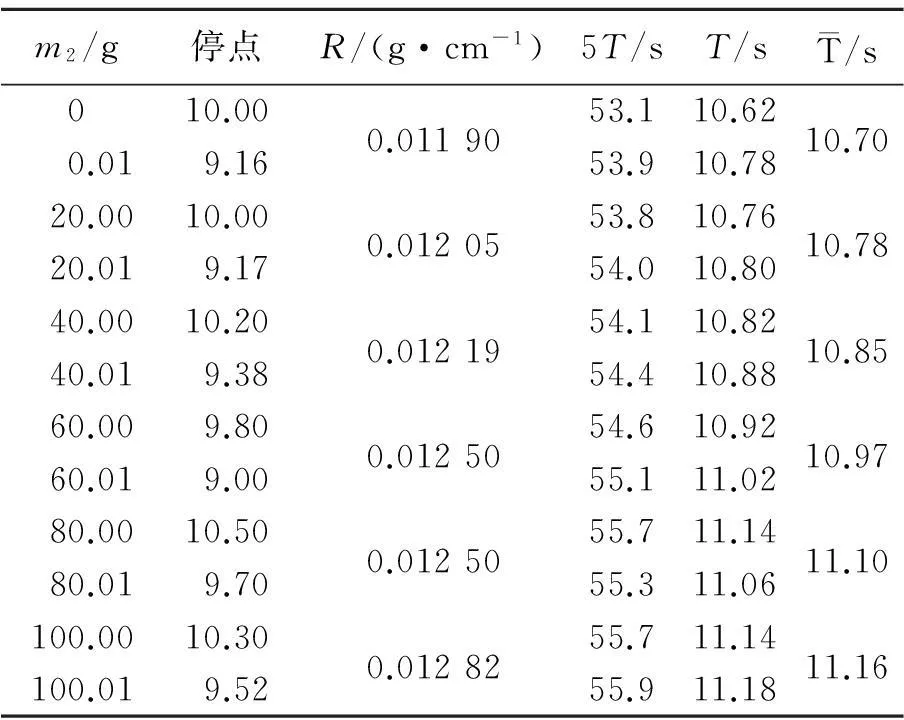
表1　周期和感度的测量

R，RT2与砝码质量m2的关系如图4~5所示. 由图可以看出，除部分点偏差较大以外，R,RT2与m2呈线性相关. 引起误差的原因主要是周期和停点测量不准确. 通过直线拟和可求出：

A=1.354 6 g·s2/cm，B=0.002 4 s2/cm,

A1=0.011 9 g/cm，B1=8.9×10-6cm-1.

最后求出：

R0= 0.011 9 g/cm,

I01=1.60×105g·cm2,

λ=0.001 3 cm,h= 0.023 5 cm.

由R-m2曲线图可知，随着m2增加，感度近似呈线性缓慢增加， 故灵敏度随着质量的增加而减小. 空载感度最大，R0= 0.011 9 g/cm. 天平的感度还与重心位置有关，本文所用天平的重心位置在中间刀口B0下方h=0.023 5 cm处. 调节重心螺丝(感量砣)，可以改变和校准感度. 一般负载越轻，横梁越轻，重心越高，灵敏度越高. 中间刀口B0到两侧刀口B1和B2平面有一微小的距离λ=0.001 3 cm，λ来源于制造误差，是仪器本身的固有缺陷.

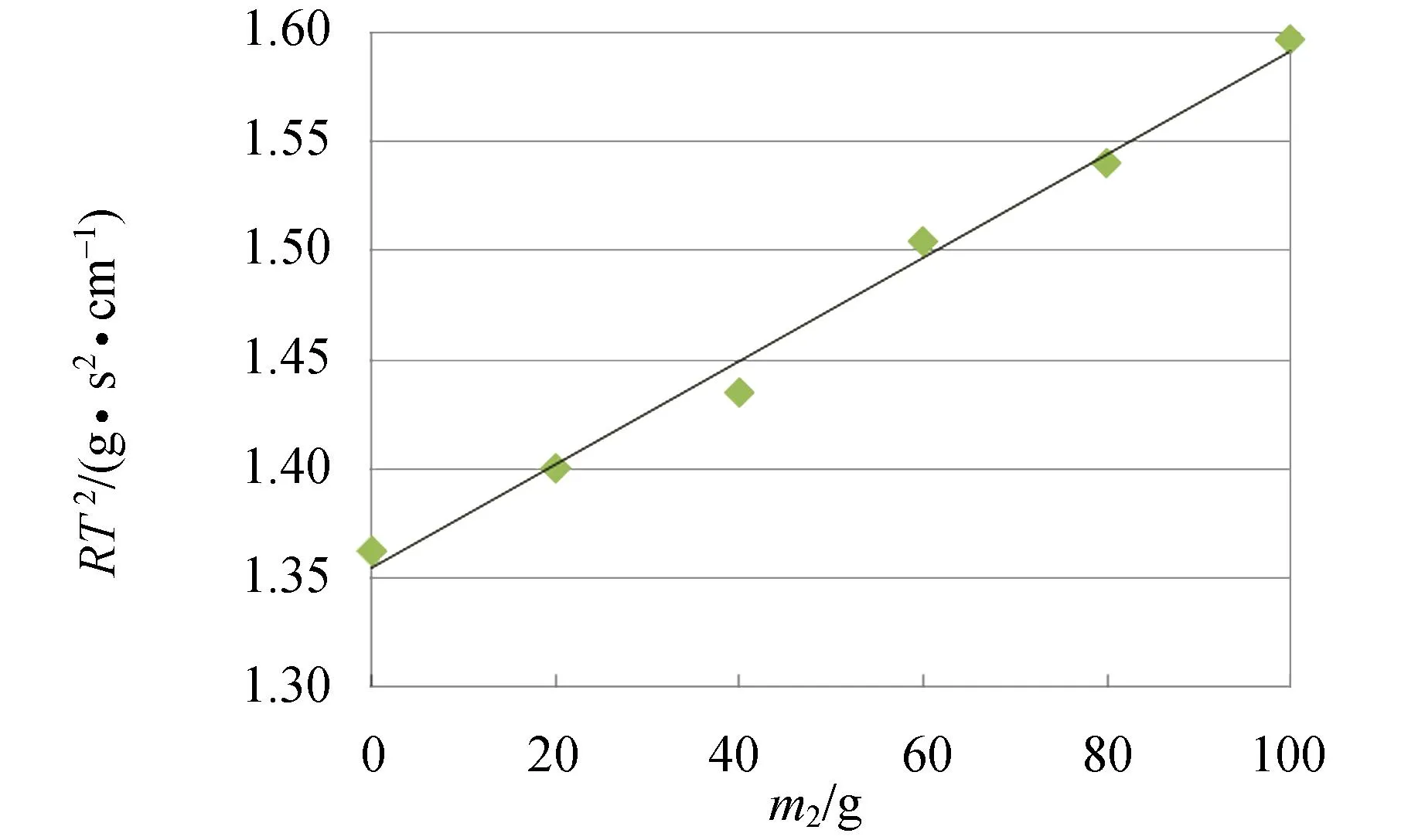
图5　RT2-m2图

4结束语

根据力矩平衡关系，分析了天平的机械振动规律. 通过测量天平的感度和振动周期，考查了天平的转动惯量、重心位置等参量，分析了天平感度随称量量的变化规律，加深了对天平的认识.

参考文献：

[1]周惟公. 大学物理实验[M]. 北京: 高等教育出版社,2009.

[2]华中工学院,天津大学,上海交通大学. 物理实验[M]. 北京:高等教育出版社,1981.

[3]杨述武. 普通物理实验[M]. 北京：高等教育出版社，2002.

[责任编辑：郭伟]

Research on vibration of balance

FENG Juan, WANG Dong-liang, FAN Ke, HU Yu

(Demonstration Center of Physics Experiment， China University of Geosciences， Beijing 100083， China)

Abstract:According to the torque balance equation, the vibration of balance was discussed. By measuring the sensitivity of the balance and the period of the vibration, the moment of inertia and the center of gravity were examined. The dependence of the sensitivity on weigh was analyzed and the understanding about balance was deepened.

Key words:balance; sensitivity; vibration period; moment of inertia

中图分类号：O312.2;TH715.11

文献标识码：A

文章编号：1005-4642(2015)04-0025-03

作者简介：冯娟(1976-)，女，山东德州人，中国地质大学(北京)物理实验教学示范中心讲师，博士研究生，主要从事实验物理教学和应用地球物理学领域的研究.

收稿日期：2014-06-20；修改日期：2014-09-14

“第8届全国高等学校物理实验教学研讨会”论文

资助项目：2012年中国地质大学教学研究与教学改革项目资助(No.JGYB-201233)