风电-抽水蓄能联合运营利润分配研究

卢 姬，常俊晓，熊洋建

（1.三峡大学 电气与新能源学院，湖北宜昌443002；2.国网湖北省荆州供电公司检修分公司，湖北荆州434000）

0 引 言

由于风能具有随机波动和反调峰等特性，使得大规模风电场的风电并网容量大大受限。2013年全国弃风损失达到16.2 TWh，给风电企业带来巨大的经济损失。因此，提高电力系统调峰能力是解决风电消纳问题的关键，抽水蓄能电站是目前最为成熟可靠的调峰电源，其机组具有运行速度快、反应灵活的特点，调峰系数可达200%，这是其他调峰电源无法做到的［1-2］。利用抽水蓄能电站响应灵活的特点，与风电场联合运营，和风电的随机波动性形成互补，有利于提高风电的并网量和保障电网的稳定运行［3］。

目前，国内外对风电场与抽水蓄能电站联合运营的研究主要有：联合优化运行模型［4，5］，联合系统能量转换效益研究［6］，联合系统容量规划方法研究［7］，但很少涉及利润分配。正确处理两者之间的利益分配问题，是风电场与抽水蓄能电站能够长期良好联合运营的前提。为此，本文研究了风电与抽水蓄能电站联合运营下的利润分配问题。

1 发电企业的成本

发电企业的成本主要来自四个方面：建设成本、运行维护成本、资金成本以及燃料成本。相对于常规能源发电，可再生能源发电最显著的特点是不需要考虑燃料成本。因此，对于风电场和抽水蓄能电站的发电成本主要从建设成本、运行维护成本和资金成本三个方面来考虑。

（1）建设成本

建设成本是建设风电场和抽水蓄能电站时的全部投资，包括建设前的勘测和设计等费用，建设中的施工费用和设备的购置安装等费用之和，用Uk表示。

（2）运行维护成本

运行维护成本包含了风电场和抽水蓄能电站为维持正常运行而每年所需的固定年费用和年运行费用。

固定年费用有建筑物和机电等设施的折旧费和大修提存费用，用Us表示，公式如下：

式中，Ul指电站经济寿命终了时的可回收成本；T为电站的经济寿命。

年运行费，指电站在运行期内所需的经常性维护费，包括厂用电费、抽水发电机组启停和工况转换费用，以及补水费等，记为Uy。

（3）资金成本

由于电站在初期投资建设时，只有少数的自有资金，其它大部分为商业贷款，因此应计及风电场和抽水蓄能电站在经济寿命期内每年应支付的利息和摊还的本金组成的资金成本，用Ud表示，公式如下：

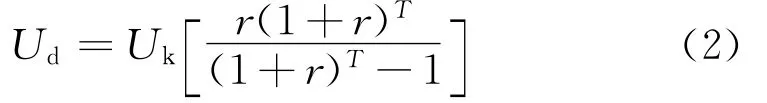
式中，r为折现率，一般按贷款利率取值。

综上，风电场和抽水蓄能电站的发电总成本Uac可表示为：

2 利润分配模型

2.1 利润分配原则

合理的利润分配不仅可以使所有者的合法权益得到保护，还可以保障合作长期稳定进行。风电-抽水蓄能电站合作联营的总利润受自然、社会等因素影响。只有将各因素考虑在内，才能尽可能地保证利润分配机制的合理性。本文主要考虑联营共同创造的总利润，以及风电场和抽水蓄能电站的贡献，分别介绍如下：

（1）联营获取的总利润

风电-抽水蓄能电站联合运营需要两者合理地做出机组组合调度，因此并网售电获得的总利润是共同创造的，应一同分享。

（2）联营中的贡献

风电-抽水蓄能电站联合运营关系达成之时，就形成了初步的利润分配方案。但是，风电场和抽水蓄能电站运行中，受自然条件等不确定影响频多，有可能导致风机倒塌或者水泵水轮机故障停机等事故发生。实际利润分配时考虑风电场和抽水蓄能电站对整个合作起到的贡献，以此可提高两者在维护设备等方面工作的积极性，既保证了合作联营的可靠性，又有助于增加收益。

2.2 利润分配的方法

合作博弈包含参与者集合N与特征函数v两个基本元素。令N＝｛1，2，…，i，…，n｝为有限参与者集合，其中i（1≤i≤n）为参与者的编号；集合N中的所有成员通过合作产生价值，记作v（θ）。用x（i）表示N中第i个成员从合作总利润中应得到的一份收益，则X＝｛x（1），x（2），…，x（n）｝称为合作博弈对策的分配策略。

目前解决合作利益分配问题的有效方法主要有均分策略、按容量分配策略、Shapely值法三种分配策略。

2.2.1 均分策略

均分策略下每位参与者平均分享联盟收益，风电-抽水蓄能电站合作组成的联盟中只有两个参与者，风电场w和抽水蓄能电站p，分别获得的利润x（w）和x（p）表示为：

式中，v（w，p）为合作后的整体利润。

2.2.2 按容量分配策略

该策略下，考虑每位参与者在合作中的贡献，收益与贡献成正比。

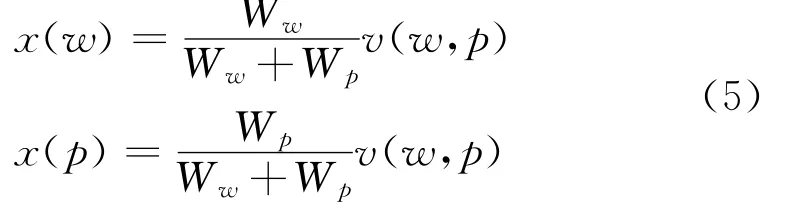
式中，Ww表示风电场在合作中贡献的电量，Wp表示抽水蓄能电站发出的电量。

2.2.3 Shapely值法

大规模风电场与抽水蓄能电站联合运营的前提是增加双方的收益，或者一方收益增加，另一方不受损害，整体收益大于每个成员单独经营时的收益［8］。合作能够产生一种合作剩余，可以借助于合作博弈理论研究风电-抽水蓄能联营企业的利润分配问题。

Shapely值法为每个参与者赋予唯一且易于量化计算的数值，表征其贡献，广泛用于多人合作博弈。风电-抽水蓄能电站组成的合作联盟满足对称性、有效性和累加性，因此可用Shapely值法进行利润分配。Shapely值法在合作博弈中存在唯一的单值解，满足个体理性和整体理性，第i位参与者分配得到的利润为：

式中，θ为联盟参与者的所有子集；|θ|为联盟θ中的参与者数目；N为联盟参与者的总数；r（θ）为联盟θ的加权因子。

因此，Shapely值法可看作博弈中的各可能联盟的边际贡献平均值，贡献大的参与者可以获得更多的利润。

3 算例仿真

3.1 并网收益

根据参考文献［9］中提到的风电-抽水蓄能电站联合优化运营模型，考虑风电场和抽水蓄能电站发电并网收入，以及抽水蓄能电站中水泵抽水的费用，让每天的效益最大化。算例结果分析中，计算出了当电网的功率限制为3～8 MW时，单独风电运行时的收益为每天113 060元，而风电和抽水蓄能电站联合运行时的日收入为119 180元。

参照文中给出的抽水蓄能电站的参数，当仅有抽水蓄能电站运行时，在每天的8点到22点时刻，上网电价较高时，把水库中可利用的储能全部用来发电上网，最大收入为：

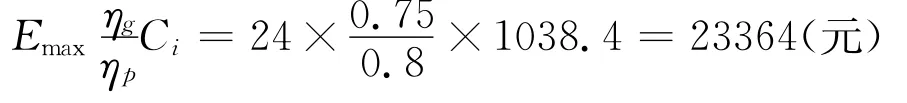
同样地，利用较低的电价，把水库的可利用储能达到最大值，消耗的抽水费用为：

因此，当抽水蓄能电站单独运行时，每天可获得的最大收益为：

3.2 运行成本

根据目前我国风力发电的实际情况，风电场建设期为1年，初期投资为8 000元／k W，年运行费用40元／k W，计划经济寿命为20年，残余价值为500元／k W，折现率r取值6%。

抽水蓄能电站的初期投资为1 600元／k W，计划经济寿命为50年，残余价值为200元／k W，折现率r取值6%。由于多余的风电补充了很大部分抽水费用，该模型中的抽水蓄能电站年运行费用为46元／k W。

文献［9］中的模型参数中，风电场和抽水蓄能电站的容量为12 MW，分别计算其每天的总成本结果如表1。

表1 电站每天的总成本

3.3 利润分配

3.3.1 均分时利润

均分策略下，风电场和抽水蓄能电站得到的利润为59 590元。

3.3.2 按容量分时利润

文献［9］中风电-抽水蓄能电站联合运营模式下，风电场每天的上网电量为150 MWh，抽水蓄能电站每天的上网电量为14.5 MWh。因此，按容量分配贡献分配利润时，风电场和抽水蓄能电站分别得到总利润的91.2%和8.8%。

3.3.3 Shapely值法时利润

根据上述Shapely值法分别分配风电场和抽水蓄能电站利润的计算方法如下：

（1）风电场的获利x（w）如表2。

表2 风电场利润计算

（2）抽水蓄能电站的获利x（p）如表3。

表3 抽水蓄能电站利润

综上，风电场与抽水蓄能电站在三种利润分配方法下，除去成本后，纯利润如表4。

表4 风电场和抽水蓄能在不同利益分配下的纯利润

如果按照均分策略来实现利润分配，抽水蓄能电站的收益多于风电场，显然不合理。如果按照容量分配策略来实现利润分配，虽然参与者都能实现盈利，但是抽水蓄能电站的净利润比风电场要大得多，这显然不利于两者的长期稳定合作。如果根据Shapely分配法来实现利益分配，很大程度上考虑了对联营的贡献，也可使两者的净利润大致均衡，这显然更有利于联盟的长期稳定运行。因此，Shapely方法更适合用于解决风电-抽水蓄能电站的利润分配问题。

4 结 论

本文通过分析计算风电场和抽水蓄能电站的运营成本、合作方式和每天盈利，讨论了不同的利润分配方法及相应的获利情况，最终确定了Shapely值法应用于该联营模式下的利润分配最为合理，体现了公平性，有助于激发两者的积极性和建立长期稳定的合作关系。

［1］ 陈允鹏.发展抽水蓄能电站是电网调峰和经济运行的选择［J］.中国能源，2005，27（8）：31-34.

［2］ 宋 豪，宋曙光，王 超，等.抽水蓄能电站对山东电网风电接纳能量的影响［J］.山东大学学报（工学版），2011，41（5）：138-142.

［3］ 朱建志.风电-抽水蓄能联合优化运行研究［D］.长沙：长沙理工大学，2013.

［4］ 胡泽春，丁华杰，孔 涛.风电-抽水蓄能联合日运行优化调度模型［J］.电力系统自动化，2012，36（2）：36-41.

［5］ 徐 飞，陈 磊，金和平，等.抽水蓄能电站与风电的联合优化运行建模及应用分析［J］.电力系统自动化，2013，37（1）：149-154.

［6］ 李 强，袁 越，李振杰，等.考虑峰谷电价的风电-抽水蓄能联合系统能量转换效益研究［J］.电网技术，2009，33（6）：13-17.

［7］ 曹 昉.风电及抽水蓄能电站容量规划方法研究［D］.保定：华北电力大学，2013.

［8］ 王莹莹，梅生伟，刘 峰.混合电力系统合作博弈规划的分配策略研究［J］.系统科学与数学，2012，32（4）：418-428.

［9］ 潘文霞，范永威，杨 威.风-水电联合优化运行分析［J］.太阳能学报，2008，29（1）：80-84.