两站测向交叉定位相对误差几何稀释度研究*

王国刚

(海军驻连云港七一六所军事代表室 连云港 222061)



两站测向交叉定位相对误差几何稀释度研究*

王国刚

(海军驻连云港七一六所军事代表室 连云港 222061)

针对工程中使用相对误差几何稀释度衡量定位精度的问题,论文以相对误差几何稀释度为研究对象,分析两站测向交叉定位原理,给出了传感器测角误差不同时,相对误差几何稀释度最小的传感器探测角度与测角误差关系,并讨论了传感器测角误差相同时,相对误差最小的平台最优布站方式。通过Matlab仿真,验证了传感器测角误差相同时结论的正确性。

交叉定位; 定位精度; GDOP; 相对误差; 最优布站

Class Number TN957

1 引言

与有源探测相比,无源探测不向目标发射电磁波,具有抗干扰性强,隐蔽性好和作用距离远的优点,随着测量技术、信息截获和处理技术的逐渐发展,无源探测在电子战系统中占据越来越重要的位置。常用的无源探测技术包括利用测量目标信号到达角度的测向交叉定位法和利用到达时间差的时差定位法,由于被动探测设备对目标的测量数据变化比较慢,变动范围比较小,因而方位信息是最可靠的辐射源参数之一。而大气波导情况比较复杂,俯仰角测量误差较大,所以只采用方位角进行定位相对稳定[1～3]。

测向网通常由若干个配置在不同位置的站台组成,每个探测平台可观测性有限很难独立实现对目标准确定位,往往设置多站进行联合测向,并由一个中心站接收数据在地图上进行交叉定位。根据工程需求,本文应用相对误差几何稀释度衡量定位精度,通过分析给出两被动雷达探测精度不同及相同条件下定位精度最高的条件,讨论探测精度相同时平台最优布置,使平台运动更加机动,增强平台布站的灵活性,对测向网合理优化配置研究具有重要意义。

2 两站测向交叉定位原理

设两个观测站的位置为(x1,y1)、(x2,y2),目标位置位于T(x,y)点,所测量得到的角度为θ1和θ2,两条方向的射线交于一点,该点即为目标的位置[4],如图1所示。

图1 两站测向交叉定位原理示意图

忽略两测向站坐标轴指向误差(即认为三个坐标轴分别平行),根据角度定义可得:

(1)

整理为

(2)

矩阵表示为

AX=Z

(3)

式中:

该算法忽略了地球曲率及两测向站坐标轴指向误差,两站距离较近时,误差较小可以忽略;但当两站距离较远时,误差较大,需进行相应的坐标变换修正[5]。

如果测量过程中没有误差,两站测向线在空间中交于一点,然而测量过程中总会存在误差,这些误差对位置估计的影响体现在方位线不再交于一点。如果测量误差是随机的,测得的方位角可能比实际方位角大,也可能比实际方位角小,从而形成一个误差椭圆。传感器中还可能存在测量偏差问题,即系统误差可以通过标校方法消除,因而随机测量误差对定位误差影响较大[6～9]。假定两站测角误差δθ1、δθ2服从均值为0的高斯分布,两站之间的测角误差相互独立。

分析测向定位误差,对式(2)求偏导,整理可得

(4)

写成矩阵形式为

AδX=B

(5)

其中:

故可以得:

δX=A-1B=T·B

(6)

令:

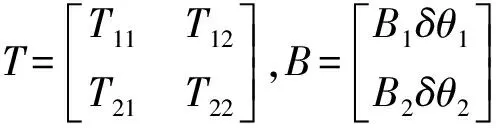
B1=(x-x1)sec2θ1,B2=(x-x2)sec2θ1

故式(6)又可写为

(7)

得到协方差矩阵为

(8)

其中:

3 相对误差几何稀释度分析

交叉定位算法的性能通常用误差几何稀释度(geometric dilution of precision,GDOP)来评估。GDOP是目标估计位置的均方根误差同量测均方根误差的比值,能够反映传感器与目标间的相对几何位置对量测误差的放大关系。这一方面表明传感器与目标间的相对几何位置能够对目标的估计位置产生影响;另一方面,不同的传感器与目标间的相对几何位置会产生不同的定位精度。因此,GDOP能够将各传感器与目标间的相对几何位置同定位精度联系在一起,并能够准确衡量前者对后者的影响程度。目前很多文献仅用目标位置的均方根误差表示GDOP。

通常有两种方式描述定位精度的GDOP曲线:二维平面内的等值线图及三维立体曲线,前者是后者在二维平面内的投影。一般等值线图描述GDOP的变化趋势,而立体图直观表示GDOP在整个观测区域内的总体结构。对于两站无源探测系统而言,GDOP三维立体曲线是在双站基线区域含有凸起且总体类似于马鞍面的结构,这些不能在二维等值线中得到反映[10]。

工程应用中,被动雷达常用相对误差几何稀释度ΔGDOP(%)作为指标衡量定位精度,即

(9)

(10)

根据:

代入式(10)可得:

(11)

式中:r1和r2分别为目标到两个测向站间的距离。

式(11)表明测向交叉的定位误差等于测向线交叉区域的多边形边长平方和除以其夹角的正弦,如图2所示。

假设两站的测角精度σθ=σθ1,σθ2=mσθ1,参考坐标系的原点选择为两个站A1,A2连线的上O,x轴为两个站连线方向,y轴符合右手法则。

图2 测向交叉定位误差区域示意图

图3 测向交叉定位示意图

将式(11)简化得:

(12)

由于

(13)

式中:R为目标到达两个测向站基线的距离。

将式(13)代入式(12)中可得:

(14)

则:

(15)

由式(15)可知,相对误差几何稀释度与传感器的精度、平台布站方式等有关。

4 相对误差几何稀释度与布站关系分析

为了便于分析,令:

(16)

比较式(15)和式(16),可知ω与ΔGDOP具有相同的单调性,并且当ω取最小值时,ΔGDOP也取最小值[11]。

(17)

(18)

式中:

α=(θ1-θ2)

如果在某一个θ1和θ2取得最小值,必然满足以下极值条件:

(19)

则:

(20)

以0≤θ1≤π/2为例,因为辐射源目标不在基线或延长线上,所以θ1≠θ2且θ1≠0,θ2≠0。

(21)

整理得:

(22)

式(22)为两传感器探测误差不同时相对误差几何稀释度最小的条件。由于式(22)无法得出平台布站与探测角的直接关系,因此讨论m=1,即两平台探测误差相等σθ=σθ1=σθ2时相对误差几何稀释度与平台布站关系。

当θ1=π-θ2,两条测向线交叉成为一个等腰三角形,交点在y轴上,则最优的定位精度在x=0处获得。

设两站连线中心为原点,目标位于两站连线的中间位置,θ1=π-θ2=θ,代入式(15)中可得:

(23)

当sin2θcosθ取得最大值时,ΔGDOP取得最小值。sin2θcosθ对于θ求导并令其等于0,可得

(24)

故目标位于两站连线的中间位置,且与两站夹角约为70.6°时,测向交叉定位的相对误差几何稀释度最小。

5 仿真验证与分析

为了验证两站传感器探测误差相同时,相对误差几何稀释度最小条件,仿真实验设置目标位于两探测平台中线上,与基线距离29km,平台以10m/s的速度从(300km,0)运动至(0km,0),方位探测误差为1°,则交叉定位角与相对误差几何稀释度关系如图4所示。

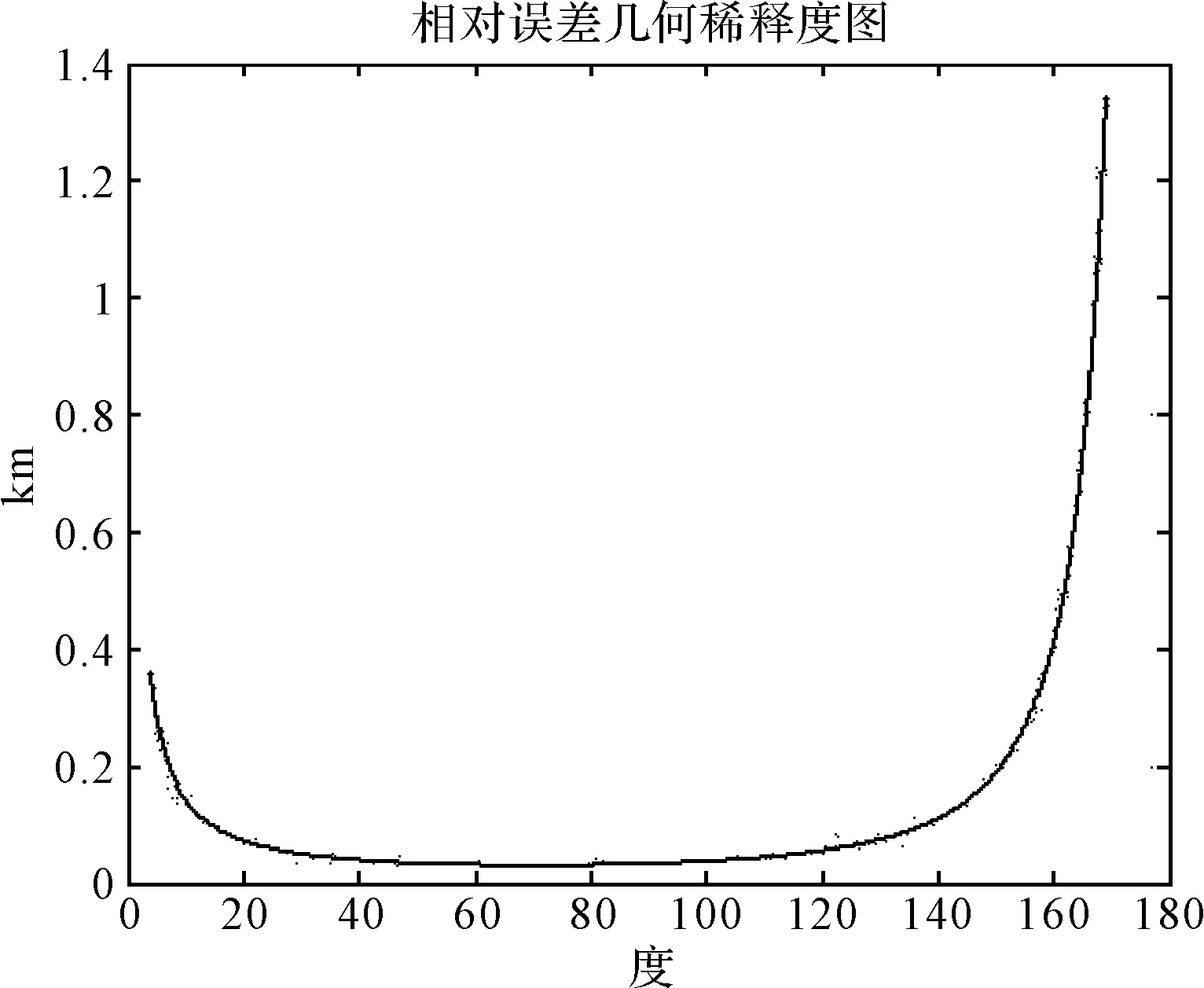
图4 方位探测误差1度时定位角与ΔGDOP关系图

由图4可以看出,当目标位于两探测平台中间位置,交叉定位角0°～20°时,ΔGDOP递减,在30°～110°间ΔGDOP变化平缓,大约70°时,ΔGDOP最小。当交叉定位角大于120°时,即辐射源目标靠近基线时,ΔGDOP增大。

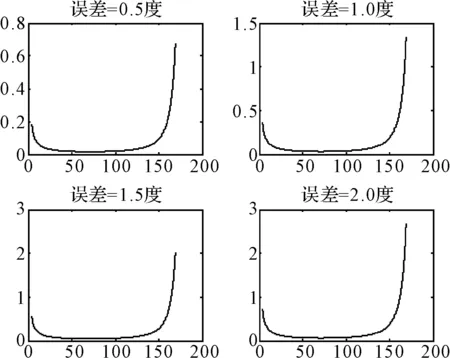
图5 方位探测误差不同时定位角与ΔGDOP关系图

考虑到传感器探测误差大小对ΔGDOP的影响,仿真实验设置目标位于两探测平台中线上,与基线距离29km,平台以10m/s的速度从(300km,0)运动至(0km,0),方位探测误差分别为0.5°、1.0°、1.5°、2.0°时交叉定位角与相对误差几何稀释度ΔGDOP关系如图5所示。

由图5可以看出,随着方位探测误差增大,ΔGDOP值增大。虽然方位探测误差不同,但随着交叉定位角增大,ΔGDOP呈先减后增趋势,当交叉角大约70°时,ΔGDOP最小。当辐射源目标在基线位置时,ΔGDOP最大。

6 结语

本文在工程中使用相对误差几何稀释度衡量定位精度的需求下,详细阐述了两站测向交叉定位原理并分析相对误差几何稀释度,给出传感器探测误差相同和不同时相对误差最小条件及传感器探测误差相同时平台最优布站方式。仿真实验表明方位探测误差越大,相对误差几何稀释度越大,同时传感器探测误差相同,辐射源目标位于两站连线的中间位置,且与两站夹角约为70.6°时,定位的相对误差几何稀释度最小。本文研究用于两观测站对辐射源目标测向定位时,指导平台相对目标合理机动提高定位精度,为辅助指挥员生成协同探测方案提供理论和技术支撑。

[1] Levanon N. 2D条件下的最小GDOP[J]. IEEE Proc.雷达,声纳,2000,147(3):149-155.

[2] Ivan K.传感器融合最优几何布置[C]//SPIE会议信号处理部分,传感器融合与目标识别,Florida,1998:74-78.

[3] Torrieri D J.被动定位系统统计理论[J]. IEEE Trans on AES,1984,AES-20(2):183-197.

[4] 孙立杰,马中,陈世友,等.无源交叉定位算法的原理误差比较与分析[C]//第四届信息融合大会论文集,2012:163-166.

[5] 修建娟,何友,王国宏,等.测向交叉定位系统中的交会角研究[J].宇航学报,2005,26(3):282-286.

[6] Richard A. Poisel.电子战目标定位方法[M].北京:电子工业出版社,2008:167-168.

[7] 周亦军,李旻,李锐.纯方位定位中观测站布局优化研究[J].舰船电子工程,2010,30(11):69-71.

[8] 刘忠.纯方位目标运动分析[M].北京:国防工业出版社,2009:56-66.

[9] 王本才,王国宏,何友.多站纯方位无源定位算法研究进展[J].电光与控制,2012,19(5):56-60.

[10] 李兴民,李国君,李健,等.双站交叉定位雷达布站方法研究[J].雷达科学与技术,2011,9(5):405-408.

Relative Geometric Dilution of Precision in Double Station Bearing-only Location

WANG Guogang

(Navy Representative Office in 716 Research Institute in Lianyungang, Lianyungang 222061)

According to the positioning accuracy measured by the relative GDOP in engineering, the paper takes the relative GDOP as the research project and analyzes the double station bearing-only principle. Adopting the minimum relative GDOP as prerequisite, the paper deduces the relationship of the sensor detection angle and angle error on the condition of different angle errors, discusses the optimal placement of the platform on the condition of the same angle errors. Further on, the Matlab simulation result verifies the conclusion on the condition of the same angle errors.

bearing-only, positioning accuracy, GDOP, relative error, optimal placement

2015年6月3日,

2015年7月26日

王国刚,男,工程师,研究方向:作战系统试验评估方法。

TN957

10.3969/j.issn.1672-9730.2015.12.016