一种水下高速小目标的多普勒频率估计方法*
孙常存 邢国强 曲兆宇
(91439部队 旅顺 116041)
一种水下高速小目标的多普勒频率估计方法*
孙常存 邢国强 曲兆宇
(91439部队 旅顺 116041)
针对近程主动声探测水下高速小目标的回波多普勒频率估计问题,根据ESPRIT算法原理,提出了一种改进的ESPRIT频率估计算法。该算法利用目标回波信号的时延数据,构造两组完全相同的子阵列,通过对两组子阵列的互协方差矩阵构造的矩阵束进行广义特征分解,实现了对水下高速小目标回波信号的多普勒频率估计。与标准ESPRIT算法相比,改进的ESPRIT算法不需要进行自协方差矩阵的特征分解,因而具有较低的计算复杂度。计算机仿真表明,该方法对水下高速小目标的回波多普勒频率估计是有效的。
高速小目标; 主动探测; ESPRIT; 特征分解; 多普勒频率; 估计算法
Class Number TN911.7
1 引言
水下高速小目标近程主动声探测技术是水声技术的一个重要研究领域,文献[1~3]围绕该问题进行了相关的研究,其中,目标回波的多普勒频率估计是实现目标有效探测的前提条件。由于目标速度高,近程探测的工作时间短,且频率估计精度直接影响到目标速度、距离等相关参数的估计精度,因此分辨力和实时性是水下高速小目标多普勒频率估计应用中的两项关键技术。因此,必须针对高速小目标近程探测的特点,研究目标回波的多普勒频率估计问题,实现对高速小目标回波多普勒频率的快速精确估计。
频率估计的方法主要有经典法和现代法两大类[4],经典法由于快速傅立叶变换(FFT)的提出而极大地减小了运算量[5],但由于其分辨力低而在应用中受到了限制;现代法中具有代表性的是基于特征分解的MUSIC法[6],理论上具有无限的分辨力,但该法需要进行参数空间搜索,运算量较大,实时性差制约了其在工程中的应用。子空间旋转不变法即ESPRIT法是80年代末Roy R提出的一种新方法[7],由于其不需作扫描处理,因而在保证精度的基础上极大地减少了运算量,增加了工程适用性。本文根据ESPRIT原理[8],提出一种改进的ESPRIT算法,并通过仿真实验证明该方法应用于水下高速小目标回波多普勒频率估计的有效性。
2 目标回波数据模型
假定目标回波信号与噪声都是零均值平稳随机过程,信号包含K个频率分量,且信号之间互不相关,加性噪声是互不相关且独立于源信号的高斯白噪声,则接收传感器输出数据的离散形式为
(1)
式中,sk、fk分别为第k(k=1,2,…,K)个谐波信号的幅值和频率;w(n)表示输出的加性高斯白噪声。构造如下N维数据向量:
(2)
可表示为矩阵形式:
X(n)=BS(n)+W(n)
(3)
式中
B=[b(f1),b(f2),…,b(fK)]N×K
b(fi)=[1,ej2πfi,…,ej2πfi(N-1)]T,i=1,2,…,K
S(n)=[s1ej2πnf1,s2ej2πnf2,…,sKej2πnfK]T
3 改进的ESPRIT算法
ESPRIT算法原理可参阅文献[9],由于要利用两个对称子阵的自协方差矩阵和互协方差矩阵的广义特征分解来实现频率估计,因此标准ESPRIT算法的运算复杂度较高,且其主要运算量在于自协方差矩阵的特征分解,约占算法总运算量的96%(阶数为6,数据长度100)。为了进一步降低标准ESPRIT算法的运算复杂度,提出一种改进的ESPRIT频率估计算法,算法的基本原理是,利用目标回波信号的时延数据,构造两组完全相同的子阵列,通过对两组子阵列的互协方差矩阵构造的矩阵束进行广义特征分解直接估计出谐波频率分量,具体算法如下:
1) 对信号进行M=2N点采样,由采样数据x(n)构造两个N维对称子阵X(n)和Y(n):
X(n)=[x(n),x(n+1),…,x(n+N-1)]T
(4)
为了获得两个相同的子阵,将X(n)延时NTs(Ts为抽样间隔),得到Y(n):
Y(n)=[x(n+N),x(n+N+1),…,x(n+2N-1)]T
(5)
同样可表示为矩阵形式:
X(n)=BS(n)+W(n)
(6)
Y(n)=X(n+N)=BΦS(n)+W(n+N)
(7)
式中,Φ=diag(ej2πf1N,ej2πf2N,…,ej2πfKN),即为旋转不变对角阵,其每一个对角元素都与频率有关,称为频率因子。由于Φ为酉矩阵,所以X(n)和Y(n)具有相同的观测空间(信号子空间和噪声子空间)。
2) 计算p维的互协方差矩阵RXY和RYX
由式(6)和式(7)可得出X(n)和Y(n)的空间互协方差矩阵为RXY=E[X(n)Y(n)H]
=BSΦHBH+E[BS(n)W(n+N)H]
+E[W(n)S(n)HΦHBH]+E[W(n)W(n+N)H]
(8)
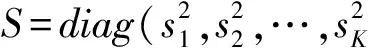
RXY=BSΦHBH
(9)
同理可得:
RYX=E[Y(n)X(n)H]=BΦSBH=RXYH
(10)
3) 构造矩阵束(RYX,RXY),通过求其广义特征值,估计出所有谐波频率分量
由式(9)和式(10)构造矩阵束(RYX,RXY)为
RYX-λRXY=BS(Φ-λΦH)BH
(11)
由于B列满秩,对角阵S非奇异,当λ≠ej4πfiN(i=1,2,…,K)时,由矩阵的性质知:
rank(RYX-λRXY)=rank(Φ-λΦH)=K
(12)
当λ=ej4πfiN(i=1,2,…,K)时,对角阵Φ-λΦH的第i行元素全部为零,同时矩阵RYX-λRXY的秩降为K-1,所以λ=ej4πfiN(i=1,2,…,K)是矩阵束(RYX,RXY)的广义特征值。可见,通过对矩阵束(RYX,RXY)进行广义特征分解,得到其广义特征值ej4πfiN(i=1,2,…,K),即可估计出所有谐波频率分量fi(i=1,2,…,K)。由于该方法避免了标准ESPRIT算法中自协方差矩阵的特征分解,因而运算量大为减小。
4 计算机仿真
考虑式(1)的离散数据模型,仿真中,回波信号采用以下数学模型:
x(t)=Acos(2πfdt)+e(t)
(13)
式中,fd为多普勒频率,根据近程主动探测高速小目标的实际情况,取为10kHz;e(t)为均值为0、方差σ2=1的高斯白噪声,信噪比定义为SNR=10lg(A2/2σ2)。根据奈奎斯特采样定理,取采样频率fs=200kHz,发射脉冲信号宽度T=1ms,则每个回波采样点数M=2N=200。
仿真1:为了验证协方差矩阵维数p对频率估计精度的影响,选取SNR=10dB,M=200,对回波信号进行300次蒙特卡洛仿真实验,频率估计结果见表1。仿真结果表明,协方差矩阵维数p对频率估计精度影响不大。随着维数的增加,估计的标准差略有减少,对于单频信号,p值可减至4。
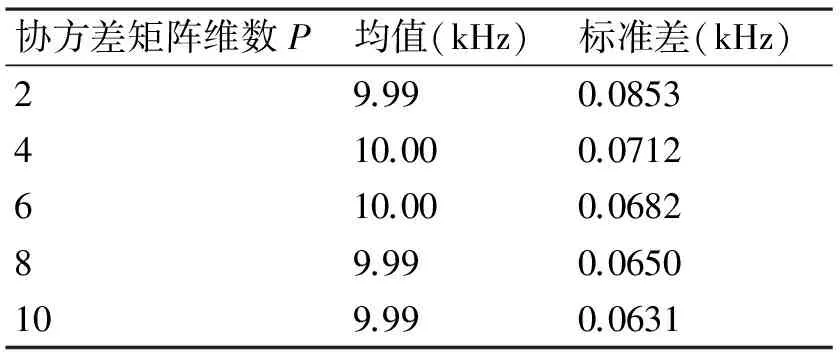
表1 不同协方差矩阵维数时频率估计结果(SNR=10dB,M=200)
仿真2:为了说明改进的ESPRIT算法在不同数据长度下的频率估计性能,选取SNR=10dB,p=4,对不同数据长度下的回波信号进行300次蒙特卡洛仿真实验,频率估计结果见表2。由文献[10]知,实正弦信号无偏频率估计的Cramer-Rao下界可表示为
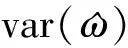
(14)
即:
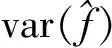
(15)
图1给出了表2情况下,频率估计标准差(Standard Deviation,SD)随数据长度变化的曲线及其Cramer-Rao界。仿真结果表明,数据长度M对频率估计精度及估计的标准差均有影响,随着M取值的增大,其标准差将逐渐接近CRB,当M取200时,频率估计结果可以满足要求。

表2 不同数据长度时频率估计结果(SNR=10dB,p=4)
仿真3:为了说明本文方法在不同信噪比条件下的频率估计性能,选取M=200,p=4,对不同信噪比条件下的回波信号进行300次蒙特卡洛仿真实验,频率估计结果见表3。同样给出频率估计标准差随信噪比的变化曲线及其Cramer-Rao界,如图2所示。仿真结果表明,随着信噪比的增加,频率估计的标准差逐渐接近CRB,表明算法对回波信号多普勒频率估计是适用和有效的。特别是SNR>10dB时,频率估计的标准差非常接近CRB。
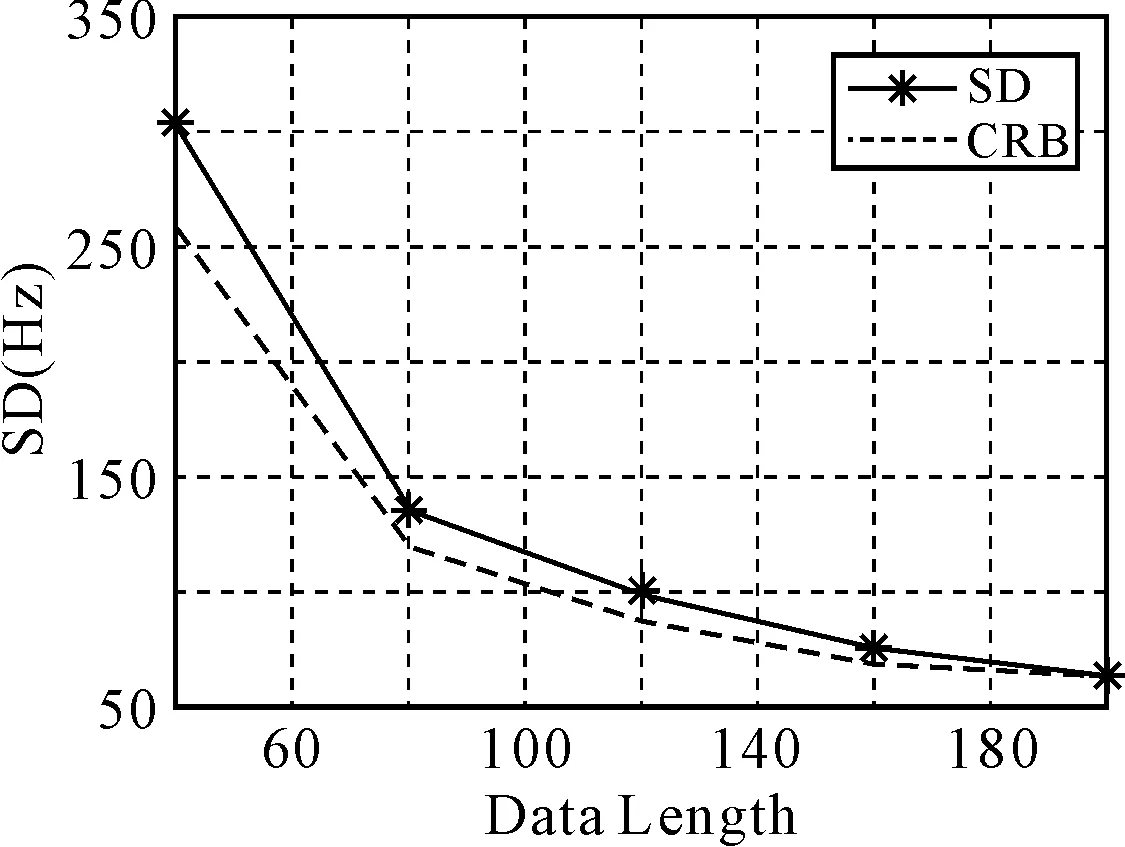
图1 频率估计标准差随数据长度变化曲线
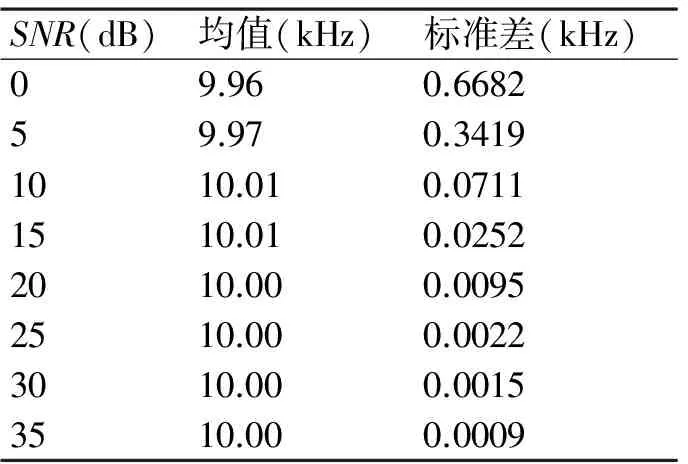
SNR(dB)均值(kHz)标准差(kHz)09.960.668259.970.34191010.010.07111510.010.02522010.000.00952510.000.00223010.000.00153510.000.0009
由以上仿真结果得出:改进的ESPRIT算法的频率估计具有较好的无偏性,其频率估计精度主要取决于信号的信噪比。通常情况下,高分辨率方法要求输入信号信噪比较高,约为10dB~15dB。对于单频信号,由于不存在相邻频率分辨的问题,对其信噪比的要求有所降低。对于水下高速小目标的主动声探测,接收回波的信噪比SNR≈0dB。若声探测系统为全向接收,其空间处理增益为零,系统检测过程中的窄带滤波滤除了噪声从而增加了信噪比,加上系统的时间处理增益,接收系统输出信号信噪比可达到10dB以上。因此,改进的ESPRIT算法频率估计具有较高的精度。
5 结语
本文针对近程主动声探测水下高速小目标的回波多普勒频率估计问题,提出了一种改进的ESPRIT频率估计算法。该方法与标准ESPRIT算法频率估计的不同之处在于不需要对自协方差矩阵进行特征分解,因而在保证精度的基础上运算量大为减小,可以满足实时性的要求。计算机仿真表明,改进的ESPRIT算法的频率估计具有较好的无偏性,其频率估计精度主要取决于信号的信噪比。该算法对水下高速小目标的回波多普勒频率估计是有效的。
[1] 杨崇林,陆善明,姚蓝.水下动目标近程主动声引信技术研究[J].中国造船,2000,41(4):71-82.
[2] 王琳,陆善明,刘平香.高速小目标探测中的信号处理技术[J].声学技术,2004,23(z1):296-301.
[3] 杨崇林,姚蓝.水下高速小目标探测中的信号波形设计研究[J].声学学报,2001,26(5):389-394.
[4] 冯晋利,李斌,李志舜.高分辨频率估计的数字信号处理系统设计[J].数据采集与处理,1999,14(2):234-237.
[5] 白小舒,袁嗣杰.基于FFT的雷达多普勒频率快速估计方法[J].装备指挥技术学院学报,2003,14(6):68-70.
[6] 石要武,戴逸松,丁宏.有色噪声背景下正弦信号频率估计的互谱Pisarenko和MUSIC法[J].电子学报,1996(10):46-50.
[7] 窦慧晶,王树勋,汪飞.二维正弦信号频率估计的ESPRIT方法研究[J].吉林大学学报(信息科学版),2005,23(2):123-128.
[8] 葛利嘉,陈天麒.利用旋转不变技术实现方向/频率联合估计[J].电子学报,1996,24(12):32-35.
[9] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE ASSP,1989,37(7):984-995.
[10] 阎振华,黄建国,韩晶.改进的低信噪比短序列快速频率估计算法[J].系统工程与电子技术,2009,31(8):1990-1992.
Doppler Frequency Estimation Method of Underwater High-Speed Small Target
SUN Changcun XING Guoqiang QU Zhaoyu
(No. 91439 Troops of PLA, Lvshun 116041)
Aiming at the problem of estimating doppler frequency of underwater high-speed small target, based on the principle of ESPRIT algorithm, an improved ESPRIT algorithm is put forward. By the time delay data of target echo signal, two sub-arrays with the same array shape are constructed. A matrix pencil is constructed by the cross covariance matrix of the two sub-arrays. By means of generalized eigen-decomposition of the matrix pencil, the doppler frequency of underwater high-speed small target can be obtained. Compared with standard ESPRIT algorithm, the improved ESPRIT algorithm does not need to do eigen-decomposition of auto-covariance matrix, thus has lower computational complexity. The simulation results show that the proposed method is effective for estimating doppler frequency of underwater high-speed small target.
high-speed small target, active detection, ESPRIT, eigen-decomposition, doppler frequency, estimation algorithm
2015年4月20日,
2015年5月31日
孙常存,男,博士,工程师,研究方向:鱼雷自导与引信技术。
TN911.7
10.3969/j.issn.1672-9730.2015.10.041

