系统误差情况下两坐标雷达目标高度可观测分析*

龚 诚 崔亚奇 刘思琪

(1.91049部队 北京 100000)(2.海军航空工程学院信息融合研究所 烟台 264001) (3.张家口职业技术学院电气工程系 张家口 075000)



系统误差情况下两坐标雷达目标高度可观测分析*

龚 诚1崔亚奇2刘思琪3

(1.91049部队 北京 100000)(2.海军航空工程学院信息融合研究所 烟台 264001) (3.张家口职业技术学院电气工程系 张家口 075000)

针对雷达普遍存在距离和角度量测系统误差工程实际情况,以及现有两坐标雷达目标高度可观测分析和估计技术缺乏对雷达系统误差考虑不足之处,论文利用Fisher信息矩阵,通过求解CRLB下限,对系统误差下的两坐标雷达目标高度可观测分析问题进行了深入研究,并通过数值仿真,对系统误差、雷达配置对目标高度可观测的影响以及目标高度估计精度等问题进行了分析,给出了有用结论,为后续系统误差情况下目标高度估计提供了指导。

雷达组网; 系统误差; CRLB; 目标高度估计

Class Number TP953; TN957

1 引言

在目标运动分析(Target Moving Analysis,TMA)中,目标的状态估计可通过随时间变化的测量而得到。在由两坐标雷达组成的雷达网中,雷达所能提供的测量是距离和方位角。由于两坐标雷达观测的不完整性,因此,可以通过把多个两坐标雷达的观测综合起来以改善目标状态的可观测性。

在利用多部两坐标雷达量测对目标高度进行组网估计前,需要对目标高度的可观测性进行理论分析,以确保有的放矢。文献[3]推导了目标高度估计误差的克拉美-罗下限(Cramer-Rao low bound,CRLB)下限,并通过不同条件下的数值计算证明了:目标高度估计误差的CRLB既与雷达的测角误差有关,也与目标和两个雷达站形成的夹角有关系;雷达配置在不同的高度上有利于目标高度估计的收敛性。这些结论对于两坐标雷达组网以及雷达网中的传感器管理具有指导意义。在文献[3]理论分析的指导下,出现了多种目标高度估计优化算法。

在雷达实际系统中,由于雷达内部线路延时、系统零点漂移、距离时钟速率、雷达天线对准正北不准确等不可消除因素的存在,导致雷达存在距离和角度系统误差,然而现有的两坐标雷达目标高度估计方法对此并没有明确考虑,致使所研算法在实际运用过程中目标高度估计不准确不稳定。因此很有必要针对实际工程需要,对系统误差存在情况下的两坐标雷达目标高度估计问题进行研究,并首要对系统误差存在情况下两坐标雷达目标高度的可观测性问题进行研究。

基于上述分析,论文对系统误差情况下目标高度的可观测性进行研究,首先通过公式推导,求解目标高度的CRLB下限,然后通过数值计算,对目标高度的可观测性进行分析,并得出一些有用的结论。

2 系统建模

假定在雷达网中有三个两坐标雷达,它们提供目标的距离和方位角,且雷达的量测包含系统误差,目标位于(x,y,z)处,雷达i位于(xoi,yoi,zoi)处,ri和βi是目标相对于雷达i的距离和方位角真值,rmi和βmi是雷达i(i=1,2,3)测量得到的目标距离和方位值,包含系统误差和随机噪声误差,其中系统误差为bri和bθi,并假设其是慢变的,可认为是恒值常量,另假定随机噪声误差是独立、零均值高斯分布的,σri和σβi,i=1,2,3,是雷达i的测距和测角标准差。

令

X=(x,y,z)T(x1,x2,x3)T

(1)

b=(br1,bθ1,br2,bθ2,br3,bθ3)T

(2)

z=(rm1,βm1,rm2,βm2,rm3,βm3)T(z1,z2,z3,z4,z5,z6)T

(3)

则测量方程可表示为

(4)

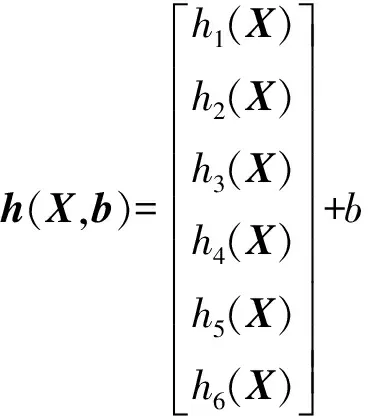
(5)

(6)

于是,向量X的似然函数可表示为

(7)

令Y=[XT,bT]T

L=-lnp(Z|X,b)

(8)

3 CRLB下限推导

下面利用Fisher信息阵(FIM),对系统误差情况下两坐标雷达目标高度信息的可观测性进行分析。

根据FIM的定义可得

(9)

根据矩阵求导公式

(10)

由方程(8)和方程(10)可得

(11)

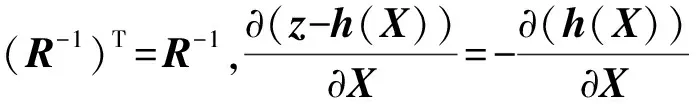
(12)

进而可得

(13)

(14)

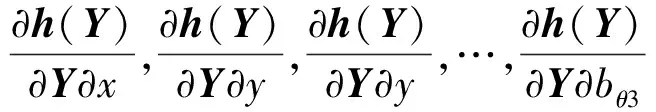
(15)

(16)

其中

(17)

(18)

(19)

于是,目标位置和雷达系统误差估计误差的CRLB为

CRLB(X)=I-1

(20)

4 数值分析

下面通过仿真对目标高度和雷达系统误差的可观测性进行仿真分析。

假设系统存在三部雷达,其位置分别为(-Lm,0m,0m,)、(Lm,0m,0m,)、(0m,Lm,0m,),目标高度为5000m,雷达量测协方差为R=diag(100,0.0175,100,0.0175,100,0.0175)2,目标位置和雷达系统误差的初始信息为I0=diag(1/2.5e7,1/2.5e7,1/2.5e7,1/4e4,2.5e3,1/4e4,2.5e3,1/4e4,2.5e3)。雷达对目标高度估计、系统误差的估计误差的几何分布如图1～图5所示。

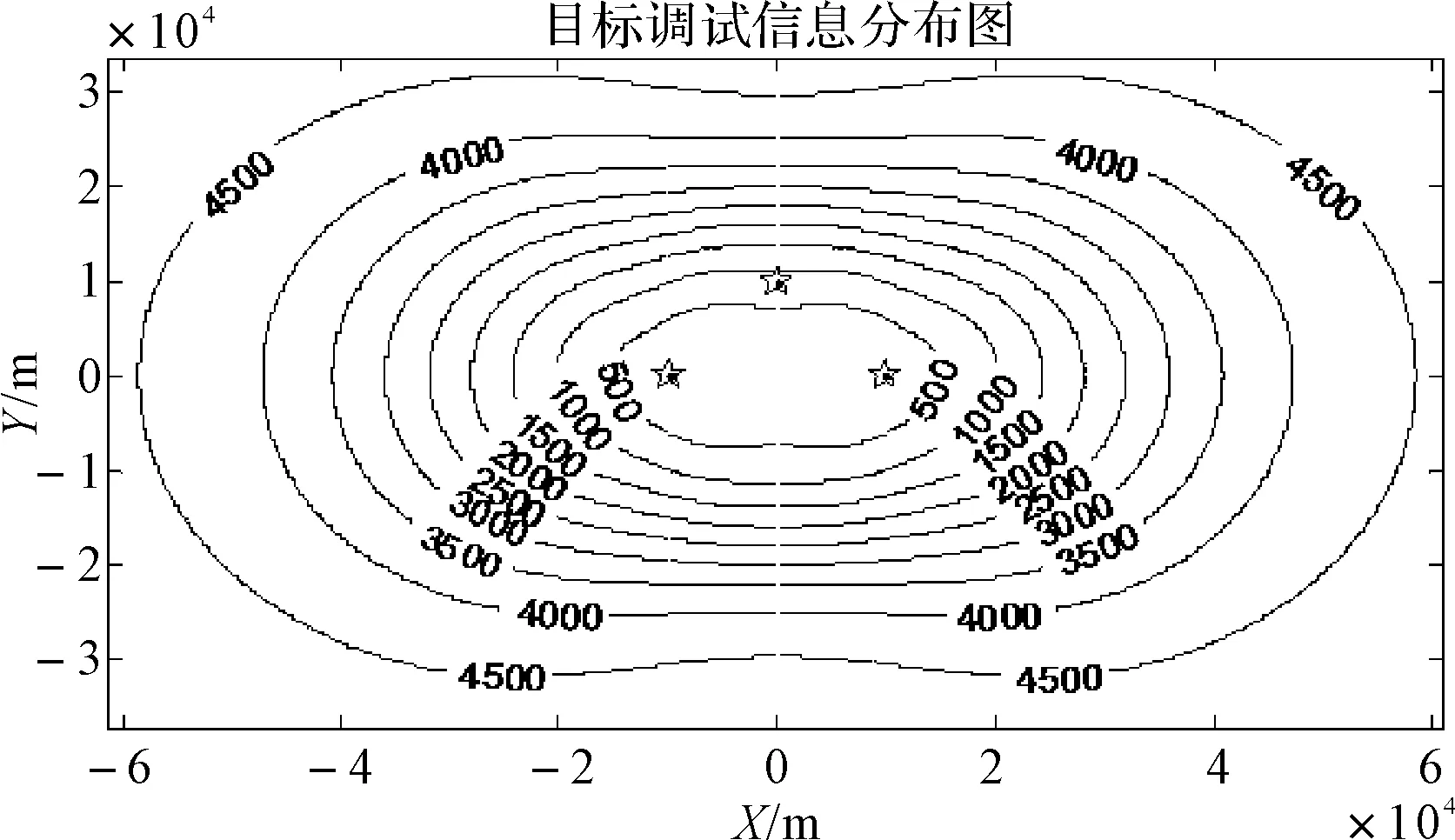
图1 目标高度估计误差的几何分布(等高线单位:m)

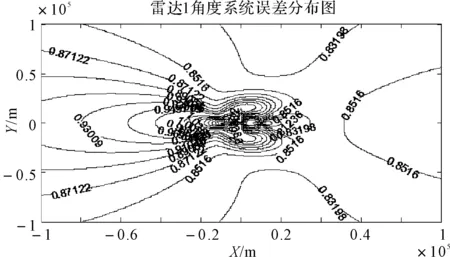
图3 雷达1测角系统误差估计误差的几何分布(等高线单位:°)

图4 雷达2测距系统误差估计误差的几何分布(等高线单位:m)

图5 雷达3测角系统误差估计误差的几何分布(等高线单位:°)

对比文献[3]结果可知,即使通过三部雷达对目标的高度进行估计,其估计效果也差于无系统误差同等配置的两部雷达的结果,因此系统误差的存在对目标高度的估计具有很大的影响。

由图2～图5可知,雷达测距系统误差的估计下限大致为150m,而实际系统雷达一般具有1000m左右的测距系统误差,因此通过联合估计的方式,估计出的结果还是基本满足要求的,但测角系统误差的估计下限大致为1°左右,而实际雷达一般具有2°左右的测角系统误差,因此测角系统误差的估计很难满足实际的需求。并且目标高度和系统误差的估计误差呈相反的分布,很难使它们同时达到最优,因此通过联合估计的方式对目标位置和系统误差进行同时定位,很难对目标进行有效地定位。

通过上面的分析可知,在雷达存在系统误差的情况下,要对目标高度进行有效定位,雷达系统误差进行有效估计,对它们进行联合估计是不可行的,唯一的办法是把它们物理分开,分别建立模型进行估计。

5 结语

论文考虑到雷达普遍存在距离和角度量测系统误差工程实际情况,针对现有两坐标雷达目标高度可观测分析以及估计理论不足之处,利用Fisher信息矩阵,对系统误差下的坐标雷达目标高度可观测分析问题进行了分析研究,并依据分析结果,对实际雷达组网目标高度估计问题给出了相应的建议。

基于论文分析结果,后续将进一步对系统误差情况下的两坐标雷达目标高度估计技术进行研究。

[1] 谢俊好,李波.T/R-R高频地波雷达球面定位算法研究[J].电子学报,2012(3):435-440.

[2] 雷雨,冯新嘉,朱灿彬,等.2D雷达情报组网目标高度估计[J].火力与指挥控制,2011(12):157-159.

[3] 王国宏,许建逢,毛士艺,等.2D雷达组网目标高度估计误差的Cramér-Rao限[J].航空学报,2004(1):66-68.

[4] 赵孔瑞,周共健,于长军,等.高频地波雷达飞行目标高度估计[J].系统工程与电子技术,2012(8):1571-1575.

[5] 张硕,金永镐,于长军,等.高频地波雷达目标高度估计起始的HPEKF算法[J].哈尔滨工业大学学报,2007(5):725-729.

[6] 游伟,何子述,胡进峰.基于匹配场处理的天波雷达高度估计算法[J].电子与信息学报,2013(2):401-405.

[7] Rakvongthai Y, Jifeng R, Rivananthan S, et al. Altitude estimation for 3-D tracking with two 2-D radars[C].2011.

[8] Poullin D, Flecheux M. Passive 3D tracking of low altitde targets using DVB(SFN Broadcasters)[J]. Aerospace and Electronic Systems Magazine, IEEE,2012,27(11):36-41.

[9] Jing S, She S, Jia-Dong X. 3D shape reconstruction from 2D ISAR measurements[C]. 2012.

[10] Rosebrock J. Absolute Attitude From Monostatic Radar Measurements of Rotating Objects[J]. Geoscience and Remote Sensing, IEEE Transactions on,2011,49(10):3737-3744.

Observability Analysis of Height Estimation in 2D Radar Network with Systematic Biases

GONG Cheng1CUI Yaqi2LIU Siqi3

(1. No. 91049 Troops of PLA, Beijing 100000) (2. Research Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001) (3. Electrical Engineering Department, Zhangjiakou Vocational and Technical Institute, Zhangjiakou 075000)

According to the actual condition of the 2D radar measurements about range and azimuth general contain systematic biases, and aiming to the deficiencies of the existing observability analysis method and estimation technology which don’t take radar systematic biases into account, the paper deeply researches the observability analysis problem about 2D radar height estimation when considering systematic biases through solving CRLB by Fisher information matrix. The problems that the influence of systematic biases and radar disposition on the target height observability and the estimation accuracy of target height are analyzed by simulation. The useful conclusions are drawn, which can offer guidance to the height estimation in conditions of systematic biases.

radar network, systematic biases, CRLB, estimation of target height

2015年4月3日,

2015年5月27日

龚诚,男,工程师,研究方向:情报处理。崔亚奇,男,博士,讲师,研究方向:数据处理、效能评估。刘思琪,女,工程师,研究方向:数据处理、自动化。

TP953; TN957

10.3969/j.issn.1672-9730.2015.10.019