机器人多指手抓取爆炸物能力研究*

莫海军 林志生

（华南理工大学机械与汽车工程学院，广东 广州 510640）

机器人多指手抓取爆炸物能力研究*

莫海军 林志生

（华南理工大学机械与汽车工程学院，广东 广州 510640）

应用力螺旋理论建立了多指手抓取矩阵与外力螺旋之间的关系，对多指手抓取爆炸物能力进行研究.首先建立多指手抓取爆炸物的力学模型，确定影响抓取的参数；然后以最大抓取重量为目标函数，建立满足力封闭约束条件下的抓取数学模型，并采用神经网络和优化方法对多指手抓取爆炸物进行了仿真，研究多指手不同抓取位置与爆炸物重量之间的对应关系，获得了多指手抓取爆炸物时最有利的抓取位置.

机器人多指手；抓取能力；神经网络；爆炸物

长期以来，排爆机器人处理爆炸物是通过操作执行器来进行的，只能完成简单的夹持动作，对于有危险性的爆炸物不能进行精细的操作，而且，在夹持的时候也无法判断夹持力的大小，过大或过小的夹持力都会导致抓取爆炸物的稳定性问题，甚至会发生爆炸.将具有多自由度的高灵活性的多指手应用到排爆机器人中进行排爆作业，不仅可改善夹持器简单的夹持功能，而且可以完成对爆炸物的精细操作和夹持力精确控制，这样不仅可提高机器人对爆炸物的处理能力，而且也极大地提高了排爆机器人操作的安全性［1-2］.

当多指手抓取爆炸物时，手指的接触力与爆炸物的重量及抓取位置之间存在一定的映射关系［2-4］，亦即不同的抓取位置对应于不同的抓取模式.本研究以爆炸物为抓取对象，以多指手抓取最大重量为目标函数，运用优化方法建立在满足力封闭约束条件下的数学模型，并用神经网络方法获得抓取位置与爆炸物重量之间的关系，为多指手抓取易爆危险品提供理论依据.

1 多指手抓取模型

图1为m个手指的多指手抓取任意形状物体的抓取模型，接触点分别为k1、k2、k3…、km.物体在接触点受到手指指尖施加的力称为接触力，用ftip表示为：

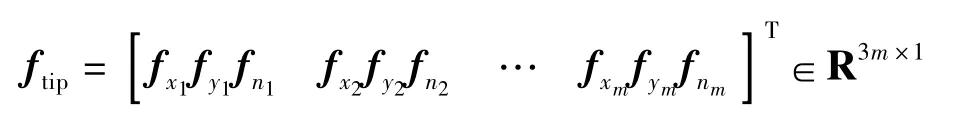
式中：fxi、fyi（i=1，…，m）分别为手指与爆炸物接触点的切向力，即摩擦力；fni为接触点的法向力，方向指向爆炸物内表面，并垂直于接触表面，显然fni≥0.

因此，接触力可分为切向力和法向力.

另外，接触点的切向力与法向力应当满足摩擦力约束条件：

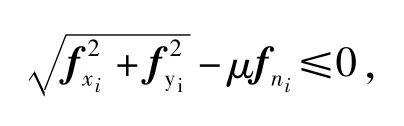
其中，μ为摩擦系数.

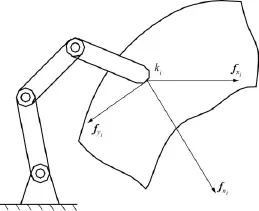
图1 多指手抓取模型Fig.1 Graspingmodelwithmulti-fingered hand

根据力螺旋理论［3-5］，作用在刚体上的任何力系总可以合成为一个作用于某直线的集中力和绕该直线的力矩（当被抓物体为爆炸物时，可以不考虑），这种力和力矩合称为力螺旋Fext，手指接触力映射到物体的外力螺旋可表达为

其中，G为抓取矩阵，是手指接触力与物体所受力螺旋之间的映射，称为抓取映射.

当有m个手指与物体接触时，其抓取矩阵为

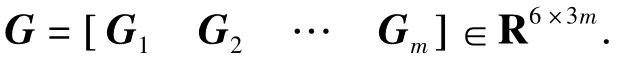
抓取矩阵与手指抓取位置有关.因此，必须对爆炸物的抓取位置进行规划，寻求最有利的抓取模式.

以多指手可以抓取的最大外力螺旋（即爆炸物重量）为优化目标，其优化目标函数为min-Fext，同时考虑各种抓取模数下的约束条件［6-9］，建立优化模型.

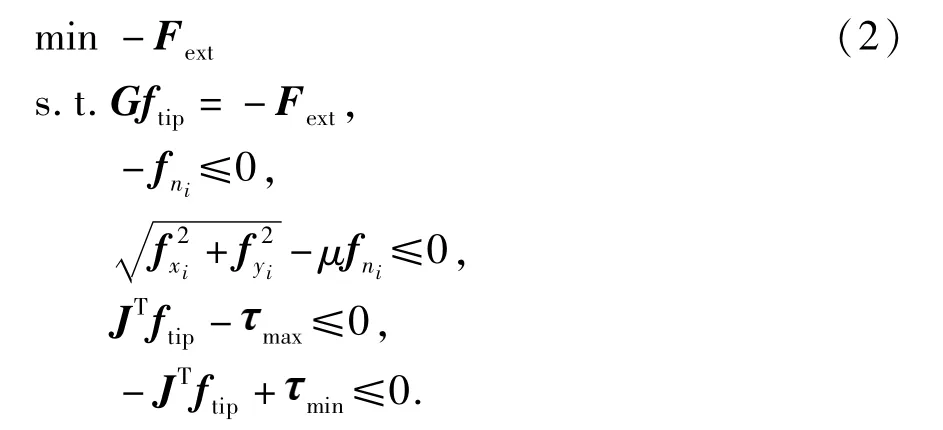
式中，为关节力矩，可以通过雅可比矩阵来描述，建立手指接触力与关节力矩之间的关系［10-12］，

式中，=[12…m]∊R3m×1，J为手指的雅可比矩阵.

2 抓取实例及结果分析

根据人手的抓取经验，在所有可抓取的爆炸物形状中，球形或圆柱形爆炸物是最难以抓取的，也就是抓取稳定性最差.因此，球形爆炸物的抓取研究更有难度和代表性.

假设多指手共有3个手指（m=3），爆炸物为一单位球体.指尖与爆炸物之间的接触为摩擦点接触，手指与爆炸物之间不产生滑动.多指手抓取爆炸物的抓取模型如图2所示.用｛O｝表示物体坐标系Oxyz，以Ok1作为x轴坐标，取δ1为手指k2的接触点在Oxy平面投影与Ox轴的夹角；δ2为Ok2与Oxy平面的夹角；δ3为手指k3的接触点在Oxy平面投影与Ox轴的夹角；δ4为Ok3与Oxy平面的夹角.这样手指k2和k3抓取位置由参数δ1、δ2、δ3、δ4确定.

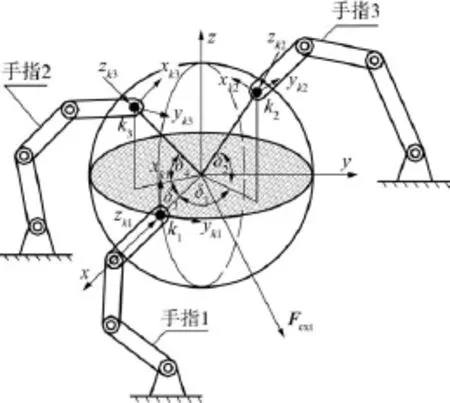
图2 多指手抓取球形爆炸物Fig.2 Spherical explosive grasped bymulti-fingered hand

根据计算可求得接触点k1、k2和k33个手指的抓取矩阵：

最后得到抓取该球体的抓取矩阵：

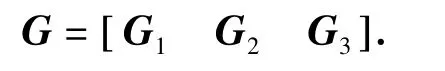
显然，抓取矩阵G是δ的函数，不同的δ值意味着不同的抓取位置，当δ确定时，即手指与爆炸物的接触点确定时，抓取矩阵G也就确定了.

抓取位置变量δ1、δ2、δ3、δ4的取值在理论上有无限种组合.而且约束条件中的摩擦力约束为非线性约束，使得寻优过程复杂化.文中采用BP神经网络求解非线性优化问题.

下面运用BP神经网络分别从不同抓取位置对抓取规划进行分析.

2.1 给定手指1的抓取位置时手指2和3对抓取能力的影响

根据人手的抓取经验，当多指手抓取球体的最大圆截面位置时机器人可抓取爆炸物重量是最大的［13-15］.因此，当手指1抓取大圆上的给定位置时，取δ2=δ4=0，于是抓取矩阵中仅含有抓取变量δ1和δ3.

运用神经网络进行优化［16］，其训练样本来自上述优化模型的解，先将δ1和δ3变量离散化，即在0≤δ1≤240°和120°≤δ3≤360°范围内取值，然后运用优化方法获得对应的δ1和δ3的优化结果，并将其作为网络的训练样本.建立以δ1和δ3为输入，最大外力螺旋Fext为输出的BP神经网络模型，如图3所示.

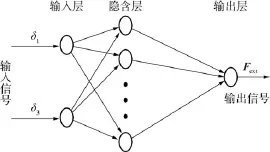
图3 神经网络模型Fig.3 Neural network model

上述模型的输入信号参数为2个，隐含层中的神经元采用S型变换函数，输出层为线性函数.将经过训练后的网络进行拟合仿真，获得多指手抓取位置与最大外力螺旋的对应关系，如图4和图5所示.

从仿真结果可知，δ1=120°、δ3=240°、δ2=δ4=0°处是机器人多指手可以抓取最大重量的爆炸物的位置，如图5中的D点位置，显然，多指手均匀分布在爆炸物的最大圆上，手指间的夹角为120°.

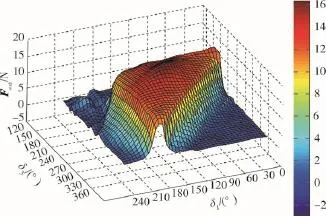
图4 抓取位置与最大外力螺旋的关系Fig.4 Relation between the grasping position and the maximal external wrench

图5 抓取位置与最大外力螺旋的等值线图Fig.5 Contour map of the grasping position and the maximal external wrench

2.2 给定手指1和2的抓取位置时手指3对抓取能力的影响

当手指1和手指2分别固定在大圆平面上，且两手指的相对夹角时，多指手的抓取能力取决于手指3的位置的变化.运用神经网络进行运算仿真，其结果如图6所示.

由图6可以看出，当给定手指1和手指2的抓取位置，手指3最佳抓取位置位于大圆上δ4=0°处，而且只有当δ3=240°时可以抓取的爆炸物重量为最大.这表明，不管抓取位置如何变化，其最佳抓取位置不变，均匀分布在球体的最大圆上.图7为手指3在最大圆截面上的变化角度δ3与爆炸物重量的关系.

2.3 δ1=δ4=90°、δ2=δ3=0°时的抓取能力分析

δ1=δ4=90°、δ2=δ3=0°时，手指与爆炸物的接触位置如图8中的k1、k2和k3点.多指手可以抓取的爆炸物重量为零，抓取不满足力封闭.显然，抓取结果与人手抓取一样无法实现.

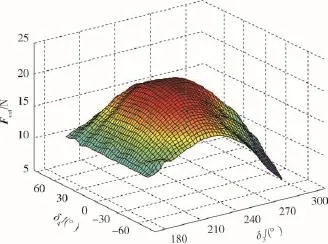
图6 抓取能力与手指3的位置的关系Fig.6 Positional relationship between the grasping ability and the finger 3

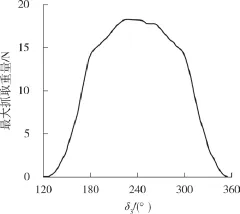
图7 手指3抓取位置与抓取重量的关系Fig.7 Relationship between the position and the grasping weight of finger 3

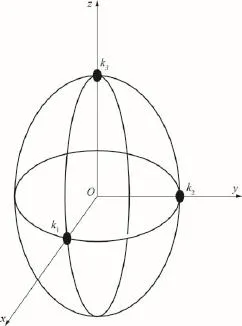
图8 δ1=δ3=δ4=90°，δ2=0°时的抓取位置Fig.8 Grasping position whenδ1=δ3=δ4=90°andδ2=0°

2.4 δ1=δ2=δ3=δ4=0°时的抓取能力分析

当δ1=δ2=δ3=δ4=0°时，手指与爆炸物的接触位置位于同一点即k1，从图4和5可以看出，抓取不满足力封闭，即抓取最大爆炸物重量为零，这与人的抓取经验相一致.

另外，从图4和图5还可以看出，当δ1≠120°、δ3≠240°，也就是当3个手指不位于最大抓取位置时，多指手还是可以抓取一定重量爆炸物.只有当抓取位置位于三角形以外时，多指手才丧失了抓取能力.根据这一结论，可以得出手指抓取圆形爆炸物时能相对稳定的夹持范围如图9所示.表1给出了不同抓取位置的比较.

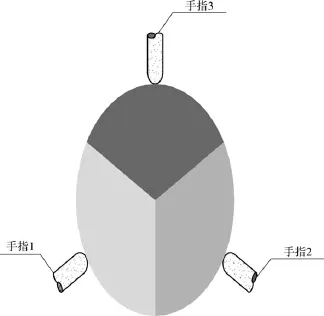
图9 可抓取范围Fig.9 Range for grasping

表1 不同抓取位置的比较Table 1 Comparison of different grasping positions

另外，当被抓爆炸物为非球状时，上述结论仍然适用.因为根据人手抓取经验，当手指接触点距质心最近时其抓取稳定性最好，因此，手指可能的抓取位置如图10所示.

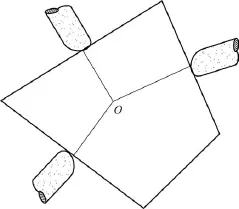
图10 非球形爆炸物的抓取模型Fig.10 Graspingmodel of nonspherical explosive

3 结论

（1）多指手抓取爆炸物的位置与爆炸物的重量存在一定的映射关系，不同的抓取位置对应不同的抓取重量，只有当抓取位置均布在爆炸物的大圆上时，多指手具有最大的抓取能力，此结论对于非圆形爆炸物同样适用.

（2）多指手的抓取位置不是唯一的，只要多指手位于一定的抓取区域，满足力封闭条件，就可以抓取一定重量的爆炸物，跟人手抓取经验一样.因此，当运用多指手进行排爆作业时，并不需要要求多指手一定要按照最大圆的抓取位置抓取.本研究给排爆机器人处理爆炸物提供很大的灵活性和可操作性.

［1］ 王野，王田苗，裴葆青，等.危险作业机器人关键技术综述［J］.机器人技术与应用，2005，10（6）：23-31. Wang ye，Wang Tian-miao，Pei Bao-qing，etal.An overview of the key technology of hazardous operation robot［J］. Robot Technique and Application，2005，10（6）：23-31.

［2］ Yoshikawa T.Manipulability of robotic mechanisms［J］. The International Journal of Robotics Research，1985，4（2）：3-9.

［3］ Richard R M，Li Zexiang.Amathmatical introduction to roboticmanipulation［M］.Boca Raton：CRC Press Inc.，1994.

［4］ 郭语，孙志峻.机器人多指手的多目标优化抓取规划［J］.东南大学学报：自然科学版，2012，42（4）：643-648. Guo Yu，Sun Zhi-jun.Multi-objective optimization grasping planning formultifingered robot hand［J］.Journal of Southeast University：Natural Science Edition，2012，42（4）：643-648.

［5］ Chun-Hsu Ko，Shih-Hsiung Lin.Motion planning ofmultifingered hand-arm system with optimal grasping force［C］∥IEEE 2nd International Symposium on Next-Generation Electronics.NewYork：IEEE Robotics and Automation Society：202-265.

［6］ Bruno Siciliano.A grasping force optimization algorithm formultiarm robots with multifingered hands［J］.IEEE Transactions on Robotics，2013，29（1）：55-67.

［7］ Lippiello，Vincenzo.Visual grasp planning for unknown objects using multifingered robotic hand［J］.IEEE/ ASME Transactions on Mechatronics，2013，18（3）：1050-1059.

［8］ Takayoshi Yamada，Manabu Yamada.Stability analysis of multiple objects grasped bymultifingered handswith revolute joints in 2D［C］∥International Conference on Mechatronics and Automation.NewYork：IEEE Robotics and Automation Society，2012，29（1）：1785-1792.

［9］ Li Qiang，Robert Haschke.Rotarysurface objectmanipulation by multifingered robot hand［C］∥The 7th German Conference on Robotics.Berlin：German Association of Robotics，2012：1-6.

［10］ Zhang Zichen，Gu J.Grasp planning of 3D objects using genetic algorithm［C］∥IEEE International Conference on Automation and Logistics.NewYork：IEEE Robotics and Automation Society，2012：646-651.

［11］ Ko Chun-Hsu，Chen Jein-Shan.Optimal graspingmanipulation formultifingered robots using semismooth newton method［J］.Mathematical Problems in Engineering，2013，35（10）：1-10.

［12］ Zheng Yu，Manocha.On computing reliable optimal grasping forces［J］.IEEE Transactions on Robotics，2012，28（3）：619-633.

［13］ Liu Guan-feng，Li Ze-xiang.Real-time grasping-force optimization for multifingered manipulation theory and experiments［J］.IEEE Transactions on Mechatronics，2004，9（1）：65-76.

［14］ Akio Namiki，Masatoshi Ishikawa.The analysis of highspeed catching with a multifingered robot hand［C］∥IEEE International Conference on Robotics and Automation.NewYork：IEEE Robotics and Automation Society，2005，2666-2671.

［15］ Haidacher S，Hirzinger G.Contact point identification in multi-fingered grasps exploiting kinematic constraints［C］∥International Conference on Robotics and Automation.New York：IEEE，2002：1597-1603.

［16］ 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京：清华大学出版社，2005.

Investigation into the Ability of M ulti-Fingered Dexterous Hand to Grasp an Exp losive

Mo Hai-jun Lin Zhi-sheng
（School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510640，Guangdong，China）

On the basis of the force screw theory，the relationship between the graspmatrix ofmulti-fingered dexterous hand and the external force screw is established to investigate the ability ofmulti-fingered dexterous hand to grasp an explosive.Firstly，amechanicalmodel ofmulti-fingered dexterous hand which can grasp an explosive is constructed and the parameters influencing the grasp are determined.Then，with the maximum grasp being the goal，amathematicalmodel of the grasp is constructed under the constraint of force closure.Finally，through the neural network and optimization methods，themulti-fingered dexterous hand grasping an explosive is simulated，so as to reveal corresponding the relationship between the grasp position and the explosive weight.Thus，the best grasp position is obtained.

multi-fingered dexterous hand；grasp ability；neural networks；explosive

TG242

10.3969/j.issn.1000-565X.2015.07.017

1000-565X（2015）07-0124-06

2014-12-08

国家自然科学基金资助项目（51175182）

Foundation item：Supported by the National Natural Science Foundation of China（51175182）

莫海军（1966-），男，博士，副教授，主要从事机器人多指手抓取及排爆机器人研究.E-mail：mohj@scut.edu.cn