钢筋-纤维自密实混凝土梁受弯性能与承载力分析*

宁喜亮 丁一宁

（大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024）

钢筋-纤维自密实混凝土梁受弯性能与承载力分析*

宁喜亮 丁一宁†

（大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024）

通过四点弯曲试验得到钢筋-纤维自密实混凝土梁式构件的荷载-跨中挠度曲线、荷载-纵筋应变曲线和破坏形态，对梁式构件的受弯承载力及纤维与钢筋的混杂效应进行了分析.结果表明：钢纤维的加入使钢筋-纤维自密实混凝土梁式构件的抗弯承载力提高了10%～42%.考虑钢纤维跨越裂缝的传力机理及分布情况提出了钢筋-纤维混凝土梁式构件受弯承载力计算公式，并与ACI 544和CECS 38：2004的公式进行了对比，计算结果表明：文中建议公式计算的受弯承载力与试验结果最为接近，可用于钢筋-纤维自密实混凝土梁式构件的受弯分析与设计.

钢筋；钢纤维；自密实混凝土；钢筋-纤维自密实混凝土梁；受弯承载力

混凝土是一种抗拉强度远低于其抗压强度的脆性材料，很容易受拉开裂，在普通混凝土中加入纤维能够有效改善混凝土的抗拉性能、抗冲击性能以及耗能能力，具有良好的限裂效应［1-5］.然而纤维的作用能否充分发挥取决于纤维与混凝土基体之间的粘结性能及纤维在混凝土基体中的分布情况.纤维的掺入会降低新拌混凝土的工作性能，纤维在混凝土基体中也难以分布均匀，使纤维与混凝土基体以及钢筋与混凝土基体之间的粘结性能受到影响，进而影响到结构的安全性和耐久性［6-8］.

自密实混凝土（SCC）作为一种新型高性能混凝土，无需振捣便可在自重作用下将模板填充密实，具有良好的间隙通过能力和抵抗离析能力，使得基体中的骨料与浆体界面的粘结性能优于普通混凝土，内部缺陷少，因而在国内外已经大量应用于工程结构［9-11］.研究表明［12-14］，在SCC中加入适量钢纤维配制的钢纤维自密实混凝土（SFRSCC）融合了自密实混凝土和纤维混凝土的优点，不但具有良好的工作性和抗离析性能，而且可以明显改善钢筋与混凝土的粘结握裹性能和抗裂性能，具有较高的研究价值.

截止目前，国内外学者已对钢纤维自密实混凝土进行了一些研究［15-17］，配制同时满足较高工作性、较高强度和韧性的纤维自密实混凝土已不困难.然而，钢纤维自密实混凝土的工程应用还很有限，CCTV新台址工程［18］在型钢混凝土柱中采用了C60的钢纤维自密实混凝土，但只用于控制型钢混凝土柱中可能产生的裂缝，并没有考虑钢纤维对结构或构件承载力的提高作用.缺乏普遍认可的结构设计规范是限制SFRSCC大量工程应用的主要因素，尽管国内外制定了一些钢纤维混凝土的设计规程［19-20］，但大多为半经验公式.

文中研究了配筋率和纤维掺量对钢筋-纤维自密实混凝土梁式构件受弯承载力、变形能力、纵筋应变以及裂缝形态的影响.分析了纤维跨越裂缝的传力机理和纤维在破坏截面的分布情况，提出了考虑纤维作用的钢筋-纤维混凝土梁式构件受弯承载力计算公式，并将计算值与试验值进行了比较.

1 试验

1.1 原材料

混凝土设计强度等级为C60.试验用水泥为P.O 52.5R普通硅酸盐水泥；细骨料为优质河砂，粒径0～5mm，细度模数为2.6，属于中砂；粗骨料为碎石，最大粒径10mm；一级袋装粉煤灰；聚羧酸系高效减水剂.自密实混凝土基准配合比见表1.文中采用DramixRC-80/60-BN端部弯钩型钢纤维（如图1所示），纤维长度为60mm，长径比为80，抗拉强度为1100MPa，纤维根数为4600根/kg，纤维掺量分别为0、30和50 kg/m3.新拌纤维自密实混凝土工作性能与立方体抗压强度的试验结果如表2所示.从表2可看出，掺入钢纤维对混凝土抗压强度没有明显影响，新拌纤维自密实混凝土的各项工作性指标（流动扩展度，J环，L槽）均满足EFNARC［21］的要求.

表1 自密实混凝土配合比Table 1 Mix proportion of self-compacting concrete kg/m3

图1 结构型钢纤维Fig.1 Structural steel fibers

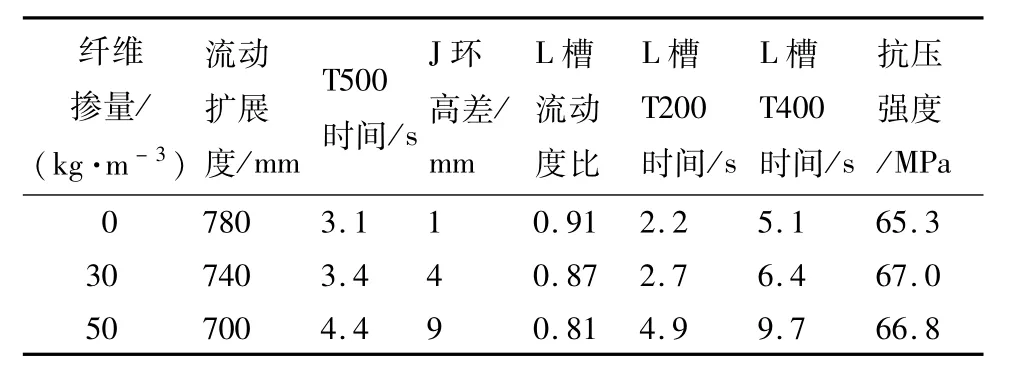
表2 钢纤维自密实混凝土抗压强度与工作性能Table 2 Compressive strength and workability of SFRSCC

1.2 试件设计

设计并制作9根（分为O、A、B 3个系列）钢筋-纤维自密实混凝土梁式构件，构件的几何尺寸和配筋情况如图2所示，截面尺寸均为200mm×300mm，长度l=2 400mm，净跨ln=2 100mm，受拉钢筋采用HRB400级钢筋，配筋率ρs分别为0.44%（310）、0.76%（216）和0.96%（218），钢筋的物理力学性能如表3所示.试件详细设计参数见表4，编号为BS-A-SF30的梁，其中字母A表示梁的配筋率为0.76%，SF30表示钢纤维掺量为30 kg/m3，其余试件编号以此类推.

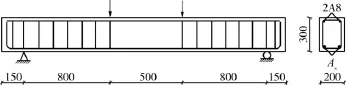
图2 梁式构件的几何尺寸与配筋（单位：mm）Fig.2 Geometry dimension and reinforcement of the beams（Unit：mm）

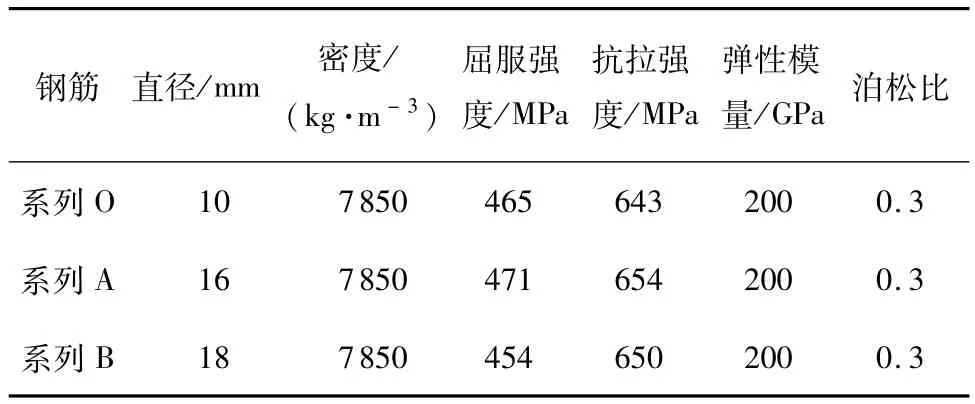
表3 钢筋的力学性能Table 3 Mechanical properties of steel rebars

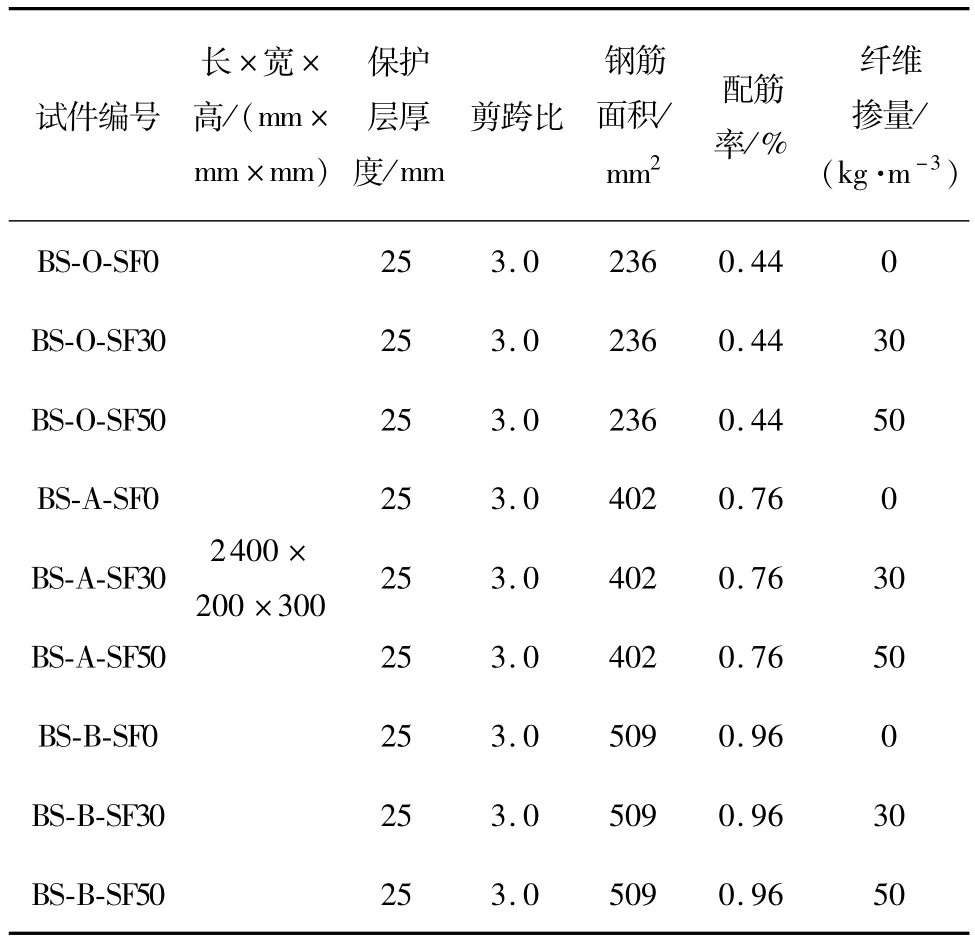
表4 试验梁参数设计Table 4 Design parameters of beams

1.3 试验装置与测试

梁式构件的弯曲试验采用1000 t液压伺服试验机并采取四点加载方式，位移闭环控制，纵筋屈服前加载速率为0.3mm/min，纵筋屈服后加载速率变为0.6mm/min，直至试件破坏.荷载等级为20 kN，每级荷载持续时间约为15min.采用3个位移传感器分别测量试验梁的跨中和加载点处的挠度，并在梁式构件的跨中和加载点处布置电阻应变片测量纵筋应变，梁式构件加载与数据测点布置如图3所示.

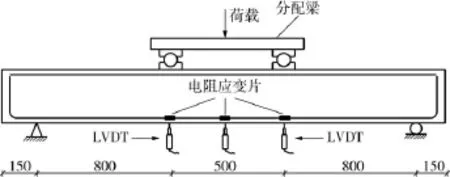
图3 梁式构件加载与数据测量装置（单位：mm）Fig.3 Loading and measuring arrangement of beams（Unit：mm）

2 试验结果与分析

2.1 破坏形态

钢筋-纤维自密实混凝土梁BS-A-SF0和BSA-SF50的破坏形态如图4所示.

图4 梁式构件破坏形态Fig.4 Failure pattern of beams

由图4可以看出，由于梁BS-A-SF0的配筋率较低（ρs=0.76%），直到加载结束，混凝土尚未被压碎；而掺50kg/m3钢纤维后，由于纤维与钢筋共同承担拉力，增加了梁的抗弯承载力，使得梁BS-A-SF50受压区混凝土被压碎，弯曲破坏特征明显.掺50 kg/m3钢纤维后，梁式构件BS-A-SF50的裂缝条数增加，裂缝宽度和裂缝间距明显减小.由图4（a）还可以看出，不掺纤维的钢筋自密实混凝土梁（BS-A-SF0），破坏时裂缝宽度在纯弯段不同位置扩展，呈现出较宽的裂缝与较大的挠度；而钢纤维掺量为50 kg/m3的钢筋自密实混凝土梁（BS-A-SF50），破坏时裂缝主要在跨中一条主裂缝处扩展（见图4（b）），使得试验梁在相同荷载下，产生较小的挠度，该现象又称为“变形局部化现象”［22-23］，主要出现在配筋率较低的钢筋-纤维混凝土受弯构件中.

2.2 荷载-跨中挠度曲线

O、A、B 3个系列梁式构件的开裂荷载、极限荷载及相应的挠度见表5，荷载-跨中挠度曲线如图5所示.

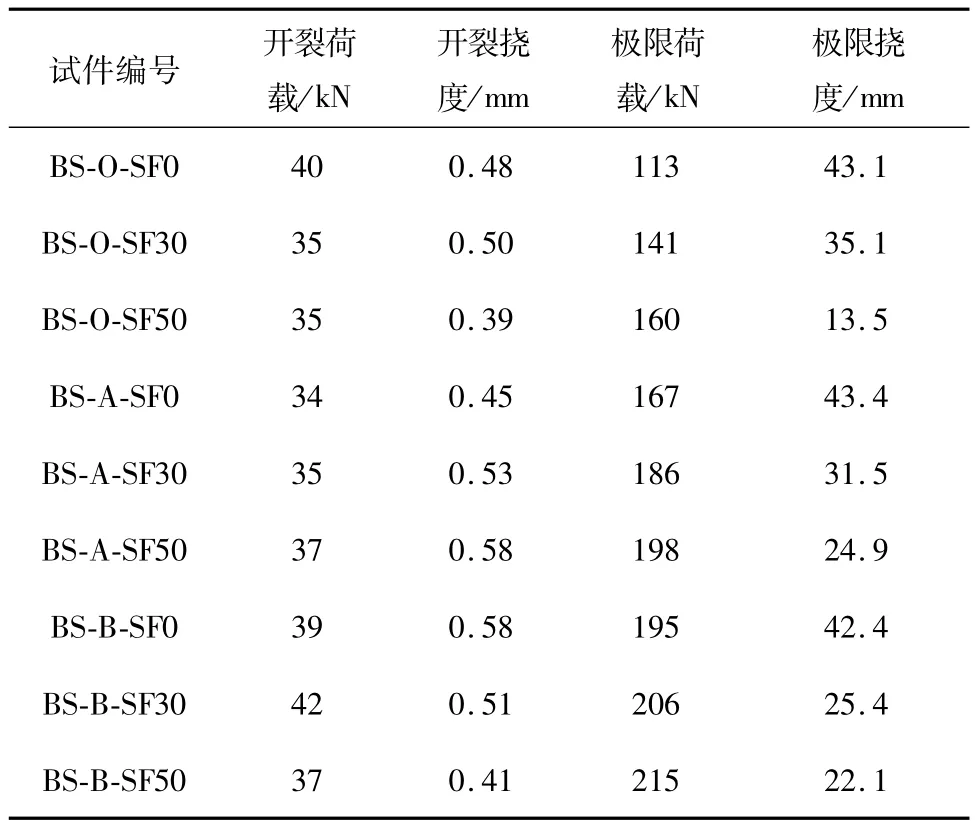
表5 试验梁开裂荷载、极限荷载及对应挠度1）Table 5 Cracking load，ultimate load and corresponding deflection of beams

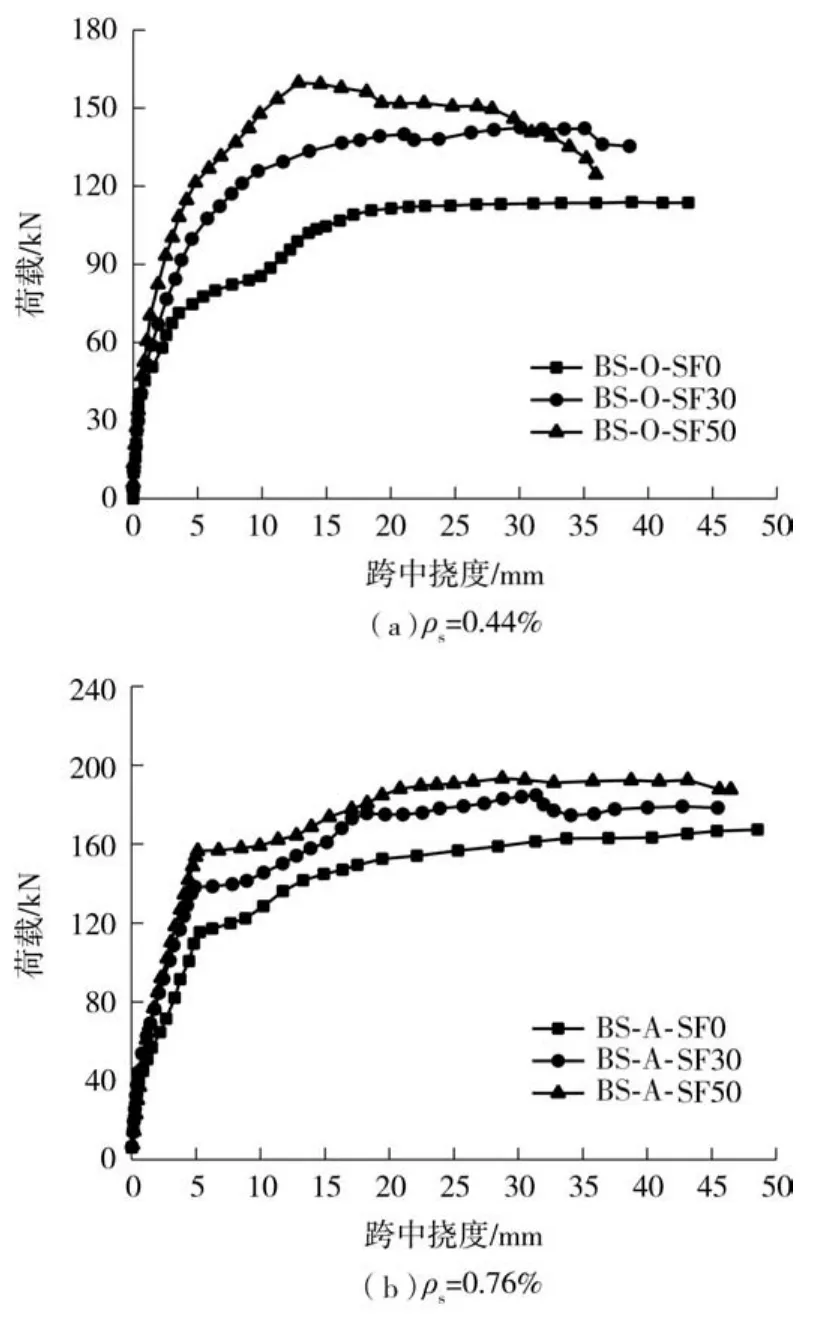
图5 不同配筋率下试验梁荷载-跨中挠度曲线Fig.5 Load-midspan deflection curves of beams with different reinforcement ratios

由表5和图5可以看出，钢纤维的掺入对钢筋自密实混凝土梁的开裂荷载影响不大；混凝土开裂后，试验梁的荷载-跨中挠度曲线斜率减小，表现为刚度降低.此时三维随机分布的钢纤维在混凝土开裂后能够跨越裂纹面，通过与混凝土基体的粘结作用传递应力，提高了构件开裂截面的刚度，使荷载-跨中挠度曲线的斜率明显高于普通钢筋自密实混凝土梁式构件.

2.2.1 纤维掺量的影响

试验梁的极限荷载与纤维掺量的关系如图6所示.

由图6和表5可看出：配筋率为0.44%时，与不掺纤维的钢筋自密实混凝土梁BS-O-SF0相比，梁BS-A-SF30和BS-A-SF50的极限荷载分别提高了25%和42%；配筋率为0.76%时，与不掺纤维的梁BS-A-SF0相比，梁BS-A-SF30和BS-A-SF50的极限荷载分别提高了11%和19%；配筋率为0.96%时，与不掺纤维的梁BS-B-SF0相比，梁BS-B-SF30和BS-B-SF50的极限荷载分别提高了6%和10%.

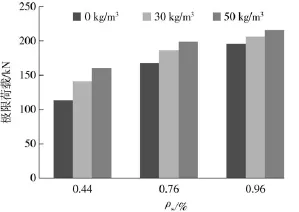
图6 极限荷载随钢纤维掺量的变化Fig.6 Changes of ultimate load with steel fiber content

由上述分析可知，纤维的掺入可明显提高钢筋自密实混凝土梁式构件的抗弯承载力，尤其在配筋率较低的情况（ρs=0.44%）下，纤维的增强作用更明显，钢纤维掺量为50 kg/m3时，可使试验梁的极限荷载提高42%；但随着配筋率的提高，纤维对抗弯承载力的提高却随之减弱，在配筋率为0.96%的条件下，钢纤维掺量为50 kg/m3时，抗弯承载力只提高了10%.因为相同掺量的钢纤维对试验梁抗弯承载力的贡献是相同的，而配筋率较高的普通自密实混凝土梁式构件抗弯承载力较高，纤维的作用变得不够明显，故随着配筋率的提高，钢纤维对梁式构件抗弯承载力的提高作用减弱.

2.2.2 配筋率的影响

不同配筋率的试验梁的荷载-跨中挠度曲线如图7所示.

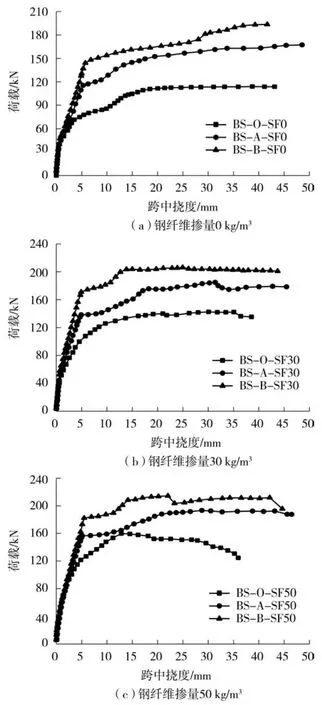
图7 不同钢纤维掺量下试验梁荷载-跨中挠度曲线Fig.7 Load-midspan deflection of beamswith differentsteel fiber contents

由图7和表5可看出：对比不掺加钢纤维的钢筋自密实混凝土梁式构件，与梁BS-O-SF0相比，梁BS-A-SF0和BS-B-SF0的极限荷载分别提高了48%和73%；对比钢纤维掺量为30kg/m3的试验梁，与梁BS-O-SF30相比，梁BS-A-SF30和BS-B-SF30的极限荷载分别增加了32%和46%；对比钢纤维掺量为50 kg/m3的试验梁，与梁BS-O-SF50相比，梁BS-ASF50和BS-B-SF50的极限荷载分别提高了24%和34%.

由以上分析可知，在不掺钢纤维时，配筋率对试验梁的抗弯极限荷载影响很大，配筋率由0.44%增大到0.96%时，极限荷载的提高达73%；而在钢筋自密实混凝土梁式构件中加入钢纤维后，随着配筋率的提高，试验梁极限荷载之间的差距不断缩小，当钢纤维掺量为50 kg/m3时，配筋率由0.44%增大到0.96%，极限荷载提高了34%，比不掺钢纤维的情况降低了约一半.

2.2.3 钢筋与钢纤维的正混杂效应

由表5可看出：钢纤维掺量为50 kg/m3的低配筋率试验梁BS-O-SF50与配筋率较高的试验梁BSA-SF0相比，极限荷载略有降低；而钢纤维掺量为50 kg/m3的较低配筋率试验梁BS-A-SF50与较高配筋率的试验梁BS-B-SF0相比，极限荷载提高了2.5%.由于钢筋与钢纤维在混凝土开裂后共同承担拉力，表现出较好的正混杂效应.由上述分析可知，钢纤维掺量为50 kg/m3时，可在不降低试验梁抗弯承载力的情况下使配筋率降低0.2%，替代梁式构件的最小配筋率［24］.

2.3 荷载-纵筋应变曲线

图8 A系列梁荷载-纵筋应变曲线Fig.8 Load-steel strain curves of series A beams

A系列试验梁荷载-纵筋应变曲线如图8所示.由图8可以看出：在混凝土开裂前，3条曲线几乎重合，近似为直线，因为钢筋、钢纤维和混凝土都处于弹性阶段，变形协调，钢纤维的掺入对钢筋应变影响不大；而在混凝土开裂后，开裂截面处钢筋发生应力重分布，钢筋应变迅速增大，由于纤维跨越裂纹面传递部分拉力，限制了钢筋应变的继续增大，使得在相同应变下，掺加钢纤维的试验梁的抗弯能力得到明显提高.在纵筋应变为2×10-3时，与不掺钢纤维的试验梁BS-A-SF0相比，钢纤维掺量为30和50 kg/m3的试验梁的抗弯荷载分别提高了15%和22%.

3 正截面受弯承载力分析

3.1 受弯承载力计算公式

普通混凝土的抗拉强度远小于其抗压强度，因此传统的钢筋混凝土理论在计算梁式构件受弯承载力时，不考虑混凝土受拉的贡献［25］.然而，由试验结果可知，钢纤维的掺入对钢筋自密实混凝土梁式构件的抗弯承载力有明显提高作用，尤其是在配筋率较低的情况（ρs=0.44%）下，钢纤维掺量为50 kg/m3时，钢筋自密实混凝土梁的抗弯承载力提高42%；因此，非常有必要在钢筋-纤维混凝土梁式构件受弯承载力计算中引入纤维的作用，得到更接近钢筋-纤维混凝土梁式构件真实抗弯承载力的预测值.

ACI 544［19］较早地在计算钢筋-纤维混凝土梁式构件受弯承载力时考虑纤维对开裂后受拉区混凝土的贡献.图9为ACI 544采用的截面应力和应变分布图，根据传统钢筋混凝土理论的平截面假定和平衡方程，并考虑纤维对开裂后受拉区混凝土的作用，抗弯承载力公式表示为

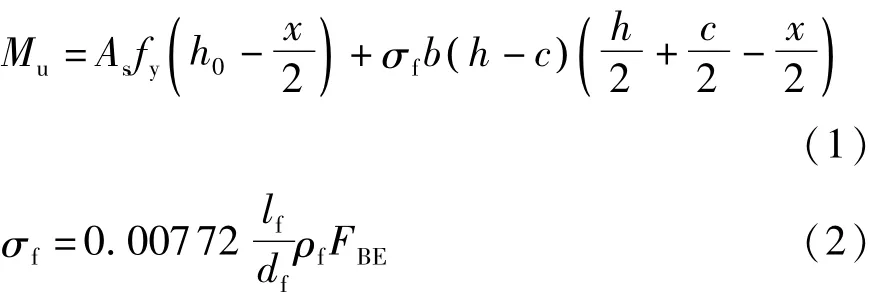
式中：c为中和轴高度；x为受压区等效矩形应力图高度；h0为截面有效高度；σf为纤维混凝土开裂后等效矩形应力图抗拉强度；lf/df为纤维长径比；ρf为纤维体积百分数；FBE为考虑纤维特性粘结有效系数，对于端部弯钩型钢纤维，取1.2；0.007 72为经验系数.

ACI 544计算纤维对开裂后受拉区混凝土作用的公式是半经验性的，没能很好地解释纤维作用的机理.文中在ACI 544计算公式基础上对受拉区纤维的作用做进一步分析，考虑纤维在开裂截面的分布及纤维跨越裂缝的传力机理，采用文献［26］中纤维对开裂后混凝土抗拉能力增强公式：

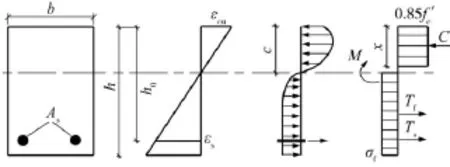
图9 钢筋-钢纤维混凝土梁截面应力与应变分布Fig.9 Stress and strain distribution of SFRC beam containing conventional steel rebars

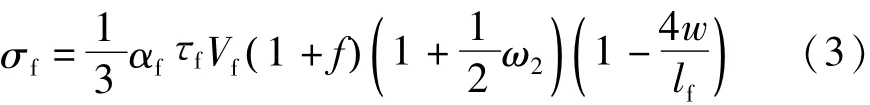
式中：αf为纤维的长径比（αf=lf/df，lf为纤维长度；df为纤维直径）；Vf为纤维体积掺量；f为纤维与混凝土基体界面粘结强度，对于端部弯钩型纤维，取2.5fct［27］；fct为混凝土基体的抗拉强度，MPa；f为纤维与混凝土裂缝边缘剪切摩擦系数，取1/3［26］；ω2为纤维的二维分布方向系数；w为裂缝宽度.

为方便在设计中应用，考虑纤维在混凝土基体中三维随机分布，σf表达式可简化为

将式（4）代入到式（1）中，得到修正的抗弯承载力计算公式：

3.2 受弯承载力计算值与试验值的比较

为了验证文中提出的钢筋-纤维混凝土梁式构件受弯承载力计算公式的合理性，将文中提出的抗弯承载力计算公式（式（5））、ACI 544［19］以及CECS 38：2004［20］中的计算公式的计算值与文中的试验值进行对比，结果如表6所示.

CECS 38：2004［20］中正截面受弯承载力计算公式为

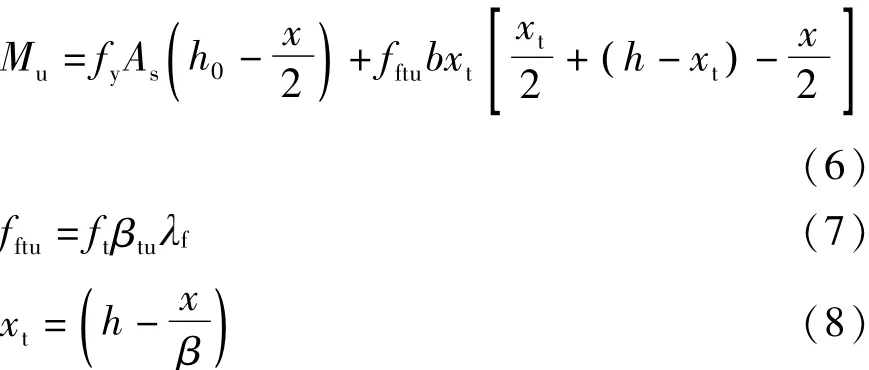
式中：fftu为受拉区钢纤维混凝土等效矩形应力图形的抗拉强度；βtu为钢纤维对构件截面受拉区抗拉作用的影响系数，对于受弯构件，取1.3；f为钢纤维掺量特征值，f=Vflf/df；xt为受拉区等效矩形应力图高度；β为混凝土抗压强度等级影响系数，按现行国家标准《混凝土结构设计规范》（GB 50010—2010）［24］采用.

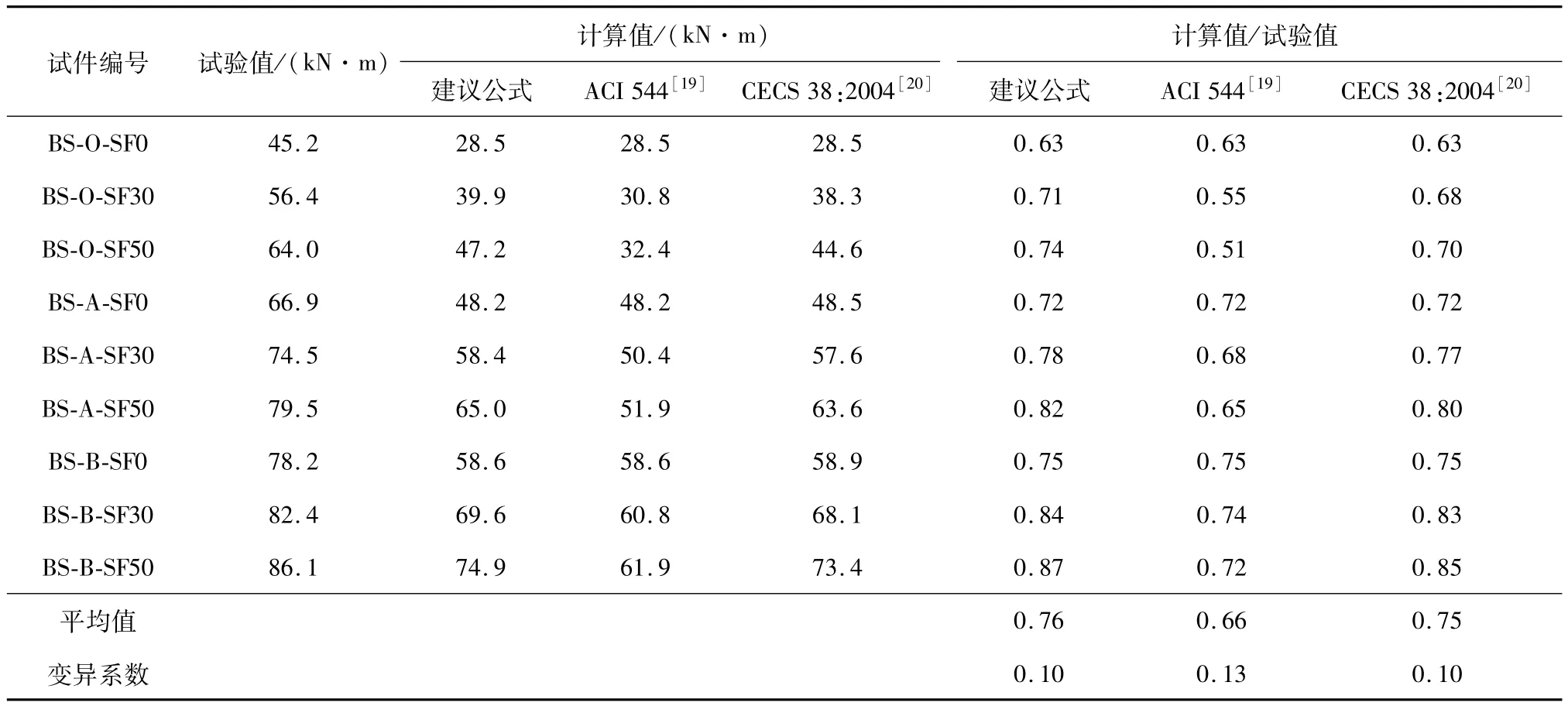
表6 钢筋-纤维混凝土梁受弯承载力Table 6 Flexural capacity of steel rebars reinforced SFRC beam

由表6的对比结果可知，3个公式计算结果均较为保守，其中按照文中建议公式的计算结果与试验值最为接近，且变异系数较小，说明文中建议的计算公式比较合理，可较为准确地反映钢筋-纤维混凝土梁式构件的受弯机理.

4 结论

通过对9根钢筋-纤维自密实混凝土梁式构件的试验研究，得到如下主要结论：

（1）钢纤维的掺入可明显提高钢筋-自密实混凝土梁式构件的抗弯承载力，改善裂缝形态.

（2）在配筋率较低（ρs=0.44%）的情况下，钢纤维掺量为50 kg/m3时可使极限荷载提高42%；而在配筋率较高（ρs=0.96%）的情况下，钢纤维掺量为50 kg/m3时仅能使极限荷载提高10%.说明纤维掺量相同时，在配筋率较低的试验梁中，钢纤维的作用更加明显.

（3）钢纤维在试验梁开裂后，与钢筋共同承担拉力，表现出明显的正混杂效应，钢纤维掺量为50 kg/m3时，可在不降低试验梁极限荷载的情况下，替代梁式构件的最小配筋率.

（4）钢纤维的掺入可显著地降低裂缝处的钢筋应变，提高开裂截面的刚度，使试验梁在相同荷载下的挠度明显降低.

（5）文中提出的考虑纤维在开裂截面分布与传力机理的钢筋-纤维混凝土梁式构件受弯承载力计算公式能较好地预测钢筋-纤维混凝土梁式构件的受弯承载力，且具有较小的变异系数.

［1］ ACICommittee 544.State-of-the-art report on fiber reinforced concrete（ACI 544.1R-96）［R］.Farmington Hills：American Concrete Institute，1997.

［2］ Brandt A M.Fibre reinforced cement-based（FRC）composites after over 40 years of development in building and civil engineering［J］.Composite Structures，2008，86（1）：3-9.

［3］ Olivito R S，Zuccarello F A.An experimental study on the tensile strength of steel fiber reinforced concrete［J］. Composites Part B：Engineering，2010，41（3）：246-255.

［4］ Soutsos M N，Le T T，Lampropoulos A P.Flexural performance of fibre reinforced concretemade with steel and synthetic fibres［J］.Construction and Building Materials，2012，36：704-710.

［5］ Chen Xiangyu，Ding Yining，Azevedo C.Combined effect of steel fibres and steel rebars on impact resistance of high performance concrete［J］.Journal of Central South University of Technology，2011，18（5）：1677-1684.

［6］ Ferrara L，Park Y D，Shah S P.Correlation among fresh state behavior，fiber dispersion，and toughness properties of SFRCs［J］.Journal of Materials in Civil Engineering，2008，20（7）：493-501.

［7］ Desnerck P，De Schutter G，Taerwe L.Bond behaviour of reinforcing bars in self-compacting concrete：experimental determination by using beam tests［J］.Materials and Structures，2010，43（1）：53-62.

［8］ Cunha V M C F，Barros JA O，Sena-Cruz JM.Pullout behavior of steel fibers in self-compacting concrete［J］.Journal of Materials in Civil Engineering，2009，22（1）：1-9.

［9］ Sonebi M，Tamimi A K，Bartos P J.Performance and cracking behavior of reinforced beams cast with self-consolidating concrete［J］.ACIMaterials Journal，2003，100（6）：492-500.

［10］ Domone P L.Self-compacting concrete：an analysis of 11 years of case studies［J］.Cementand Concrete Composites，2006，28（12）：197-208.

［11］ Cattaneo S，Giussani F，Mola F.Flexural behaviour of reinforced，prestressed and composite self-consolidating concrete beams［J］.Construction and Building Materials，2012，36：826-837.

［12］ Sahmaran M，Yurtseven A，Ozgur Yaman I.Workability of hybrid fiber reinforced self-compacting concrete［J］. Building and Environment，2005，40（12）：1672-1677.

［13］ Ding Yining，Liu Siguo，Zhang Yulin，et al.The investigation on the workability of fibre cocktail reinforced selfcompacting high performance concrete［J］.Construction and Building Materials，2008，22（7）：1462-1470.

［14］ Pereira E N，Barros J A O，Cames A.Steel fiber-reinforced self-compacting concrete：experimental research and numerical simulation［J］.Journal of Structural Engineering，2008，134（8）：1310-1321.

［15］ Ding Yining，You Zhiguo，Jalali S.The composite effect of steel fibres and stirrups on the shear behaviour of beams using self-consolidating concrete［J］.Engineering Structures，2011，33（1）：107-117.

［16］ Pajᶏk M，Ponikiewski T.Flexural behavior of self-compacting concrete reinforced with different types of steel fibers［J］.Construction and Building Materials，2013，47：397-408.

［17］ Aslani F，Nejadi S.Self-compacting concrete incorporating steel and polypropylene fibers：compressive and tensile strengths，moduli of elasticity and rupture，compressive stress-strain curve，and energy dissipated under compression［J］.Composites Part B：Engineering，2013，53：121-133.

［18］ 余成行，刘敬宇，肖鑫.C60钢纤维自密实混凝土的配合比设计和应用［J］.混凝土，2007，29（7）：74-78.Yu Cheng-hang，Liu Jing-yu，Xiao Xin.Mixture ratio design and application of C60 self-compacting concrete reinforced by steel fiber［J］.Concrete，2007，29（7）：74-78.

［19］ ACICommittee 544，Design considerations for steel fiber reinforced concrete［S］.

［20］ CECS 38：2004，纤维混凝土结构技术规程［S］.

［21］ EFNARC，Specification，guidelines for self-compacting concrete［S］.

［22］ Dancygier A N，Savir Z.Flexural behavior of HSFRC with low reinforcement ratios［J］.Engineering Structures，2006，28（11）：1503-1512.

［23］ Schumacher P.Rotation capacity of self-compacting steel fiber reinforced concrete［D］.Delft：Delft University of Technology，2006.

［24］ GB 50010—2010，混凝土结构设计规范［S］.

［25］ 叶列平.混凝土结构［M］.2版.北京：清华大学出版社，2006.

［26］ Stroeven P.Stereological principles of spatial modeling applied to steel fiber-reinforced concrete in tension［J］. ACIMaterial Journal，2009，106（3）：213-222.

［27］ Voo JY L，Foster，SJ.Variable engagementmodel for fibre reinforced concretein tension［R］.Sydney：The University of New South Wales，2003.

Analysis of Flexural Behavior and Bearing Capacity of Steel Rebar-Reinforced Steel Fiber-Reinforced Self-Com pacting Concrete Beam s

Ning Xi-liang Ding Yi-ning
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，Liaoning，China）

Bending tests under four point loading were conducted on steel rebar-reinforced steel fiber-reinforced self-compacting concrete（SFRSCC）beams，and the corresponding loading-mid-span deflection curve，longitudinal reinforcement strain-longitudinal reinforcement strain curve and failure mode were obtained.The flexural bearing capacity of the beams and the hybrid effectof steel rebar andmacro steel fiberswere also examined.It is found that the addition of steel fibers can improve the flexural bearing capacity by 10%～42%.Moreover，by taking into account the steel fiber distribution and its force transfermechanism crossing the crack，a calculation formula is proposed to predict the flexural bearing capacity of the beams，and it is compared with the formulas of ACI 544 and CECS 38：2004.Calculation results show that the proposed formula has a better fitwith the test results.Thus，it is suitable for the flexural analysis and design of SFRSCC beams.

steel rebar；steel fibers；self-compacting concrete；rebar-reinforced steel fiber-reinforced self-compacting concrete beam；flexural bearing capacity

TU528.572；TU375.1

10.3969/j.issn.1000-565X.2015.07.007

1000-565X（2015）07-0042-08

2014-10-13

国家自然科学基金面上项目（51578019）

Foundation item：Supported by the General Program of National Natural Science Foundation of China（51578019）

宁喜亮（1984-），男，博士生，主要从事纤维高性能混凝土试验与理论研究.E-mail：ning-tony@163.com

†通信作者：丁一宁（1962-），男，教授，博士生导师，主要从事纤维高性能混凝土理论与工程应用研究.E-mail：ynding@hotmail. com