环境星归一化植被指数时间序列滤波算法比较

刘寒，冯莉，朱榴骏，黄银友

(1.南京大学江苏省地理信息技术重点实验室，南京 210023；2.南京大学卫星测绘技术与应用国家测绘地理信息局重点实验室，南京 210023；3.南京大学地理信息科学系，南京 210023)

环境星归一化植被指数时间序列滤波算法比较

刘寒1，2，3，冯莉1，2，3，朱榴骏1，2，3，黄银友1，2，3

(1.南京大学江苏省地理信息技术重点实验室，南京 210023；2.南京大学卫星测绘技术与应用国家测绘地理信息局重点实验室，南京 210023；3.南京大学地理信息科学系，南京 210023)

由于环境卫星成像条件和卫星平台的限制，针对环境卫星归一化植被指数(HJ NDVI)时间序列中存在较多噪音的现象，该文比较分析了Savitzky-Golay(S-G)滤波法、非对称高斯函数拟合法(AG)、双逻辑曲线拟合法(DL)和时间序列谐波分析法(Hants)4种滤波算法。建立了南京市典型植被类型区域的HJ NDVI时间序列，对4种滤波方法进行实验。对比纯像元样点、样区的滤波结果以及滤波后5类典型植被的分类精度，评价4种滤波方法的滤波效果，并利用MODIS NDVI时序数据验证结果可靠性。结果表明：滑动窗口大小为5的S-G滤波的滤波效果最佳。该研究结论为基于HJ NDVI时间序列的应用研究滤波方法选择提供参考。

城市植被；时空分辨率；HJ NDVI时间序列；滤波；南京市

0 引 言

卫星传感器所获取的NDVI时间序列数据能够精确地反映陆地生态系统植被的生长状态和季相、年际变化特征，已广泛应用与全球与区域生态环境变化监测与模拟、植被覆盖动态变化研究、植被物候特征识别与信息提取等许多方面[1-3]。目前常用的NDVI时间序列主要来自NOAA AVHRR、SPOT VEGETATION和TERRA/AQUA MODIS等传感器[4]。但受其空间分辨率较低的影响，NDVI时间序列产品难以满足中小尺度研究和应用。

近三十年，关于建立高质量NDVI时间序列滤波方法的研究层出不穷。Viovy等[5]在1992年提出了基于最佳斜率指数提取的滤波方法(BISE)，试图通过滑动合成时段来消除NDVI时间序列中的噪音；1996年荷兰地理信息中心的研究人员Verhoef等[6]开发出了NDVI时间序列调和分析拟合法，改进了传统的只能处理等时间间隔和信噪比较高数据的基于快速傅里叶算法的滤波算法；Jönsson和Eklundh[7]在2002年提出了非对称高斯函数拟合算法(Asymmetric Gaussian，AG)，指出其拟合效果优于BISE和基于傅里叶变换的滤波算法；2004年Chen Jin等[8]利用改进的S-G算法对NDVI时间序列数据进行实验，指出其滤波效果优于Sellers等[9]在1994年提出的快速傅里叶变换算法；Beck等[10]提出了一种新的双重逻辑函数拟合算法(DL)，并指出这种算法与AG拟合算法一样比基于快速傅里叶变换的算法具有更高的优越性；2009年Jennifer等[11]对6种滤波算法进行了实验，并进行了定量的对比分析，系统地讨论了各种方法的优劣，指出AG和DL算法优于其他4种算法。现阶段关于滤波方法效果的研究多集中于基于MODIS等常见的NDVI时间序列，并且大多数的研究都局限于对比3种以下的滤波方法，多是对比集成于TIMESAT软件下的3种滤波方法，或是集中讨论一种滤波方法的滤波效果。

2008年我国发射了环境与灾害监测预报小卫星A、B星(HJ-1A/B星，简称HJ卫星)，从发射至今，HJ卫星遥感影像已经构成了时间跨度近6年的时间序列数据，初步具备了构成较长时间的遥感时间序列的能力。HJ卫星以其高时空分辨率的特点在NDVI时间序列的构建上有着很理想的前景。由于HJ卫星成像条件和卫星平台的限制，HJ NDVI时间序列中存在较多噪音，多受薄云影响而导致NDVI值出现下降，为HJ NDVI时间序列数据的应用研究带来一定误差，因此研究HJ NDVI时间序列的最优滤波方法十分必要。 本研究以南京市及周围市郊为研究区，选用S-G滤波、AG拟合法、DL拟合法和Hants 4种方法进行HJ NDVI时间序列重建。选取样本点和样区分析并比较不同滤波方法的滤波结果，并使用滤波后的结果进行植被分类，根据分类精度进一步验证不同滤波方法的滤波效果。

1 研究区和数据

1.1 研究区概况

南京地处长江下游的丘陵地区，中心位于31°56′N，119°14′E，海拔高度20m～448m，属北亚热带季风气候区，年平均气温15.1℃，年降水量1019mm。在自然地理组成上表现出几个明显特点：①由于地处长江下游，境内河流湖泊交错，湿地和水域面积广阔；②境内的低山丘陵起伏，局部地形复杂；③植被以落叶阔叶林和常绿阔叶林为主要成分，竹林等植被类型也比较常见；④本地区人口密集，属于人为活动强烈区，农田生态系统占有较大成分。自然植被在历史上屡遭严重破坏，几乎全部消失，现有植被多属次生性质，其中人工林面积大于自然恢复的次生林。南京市植被根据生态地理分布特点和外貌特征，分为落叶针叶林、常绿针叶林、落叶阔叶林、含常绿成分的落叶阔叶混交林、竹林及灌丛、草地等几个基本类型。从植被的特征和种类来看，该地区有较强的代表性。

1.2 数据及预处理

(1)遥感数据与预处理

本研究选用2013年全年HJ-1A/B卫星的二级数据产品，图层叠加、辐射定标后对数据进行裁剪，然后经过6S模型的大气校正和相对几何校正，几何校正的精度控制在0.2个像素之内，并将校正后的图像映射到UTM投影。筛选后剔除受云雾影响较为严重的图像，得到始于2013年1月2日以5天为时间间隔的73景图像序列。另外选用从美国航空航天局1级数据及大气数据档案数据库和分发系统获取的2013年全年的Terra星的MOD13Q1数据(带号h28v05，时间间隔为16 天的Level 3 植被指数数据)，并对数据进行重投影和几何校正以匹配HJ NDVI时间序列。

(2)地面实测数据

本研究针对不同的植被类型进行实地数据采集，获取纯植被像元点的经纬度信息，为滤波后效果的评价提供基础。具体实地考察路线及样本点分布情况见图1。

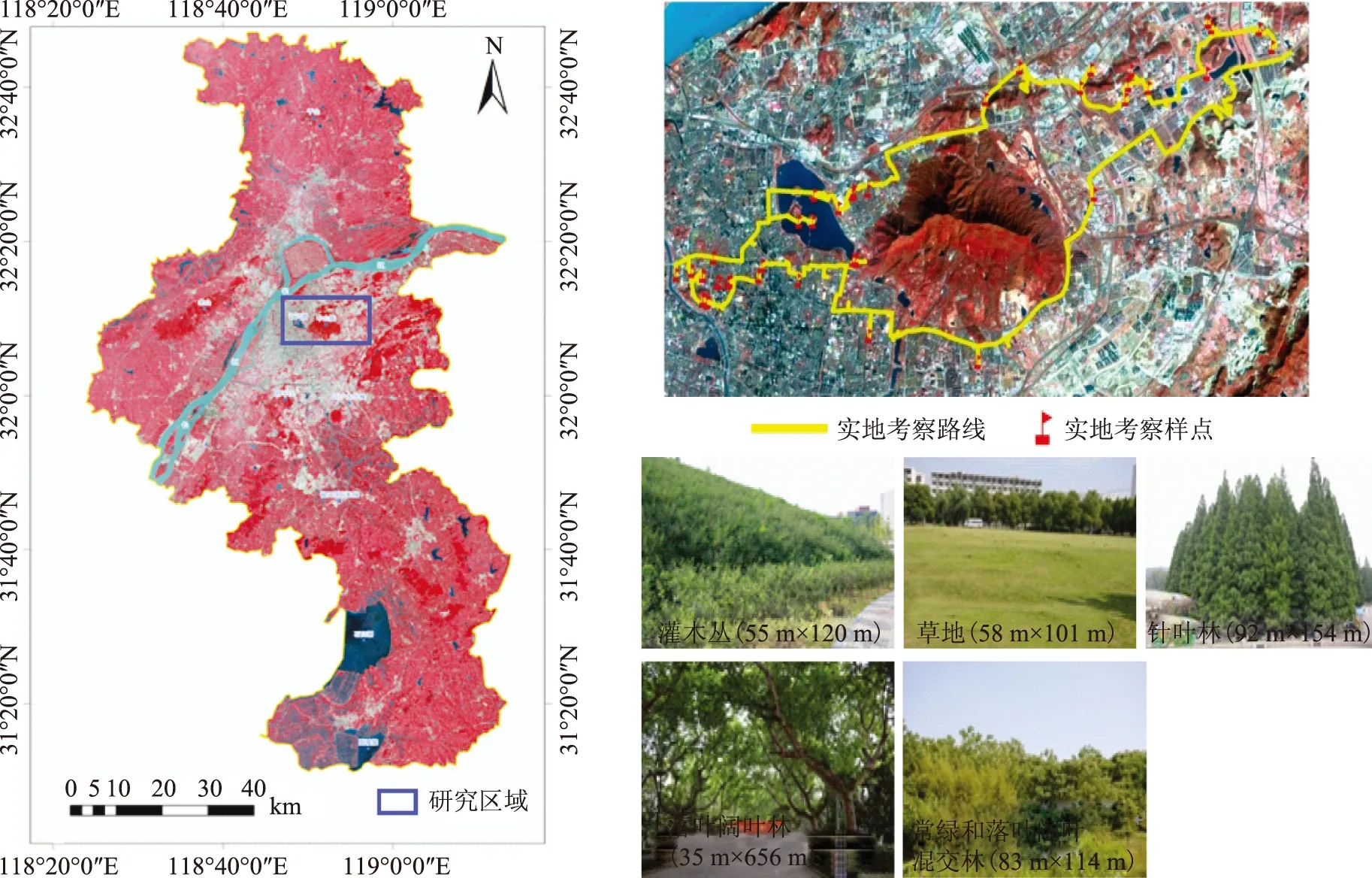
图1 研究区地理位置图、实地考察路线图及样本点实拍图

通过实地考察在研究区内确定5个纯植被像元点。结合遥感数据和各个像元点的天气记录情况，类比MODIS数据的QA评价数据，添加质量水平这一属性，质量水平越高，原始数据的信噪比越高，详细信息见表1。

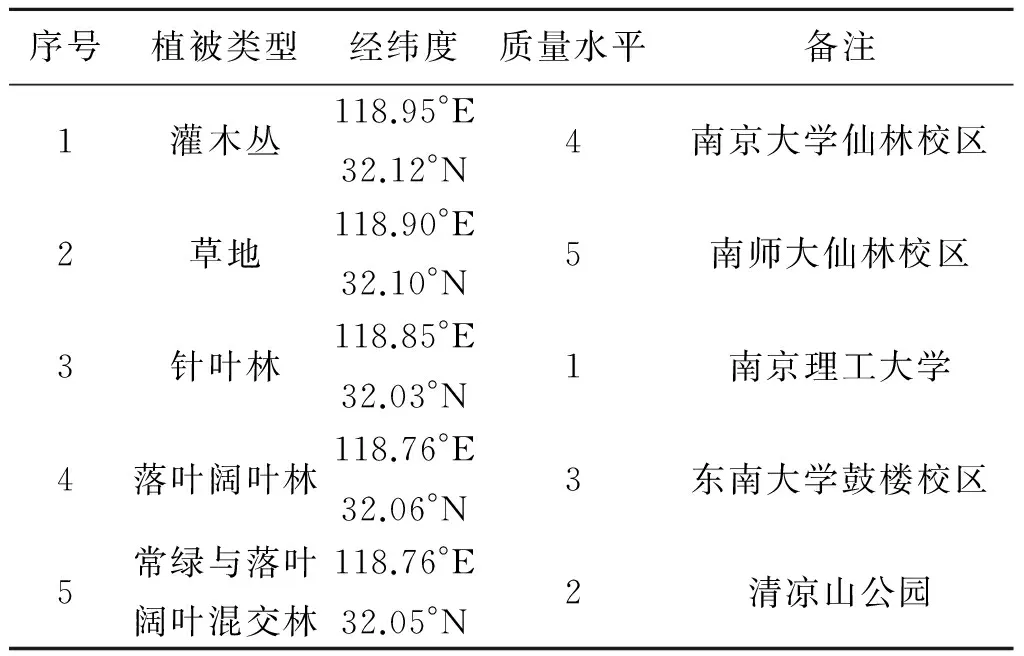
表1 纯植被样本点的基本信息

2 研究方法

本研究选取S-G滤波、AG拟合法、DL拟合法和Hants 4种滤波算法进行实验。其中S-G滤波、AG拟合法和DL拟合法可通过TIMESAT软件[14]对数据进行处理和实验。

2.1 S-G滤波

S-G滤波是Savitzky和Golay于1964年提出的一种应用最小二乘卷积拟合方法来平滑和计算一组相邻值的函数[12-13]。它使用一定大小的滑动窗口对待处理数据进行卷积运算，并对待处理数据进行多项式拟合。该方法的基本公式如下：

(1)

式中，Y为原始的NDVI时间序列，Y*为滤波后的NDVI时间序列。m为一正整数，2m+1代表了滑动窗口的大小，N为卷积数，数值上等于滑动窗口的大小。Ci为第i个NDVI 值带入滤波计算时的系数。这种算法在TIMESAT中主要需要用户控制两个参数控制滤波效果，一个是滤波窗口大小，二是平滑多项式的次数，较低的次数可以得到更平滑的结果，但会保留异常值，高的次数可以去掉异常值但又过分拟合，引起新的噪声[14]。

S-G滤波法的特点是能够细致描述序列的长期变化趋势，并在滤去噪声的同时尽量保持细节信息。但由于其本质还是一种滑动平均，所以在噪声比较多的情况下不能得到单调、光滑的时间序列曲线。

2.2 AG拟合法

AG拟合法是基于非线性对称高斯函数的最小二乘法拟合时间序列模型。最早由Peter Jönsson和Lars Eklundh在2002年提出[8]。其过程分为局部拟合、参数确定和全局拟合3个步骤[15]。

非对称高斯函数拟合法能够高度概括植物生长模式，得到的时间序列曲线光滑、单调，但是很容易忽略序列变化的细部信息，产生过度概括现象。

2.3 DL拟合法

DL拟合法是由Beck等[10]于2006年提出的一种新的算法，与非对称高斯滤波函数类似，双逻辑函数滤波也是一种局部拟合函数，它们具有相同的基本公式。它首先将整个时间序列中时间点对应的数值按极大值或者极小值分成若干个区间，然后分别对各个区间进行双重逻辑函数局部拟合。其处理过程和AG拟合法类似。

Beck[10]在其文章中指出，相比于基于傅立叶变换的滤波算法，双重逻辑函数滤波对植被生长季的估计更加准确，特别对高纬度地区此算法更加适用。

2.4 Hants

Hants是一种新的物候分析方法，其核心算法是傅里叶变换和最小二乘法拟合，Hants算法对快速傅里叶算法进行了改进，它不仅可以去除云的噪声点，而且对时序图像不要求等间隔性，有更强的灵活性。

Hants算法的全部过程中涉及到的参数较多，其中最为重要的参数有拟合周期、频率数、拟合误差容限和有效值区间。与其他基于傅里叶的分析方法相同，以上参数需要不断尝试才能获得最佳值[16]。Hants的优点在于，它能够光滑地反应植被生长曲线，并可根据用户意图，调整拟合结果地物物相变化周期规律的概括程度。

2.5 滤波参数

以上4种方法可以视为是3种基本原理不同、应用场景各异、重建效果各具特色的时间序列重建方法(其中AG拟合法和DL拟合法原理相近，可以归为一种)。由于S-G滤波在滑动窗口大小的选择上针对不同数据需要进行不同设置，本研究选用两种滑动窗口大小分别为3和5的S-G滤波进行实验，得到5种不同的滤波结果。经过大量测试，针对本研究区，选取滤波效果相对较理想的参数组合进行4种滤波方法重建效果的比较，参数设定如表2所示。

2.6 滤波效果评价方法

本研究选用了NDVI均值、NDVI平均绝对误差和相关系数3个统计量用于对样点滤波效果评价。各统计量设计如表3所示。

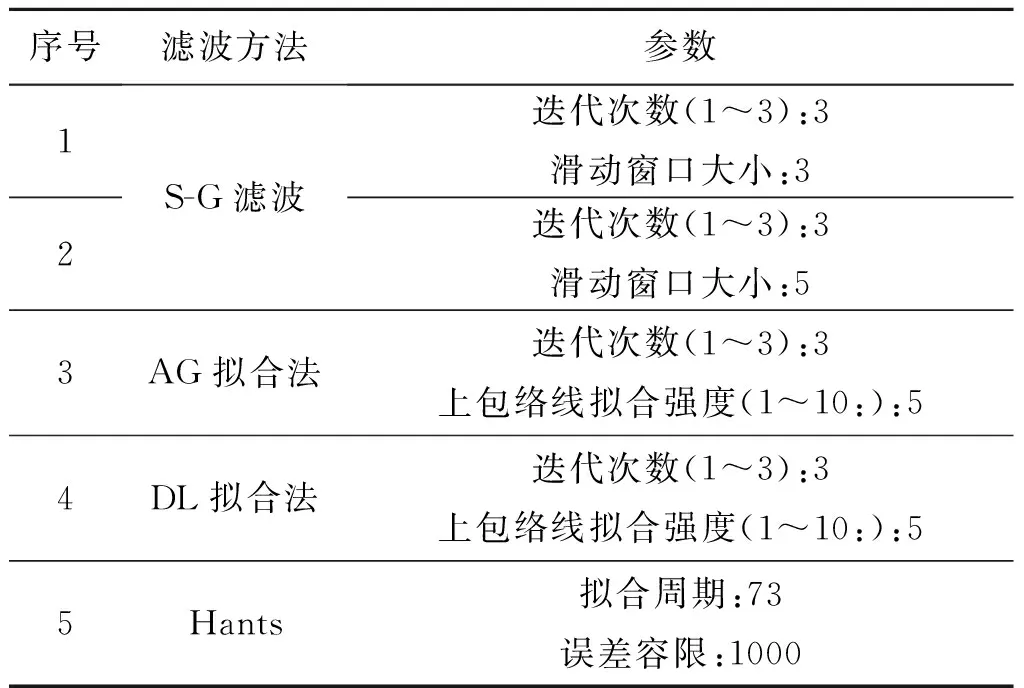
表2 HJ NDVI时间序列滤波方法参数设定

表3 定量分析的统计量计算公式和相关说明

此外，由于研究城市植被HJ NDVI时间序列的下一步工作是实现城市植被分类，因此滤波效果除了根据以上的统计量进行评判，还应考虑滤波后的NDVI时间序列是否可以实现城市植被分类，本研究将滤波后的73景NDVI时间序列数据看作高光谱数据，并进行主成分变换，对主成分变换后的滤波结果选用最大似然法，进行监督分类，并求得误差矩阵，通过比较分类误差大小，进一步对比4种滤波方法对HJ NDVI时间序列的滤波效果。

3 滤波结果与分析

3.1 纯植被样本点滤波结果分析

由于常绿落叶阔叶混交林中的落叶阔叶林在春季发芽，秋季树叶开始老化、掉落，同时常绿阔叶林树木叶片中叶绿素含量也会随着季节更替而发生变化，使得NDVI时序曲线出现先增大后降低的趋势，因此选用常绿与落叶阔叶混交林的纯像元进行滤波结果分析，但由于HJ卫星数据本身的质量问题，造成HJ NDVI时间序列曲线出现双峰现象。如图2(a)和图2(b)所示，原始HJ NDVI时间序列经过S-G、AG、DL滤波后均有明显升高，而Hants处理过的HJ NDVI时间序列没有明显升高，如图2(c)所示。对比滤波后的光滑程度，Hants得到的结果最为光滑，AG和DL拟合法次之，S-G滤波的平滑效果最差。

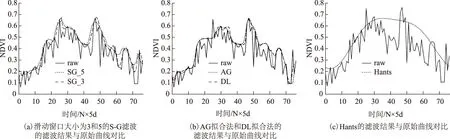
图2 常绿与落叶阔叶混交林样本点的5种滤波方法的滤波前后曲线

4种滤波方法都能一定程度上剔除异常值，但S-G滤波受异常值的影响最大，当噪声点较多时较容易出现滤波后曲线随着异常曲线波动的情况，且滑动窗口越小受影响的程度就越大，AG、DL拟合法次之，Hants最小。虽然Hants可以消除HJ NDVI时间序列的双峰现象，但Hants的滤波结果会在一定程度上降低HJ NDVI时间序列的峰值，并且由于较大的平滑力度，会削弱HJ NDVI时间序列中包含的植被物候特征信息。

通过对4种滤波方法均值进行对比，5种纯植被像元点NDVI值均有升高，其中滑动窗口大小为5的S-G滤波法对原始NDVI值的升高效果更为明显。此外，所有滤波结果对乔木、灌木、草本植物的NDVI值升高幅度呈现递减，其中对针叶林、落叶阔叶林、常绿与落叶阔叶混交林、灌木丛、草地的升高幅度分别为16%、14%、14%、12%、9%，如图3所示。乔木的NDVI均值在正常情况下大于灌木和草地，而噪声的大小并不随着NDVI值的大小而发生变化，所以原始NDVI值越大，噪声与其偏差的绝对值就越大，由于各个算法的结果都是不同程度地去除受地面水分或冰雪覆盖以及大气云层、气溶胶影响造成的NDVI值降低的情况远多于“假”高值的情况[1]，因此乔木、灌木、草本植物的NDVI均值升高幅度递减。

对比5种植被类型滤波结果与原始NDVI的平均绝对误差，AG拟合法和DL拟合法的平均绝对误差较为稳定，而S-G滤波和Hants不稳定，如图4所示。Hants滤波结果的平均绝对误差较大，原因是Hants本身的平滑力度较大。滑动窗口大小为5的S-G滤波后的平均绝对误差随着样本点的质量水平的提高而减小。

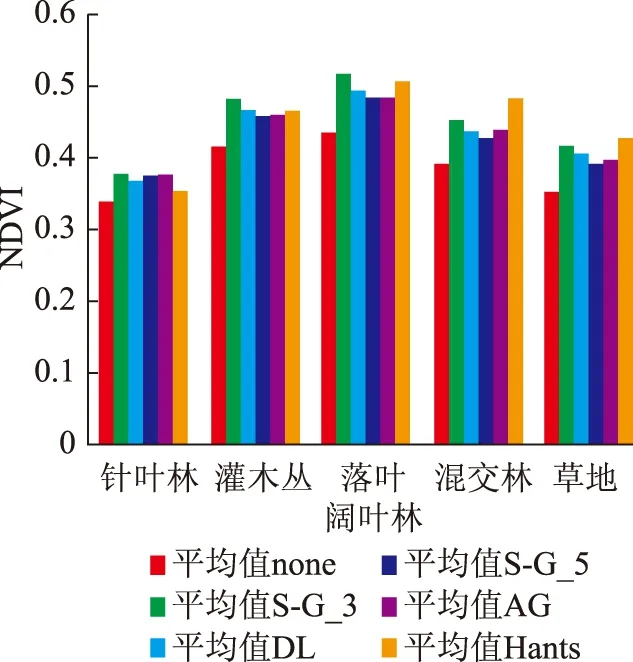
图3 5个纯植物样本点滤波后与原始数据平均值统计图

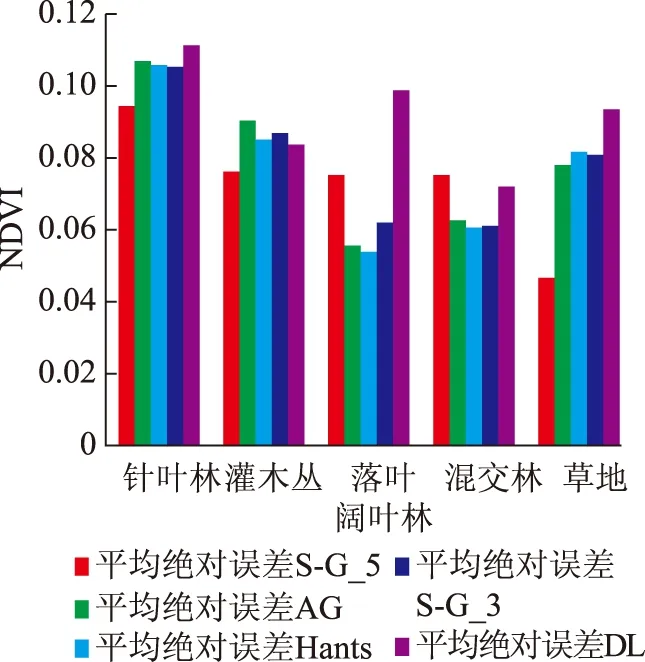
图4 5个纯植物样本点滤波后平均绝对误差统计图

图5 5个纯植物样本点滤波后与原始数据的相关系数统计图

5种滤波结果与原始数据的相关系数都大于0.78，70%可以达到0.85以上，如图5所示。结合样本点的质量水平，随着样本点质量水平提高，各种算法对原始高质量点拟合结果与原始值间的相关性都逐渐提高[2]。在本研究中，滑动窗口大小为5的S-G滤波的滤波结果随样本点质量水平的提高，相关性增大。

3.2 样区滤波结果分析

除对比纯植被的样点外，在研究区中植被覆盖度较高的区域随机选取了600m×600m的样区进行滤波效果对比。 如图6(a)所示，滑动窗口大小为3的S-G滤波虽然去除了部分噪音，但在第50景之后较明显的波动并没有得到弱化；对比滑动窗口大小为5的S-G滤波的滤波结果和原始曲线，大部分噪音得以去除，且滤波后的曲线平滑度较高，50景之后较明显的波动也得到弱化；AG和DL拟合法由于原理相似，滤波结果的波形十分相近，这两种方法与滑动窗口大小为3的S-G滤波相似，对50景之后较明显的波动的平滑效果也较差，DL拟合法滤波结果的平滑度大于AG拟合法，如图6(c)和图6(d)所示；Hants滤波结果的波形与前4种相比差异较大，波形十分平滑，但失去了原始曲线的细节特征，如图6(e)所示。

3.3 植被分类结果分析

基于植被分类的滤波结果分析首先将5个含有73个波段的滤波结果看作5个高光谱的多维图像，进行主成分变换，选取信息量最大的前3个波段进行分类，根据5类植被及其位置进行训练区选择，分类结果如图7所示。由于本研究的主要目的是对比滤波方法，在分类时只关注相对误差，不考虑绝对误差，5种分类结果的误差统计图如图8所示。所有的滤波方法与原始数据相比，分类精度均有提高，其中滤波窗口为5的S-G滤波表现出了最高的分类精度，其余依次是滤波窗口为3的S-G滤波、AG拟合法、DL拟合法和Hants。

3.4 滤波结果可靠性分析

为了验证滤波结果的可靠性，本研究选用2013全年以16天为间隔的23景MODIS NDVI时间序列数据来验证滤波结果的可靠性。由于HJ NDVI时间序列和MODIS NDVI时间序列时间分辨率的差异，本研究从HJ NDVI时间序列中选取23景与MODIS NDVI时间序列获取日期尽量重叠(误差小于等于3天)的HJ NDVI时间序列数据进行相关性检测，检测结果如图9所示。

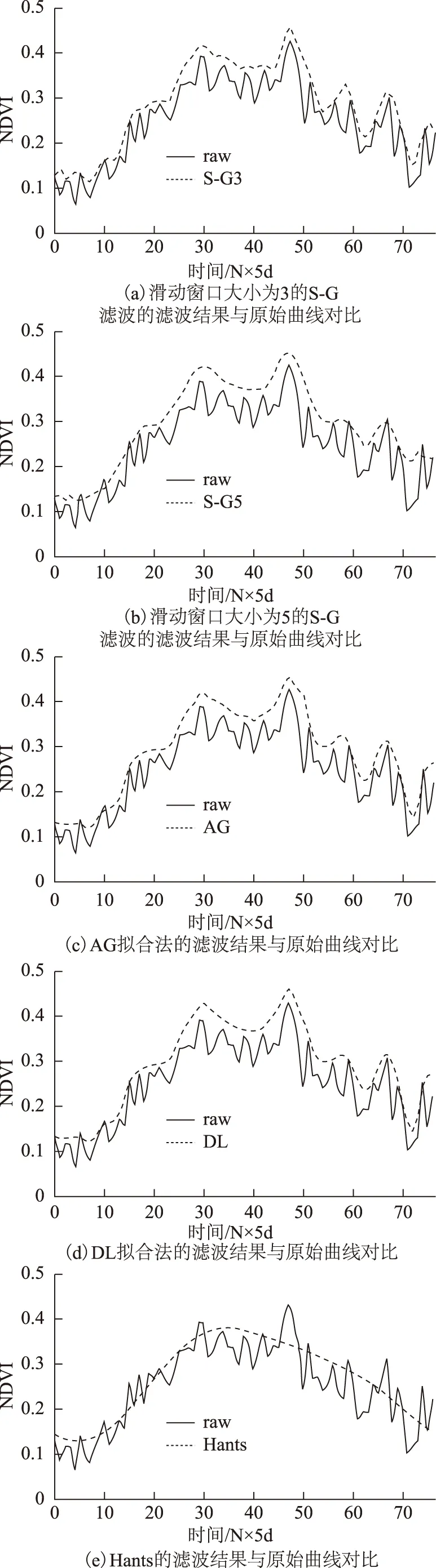
图6 五种滤波方法滤波前后样区内所有像元平均值的HJ NDVI

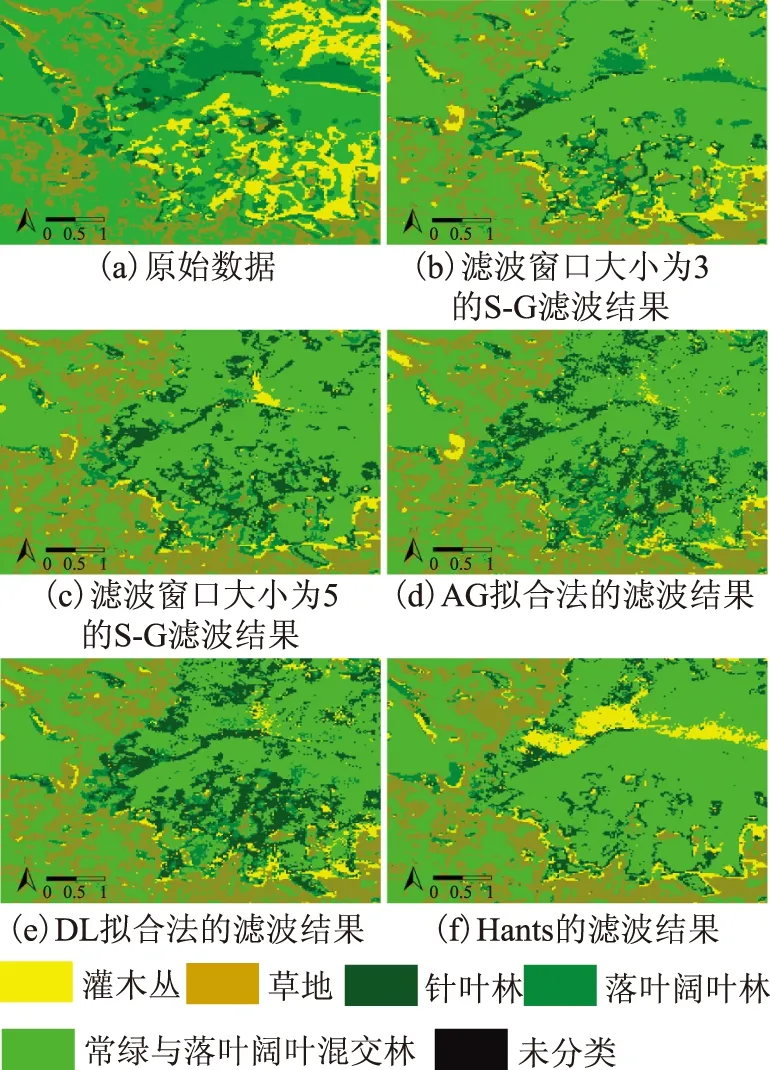
图7 5种滤波方法的最大似然分类结果图

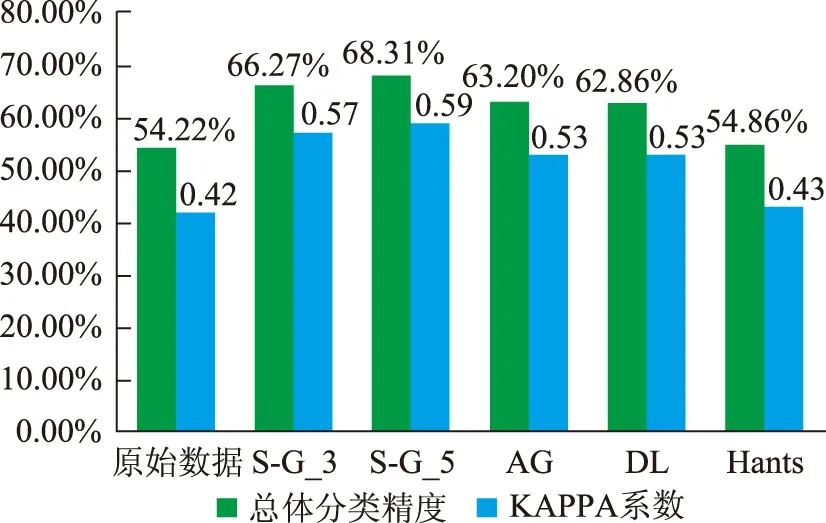
图8 5种滤波结果的最大似然分类结果精度统计图

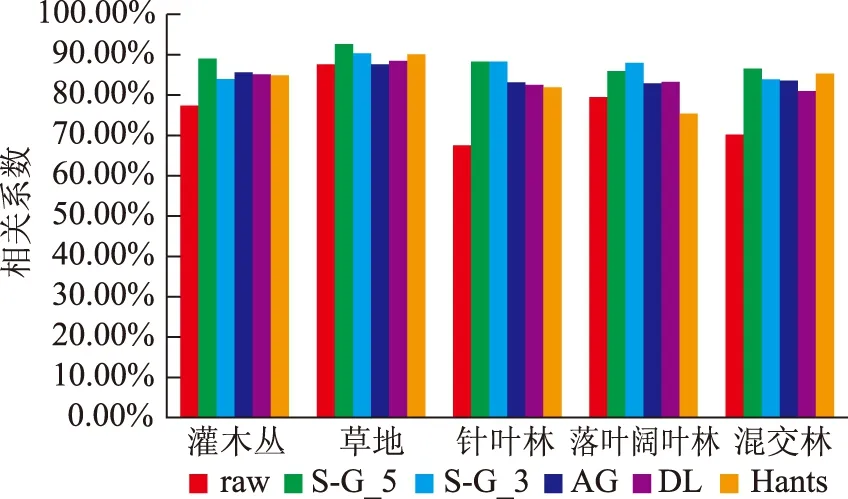
图9 原始数据和5种不同滤波方法滤波后的结果与MODIS NDVI时序数据的相关性检测结果统计图

统计图中的结果显示，虽然5种滤波结果都使原始数据与MODIS NDVI时序数据的相关性有所提高，但是滤波窗口为5的S-G滤波在针对5种不同的植被进行滤波时表现较为稳定，与MODIS NDVI时序数据均达到了85%以上的相关性，并对原始数据在其与MODIS NDVI时序数列相关性较差时(小于80%)都有了显著的提升(大于等于10%)，在5种滤波方法中显示出最高的可靠性。在图9中可以还看到，在原始数据质量较高的情况下(本研究中的草地)，5种滤波方法滤波效果的质量都会比原始数据质量较低时有所提高，但不会无限接近100%，在本实验中最高值是93%。

4 结束语

本研究通过对不同质量水平滤波前后纯植被样本点和样区的比较得到如下结论：①由于噪声会造成原始曲线NDVI值的降低，4种(两种不同滑动窗口大小的S-G滤波算法作为同一方法)滤波方法得到的结果均使原始NDVI值升高，其中滑动窗口大小为5的S-G滤波升高幅度最大；②AG与DL拟合法和滑动窗口大小为3的S-G滤波的滤波结果与原始曲线的相关性近似，且都高于滑动窗口大小为5的S-G滤波和Hants的滤波结果，前者更能体现出原始植被生长曲线特征；③Hants的滤波结果在波形上与其他方法明显不同，弱化了原始曲线应有的物候特征；④滤波后分类的结果中显示滑动窗口大小为5的S-G滤波有最高的精度，其余是滤波窗口大小为3的S-G滤波、AG拟合法、DL拟合法和Hants。经过综合比较，在本研究中滑动窗口大小为5的S-G滤波为最优的滤波方法；⑤与MODIS NDVI相关性测试中显示：滤波窗口大小为5的S-G滤波显示出最高的可靠性。

通过比较这4种算法，AG拟合法和DL拟合法从原理到滤波效果的各个方面都存在较大的相似性，在本研究中滑动窗口大小为3的S-G滤波得到和AG、DL拟合法相近的滤波结果，因此可以将AG、DL拟合法创造性地看作是较小滑动窗口的S-G滤波。Hants虽然可以得到平滑度最高的滤波结果，但是这种算法对原始曲线的细节保留很少，会造成原始NDVI曲线物候特征的损失。S-G滤波可以根据NDVI时间序列的长短选择不同的滤波窗口，较小的滤波窗口保留细节的能力更强，但细节保留的同时也带来噪声保留，较大的窗口可以得到更加平滑的滤波结果，但是太大的滤波窗口会使NDVI曲线失真，因此S-G滤波窗口大小的选择需要针对不同的数据反复试验，得到最优结果。

同时在研究中发现，由于HJ卫星缺少类似MODIS的QA评价数据，难以实现滤波结果的直接有效评价。因此，对具有较高可信度的HJ星QA评价数据的生成和HJ星的NDVI数据与MODIS NDVI数据的关系算法有待进一步研究和测试，以便提高HJ NDVI时间序列滤波结果的可信度。

[1] ACKERMAN S A，STRABALA K I，MENZEL W P，et al.Discriminating clear sky from clouds with MODIS[J].Journal of Geophysical Research，1998，103(32)：141-157.

[2] YU F，PRICE K P，ELLIS J，et al.Satellite observations of the seasonal vegetation growth in central asia：1982-1990[J].Photogrammetric Engineering & Remote Sensing，2004，70(4)：461-469.

[3] 汪业成.HJ卫星归一化植被指数时间序列的异常区段校正与物候期识别[D].南京：南京大学地图学与地理信息系统系，2014.

[4] 宋春桥，柯灵红，游松财，等.基于TIMESAT的3种时序NDVI拟合方法比较研究——以藏北草地为例[J].遥感技术与应用，2011，26(2)：147-155.

[5] VIOVY N，ARINO O，BELWARD A S.The best index slope extraction (BISE)：a met hod for reducing noise in NDVI time series[J].International Journal of Remote sensing，1992，13：1585-1590

[6] VERHOEF W.Application of harmonic analysis of NDVI time series(HANTS)[A].In Azzali S，MenentiM(eds).

[7] JÖNSSON P，EKLUNDH L.Seasonality extraction by function fitting to time-series of satellite sensor data[J].Geoscience and Remote Sensing，IEEE Transactions on，2002，40(8)：1824-1832.

[8] CHEN J，JÖNSSON P，MASAYUKI T，et al.A simple method for reconstructing a high-quality NDVI time-series data set based on the savitzky-golay filter[J].Remote Sensing of Environment，2004，91：332-344.

[9] SELLERS P，TUCKER C，COLLATZ G，et al.A global 10 by10 NDVI data set for global studies.Part 2：The generation of global fields of terrestrial biophysical parameters from the NDVI[J].International Journal of Remote Sensing，1994，15 (17)：3519-3545.

[10] BECK P，ATZBERGER C，HØGDAC K A，et al.Improved monitoring of vegetation dynamics at very high latitudes：a new method using MODIS NDVI[ J ].Remote Sensing of Environment，2006，100，321-334.

[11] JENNIFER N H，MCDERMID G J.Noise reduction of NDVI time series：an empirical comparison of selected techniques[J].Remote Sensing of Environment，2008，113 (1)：248-258.

[12] SAVITZKY A，GOLAY M J E.Smoothing and differentiation of data by simplified least squares procedures[J].Analytical Chemistry，1964，36：1627-1639.

[13] GU Z H.A study of calculating multiple cropping index of crop in China using SPOT/VGT multi-temporal NDVI Data[D].Institute of Resources Science，Beijing Normal University，2003.

[14] JÖNSSON P，EKLUNDH L.TIMESAT a program for analyzing time series of satellite sensor data：user's guide for TIMESAT 2.3[Z].Sweden：Malmöand Lund，2006.

[15] JÖNSSON P，EKLUNDH L.TIMESAT—a program for analyzing time-series of satellite sensor data[J].Computers & Geosciences，2004，30(8)：833-845.

[16] 李儒，张霞，刘波，等.遥感时间序列数据滤波重建算法发展综述[J].遥感学报，2009(2)：335-341.

Performance of Filters for City Region HJ-1A/B NDVI Time-series Analysis

LIU Han1，2，3，FENG Li1，2，3，ZHU Liu-jun1，2，3，HUANG Yin-you1，2，3

(1.JiangsuProvincialKeyLaboratoryofGeographicInformationScienceandTechnology，NanjingUniversity，Nanjing210023；
2.KeyLaboratoryforSatelliteMappingTechnologyandApplicationsofStateAdministrationofSurveying，
MappingandGeoinformationofChina，NanjingUniversity，Nanjing210023；
3.DepartmentofGeographicInformationScience，NanjingUniversity，Nanjing210023)

HJ-1A/B NDVI (HJ NDVI) time-series data possess relatively high spatio-temporal resolution.However，due to the restrictions of HJ satellite's imaging conditions and limits of the satellite platform，HJ NDVI time series are polluted by noises.Finding the most optimal filtering algorithm can be the key to solve this problem.This study introduced four kinds of filters including the asymmetric Gaussian fitting method (AG)，the double logistic curve fitting method (DL)，the Savitzky-Golay (SG) filtering method and the harmonic analysis of NDVI time-series (Hants).HJ NDVI time series of typical vegetation region in Nanjing city are established，and filtering experiments of the four filters are performed on them.Filtering results of the pure pixel sample points and the sample zones as well as the five typical vegetation's classification accuracy of the filtered data are compared to evaluate the performance of the four filters and finally MODIS NDVI tine-series data are included to test the reliability of the four filters.The results show that the S-G filter with a sliding window edge length of 5 has the best performance.Conclusions of this study can provide reference for filter selection of HJ NDVI time series based research.

urban vegetation；spatio-temporal resolution；HJ NDVI time-series；filtering；Nanjing city

2014―09―26

2014―12―11

国家自然科学青年基金(41301446)。

刘寒(1993—)，女，本科，研究方向为植被与生态遥感、全球变化。

E-mail：lh349796242@163.com

10.3969/j.issn.1000-3177.2015.05.011

TP79

A

1000-3177(2015)141-0069-08