利用直线特征进行有理多项式模型精度优化

伍洋，刘军，刘志龙，周俊明

(1.解放军信息工程大学地理空间信息学院，郑州 450052；2.中国天绘卫星中心，北京 102102)

利用直线特征进行有理多项式模型精度优化

伍洋1，刘军1，刘志龙1，周俊明2

(1.解放军信息工程大学地理空间信息学院，郑州 450052；2.中国天绘卫星中心，北京 102102)

针对控制点获取较困难地区有理多项式(RPC)模型定位精度不高的情况，提出了一种利用直线特征进行RPC模型精度优化的算法。该算法借鉴利用地面控制点进行RPC模型系统误差补偿的基本原理，通过对物方和像方直线特征的参数化表达，实现了基于直线特征的RPC模型系统误差补偿。利用该算法以及传统方法对资源三号(ZY-3)卫星影像进行实验。结果表明：在缺少地面控制点的情况下，利用直线特征对RPC模型进行精度优化是可行的；当地面控制线数量达到4条以上时，优化后RPC模型的定位精度可以达到与同等数量控制点相当的水平。

直线特征；RPC模型；物方补偿；像方补偿；资源三号

0 引 言

自从Space Imaging公司首次采用有理多项式(Rational Polynomial Coefficients，RPC)模型作为Ikonos卫星影像分发的几何模型以来，RPC模型在高分辨率光学遥感卫星影像的发布中被广泛采用。RPC模型的生成普遍采用的是“地形无关”的方式，即通过对严格几何模型的拟合得到[1]。因此，卫星星历、姿态数据的测量误差将会直接反映到RPC模型中，导致其存在明显的系统误差。可以通过引入地面控制点补偿RPC模型的系统误差，通常有两种技术方案，即物方方案和像方方案[2]。大量研究表明，极少量的地面控制点就可有效改善RPC模型的定位精度[3-4]。

现有的RPC模型系统误差补偿方案，所采用的控制信息都是基于实际的物理控制点，但是在很多情况下，这种实际控制点的获取比较困难，而线状特征数据相对来说获取较容易。目前，已有一些学者对线特征应用于高分辨率卫星影像进行了相关研究，如叶勤利用直线特征在物方对RPC模型进行系统误差补偿[5]，Teo研究了基于线特征的有理函数模型[6]，Shi和Al-Ruzouq利用直线特征进行高分辨率卫星影像配准[7-8]等，都取得了一定的成果。本文在这些研究的基础上，提出了利用直线特征进行RPC模型系统误差补偿的方法，对常规的像方和物方补偿模型进行了扩展，利用已知的控制线信息，提高RPC模型的定位精度，并利用ZY-3卫星影像进行了精度验证。

1 RPC模型及其系统误差补偿

1.1 RPC模型的定义

RPC模型的实质是有理函数模型，即将像点坐标与相应地面点空间坐标之间关系表示为一组多项式比值的模型，其定义为[4]：

(1)

其中，Nums(U,V,W)、Dens(U,V,W)、Numl(U,V,W)、Denl(U,V,W)都是如下形式的多项式：

p=a1+a2V+a3U+a4W+a5VU+a6VW+
a7UW+a8V2+a9U2+a10W2+a11UVW+
a12V3+a13VU2+a14VW2+a15V2U+a16U3+
a17UW2+a18V2W+a19U2W+a20W3

(2)

(U,V,W)是标准化后的地面点空间坐标(Latitude，Longitude，Height)，(s,l)是标准化后的像点坐标(sample，line)，ai是有理多项式系数，它们和标准化比例参数共同保存在卫星影像的辅助文件中。

1.2 RPC模型系统误差补偿方案

大量实验表明，高分辨率卫星影像的RPC模型都存在明显的系统性误差，需要利用一定数量的地面控制点对其进行补偿。主要有两种补偿方案，一种是在物方空间进行补偿，另一种是在像方空间进行补偿[3]。对于物方补偿方案，其实质是以RPC模型立体交会出的空间坐标为基础，通过对其进行某种变换来消除系统误差。具体的优化模型有多种。研究表明：平移补偿模型效果不佳；平移缩放补偿模型和仿射变换模型提高精度较多，所需控制点也较少[4]。像方方案则是通过引入像点坐标的低阶多项式描述RPC模型的定位误差，其中广泛采用的是仿射变换模型。

(1)物方补偿方案

童晓华将物方系统误差表示为[9]：

(3)

式(3)中，(XRPC,YRPC,ZRPC)是通过影像的辅助文件计算出来的RPC模型坐标，(X,Y,Z)是相对应点的地面坐标，ai,bi,ci是模型参数，根据不同的参数选择，有以下几种误差模型：

①a0,b0,c0：平移模型，优化效果不理想；

②a0,b0,c0,a1,b1,c1：平移缩放模型，需要两个控制点计算模型参数，a0,b0,c0对应误差的平移量，a1,b1,c1是比例因子，XRPC是产生误差变化的主要因子。对线阵推扫影像来说，影响其误差变化主要因素在沿平台飞行方向，因此对于近极轨遥感卫星影像其误差变化主要受纬度影响；

③a0～a3,b0～b3,c0～c3：仿射变换模型。

由于平移模型的优化效果不佳。本文将在平移缩放模型和仿射变换模型基础上进行基于线特征的RPC优化模型的相关公式推导。

(2)像方补偿方案

像方方案的实质是先消除像点坐标的系统误差，再利用修正后的像点交会出地面点，一般采用仿射变换公式对RPC模型误差进行修正：

(4)

式(4)中，(sRPC,lRPC)是实际地面点坐标通过RPC系数反算到像方的坐标，(s,l)是原始像点坐标，ai,bi是仿射变换参数。

2 基于直线控制的RPC 系统误差补偿模型

在传统的摄影测量处理中，都是利用物理意义上的点来解求式(3)、式(4)中的模型参数。基于直线特征的RPC误差补偿模型则将控制点(GCP)换成控制线(Ground Control Line，GCL)来进行处理。

理论上，对于线阵CCD推扫成像传感器而言，由于其行中心投影的特性，除非是匀速直线飞行且相机姿态不发生变化，否则物方的直线特征反映到影像上不再是直线。但对于航天摄影测量来说，由于卫星平台在高轨运行时受空间环境的干扰较小，又采用了惯性平台及地面跟踪观测等先进技术，卫星的姿态变化率很小，故由于轨道微小变化所引起的影像几何变形很小，物方直线在卫星影像上的对应特征仍可近似看作是直线[10]。实际上，地面直线在卫星影像上的成像特点也说明了这点。因此对于卫星线阵CCD 影像，利用物方空间的已知直线地物及其在影像上对应的直线特征进行定位参数的解算是可行的。

2.1 直线段的表达形式

直线的表达形式有多种：如利用两平面方程表示的空间直线的一般方程、直线的极坐标方程、直线的参数方程等。本文采用直线的参数方程建立模型，物方空间和像方平面直线的表达形式如式(5)：

(5a)

(5b)

式(5)中，(m,n,p)和(k,h)是直线的方向数，j、t是比例系数。

2.2 基于直线控制的物方补偿模型

(1)平移缩放模型

叶勤曾提出一种基于直线控制的RPC模型误差补偿方法[5]，在原有的物方误差补偿模型基础上，将控制点替换为控制线对RPC模型进行优化，其流程图如图1所示。

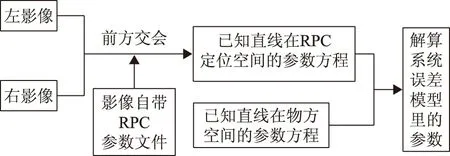
图1 基于直线控制的物方模型误差补偿过程

首先利用立体影像RPC模型前方交会，解算出直线两端点的地面坐标，得到其参数方程：

(6)

将式(5)所示的地面控制线已知的参数方程、式(6)所示的待定方程一起代入平移缩放模型，得到：

(7)

上式可改写为：

(X0-XRPC0)+mj=(mRPC+a1mRPC)j′+
a0+a1XRPC0

(8a)

(Y0-YRPC0)+nj=(nRPC+b1mRPC)j′+
b0+b1XRPC0

(8b)

(Z0-ZPRC0)+pj=(pRPC+c1mRPC)j′+
c0+c1XRPC0

(8c)

利用式(8a)和式(8b)消去j以后可以得到：

(nmRPCa1-mmRPCb1+nmRPC-mnRPC)j′+na0-
mb0+nXRPC0a1-mXRPC0b1-n(X0-XRPC0)+
m(Y0-YRPC0)=0

由此，可得到式(9a)和式(9b)：

nmRPCa1-mmRPCb1+nmRPC-mnRPC=0

(9a)

na0-mb0+nXRPC0a1-mXRPC0b1=
n(X0-XRPC0)-m(Y0-YRPC0)

(9b)

同理由式(8b)和式(8c)可得到式(10a)和式(10b)：

pmRPCb1-nmRPCc1+pnRPC-npRPC=0

(10a)

pb0-nc0+pXRPC0b1-nXRPC0c1=
p(Y0-YRPC0)-n(Z0-ZRPC0)

(10b)

式(9)和式(10)即为引入控制线后建立的观测方程，每一条控制线可以列出4个方程，因此理论上至少需要2条直线特征来解算a0,b0,c0,a1,b1,c1这6个补偿系数。

(2)仿射变换模型

将式(5)、式(6)代入式(3)，有：

(11)

上式可改写为：

(12)

同(1)中原理(消去j)，可得到：

nmRPCa1+nnRPCa2+npRPCa3-mmRPCb1-
mnRPCb2-mpRPCb3=0

(13a)

na0+nXRPC0a1+nYRPC0a2+nZRPC0a3-mb0-
mXRPC0b1-mYRPC0b2-mZRPC0b3=X0n-Y0m

(13b)

以及：

pmRPCb1+pnRPCb2+ppRPCb3-nmRPCc1-
nnRPCc2-npRPCc3=0

(14a)

pb0+pXRPC0b1+pYRPC0b2+pZRPC0b3-nc0-
nXRPC0c1-nYRPC0c2-nZRPC0c3=Y0p-Z0n

(14b)

理论上，解算这12个补偿系数至少需要3条非退化直线特征(不能在一个平面)，3条线特征可以列出12个方程，正好解12个系数，但在实际解算过程中，用3条直线特征进行解算时，往往会出现病态方程，导致无法解算出系数，因此一般至少取4条线特征进行解算。

2.3 基于直线特征的像方补偿模型

本文提出了一种基于直线特征的像方补偿方案。其具体原理是：首先根据RPC参数文件分别反算出物方直线在立体像对上的参数方程，再根据已知直线在像空间的参数方程分别解算补偿模型系数，利用补偿模型更新像点坐标后，对立体影像进行前方交会得到优化后地面点坐标。其补偿过程如图2所示。

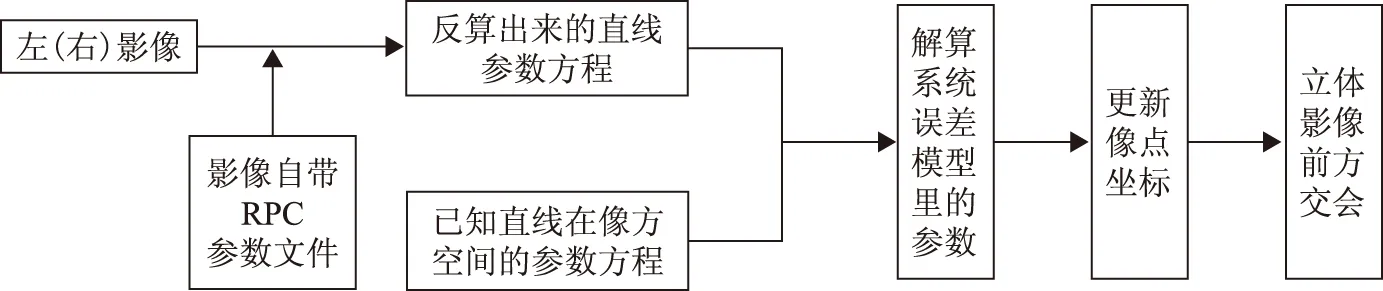
图2 基于直线控制的像方模型误差补偿过程

首先根据RPC参数文件反算出物方直线在像方平面的两端点，得出其在像方平面的直线方程如式(15)：

(15)

将式(15)和式(5)代入式(4)可以得到：

(16)

通过消元法(消去t′)得到：

(nRPCm·a1+nRPC·n·a2-mRPC·m·b1-
mRPC·n·b2)·t+nRPC·a0+nRPC·s0·a1+
nRPC·l0·a2-mRPC·b0-mRPC·s0·b1-
mRPC·l0·b2-(sRPC0·nRPC-mRPC·lRPC0)=0

(17)

由此，可得到式(18)：

(18)

通过该方程解算出模型的补偿系数以后，利用模型更新立体像对的像点坐标，再按照前方交会的方法解算出地面点坐标。对于该模型，未知数为6个模型参数，一条直线可以列出2个方程，所以利用该模型进行系统误差补偿至少需要3条非退化直线特征(不能在同一平面)。

3 实验与分析

3.1 实验数据

实验采用美国华盛顿地区ZY-3号卫星的前后视立体像对，影像大小为16300×16383，都附带有辅助RPC参数文件，其无控定位平面精度为15m，高程精度30m。实验中所采用的控制数据为该地区的矢量图(图3)，比例尺为1∶24000，其在影像中的分布范围(图4)，高程信息从分辨率为1°×1°的SRTM1数据获取，其标称精度为16m。

为验证本文的算法，本文根据实际地物特征(道路、地物边界线等)在影像和矢量图上人工量测了10条控制线，并量测了10个地面特征点作为检查点进行精度检核。

图3 华盛顿地区矢量图

图4 矢量图分布示意图

3.2 基于控制点的RPC模型优化结果

表1是利用控制点对RPC模型进行系统误差补偿的实验结果，3种模型所用的控制点数均为4个。

从表1可以看出，在采用4个地面控制点的情况下，平移缩放模型的精度与像方空间的仿射变换模型的精度大致相当或稍好，物方空间的仿射变换模型的精度低于这两者，3种方法的平面优化精度都高于其高程优化精度。

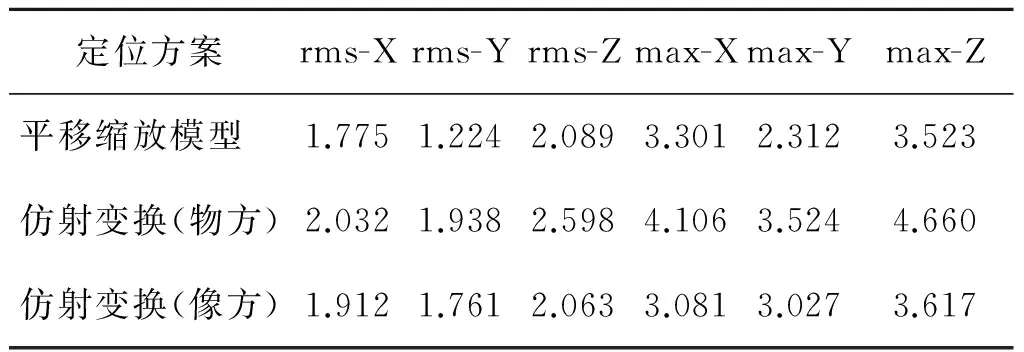
表1 基于控制点的RPC模型定位精度统计/m

注：表1中rms-X，rms-Y，rms-Z分别为X、Y、Z方向中误差，max-X，max-Y，max-Z分别为X、Y、Z方向最大绝对值误差(下同)。

3.3 基于直线控制的RPC模型优化结果

表2是利用量测的10条控制线对3种误差补偿模型进行实验的结果。

表2 基于控制线的RPC模型定位精度统计/m

3.4 结果分析

分析对比表1和表2，可以得出以下结论：

(1)对于平移缩放模型，基于线特征的补偿结果其精度与基于控制点的系统误差补偿方法的精度大致相当，基于线特征的补偿结果其平面精度要高于高程精度。

(2)对于物方空间仿射变换模型，与基于控制点进行解算的精度相比，基于线特征的解算精度要低，特别在线特征数目少时，这种差异较明显；在线特征数目小于10时，在同一套数据情况下，其补偿结果的精度比平移缩放模型和像方空间仿射变换模型差；线特征数目的增加对于精度的提升较平移缩放模型明显。

(3)对像方空间仿射变换模型，在控制线数目与控制点数目相等时，基于控制线的模型平面精度与基于控制点的模型平面精度持平，但是其高程精度低于基于控制点模型；其补偿精度比基于控制线的物方仿射变换模型的精度高；对于其自身而言，其平面精度要略高于高程精度。

4 结束语

RPC模型已经在高分辨率卫星影像的定位处理中广泛应用，技术已比较成熟，但大部分研究都是基于地面控制点来进行，而对于线特征用于摄影测量平差的研究却比较少。本文在以往研究的基础上，扩展了RPC定位的系统误差补偿模型，使其能够适用于直线特征，从而扩展了地面控制信息的选择范围。实验结果表明，利用直线特征进行RPC模型系统误差补偿是可行的，当地面控制线数量达到4条以上时，优化后RPC模型的定位精度可以达到与同等数量控制点相当的水平。本文实验过程中发现，线特征的空间分布以及其长度、角度等对补偿精度有不同的影响，其具体影响规律本文并未做研究，下步工作将对此进行研究。

[1] 刘军，张永生.基于RPC模型的高分辨率卫星影像精确定位[J].测绘学报，2006，35(1)：30-34.

[2] HU Y，TAO C V.Updating solutions of the rational function model using additional control information[J].Photogrammetric Engineering and Remote Sensing，2002，68(7)：715.

[3] 刘军，王冬红，基于RPC模型的IKONOS卫星影像高精度立体定位[J].测绘通报，2004，9(1)：1-4.

[4] 刘军，王冬红，刘敬贤.利用RPC模型进行IKONOS影像的精确定位[J].测绘科学技术学报，2006.23(3)：228-234.

[5] 叶勤，张小虎，刘世杰.基于直线特征的有理函数模型定位精度改善方法[J].同济大学学报(自然科学版)，2010，38(2)：295-301.

[6] TEO T，Line-based rational function model for high-resolution satellite imagery[J].International Journal of Remote Sensing，2013，34(4)：1355-1372.

[7] SHIWZ，SHAKER A.The line-based transformation model LBTM for image-to-imageregistration of high-resolution satellite image data[J].International Journal of Remote Sensing，2006，27：3001-3012.

[8] AL-RUZOUQ R.Data fusion of multi-source imagery based on linear featuresregistration[J].International Journal of Remote Sensing，2010，31：5011-5021.

[9] 童小华，刘世杰，叶勤.基于有理函数模型的QuickBird立体定位精度分析[J].同济大学学报 (自然科学版)，2009，37(4)：555-559.

[10] 张继贤，张永红，林宗坚.SPOT影像像点位移的研究[J].测绘科学，2000，25(1)：19.

Accuracy Optimization of RPC Model Based on Linear Features Control

WU Yang1，LIU Jun1，LIU Zhi-long1，ZHOU Jun-ming2

(1.InstituteofGeomatics，InformationEngineeringUniversity，Zhengzhou450052；2.TheCenterofSpaceSurveyingandMappinginChina，Beijing102102)

According to the principle of system error compensation of RPC model based on ground control points，this paper deduced RPC model system error compensation based on linear features in image space and object space by parametric expression of linear features，and carried out experiments by ZY-3 satellite images.The results show that it is feasible by using the straight line features for accuracy optimization of the RPC model when lack of GCPs.When the number of GCLs beyond 4，the accuracy can achieve the same level with equal number of GCPs.

linear control；RPC model；compensation in object space；compensation in image space；affine transformation

2014-06-30

2015-02-15

伍洋(1990—)，男，硕士研究生，主要研究方向为高分辨率卫星影像的定位技术。

E-mail：wuyang9527@163.com

10.3969/j.issn.1000-3177.2015.05.005

P236

A

1000-3177(2015)141-0031-06