模型参数不确定条件下的自主水下航行器(AUV)自适应编队控制研究*

李乐强 王银涛

(1.陕西省西安市79信箱19分箱 西安 710065)(2.西北工业大学航海学院 西安 710072)



模型参数不确定条件下的自主水下航行器(AUV)自适应编队控制研究*

李乐强1王银涛2

(1.陕西省西安市79信箱19分箱 西安 710065)(2.西北工业大学航海学院 西安 710072)

研究了自主水下航行器的编队控制问题,基于编队参考中心思想为每个AUV构造了期望参考轨迹。将每个AUV的系统误差分为自身跟踪误差和与邻居AUV的协同误差两部分,在此基础上,针对AUV模型参数不确定性,提出一种自适应分布式控制律,使得每个AUV沿着自身期望轨迹运动,并与相邻AUV保持同步,从而与编队参考中心保持期望的距离,达到编队控制的目的。文章基于Lyapunov稳定性原理从理论上证明了闭环系统的稳定性,仿真结果表明所提出的算法是有效的。

自主水下航行器; 编队控制; 分布式控制; 自适应控制

Class Number TP242

1 引言

目前,自主水下航行器(Autonomous Underwater Vehicle,AUV)的作业多以单个形式出现。随着任务复杂性的增大,仅通过单个AUV作业往往难以完成任务,此时需要通过多个AUV之间的合作和协调来完成任务。同时,通过AUV之间的合作和协调可以提高完成任务的效率以及整个系统的可靠性和鲁棒性。编队控制是多AUV协作中的一个典型性问题,也是研究其它协作问题的基础,它要求各AUV在执行任务时与队形中的其它AUV保持一定的空间距离。

编队控制在移动机器人、无人机以及航天飞行器等领域已取得了一定的研究成果[1～4]。从已有的文献看,主要有主从式编队控制、基于行为的编队控制以及基于虚拟结构的编队控制等三种编队方法。但相比上述研究领域及其编队控制方法,AUV由于自身复杂的动力学特性及其主要依赖水声通讯的作业环境,使得其编队控制面临更多的困难和挑战。文献[5]首先基于反馈线性化设计了路径跟踪控制器,之后基于同步梯度约束函数进行协同设计,实现了编队路径跟踪;文献[6]采用一致性算法与虚拟结构相结合研究了运动学层面的AUV小尺度编队控制问题;文献[7]则通过构造联系统实现欠驱动水面船对直线路径的协同跟踪,但其结果很难推广到一般的曲线路径。上述方法在控制律设计中,仅考虑了每个AUV的自身路径跟踪误差,而没有考虑与相邻AUV之间的位置误差,这样当编队参考中心发生故障时,整个系统有可能瘫痪。

本文针对AUV模型参数不确定,设计了一种适用于AUV编队的自适应控制律。在控制律设计中,考虑了AUV自身跟踪误差以及与其相邻AUV之间的距离误差,从理论上证明了算法的稳定性及参数收敛性,达到了编队控制的目的。

2 问题描述

2.1 AUV编队模型

考虑由n个AUV组成的编队系统,其中第i个AUV的运动学及动力学模型可以描述为[8]

(1)

(2)

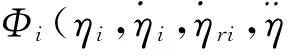
本文基于文献[5]中的编队参考点(Formation Reference Point,FRP)思想为每个AUV设定期望轨迹,如图1所示,其中ηd(t)为编队参考中心的期望轨迹,oi(t)为每个AUV相对于参考中心的期望编队向量,则每个AUV的期望轨迹可以表示为

ηdi(t)=ηd(t)+R(Ψd)oi(t)

(3)

式中,Ψd(t)为参考中心相对于惯性坐标系的姿态向量,R(Ψd)为参考中心坐标系到惯性坐标系旋转矩阵。

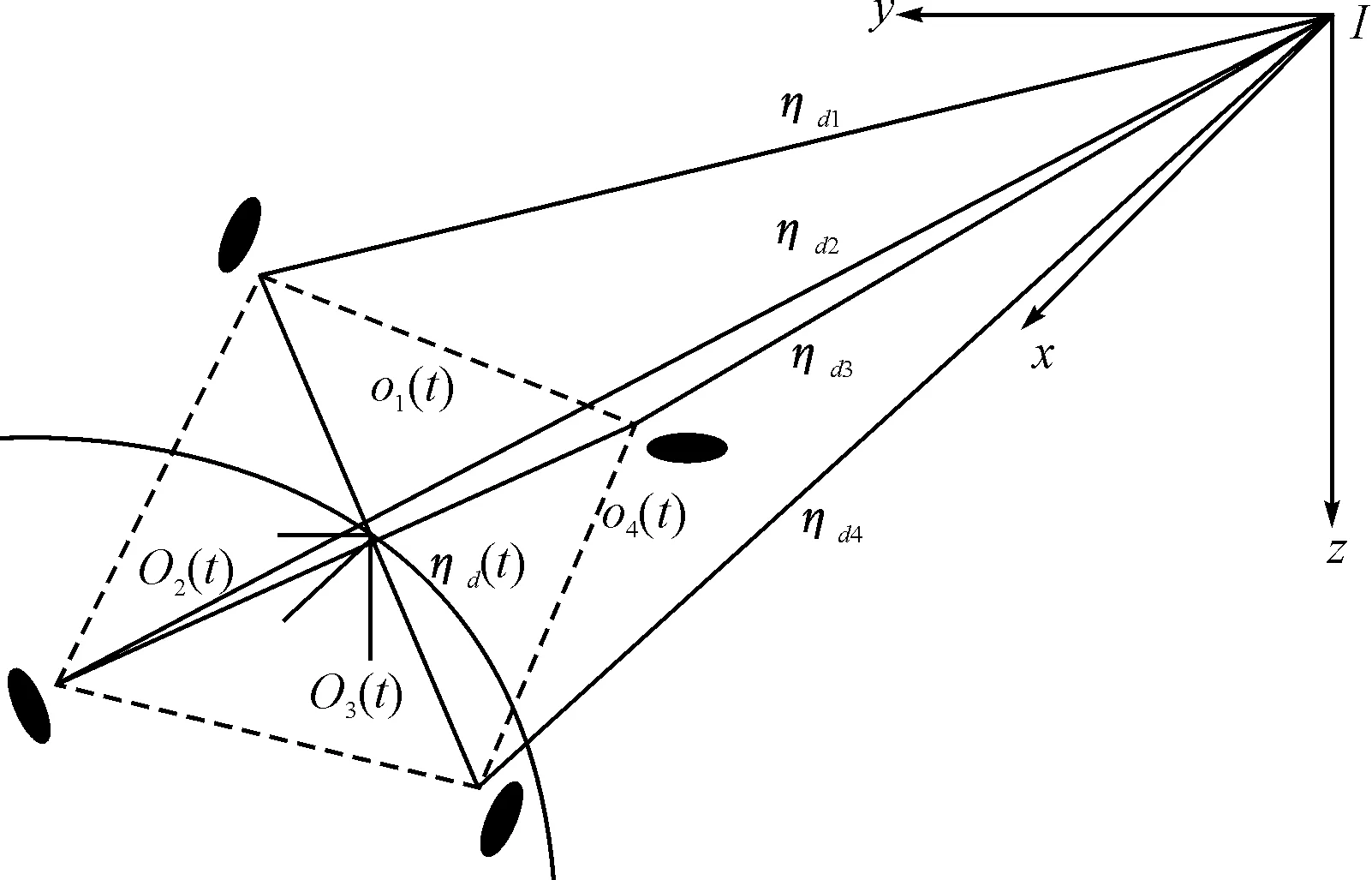
图1 编队跟踪示意图

2.2 控制目标

在上述知识的基础上,首先定义第i个AUV的轨迹跟踪误差为

(4)

i和j之间的协同误差定义为

(5)

在式(4)～式(5)的基础上,对于i个AUV,其系统误差可以表示为

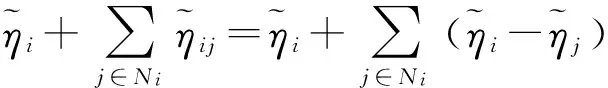
(6)

为保证每个AUV与参考中心速度上的同步,定义如下辅助变量:

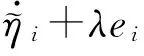
(7)

在上述定义的基础上,编队控制目标可以表示为

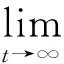
(8)

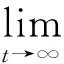
(9)

其中,式(8)为轨迹跟踪误差目标,保证每个AUV收敛到自身期望轨迹并与相邻AUV保持期望的相对位置;式(9)为速度跟踪目标,保证每个AUV在速度与邻居及其参考中心保持同步。

3 控制律设计

对于由n个AUV组成如图1所示的编队构型,提出如下分布式自适应控制算法:

(10)

(11)

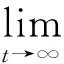
证明:由式(2)可知,存在参数不确定情形下,式(1)可以线性化表示为

(12)

将式(10)带入式(1)并利用式(7),式(12)有

(13)

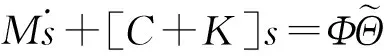
(14)

定义Lyapunov函数:

(15)

式中Λ=diag(Λi)。对式(15)进行求导有

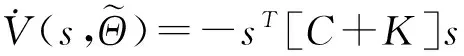
(16)

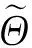
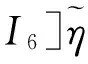
(17)

其中,⊗为Kronecker积。同理,对于s有

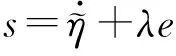
(18)

由式(17)～式(18)有

(19)

证毕。

4 仿真算例

为验证本文提出的编队跟踪控制算法,考虑六个AUV构成的编队系统,不失一般性,以水平面内AUV动力学模型为例,其模型参数请参见文献[8]。假定编队网络的通讯拓扑如图2所示。

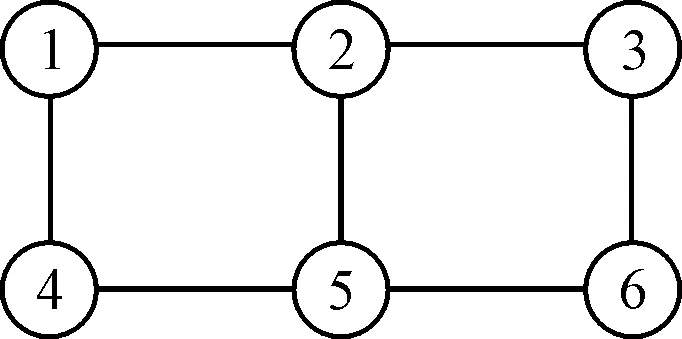
图2 通讯拓扑结构

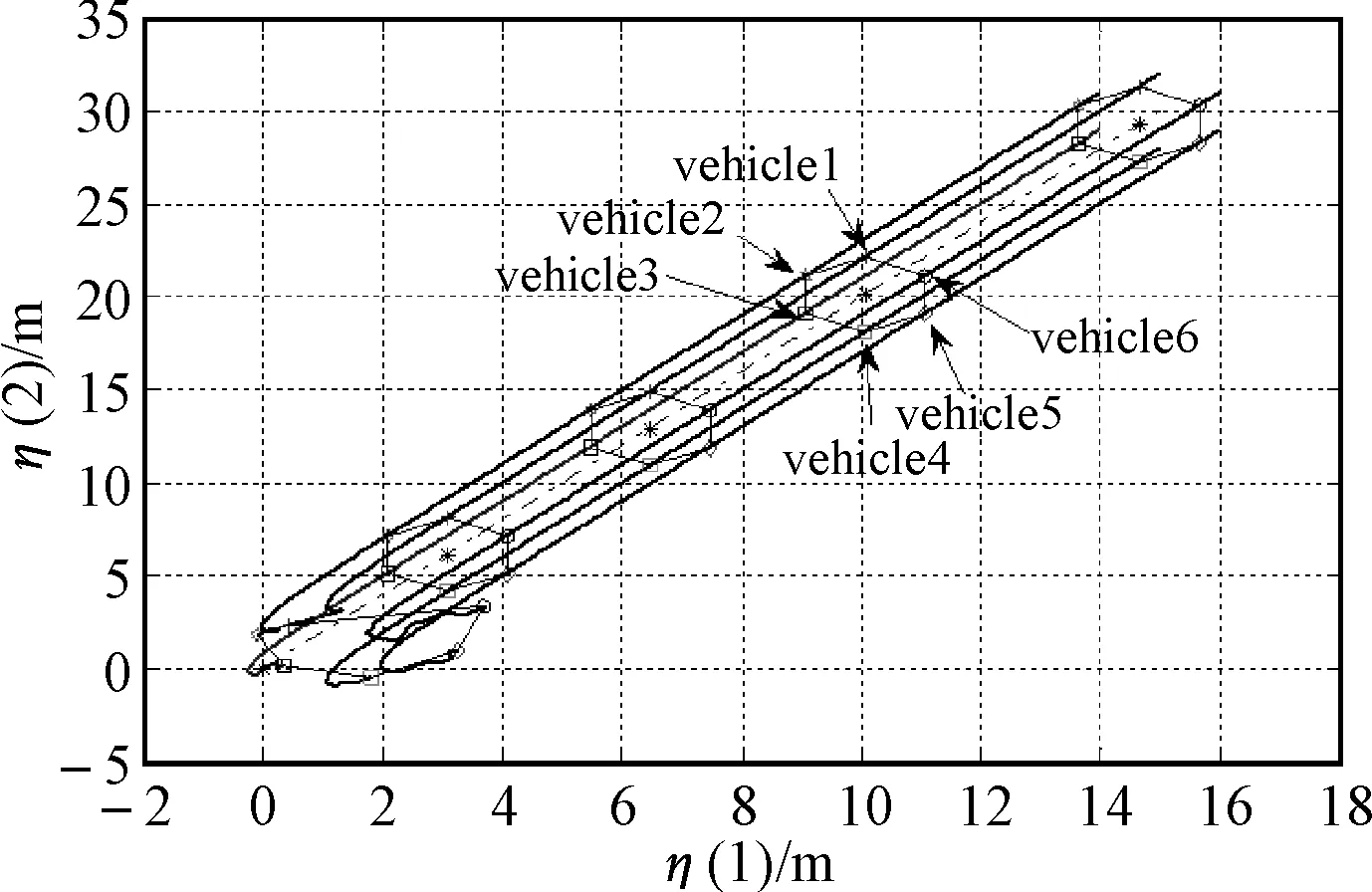
图3 编队轨迹曲线

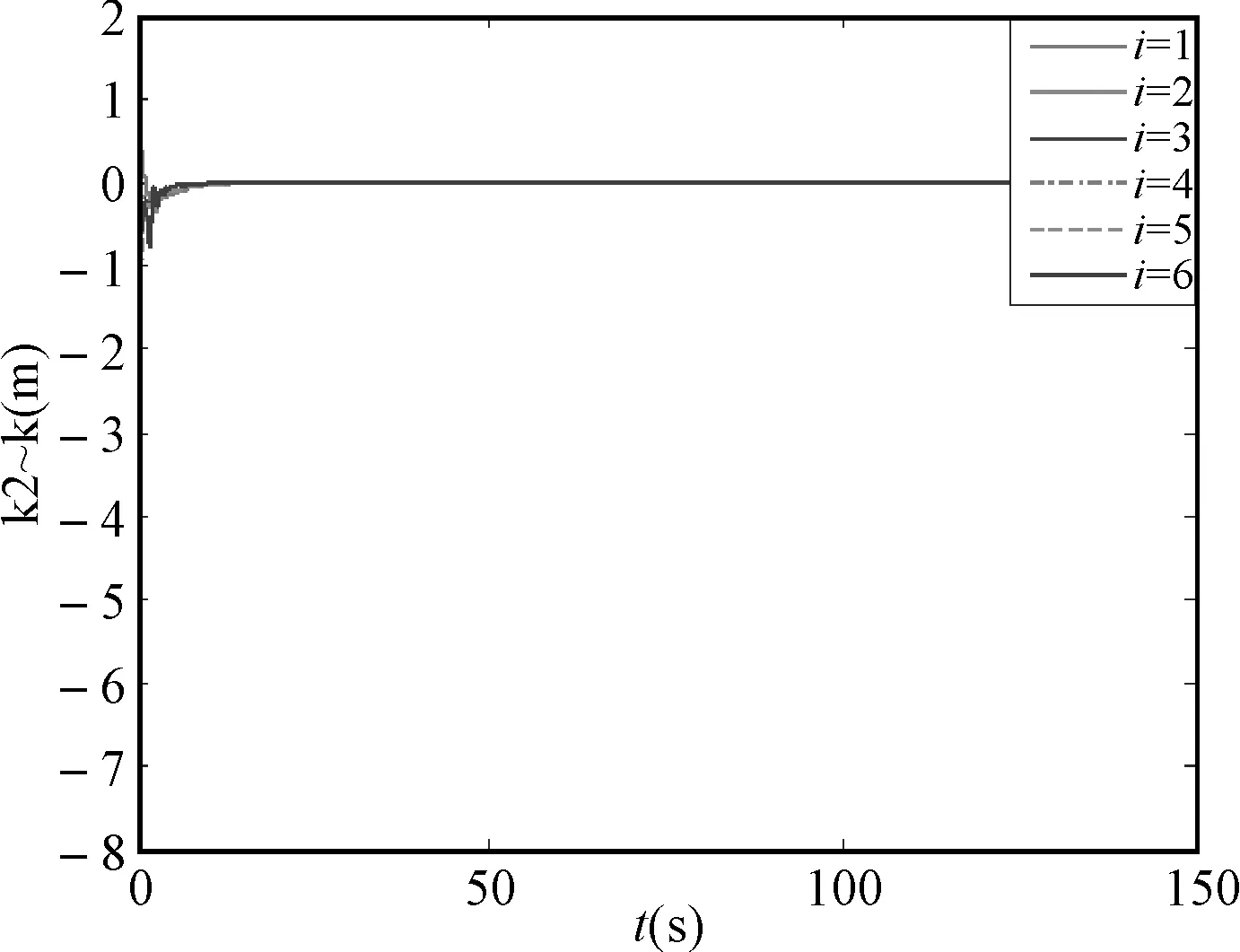
图4 轨迹跟踪误差曲线

仿真结果表明,各AUV能够与编队中心保持期望的队形运动,且各AUV系统的位置和速度能够实现对参考中心的协同跟踪。因此,文中提出的控制算法可以很好地解决当AUV模型存在参数不确定性时的分布式编队轨迹跟踪问题。

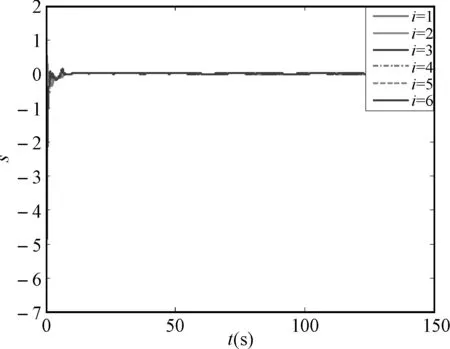
图5 误差变量s响应曲线

5 结语

论文基于编队参考中心的思想,根据编队参考中心的位置及航向信息为每个AUV构造了期望参考轨迹,并通过使AVU跟踪该轨迹来达到编队控制的目的。针对水下航行器的参数不确定性特点,设计了自适应控制律。可以看出,在AUV的控制器设计中,不仅考虑了每个AUV自身的跟踪误差,同时考虑了与相邻AUV之间的协同误差,这使得所有AUV能够同步地跟踪编队参考中心。此外,在模型参数自适应控制律的设计中均考虑了跟踪误差和协同误差,使得控制律能根据系统误差可以很好地进行自适应调整。文中编队参考中心的运动没有考虑AUV的信息状态反馈,如何利用AUV运动信息对参考中心进行控制是进一步研究的一个重要方向。

[1] A J Healey. Application of formation control for multi-vehicle robotic mine sweeping[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, Florida, USA,2001:1497-1502.

[2] W. Ren, N. Sorensen. Distributed coordination architecture for multi-robot formation control[J]. Robotics and Autonomous Systems,2008,56(4):324-333.

[3] 毕鹏,罗建军,张博.一种基于一致性理论的航天编队飞行器协同控制方法[J].宇航学报,2010,31(1):70-74.

[4] R. Ghabcheloo, A. Aguiar, A. Pascoal, et al. Coordinated path-following control of multiple underactuated autonomous vehicles in the presence of communication failures[C]//Proceedings of the 45th IEEE Conference on Decision and Control. San Diego, CA, USA,2006:4345-4350.

[5] I. A. F. Ihle, R. Skjetne, T. I. Fossen. Nonlinear formation control of marine craft with experimental results[C]//Proceedings of the 43th IEEE Conference on Decision and Control. Atlantis, Paradise Island, Bahamas,2004:680-685.

[6] 袁健,唐功友.采用一致性算法与虚拟结构的多自主水下航行器编队控制[J].智能系统学报,2011,6(3):248-253.

[7] E. Borhaug, A. Pavlov, K. Pettersen. Straight Line Path Following for Formations of Underactuated Marine Surface Vessels[J]. IEEE Transactions on Control Systems Technology,2011,19(3):493-506.

[8] Fossen T. Guidance and Control of Ocean Vehicles[M]. New York, USA: Wiley,1994.

[9] Royle G, Godsil C. Algebraic Graph Theory[M]. New York, USA: Springer Graduate Texts in Mathematics,2001.

[10] Khalil H K. Nonlinear Systems[M]. NJ, USA: Prentice-Hall,2002.

Adaptive Formation Control of AUVs in the Presence of Parametric Model Uncertainty

LI Leqiang1WANG Yintao2

(1. No. 79 Postbox 19 Brench, Xi’an 710065) (2. School of Marine, Northwestern Polytechnical University, Xi’an 710072)

In this paper, the formation control problem is studied for autonomous underwater vehicle, Based on the idea of reference center formation, the expected reference trajectory for each AUV is constructed. The system error of each AUV is divided into two parts for their collaborative error tracking error and the adjacent AUV. On this basis, according to the AUV model parameter uncertainty, an adaptive distributed control disciplinarian is proposed so that each AUV along its track desired trajectory, and keeps pace with the adjacent AUV, thus maintaining a desired distance and formation reference center, to achieve the purpose of formation control. It theoretically proves the stability of the closed-loop system based on the Lyapunov stability theory. The simulation results show that the proposed algorithm is effecite.

autonomous underwater vehicle, formation control, distributed control, adaptvie control

2014年7月10日,

2014年8月23日

李乐强,男,硕士,高级工程师,研究方向:海洋工程信号处理,自动控制。王银涛,男,博士,副教授,研究方向:水下航行器协同控制。

TP242

10.3969/j.issn1672-9730.2015.01.040