基于一维距离像的雷达目标识别*

李 飞

(92941部队92分队 葫芦岛 125001)



基于一维距离像的雷达目标识别*

李 飞

(92941部队92分队 葫芦岛 125001)

论文主要基于一维距离像研究了模式识别新技术在雷达目标识别中的应用,研究了一维距离像(HRRP)强度和平移敏感性,结合相对对准和绝对对准算法原理,对强度敏感性进行能量归一化处理,用滑动最大相关法进行目标识别。最后对各种功能及算法用C语言实现,并对最后的识别结果进行分析。

雷达目标识别; 一维距离像; 平移敏感性; 强度敏感性

Class Number TN957

1 引言

雷达目标识别指用雷达设备获取目标的特征信息(回波),并利用已掌握的各种目标的先验知识,判别未知目标的类别属性。因为各种形式的噪声和杂波严重污染了雷达回波中有用目标信息,而且即使在无噪声条件下,回波信号本身也往往不能包含足够的信息使问题有确定的解。因而从雷达回波中提取的目标信息通常是不完全的,由于这种不完全使得雷达目标识别问题成为一种广义逆的问题。雷达目标识别领域仍有大量的理论和实际问题有待解决。雷达目标识别是根据雷达目标回波进行的一种模式识别,因而也遵循模式识别的一般步骤,即包括信息获取、预处理、模式特征提取[1]及模式分类决策。

本文首先应用相对对准方和能量归一化的方法完成对雷达的一维距离像进行的预处理。然后采用等距抽样的方法对训练样本进行抽样,利用滑动最大相关法对目标进行识别,最后通过C语言实现运算,分析结果数据。

2 数据预处理

2.1 相对对准算法的原理

相对对准,可使用滑动最大相关系数准则来对准,其基本理论与滑动欧式距离相同。设样本空间的距离像为X1,测试飞机目标的一维距离像为X2,它们之间的滑动距离定义为X1,X2的所有循环移动的最小距离:

SED(X1,X2)=argmini‖SiX1-X2‖2,
i=1,2,…,d

(1)

式中,d为距离像单元数,算子Si为将向量石循环左移i个距离单元,(由此有SdX≡X)。因为

‖SiX1-X2‖2=‖X1‖2+‖X2‖2-2(SiX1)·X2

(2)

因此SED(X1,X2)等于使得相关系数

λ(i)=(SiX1)·X2

(3)

达到最大的X1和X2对准。

因为SED距离只能移动距离像单元数的整数倍,因此利用SED距离作相对对准只能是一种近似的不变变换。当然,如果距离像单元数越多,则近似程度越高。为了避免单元数的减少,使近似程度降低,本文在此决定直接采用一维距离像作为目标识别的特征,这样既避免了繁琐的处理,提取过程中可能的数据丢失,还能保证单元格的数量,提高近似程度。

2.2 强度匹配因子和能量归一化方法原理

2.2.1 强度匹配因子法

通常在目标识别中解决样本强度敏感性方法[2～3]就是摒弃样本的真实强度信息只利用形状信息。其中,具体的处理方法有两种:一是采用某种强度归一化方法,二是利用切空间的思想搜索最优的强度匹配因子。

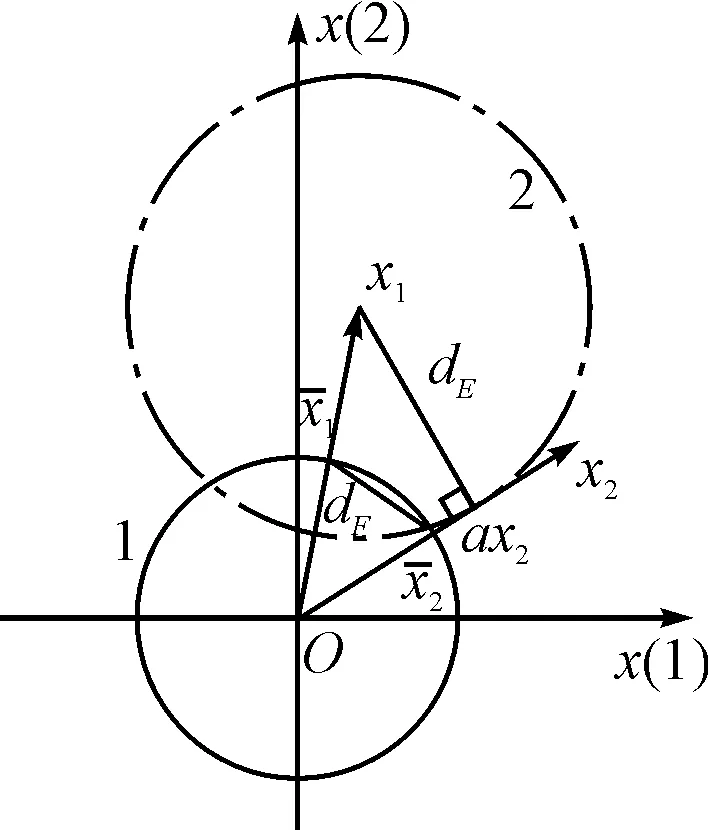
图1 二维平面内的欧氏距离示意图

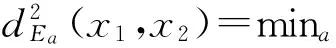
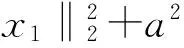
(4)

上式可以通过最小二乘法求解:

(5)

将式(5)代入式(4):

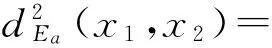
(6)

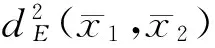
2.2.2 能量归一化方法

能量归一化的方法相对于最优强度匹配因子要简单很多,设未经能量归一化的一维距离像为xi,能量归一化后的距离像为xa,则有

(7)

由于高分辨距离像样本具有平移和强度敏感性[4],解决这两方面敏感性问题是雷达高分辨距离像目标识别预处理的基础。

3 距离像的目标识别

3.1 等距抽样法

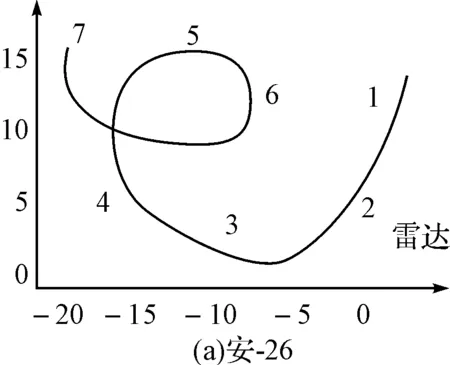
图2 三种飞机的平面行距

等距抽样[5～7]又称机械抽样或系统抽样,是事先将总体各单位按某一标志排列,然后按固定顺序和间隔来抽取单位构成样本,在等距抽样中用来排序的标志可以是无关标志,也可以是有关标志。采用等距抽样可以使样本单位较均匀的分布在总体中,有利于减少抽样误差,同时又具有方便经济的特点,因此在实际中广为使用。前面提到的将数据集按序号分成两类,序号为奇数的作为一类,序号为偶数的作为另一类即为等距抽样。实际数据分别是“安-26”、“奖状”、“雅克-42”飞机的一维距离像每种飞机针对其姿态敏感性问题分别分了5～7个阶段数据如图2。每个阶段数据有26000幅一维距离像,其经过FFT后所得一维距离像的像采样点数为256。对于每阶段的26000幅一维距离像真对其姿态敏感问题,取每阶段的一维平均距离像,即每隔100幅取一幅距离像,则在每个阶段平均一幅距离像所占的角度为0.014°,每隔100幅取一幅,相当于训练样本中每两幅距离像间的角度差为0.14°,根据微积分原理,可以认为在该小角度范围内的姿态不敏感。

3.2 滑动最大相关系数的识别方法的基本原理

滑动最大相关法实际上是在距离像域[8]包含了平移补偿的模板匹配法[9],其匹配度定义为两距离像的所有线性位移之间的最大滑动相关系数。对测试距离像xa,和模板xb,其最大相关系数定义为

p(xa,xb)=maxrxaxb(τ)

(8)

其中rxaxb(τ)为x平移τ后的滑动距离像xa(τ)与模板xb的相关系数。设滑动距离像和模板距离像之间所有循环移动的最小距离为SED(xa,xb),则

SED(xa,xb)=argmin‖xa(τ)-xb‖2

(9)

由于

‖xa(τ)-xb‖2=‖xa(τ)‖2+‖xb‖2-2xa(τ)xb

(10)

因此SED(xa,xb)使得相关系数rxaxb(τ)=2xa(τ)xb达到最大的两幅一维距离像xa、xb识别。

4 程序实现及结果分析

4.1 功能模块仿真实验

4.1.1 对齐移位数据仿真

图3 移位对齐程序设计结构框图

4.1.2 能量归一化数据仿真

设定一个3×3的二维仿真数组a[3][3]={{0,0,1},{5,5,5},{3,4,5}},即三幅一维距离像。其中数组的每一行都代表一幅一维距离像。根据能量归一化的基本原理:

(11)

分别对每一行的一维距离像进行平方求和,并对求得的平方和进行开根号,最后每一行的每个单元除以所求得的平方和开根号,由此得出一幅能量归一化后一维距离像的,利用for语句[10]循环三次,即将三幅距离像全部归一化。其运行的结果如图4。根据归一化的原理对仿真数据进行手动计算,所得出的结果与用C语言计算的结果完全一致,确定能够实现C语言能量归一化模块的功能。

图4 能量归一化仿真程序输出结果

4.2 识别结果及分析

图5为本设计的雷达目标识别原理图,包括雷达目标识别的预处理:对齐移位和能量归一化,分类器的设计等环节。

图5 雷达目标识别系统原理图

实际数据分别是“安-26”、“奖状”、“雅克-42”飞机的一维距离像每种飞机针对其姿态敏感性问题分别分了5～7个阶段数据,每个阶段数据有26000幅一维距离像,其经过FFT后所得一维距离像的像采样点数为256。对于每阶段的26000幅一维距离像真对其姿态敏感问题,取每阶段的一维平均距离像,即每隔100幅取一幅距离像,则在每个阶段平均一幅距离像所占的角度为0.014°,每隔100幅取一幅,相当于训练样本中每两幅距离像间的角度差为0.14°,根据微积分原理,可以认为在该小角度范围内的姿态不敏感。所以对训练样本采用等距抽样的方法,即在每一个阶段每隔100幅取一幅一维距离像,组成了一个有260幅距离像的训练样本。

每类每个阶段的距离像都有26000幅,如果把260幅距离像以外的所有距离像作为测试样本,数据量过大无法计算,所以在这里采取不重复简单随机抽样原则,首先给每类目标距离像编号1～26000号,通过Matlab中的函数Random.m产生1～26000内的服从均匀分布随机数130个(取整),将130个随机数对应序列的距离像作为测试样本。这样取测试样本即减少了计算量,同时由于测试样本的随机性,并不影响最后的识别率统计。三种飞机第一阶段的实验结果如表1所示。

表1 三种飞机识别结果

5 结语

本文提出了一种滑动最大相关系数的一维距离像的目标识别方法,并通过C语言对飞机实际数据进行了工程运算,基本能够满足识别要求。但是由于实际数据比较庞大,运算速度较慢,还需要进一步优化设计。

[1] 胡薇.基于特征空间的3D目标识别方法[D].武汉:华中科技大学,2004:43-50.

[2] H. EI-Shishini, et al. A multistage algorithm for fast classification of patterns[J]. Pattern Recognition Letter,1990,10(4):211-215.

[3] 杜兰,刘宏伟,保铮.利用目标方位信息改善雷达距离像识别性能[J].系统工程与电子技术,2004(8):1040-1043.

[4] Li H J, Yang S H. Using range profiles as features vectors to identify aerospace objects[J]. IEEE Trans,1993,41(3):261-268.

[5] 何晓群.多元统计分析[M].第一版.北京:人民大学出版社,2004.

[6] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001:57-82.

[7] 王智君.粗糙集规则简约的方法在模式识别中的应用[J].微计算机应用,2009,30(5):1-4.

[8] 陈凤,杜兰,保铮.一种优化K近邻准则及在雷达HRRP目标识别中的应用[J].西安电子科技大学学报,2007,34(5):681-686.

[9] 张亮,何松华,庄钊文.雷达目标一维距离象多分辨特征描述和快速匹配法研究[J].电子科学学刊,1998(3):552-557.

[10] 谭浩强.C程序设计[M].第三版.北京:清华大学出版社,2005.

Radar Targets Recognition Based on Range Profile

LI Fei

(Unit 92, No. 92941 Troops of PLA, Huludao 125001)

Based on range profile, the application of pattern recognition technology in radar target recognition is researched, and the strength and time-shift sensitivity of HRRP. The principle of relative alignment and absolute alignment are combined to normalize the energy of amplitude-scale sensitivity. The slide maximum correlation is algorithms are implemented by C Language. The recognition result is analyzed.

radar targets recognition, range profile, time-shift sensitivity, amplitude-scale sensitivity

2014年11月7日,

2014年12月26日

李飞,男,助理工程师,研究方向:信息处理测试。

TN957

10.3969/j.issn1672-9730.2015.05.020