指挥信息系统效能指标体系的构建和约简*
戴利军 杨露菁
(海军工程大学电子工程学院 武汉 430033)
指挥信息系统效能指标体系的构建和约简*
戴利军 杨露菁
(海军工程大学电子工程学院 武汉 430033)
建立适当的作战效能评估指标体系对于评估指挥信息系统的效能非常关键,然而,影响指挥信息系统效能的指标繁多,指标间存在冗余和相关性,直接采用这些指标会增加后续效能评估的时空复杂度。在创建作战效能评估指标体系基础上,采用改进的LLE方法实现评估指标集合的约简化,将复杂的指标体系非线性映射到低维的指标数据中,算法有效地降低了近邻点个数对算法的影响,并很好地学习了高维数据的流形结构。实验结果表明方法有效可行。
C4ISR; 效能评估; 指标体系; 局部线性嵌入
Class Number TP18
1 引言
指挥信息系统是指综合运用以计算机为核心的信息技术,以保障各级指挥机构对所属部队及武器平台实施科学、高效的指挥控制为目的,实现作战信息从获取、传输、处理到利用的自动化,具有指挥、控制、通信、信息处理、情报、侦察和监视功能的军事信息系统[1]。指挥信息系统在现代的信息化战争中的作用和地位非常重要,被称作是信息化战中兵力“倍增器”和作战指挥的“中枢神经”。指挥信息系统的评估工作是系统研究的根本点,对系统的建设工作具有指导性的意义。因此,准确地科学地评估指挥信息系统效能具有非常重要的意义。但是,指挥信息系统是一个庞大而复杂的系统,它具有多种功能,系统的组成结构非常复杂,这也就使得其效能指标非常复杂,指标之间还存在相关性和冗余。这样的情况下,直接使用这些指标进行评估就会使得后续工作的时空复杂度增加许多,评估的效率也会降低。因此,对指挥信息系统复杂的评估指标体系进行约简是指挥信息系统效能评估工作中的关键一步。
流形学习的本质是当采样数据所在的空间为一个低维光滑流形时,要从采样数据学习出低维流形的内在几何结构和规律。所以流形学习比传统的数据降维方法更能体现事物的本质。近年已经提出了多种应用较为广泛的流形学习方法[2~5],比如Isomap、局部线性嵌入(LLE)、拉普拉斯特征映射(Laplacian Eigenmaps)、局部切空间排列(LTSA)以及Discriminative Locality Alignment[6](DLA)等。其中LLE方法的原理是保留数据点的局部性质,利用局部的线性来逼近全局的非线性性,通过重合的部分邻域来获得全局结构的信息,从而保持整体的几何性质。但LLE方法的不足之处在于其默认样本在高维空间内是均匀分布的,而实际上流形上每个样本点的近邻点只是近似地分布在流形的一个局部线性区域内,选取不同的近邻点个数就会造成不同的重构误差,降维的效果也会不同,所以很有必要构造一个近似重构系数来约束重构误差,从而减少近邻点个数的选取对降维效果的影响。所以,采用了一种改进的LLE算法。通过构造样本点重构误差的近似重构系数,改进算法可以有效地降低近邻点选取对算法的影响,并很好地学习高维数据的流形结构,实现指挥信息系统效能评估指标体系的约简,通过非线性映射将复杂的指标体系映射到低维的指标数据中,从而明显减少了数据的维数,保留了重要的指标,去除了冗余的指标。
2 指挥信息系统效能指标体系的建立
由于指挥信息系统的各分系统的复杂性及功能的多样性,要建立一个可以使得效能评估过程有效有序的效能指标体系就变得非常复杂。根据指挥信息系统的工作流程,其系统组成以及效能评估的目的,可以采用层次分析(AHP)法来确定指挥信息系统的效能指标体系。AHP法可以将复杂体系分解为层次结构明显的有序结构[7],在本文中,将指挥信息系统的指标体系粗略地分解为四层,即系统能力、一级子能力、二级子能力以及具体性能指标。一级子能力主要包括信息获取能力、信息传输能力、信息处理能力、辅助决策能力和指挥控制能力。采用层次分析(AHP)法对指挥信息系统进行分解可得到一个包含33个指标的指标体系。如表1所示。
3 系统效能指标体系约简模型
3.1 效能指标数据及处理方法
由于指挥信息系统是一个很复杂的系统,所以其评估指标也较复杂。其中指标可分为定性指标和定量指标,定量指标又可分为效益型指标、成本型指标、固定型指标和区间型指标等不同的形式。在对数据样本进行分类处理之后,数据的格式依然是不统一的,不能支持机器计算。如定量指标具有不同的量纲,而定性指标具有不一样的描述方式。所以要对定性指标进行科学的量化,对不同量纲的指标进行无量纲的标准化处理。

表1 C4ISR的每个样本指标及指标类型

1) 效益型
(1)
2) 成本型
(2)
3.2 改进的LLE方法
在指挥信息系统效能的评估过程中,从众多指标中选出合理的、科学的指标体系,以减少由过多指标引起的不确定性是非常关键的一个步骤。根据指挥信息系统的指标特征,本文采用改进的LLE方法进行属性约简,去除对评估过程影响较小的指标,降低评估过程所建模型的时空复杂度,从而提高系统效能评估的效率。
3.2.1 理论分析
对LLE的实施步骤进行分析可以得出,不同近邻点个数的选取会使降维的结果有很大的不同。为了让近邻点个数的选取对实验结果的影响减少,构造近似重构系数对重构误差进行约束就是一个可行的方法。
聚类的中心包含着大量的信息,所以聚类分类能够尽可能多地保留样本点的原有信息,因此使用聚类分析的方法改进LLE是可行的。文献[9]提出了基于聚类的LLE方法,该文采用K均值聚类算法,以聚类的中心点代表每一类,减少了样本点的个数从而降低了计算量。所以可以利用总体样本的中心以及聚类分类后各类的中心来构造样本的近似重构系数并约束重构误差,减少近邻点个数的选取对LLE算法的影响,从而对原LLE进行改进。
模糊C均值聚类方法(FCM)[10]采用的模糊聚类分析并不像传统的聚类分析一样严格地划分每个待识别的对象,而是运用对象对类的隶属度,对对象进行模糊的划分,而且FCM算法是基于目标函数的模糊聚类算法理论中最完善、应用最为广泛的一种算法,因此本文采用FCM算法。
3.2.2 改进的LLE算法
给定的高维观测数据集为X={x1,x2,…,xN},xi∈RD,采样自d维流形[11],求低维坐标Y={y1,y2,…,yN}。设将样本点聚类分成C个类,第j类样本的中心为mj,第j类样本的个数为n(j)。
那么第j类样本与总体样本中心的距离为
(3)
第j类样本点的类内平均距离为
(4)
m为总体样本的中心。根据式(3)和式(4),定义样本点重构误差的近似重构系数为
(5)
J为样本点i所属的类,(j=1,2,…,C)。
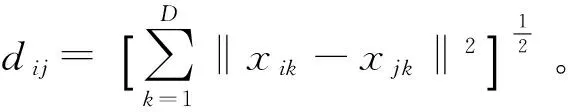
步骤2 求出样本点的局部重建权值,使得重建误差最小,计算局部重建权矩阵{wij}。结合限制条件,即求:

(6)

=2Ziwi+λ×1Ziwi
通常采取简单的求解方法,令Ziwi=1,来求得wi。

(7)
(8)
4 实验
由STAGE(Scenario Toolkit And Generation Environment)仿真系统多次运行获得145组45维的实验样本,作为指标体系约简的数据样本。为了形象地表明降维后的结果,分别选取输出维数d为3和2,将降维结果直观地显示在三维空间和二维平面上,近邻点个数K=9。
采用改进的LLE方法,将145组维度为45的样本数据映射到三维空间和二位平面,结果如图1(a)和图1(b)所示,从图1(a)和图1(b)的对比中可以看出,改进的LLE方法在降维过程中能够很好地保持原有高维数据在空间内的邻接关系,所以改进的LLE方法能够有效地对此类数据进行降维。


图1 降维效果图
5 结语
1) 对指挥信息系统系统效能指标体系进行属性约简,能够为后续的效能评估降低空间和时间的复杂度,提高评估的效率。
2) 新提出的改进的LLE算法,可以明显减少近邻点的选取对降维结果的影响,而且还能较好的保留原始数据的几何结构,降维实验也证明了该方法的可行。
[1] 曹雷,鲍广宇,陈国友,等.指挥信息系统[M].北京:国防工业出版社,2012:15-18.
[2] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science,2000,290(5500):2323-2326.
[3] Tenenbaum J B, de Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science,2000,290(5500):2319-2323.
[4] Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Advances in Neural Information Processing Systems 14. Vancouver: MIT Press,2001:585-591.
[5] Zhang Zhenyue, Zha Hongyuan. Principal manifolds and nonlinear dimensionality reduction via local tangent space alignment[J]. SIAM Journal of Scientific Computing,2004,26(1):313-338.
[6] Zhang Tianhao, Tao Dacheng, Zhao Deli, et al. Patch alignment for dimensionality reduction[J]. IEEE Transactions on Knowledge and Data Engineering,2009,21(9):1299-1313.
[7] 吴小勇.反潜体系的搜索能力优化方案[D].长沙:国防科技大学,2012:42-47.
[8] 郑玉军,张金林,李跃华.基于GA-BP神经网络的某型装备作战效能评估方法[J].空军雷达学院学报,2012,26(5):346-348.
[9] 王和勇,郑杰,姚正安,等.基于聚类和改进距离的LLE方法在数据降维中的应用[J].计算机研究与发展,2006,43(8):1485-1490.
[10] Theodoridis S, Koutroumbas K.模式识别[M].李晶皎,王爱侠,张广渊,译.3版.北京:电子工业出版社,2006:75-77.
[11] 焦李成,公茂果,王爽,等.自然计算、机器学习与图像理解前沿[M].西安:西安电子科技大学出版社,2008:166-171.
Establishment and Reduction of Effectiveness Index System for C4ISR
DAI Lijun YANG Lujing
(College of Electronic, Naval University of Engineering, Wuhan 430033)
Constructing appropriate evaluation index for C4ISR is critical to evaluate its effectiveness, affecting the operational effectiveness of a range of indexes, indexes redundant and direct use of these indexes will increase the time-space complexity of effectiveness assessment, multiple and multi-scale indexes for the system were establish-ed. In order to reduce the complexity of index, improved LLE is taken to project these data into low dimensional data nonlinearly. The proposed algorithm can reduce the influence of the number of neighbors efficiently and the probability of the database is retained. This is confirmed by experiments.
C4ISR, effectiveness evaluation, index system, LLE
2014年11月8日,
2014年12月27日
戴利军,男,硕士研究生,研究方向:作战辅助决策技术。杨露菁,女,教授,博士生导师,研究方向:指挥信息系统建模与分析。
TP18
10.3969/j.issn1672-9730.2015.05.006

