基于传递率函数的运行模态分析方法*

张永年， 王 彤， 夏遵平

(南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)



基于传递率函数的运行模态分析方法*

张永年， 王 彤， 夏遵平

(南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

传统的运行模态分析方法在推导过程中多假设激励为白噪声，造成在应用上有一定的局限性。提出了一种基于传递率函数的运行模态分析方法，无需采用白噪声假设，利用两种不同载荷情况下的传递率函数构造有理函数，通过有理分式Forsythe正交多项式法对其进行拟合，得到模态频率、阻尼和振型参数。最后，采用机翼模型仿真算例和悬臂梁实验，验证了在非白噪声激励情况下该方法的有效性与可靠性。

模态参数识别； 运行模态分析； 传递率函数； 有理函数； 正交多项式

引 言

随着科学技术的发展，在航空航天、车辆、机械、土木等工程领域，结构动力学问题日益突出。模态分析技术已成为解决此类问题不可或缺的手段，其中，传统的实验模态分析方法(experimental modal analysis，简称EMA)是在实验室中完成，实验结果准确，相关的实验方法也较为完善[1]。运行模态分析(operational modal analysis，简称OMA)是只从振动响应信号中提取模态参数的一项技术[2]。这与EMA相比，OMA不需要人工激励，测试成本低且能在系统正常运行情况下进行测试，更能反映系统真实的动力学性能。

近年来发展了许多运行模态识别方法。其中，时域方法占大多数并且应用更为广泛，代表性的有随机减量(random decrement technique，简称RDT)法[3]、基于ARMA模型的时序分析法[4]、自然激励识别技术(natural excitation technique，简称NExT)[5]和随机子空间(stochastic subspace identification，简称SSI)法[6]等。与时域方法相比，在频域方面运行模态识别方法较少。早期主要采用基于响应功率谱密度函数进行模态参数识别的峰值选取法(peak-picking，简称PP)。1999年，Brinker等[7]提出了频域分解(frequency domain decomposition，简称FDD)法，该方法在工程领域应用较多，但对于阻尼的识别精度不高。王彤等[8-9]提出频域空间域分解法，该方法通过增强功率谱得到准确的频率和阻尼。这些方法都基于环境激励为白噪声的假设。在实际的工程应用中，系统所受的环境激励是丰富多样的，并非是理想的白噪声类型。若系统所受的环境激励不是白噪声，采用传统的运行模态分析技术进行测试分析会带来误差，甚至得到错误的结果。基于传递率函数的运行模态分析方法对于环境激励力的性质要求较低，激励力可以是白噪声、脉冲激励和谐波激励等。由于它无需“白噪声激励”这一前提，因此一方面扩大了运行模态分析技术的使用范围，另一方面也提高了运行模态参数识别的可靠度与精度。因此，基于传递率的运行模态分析方法[10]的研究具有较大的工程意义。

笔者采用频响函数的Hv计算来估计传递率函数。利用有理分式正交多项式法[11]拟合构造的有理函数，得到系统的模态频率与阻尼，并通过对传递率函数矩阵奇异值分解得到结构的振型。通过机翼模型仿真算例和悬臂梁实验检验了该算法在非白噪声激励下的有效性和可靠性。

1 理论背景

与频响函数的定义类似(运动响应/激励力)，传递率函数的定义为(运动响应/运动输入)。在拉普拉斯域中，输出自由度i与参考自由度j的传递率函数Tij定义为

Tij(s)=Xi(s)/Xj(s)

(1)

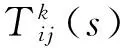
φir/φjr

(2)

其中：φir和φjr为系统第i和j自由度的第r阶振型。

φir/φjr

(3)

由式(2)和式(3)可得

(4)

(5)

其倒数为

(6)

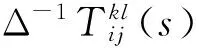
(7)

其中：p，q分别为分子分母多项式的阶数；ak和bk为多项式分子分母多项式系数向量。

为减少方程求解过程中的病态性并解耦系统矩阵，采用Forsythe正交多项式有理分式形式

(8)

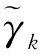
通过最小二乘拟合获得系统的模态频率与阻尼。

系统振型可通过对构造的传递率函数矩阵在系统模态频率处奇异值分解得到[12]。

(9)

对式(9)奇异值分解取奇异值向量第一列，即得到结构的振型。

2 仿真算例

弯扭二自由度机翼模型被广泛应用于飞机飞行颤振分析的仿真。该模型仿真真实机翼的截面，模型平动和转动可仿真真实飞机机翼的弯曲和扭转模态。机翼物理模型和简化的力学模型如图1,2所示。

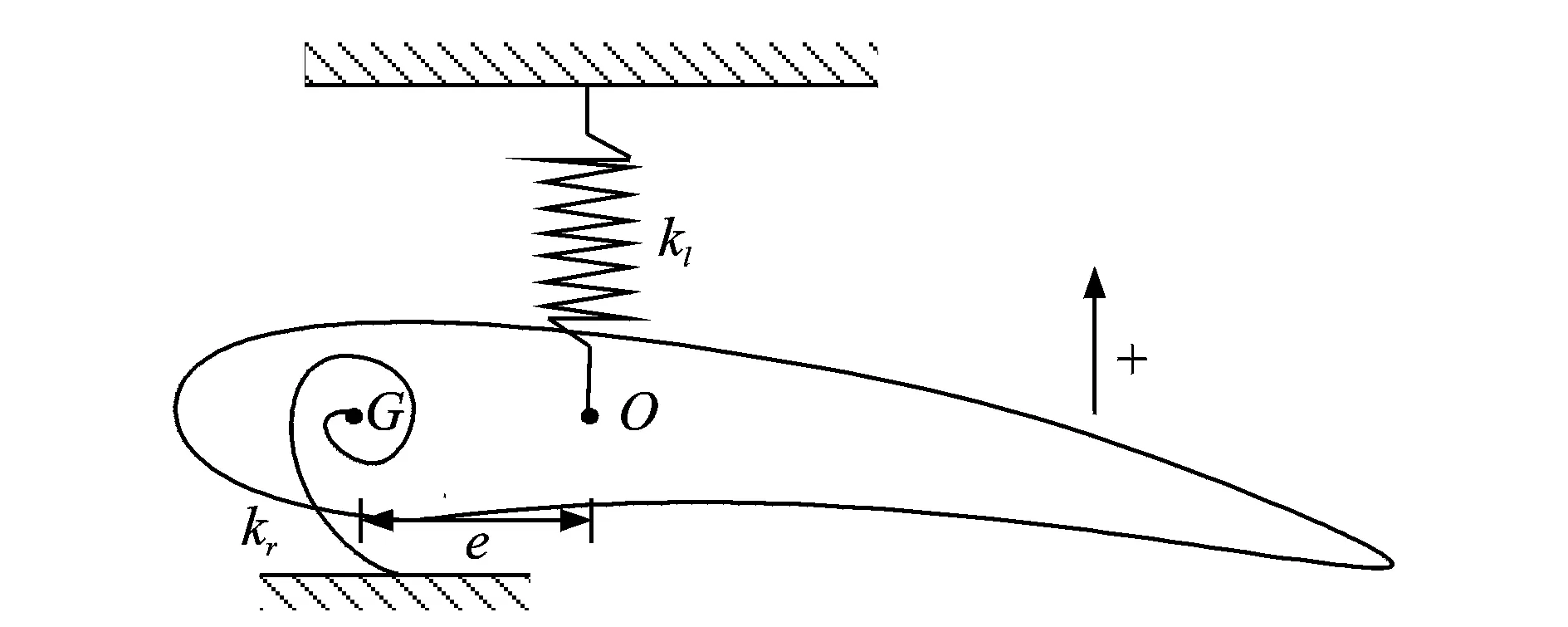
图1 机翼物理模型Fig.1 The physical model of the wing

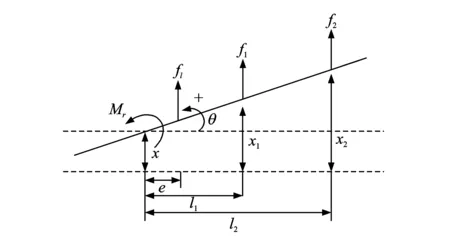
图2 机翼力学模型Fig.2 The mechanical model of the wing

机翼模型物理参数设置如表1所示，对模型添加比例阻尼C=0.000 4K。

表1 机翼的物理参数

为验证该算法对非白噪声激励情况下模态参数的识别效果,激励信号分别采用两种典型的非白噪声信号仿真得到响应信号：情况1，粉红噪声(Pink noise)；情况2，间歇脉冲激励。通过改变激励点，得到两种载荷情况下的加速度响应数据。

仿真采样频率为64 Hz，数据长度为6 400点。仿真得到两种信号激励情况下的响应信号分别如图3和图4所示。对应的激励信号自功率谱(power spectrum density，简称PSD)如图5和图6所示，为非白噪声信号。

选取2号点为参考点，根据两种载荷下的加速度响应数据构造有理函数，情况1和情况2下有理函数及其拟合如图7和图8所示。

图3 模型的仿真时间响应(情况1)

图4 模型的仿真时间响应(情况2)

图5 激励信号功率谱(情况1)

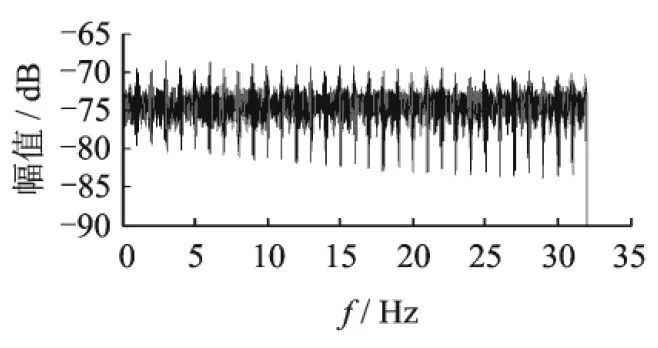
图6 激励信号功率谱(情况2)

图7 有理函数及其拟合(情况1)

图8 有理函数及其拟合(情况2)

图9和图10为采用响应谱和传递率函数矩阵奇异值分解得到的模态指示曲线。该仿真算例中数据长度为6 400点，由于激励信号非白噪声，且采集得到的响应信号数据量较少，采用传统方法得到的模态指示曲线毛刺较多，不够清晰。

识别得到情况1和情况2下机翼的模态参数与其理论值对比如表2和表3所示。

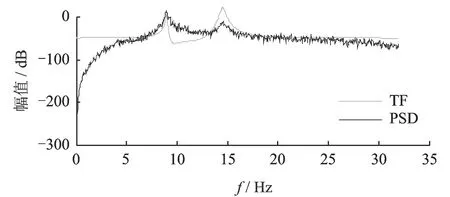
图9 模态指示曲线(情况1)Fig.9 The curve of mode indicator (case 1)

图10 模态指示曲线(情况2)Fig.10 The curve of mode indicator (case 2)

理论频率/Hz识别频率/Hz频率误差/%理论阻尼/%识别阻尼/%阻尼误差/%8.978.970.001.131.12-0.8814.5214.51-0.071.821.830.55

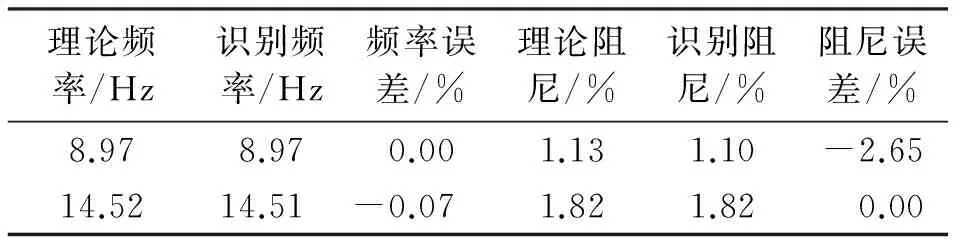
表3 结构模态参数及误差分析(情况2)

由上表可看出，该算法对非白噪声激励情况下也适用，且具有较高的识别精度。另外该算法与传统的方法相比所需数据量少，提高了识别效率。经测试，在Inter(R) Core(TM) i3-2310M处理器下，参数识别耗时0.69 s，识别速度较快。

3 实 验

采用基于传递率函数的运行模态分析方法对悬臂梁进行模态参数识别。实验装置如图11所示，在一根铁质的悬臂梁上等间距布置4个ICP加速度传感器，激励采用螺丝钉人工连续敲击(激励为脉冲激励)，并且采用分别敲击1号和3号点得到两组不同载荷情况下的响应信号。

采样频率为1 280 Hz，采样时间设置为12.8 s，采样点数为16 384点。首先敲击1号点，采集得到第一种载荷情况下的输出信号，该激励情况下2号点的输出信号，如图12所示。然后再敲击3号点，采集得到第二种载荷情况下的输出信号。

因为梁的自由端4号点振幅较大，相对信噪比较高，故选取该点作为参考点。选取3号点分析，构造得到基于传递率函数的有理函数。采用有理分式正交多项式法对构造得到的有理多项式函数进行拟合，拟合结果如图13所示。

为验证该算法识别结果的精度，作为对比，采用力锤激励对悬臂梁做EMA实验。由于采用力锤激励，人工激励输入可测，且测试信噪比高，识别结果精确可靠，故可视EMA识别结果为结构真实参数。基于传递率函数(transmissibility functions，简称TF)法和频域空间域分解(frequency spatial domain decomposition，简称FSDD)法识别结果与EMA频率和阻尼参数识别结果对比如表4和表5所示。

图11 实验装置图

图12 2号点的响应

图13 有理函数拟合

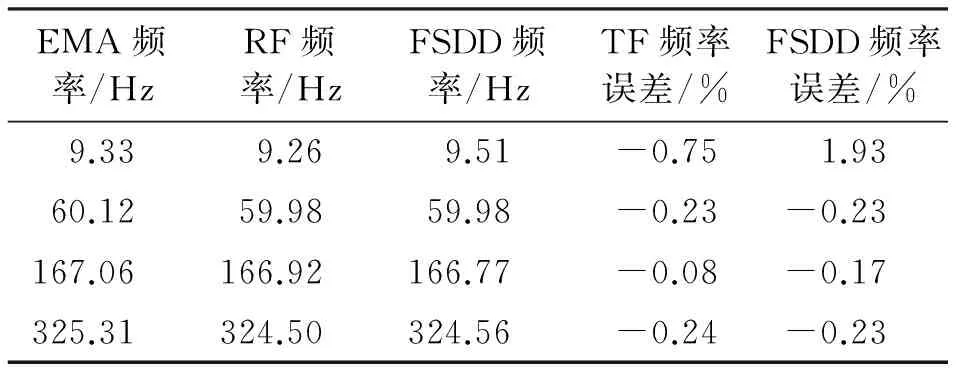
表4 频率参数及误差分析

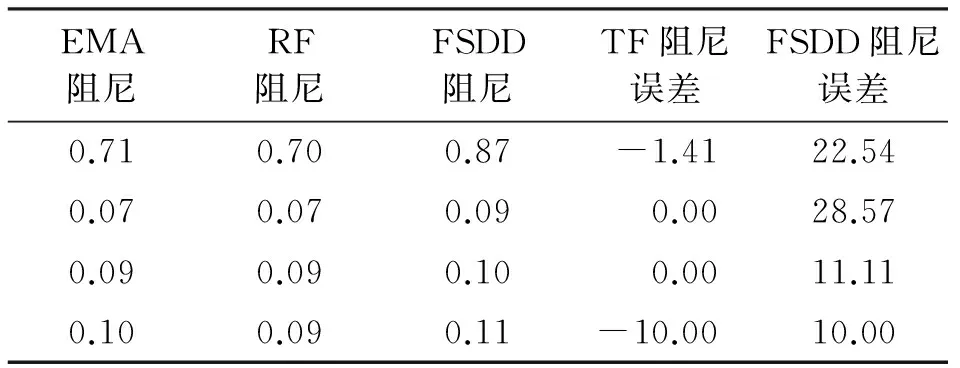
表5 阻尼参数及误差分析

由表4，5可看出，基于传递率函数法识别得到的频率和阻尼参数与EMA识别得到的结果相对误差较小，频率误差1%以内，阻尼误差10%以内，识别结果可靠。该算法识别得参数共耗时0.739 s，具有较高的识别效率。

在非白噪声和短数据情况下，采用基于传递率函数法仍能得到较为理想的有理函数，能清晰的指示出模态频率。另外，两种方法得到的模态指示曲线如图14所示，可以看到功率谱法得到的模态指示曲线毛刺较多，模态指示不清晰。

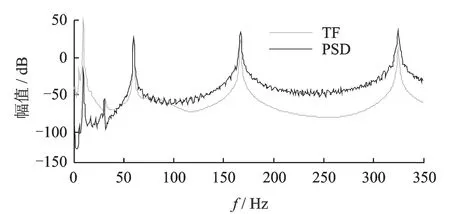
图14 模态指示曲线Fig.14 The curve of mode indicator

因此基于传递率函数的运行模态识别方法在非白噪声激励和短数据情况下具有一定的优越性。该算法识别得到悬臂梁的振型如图15所示。

图15 悬臂梁的4阶模态振型Fig.15 Four mode shapes of simply cantilever beam

4 结 论

1) 该方法需要至少二种不同载荷情况下的响应信号来识别模态参数。在实际工程应用中，由于环境激励的随机性，两种不同载荷情况下的数据理论上可通过不同时间段采集的数据得到。

2) 仿真和实验表明，该方法即使在非白噪声信号激励和短数据情况下也能得到较为理想的识别结果。因此，该方法有望拓展OMA的应用范围。

3) 适当提高拟合阶次能得到更好的识别结果，与此同时带来的计算模态可通过判断阻尼大小、查看有理函数拟合图以及振型动画等方法予以剔除。

[1] 王彤, 张令弥.多频段拟合的正交多项式方法及其Matlab工具箱[J].振动工程学报,2004,25(6):560-564.

Wang Tong, Zhang Lingmi. A multiple frequency band fitting method using orthogonal polynomials and corresponding Matlab toolbox[J]. Journal of Vibration Engineering, 2004,25(6):560-564. (in Chinese)

[2] 张义民,张守元,李鹤,等.运行模态分析中谐波模态识别方法研究及应用[J].振动、测试与诊断,2008,28(3):197-200.

Zhang Yimin, Zhang Shouyuan, Li He, et al. Harmonic mode identification in the operational modal analysis and its application[J]. Journal of Vibration, Measurement & Diagnosis, 2008,28(3):197-200. (in Chinese)

[3] Ibrahim S R. Random decrement technique for modal identification of structures[J]. AIAA Journal of Spacecraft and Rockets, 1977,14(11):696-700.

[4] Bonnecase D, Provosto M. Application of a multidimensional ARMA model to modal analysis under natural excitation[C]∥Proceeding of the 8th International Modal Analysis Conference (IMAC). Kissemee, Florida, USA: Society for Experimental Mechanics, 1990:382-388.

[5] James G H, Carne T G, Lauffer J P. The natural excitation technique (NExT) for modal parameter extraction from operating structures[J]. Journal of Analytical and Experimental Modal Analysis, 1995,10(4):260-277.

[6] Overschee P V, Moor B D. Identification for linear systems: theory, implementation, application[M]. UK: Kluwer Academic Publishers, 1996:57-89.

[7] Brincker R, Zhang L M, Anderson P. Modal identification from ambient response using frequency domain decomposition[C]∥Proceeding of the 18th International Modal Analysis Conference (IMAC). San Antonio, USA: Society for Experimental Mechanics, 2000:628-630.

[8] Wang Tong, Zhang Lingmi, Tamura Yukio. An operational modal analysis method in frequency and spatial domain[J]. Earthquake Engineering and Engineering Vibration, 2005,4(2):295-300.

[9] 王彤,张令弥.运行模态分析的频域空间域分解法及其应用[J].航空学报,2006,27(1):62-66.

Wang Tong, Zhang Lingmi. Frequency and spatial domain decomposition for operational modal analysis and its application[J]. Acta Aeronautica et Astronautica Sinica, 2006,27(1):62-66. (in Chinese)

[10]Devriendt C, Guillaume P. The use of transmissibility measurements in output-only modal analysis[J]. Mechanical Systems and Signal Processing, 2007,21(7):2689-2696.

[11]王彤,张令弥.有理分式正交多项式频响函数模态参数识别[J].航空学报,2003,24(2):140-143.

Wang Tong, Zhang Lingmi. Modal identification with frequency response function based on rational fraction orthogonal polynomials[J]. Acta Aeronautica et Astronautica Sinica, 2003,24(2):140-143. (in Chinese)

[12]Araujo I G, Laier J E. Operational modal analysis using SVD of power spectral density transmissibility matrices[J]. Mechanical Systems and Signal Processing, 2014,46(1):129-145.

10.16450/j.cnki.issn.1004-6801.2015.05.023

*南京航空航天大学机械结构力学及控制国家重点实验室自主研究课题资助项目(0113G01)；江苏高校优势学科建设工程资助项目

2014-05-27；

2014-09-01

O329； TB123

张永年，男，1990年9月生，硕士。主要研究方向为振动测试与模态参数识别。 E-mail：zyn@dytac.com.cn