车辆垂向轮轨力识别方法与试验*

朱 涛， 肖守讷， 阳光武， 胡光忠

(1．西南交通大学牵引动力国家重点实验室 成都，610031) (2．四川理工学院机械工程学院 自贡，643000)



车辆垂向轮轨力识别方法与试验*

朱 涛1， 肖守讷1， 阳光武1， 胡光忠2

(1．西南交通大学牵引动力国家重点实验室 成都，610031) (2．四川理工学院机械工程学院 自贡，643000)

为了解决轨道车辆轮轨接触载荷难以直接测量的问题，提出了一种轮轨接触力时域识别方法。建立了考虑浮沉和点头的10自由度车辆垂向振动模型，利用车辆系统的加速度响应和位移响应实现了对车辆垂向轮轨接触力的识别；反演模型同时能够实现已测量响应的再现以及对其他非测量部位响应的识别。利用滚动振动试验台测试数据对反演模型进行了验证，研究结果表明：反演模型能够较为准确地对车辆垂向轮轨力进行识别，同时在预测车辆系统非测量部位响应以及测量部位响应再现方面也具有较高的精度，相关系数均大于0.9，为极强相关。

载荷识别； 轨道车辆； 轮轨垂向力； 试验验证

引 言

随着列车运行速度的提高以及曲线半径的减小，车辆轮轨作用载荷急剧恶化，而这些载荷对行车安全性又有着极大的影响[1]。一方面，可以通过改善线路条件或降低车辆运行速度降低轮轨作用力；另一方面，通过对列车轮轨作用力进行测量，进而对列车运行速度与线路之间的匹配合理性以及运行安全性进行评估。一些学者将研究的焦点集中在轮轨接触点的冲击监测上[2-3]，在一定长度的轨道上贴一系列的应变片，对列车运行过程中轨道的应变进行测量，进而计算轮轨作用力。这种方法的显著缺点是必须在轨道上贴非常多的应变片以满足测量要求[4-5]，该方法成本昂贵且困难。另外，用测力轮对连续测定轨道不平顺引起的轮轨相互作用力，便可帮助了解轨道不平顺对轮轨力和脱轨系数、减载率等安全性指标的影响，评定轨道不平顺导致车辆脱轨的可能性。由于轮轨作用力同振动加速度一样，也受行车速度和车辆传递函数的影响，并且测力轮对的价格较高，使用寿命较短，安装不方便，因此国内外只有少数轨检车装备测力轮对设备仅在情况比较复杂、需要对轨道不平顺的影响直接确认时使用。但是，对于轮轨力的获取而言，由于轮轨接触位置是不可及且接触力是不断移动着的，因此无法利用传统的测量方法和传感器对系统动载荷进行直接测量。利用载荷反演技术，通过安装在适当位置的加速度计，对加速度进行测量，用校正和修改后的加速度对轮轨力进行反演识别，恰好可以弥补轮轨力直接测量的不足。

在载荷识别理论方法研究方面，朱广荣等[6]提出了一种基于Wilson-θ算法的动载荷识别方法，为动载荷的时域识别提供了一种新的思路。Ward等[7]提出了一种基于Kalman-Brucy滤波法的车辆线性数学模型和非线性轮轨力接触模型，用于对车辆轮轨接触力的预测。Nordstrom等[8]用一个20自由度二维车辆线性有限元模型对三种较为常用的时域载荷识别方法进行了比较，为载荷识别方法在轨道车辆上的运用提供了一种选择途径。Xia等[9-10]提出了一种基于测量的车体加速度的铁道货车反演模型，对一定速度下的轮轨力进行识别，并利用实验室实验和Virmper动力学软件相结合的方法对反演数学模型进行了验证。朱涛等[11-12]对载荷识别的研究进展以及在铁道车辆上的运用进行了总结，对载荷识别未来的发展方向、在铁道车辆上的运用以及一些有待解决的关键技术提出了其观点，同时提出了一种新的载荷识别方法。

笔者提出了一种非迭代的载荷识别时域方法，建立了考虑浮沉和点头的10自由度车辆垂向振动模型，利用车辆结构的加速度响应和位移响应，实现了对车辆垂向接触力的识别；反演模型同时能够对其他非测量部位的加速度响应进行识别。利用滚动振动试验台测试数据对反演模型进行了验证。

1 数学模型

以一个n自由度定常系统为研究对象，其状态空间方程表达式为

(1)

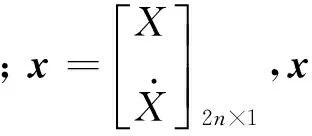
为了便于计算机求解，将系统的连续时间微分方程(1)转化为离散方程，如式(2)，(3)所示

其中：C=eAh，D=A-1(C-I)B分别为关于矩阵A和时间步长h的指数矩阵以及与载荷相关的输入影响矩阵(I为与矩阵C行列式相同的单位矩阵)；Qm×2n为与系统测量数据的测量位置、选择位移还是速度作为测量值、以及待识别载荷的数目有关的输出影响矩阵(n为系统自由度，m为载荷数目)；i+1表示系统在时间为(i+1)h位置的计算。

(4)

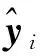
由于大多数情况下，测量值存在一定的误差和噪声，即病态问题，因此在目标函数中增加一个正则化项，此时式(4)变为

(5)

式(5)中增加的项(fi)Tλ2(fi)，即为Tikhonov正则化项，在载荷识别过程中具有决定性的作用。

将动态规划方法以及Bellman最优化原理[12]运用到目标函数的最小化当中，从而在识别出输入载荷的同时，使式(5)中的最小二次方差E最小。在任意初始状态x以及第n个时间步下，有

(6)

利用Bellman最优化原理，推导出式(6)的回归公式

(fn-1)Tλ2(fn-1)+Fn(Cxn-1+Dfn-1)]

(7)

由此得到了经典的动态规划结构表达式，通过对fn-1的计算，使得方程中的前两项在任意点都有最小值。从n=N开始逆向求解至n=1，从而得到最终的解。在端点n=N处，有

(fN)Tλ2(fN)]

(8)

假设fN=0，得到在端点N处的最小值

(9)

由式(9)可以看出，FN是关于xN的二次函数，进而可以证明在n=1～N上，所有的Fn均为xn的二次函数，因此对任意n有

Fn(x)=(xn,Rnxn)+(xn,Sn)+qn

(10)

将式(10)代入式(7)中，得

(xn-1,Rn-1xn-1)+(xn-1,Sn-1)+qn-1=

(fn-1)Tλ2(fn-1)+(Cxn-1+Dfn-1,

Rn(Cxn-1+Dfn-1))+(Cxn-1+Dfn-1,Sn)+qn]

(11)

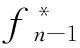
(12)

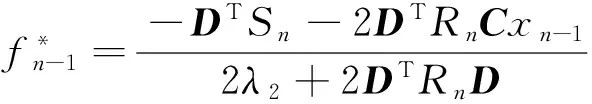
皮尔逊积矩相关系数被广泛应用来度量两个变量线性相关性的强弱，通常用γ或ρ表示，是用来度量两个变量X和Y之间的相互关系(线性相关)的，取值范围在[-1,+1]之间。其表达式为

(13)

利用Matlab软件进行编程计算。

2 车辆垂向轮轨力的识别

2.1 车辆垂向动力学模型的建立

研究表明[13]，车辆的垂向运动和横向运动之间仅存在很弱的耦合作用，因此在研究车辆垂向响应时可以不必包括横向自由度。笔者对垂向响应的研究，只考虑了各构件的浮沉、点头及侧滚共10个自由度，使得研究对象总的自由度数目大大减小，既减少了计算费用又使对计算结果的解释也变得简单。

客车上广泛应用具有两系弹簧装置的两轴转向架，计算四轴客车垂向振动的力学模型如图1所示。

●表示加速度传感器的安装位置；■表示位移传感器的安装位置。图1 车辆垂向动力学模型Fig.1 Vertical dynamic model of the vehicle

基于D′Alembert原理，建立4轴客车的10自由度垂向动力学微分方程[14]，整理得到用于载荷识别分析的质量矩阵、阻尼矩阵、刚度矩阵以及垂向轮轨力矩阵

M=diag([Mc,Jc,Mt,Jt,Mt,Jt,Mw,Mw,Mw,Mw])

F=[0,0,0,0,0,0,Fw1,Fw2,Fw3,Fw4]T

车辆动力学模型中的参数说明：Mc为车体质量；Jc为车体绕Y轴转动惯量；βc为车体绕Y轴转动角度；Mt为构架质量；Jt为车体绕Y轴转动惯量；βt为车体绕Y轴转动角度；Mw为轮对质量；Ksz为转向架一侧二系悬挂垂向刚度；Csz为转向架一侧二系悬挂垂向阻尼；Kpx为每轴箱一系悬挂纵向刚度；Cpz为每轴箱一系悬挂垂向阻尼；lc为车辆定距之半；lt为车辆固定轴距之半；x为纵向位移；y为横向位移；z为垂向位移；Fw为轮对的垂向轮轨力。

根据连续状态方程离散化原理，将连续时间微分方程转化为离散方程，最终得到每个时间点上轮对垂向力f与响应x之间的关系，如式(10)。提出的载荷识别方法利用测得的车辆系统响应对垂向轮轨力进行识别。图2为轮轨垂向载荷识别的步骤。

图2 轮轨载荷反演的步骤Fig.2 Wheel-rail force identification steps

2.2 基于滚动振动试验台的轮轨垂向力识别

利用西南交通大学牵引动力实验室的滚动振动试验台对反演模型进行验证。由24通道的DDS32数采集系统分别对车体垂向加速度、构架的垂向加速度以及4个轴箱垂向加速度和位移等进行采集。试验速度为280 km/h， 输入的激励为武-广线实测轨道谱。基于载荷识别方法， 利用一组测得的垂向加速度响应和垂向位移响应对车辆轮轨垂向力进行

识别，同时对测量部位和非测量部位的加速度响应进行再现和识别，并与测试结果进行对比。

将车体、两个构架的垂向加速度以及第1个轴箱(从左向右计数)的垂向位移作为反演模型的输入，对第3个轮对的垂向轮轨力以及第4个轴箱的加速度响应进行识别，识别结果如图3～6所示。图3为车体的测量加速度与反演加速度的比较(构架和第1个轴箱有类似的结论，在此不再进行比较)，图4为第4个轴箱的测量加速度与反演加速度的比较。图5为第3个轮对垂向轮轨力测量结果与反演结果的比较。图6为图5在0.50～0.65 s之间的放大图。

图3 车体的测量加速度与反演加速度比较Fig.3 Measured and inversed accelerations comparison for the carbody

图4 第4个轴箱测量加速度与反演加速度比较Fig.4 Measured and inversed accelerations comparison for the fourth axle box

图5 第3个轮对垂向轮轨力的反演结果Fig.5 The estimated vertical dynamic contact force for the third wheel-set

图6 第3个轮对垂向轮轨力放大图Fig.6 The enlarged view for estimated vertical dynamic contact force of the third wheel-set

从图3可以看出，利用反演模型实现了对车体垂向加速度的再现，且该结果与滚动振动台测量结果非常吻合，利用式(13)计算其相关系数为0.981 4，为极强相关。从图4对第4个轴箱加速度的反演结果可以看出，在整个时间历程上反演结果与试验测量结果非常接近，说明反演模型在对车辆非测量部位输出响应的识别上具有较高的精度，其相关系数达到0.975 6，也为极强相关。图5～6为反演出的第3个轮对的垂向轮轨力识别结果与试验结果的比较，从垂向轮轨力局部放大图可以看出，虽然有个别时刻力峰值的反演结果与测量结果不太吻合，但在整个时间历程上二者吻合较好，趋势基本一致，其相关系数为0.921 5，为极强相关。需要说明的是，反演方法识别出的轮轨垂向接触力是轨道随机不平顺引起的轮轨动态作用力，由于加速度传感器在低频范围的限制，轮轨垂向力的实际结果是由反演出的动态作用力与车辆重力的反作用力之和构成的。

3 结 论

1) 车辆在滚动振动台上试验速度为280 km/h下，车辆垂向轮轨力识别结果与试验测量结果在时域上具有较高的吻合度，二者在某些时刻的峰值也很接近，其相关系数达到0.921 5，属于极强相关。

2) 基于反演模型不仅可以实现轮轨垂向力的识别，同时也实现了利用一组测得的垂向加速度响应和垂向位移响应对车辆其他非测量部位加速度响应的识别。试验结果与识别结果的比较表明在时域内二者吻合度很高，相关系数也均在0.9以上，属于极强相关。

3) 由于试验条件的限制，笔者仅利用反演模型进行了车辆垂向轮轨力的识别及其试验验证。从评估车辆运营安全性的角度讲，轮轨横向力也是非常重要的，需要在今后的研究中对轮轨横向力的识别进行试验验证。

[1] 翟婉明. 车辆-轨道耦合动力学[M]. 北京:中国铁道出版社, 2001:288-292.

[2] Lechowicz S, Hunt C. Monitoring and managing wheel condition and loading[C]∥Proceeding of International Symposium for Transportation Recorders. Virginia: National Transportation Safety Board, 1999: 205-239.

[3] Nielsen J C O, Johansson A. Out of round railway wheels-literature survey [J]. Journal of Rail and Rapid Transit(Proceedings of the Institute of Mechanical Engineers-part F),2002, 214:79-91.

[4] Chudzikiewicz A. Selected elements of the contact problems necessary for investigating the rail vehicle system[C]∥Advanced Railway Vehicle System Dynamics. Warszawa: Wireless Network Technology, 1991:89-100.

[5] Chudzikiewicz A. Elements of vehicle diagnostics[M]. Radom:Institute of Traffic Engineers, 2002:207-220.

[6] 朱广荣, 陈国平, 张方, 等. 基于Wilson-θ算法的动载荷识别及影响因素[J]. 振动、测试与诊断， 2012, 32(5):709-713.

Zhu Guangrong, Chen Guoping, Zhang Fang, et al. Dynamic load identification based on Wilson-θ method and influence factors[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5):709-713. (in Chinese)

[7] Ward C P, Goodall R M, Dixon R. et al. Adhesion estimation at the wheel-rail interface using advanced monitoring at the wheel-rail interface[J]. Vehicle System Dynamics, 2012, 50(12):1797-1816.

[8] Nordström L, Nordberg T P. A critical comparison of time domain load identification methods[J]. The Japan Society of Mechanical Engineers, 2002, 2: 1151-1156.

[9] Xia F, Bleakley S, Wolfs P. The estimation of wheel rail interaction forces from wagon accelerations[C]∥Advances in Applied Mechanics. Melbourne: Institute of Materials Engineering Australasia, 2005:333-338.

[10]Xia F J, Cole C, Wolfs P. An inverse railway wagon model and its applications[J]. Vehicle System Dynamics, 2007, 45(6): 583-605.

[11]朱涛, 肖守讷, 阳光武. 载荷识别研究进展及其运用于铁道轮-轨载荷研究概述[J]. 铁道学报， 2011, 33(10):30-36.

Zhu Tao, Xiao Shoune, Yang Guangwu. State-of-the-art development of load identification and its application in study on wheel-rail forces[J]. Journal of the China Railway Society, 2011, 33(10):30-36. (in Chinese)

[12]Garg V K, DukkiPati R V. Dynamics of railway vehiele systems[M]. Canada:Academic Press, 1984:169-180.

[13]王福天. 车辆系统动力学[M]. 北京:中国铁道出版社,1981:102-104.

10.16450/j.cnki.issn.1004-6801.2015.05.014

*国家自然科学基金资助项目(51275432,51505390)；四川省科技厅应用基础研究项目(2014JY0242)；牵引动力国家重点实验室自主研究课题(2012TPL_T03、2014TPL_T04)

2013-10-18；

2013-11-10

TB533

朱涛，男，1984年2月生，博士、助理研究员。主要研究方向为轨道机车车辆碰撞动力学和轮轨力识别等。曾发表《Force identification in time domain based on dynamic programming》(《Applied Mathematics and Computation》2014，No.235)等论文。 E-mail:zhutao034@swjtu.cn