路面功率谱密度换算及不平度建模理论研究*

杜 峰， 葛晓成， 陈 翔， 丁金全

(1.华南理工大学机械与汽车工程学院 广州，510641) (2.重庆大学机械传动国家重点实验室 重庆，400030) (3.吉林大学汽车仿真与控制国家重点实验室 长春，130022)



路面功率谱密度换算及不平度建模理论研究*

杜 峰1， 葛晓成2， 陈 翔3， 丁金全3

(1.华南理工大学机械与汽车工程学院 广州，510641) (2.重庆大学机械传动国家重点实验室 重庆，400030) (3.吉林大学汽车仿真与控制国家重点实验室 长春，130022)

为了明晰路面不平度空间域统计量的计算，以及几种重要功率谱密度(power spectral density,简称PSD)之间的关系，以帕塞瓦尔定理和维纳-辛钦定理为依据，在推导空间域自相关函数和PSD计算公式的基础上，导出了不平度空间域位移、速度与加速度PSD以及空间频率与角频率PSD之间的换算关系。另外，为了完善傅里叶逆变换法路面建模中PSD离散化的理论基础，以傅里叶级数与变换、离散傅里叶变换和频域卷积定理为依据，从离散化的原因、目的和结果验证出发论证了PSD离散化的正确性。就模拟路面验证问题，指出直接法谱估计的不合理之处，论证了平均周期图法谱估计时，空间与时间采样频率分别对应着空间域和时间域PSD输出。结果表明，上述换算关系和论证是正确的，可应用于路面不平度建模和汽车平顺性分析。

公路； 汽车平顺性； 功率谱密度； 路面不平度建模

引 言

空间域随机信号分析对于路面不平度建模和汽车平顺性分析非常重要[1-3]，大多文献通过车速将其转换到时间域进行分析，影响了对路面空间域统计量的计算和理解。

空间域路面不平度位移、速度和加速度功率谱密度之间的换算关系，是汽车平顺性分析的重要基础。文献[4]已给出确切表达式，但没有解释原由。文献[5]也没给出推导，现有文献大多直接应用其结论[6]。卢士富[7]研究了这个问题，现在加以推导。

路面不平度空间频率功率谱密度Gq(n)和空间角频率功率谱密度Gq(Ω)之间的数量关系，在运用维纳-辛钦定理，经由功率谱密度计算随机信号的标准差时非常重要，模拟路面标准差是验证生成路面准确性的基本依据之一，但对此关系的分析论证和检验很少，散布在文献中的应用显示对二者关系理解不够全面，需要做深入研究。

针对上述现象，笔者将以帕塞瓦尔定理和维纳-辛钦定理为理论依据，对路面空间域自相关函数和功率谱密度的计算做出分析，并推导出路面不平度位移、速度和加速度功率谱密度之间换算关系，根据傅里叶变换对的两种形式和文献[4-5]，论证了空间频率和角频率功率谱密度之间的两种对应关系。

在汽车平顺性仿真中，基于功率谱密度离散化的傅里叶逆变换法是路面空间建模的常用方法之一，其建模思想比较成熟，但尚有一个关键步骤缺乏严格理论分析[8]——功率谱密度离散化。现有文献通常都略过这些问题[9]。

另外，在应用傅里叶逆变换法做路面模拟时，细节处理不当会导致错误。奇偶采样点的对称设置有区别，功率谱密度验证不能采用直接法计算，平均周期图法谱估计采用空间和时间采样频率分别对应着不同的功率谱密度输出，这类关键细节在之前文献很少涉及，文中将逐一分析。

笔者在深入理解傅里叶变换不同分类(周期连续信号傅里叶级数和傅里叶变换、能量信号傅里叶变换、离散时间傅里叶变换、离散傅里叶变换和周期离散信号傅里叶级数)本质特性的基础上，综合运用傅里叶变换思想和频域卷积定理，从理论上严格分析了功率谱密度离散化的问题，并对工程应用中的几个关键细节给予分析，完善了基于功率谱密度离散化的傅里叶逆变换法路面建模的理论基础，为准确模拟路面不平度，进行汽车平顺性分析提供了保障。

1 空间域路面不平度计算

频率可以指空间、时间和其它虚拟域，是单位域长度所包含波长的个数。路面建模在空间域中研究路面形状，故采用空间频率n，指单位空间(1 m)中所包含的路面波形的波长个数。空间角频率Ω=2πn。空间频率和角频率分别对应时间域中的f和2πf，空间域信号变量l对应时间域变量t。

1.1 位移不平度自相关函数和功率谱密度

路面位移不平度q=q(l)，其中自变量是长度，因变量是高度，均为长度单位量纲。q(l)为时域无限信号，工程中通常截取一段长度L进行研究。L的取值，要保障空间频率分辨率，对于路面不平度信号的空间频率在[0.011 2.83]m-1之间，故最小辨识频率dn=1/L≤0.011，即L≥91 m。

空间长度L的路面不平度信号为

(1)

其自相关函数为

(2)

其中：qL(l)为空间域有限信号，其空间域频谱为连续谱Q(n,L)。

根据帕塞瓦尔定理，路面不平度信号的平均功率为

(3)

空间域单边功率谱密度Gq(n)为

(4)

由维纳-辛钦定理可换算出路面位移不平度时间域功率谱密度Gq(f)。

(5)

其中：l=ut(位移等于车速与时间乘积)，f=nu(时间频率等于空间频率与车速乘积)。

1.2 位移和速度及加速度功率谱密度关系

由自相关定义式(2)可得

(6)

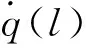
自相关函数对长度变量l的一、二阶导数[7]分别为

(7)

(8)

根据维纳-辛钦定理，改变求导和积分次序得

(9)

(10)

由式(8～10)可得

(11)

同理将自相关函数求三、四阶导数，可得

(12)

1.3 空间频率和空间角频率功率谱密度关系

首先将傅里叶变换的常用形式表述如下

(13)

GB/T 7031—2005和ISO 8608—1995中的一个重要关系式(14)可以作为空间频率功率谱密度Gq(n)与角频率功率谱密度Gq(Ω)关系论证的依据。

Gq(n0)=16Gq(Ω0)

(14)

统计分析表明，路面随机高程信号满足零均值高斯分布，即q～N(0,σ2)，其均方值与零位置自相关函数值相等。

(15)

根据维纳-辛钦定理，由式(13)可知零位置自相关函数值为

(16)

由式(15，16)可知

Sq(Ω)=Sq(n)

(17)

根据式(14)做一验证，虽然Ω=2πn，但不包括Ω0和n0点，其值[4-5]分别为1 rad/m和0.1 m-1。

(18)

(19)

由式(17～19)可得，Gq(n0)=2.533Gq(Ω0)，与式(14)不同。注意到傅里叶变换对的另一种表达，如式(20)所示，则自相关函数如式(21)所示。

(20)

(21)

由式(15)，(21)得到Gq(Ω)dΩ=Gq(n)dn，故

Sq(n)=2πSq(Ω)

(22)

将式(18)，(19)代入式(22)，得Gq(n0)=16Gq(Ω0)，与国标一致，说明在国标和ISO文件中，由采样路面信号自相关函数求路面位移功率谱密度时，采用的傅里叶变换为式(20)，而不是通常采用的式(13)，同时也验证了关系式(22)的正确性。

综合上述分析，空间频率和角频率功率谱密度的关系，随着维纳-辛钦定理使用时所采用的傅里叶变换对的形式而不同，即关系式(17)对应式(13)，关系式(22)对应式(20)。

关系式(17)对应式(13)的正确性检验将在1.4.1节，对应用这个数量关系计算的路面不平度位移标准差作校验时进行；关系式(22)对应式(20)正确的原因在于，它能导出Gq(n0)=16Gq(Ω0)，与国标一致。

1.4 空间域路面不平度位移标准差计算

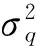
(23)

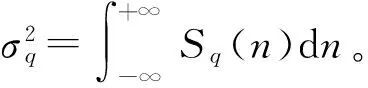
统计显示路面空间频率分布于[0.011 2.83] m-1区间,在常用车速下(10～30 m/s)下，激励的时间频率(车速与空间频率乘积)分别为[0.11 28.3]和[0.33 84.9] Hz，两区间交集为[0.33 28.3] Hz，涵盖了车身(1～2 Hz)和车轮(10～20 Hz)的固有频率，适合做汽车平顺性分析的输入。根据国家标准，A级路面不平度系数几何均值为16×10-6m3，则其不平度路面标准差为

(24)

验证依据GB/T 7031-2005，国标附录C中表C.3列出不同等级道路位移功率谱密度的几何均值和限值，对于A级道路，对应于空间中心频率为0.015 6，0.031 2，0.062 5，0.125，0.25，0.5，1和2 m-1的倍频段的单边位移功率谱密度几何均值分别为655×10-6，164×10-6，41×10-6，10.2×10-6，2.56×10-6，0.64×10-6，0.16×10-6和0.04×10-6m3。

中心频率点0.015 6，2 m-1对应的倍频段分别为[0.011 0 0.022 1]，[1.414 2 2.828 4] m-1，可见，自0.015 6到2 m-1的倍频带刚好涵盖了路面信号的频率范围[0.011 2.83] m-1，对其中各倍频段位移功率谱密度几何均值求和开方可求得A级路面平均标准差，约等于3.78 mm。

可见式(24)的计算结果与标准值近似相等，从而验证了空间频率和角频率功率谱密度的关系(即式(17)与式(13)对应)的正确性。

另外，如果在时间域计算标准差，如式(25)，(26)所示，结果与式(24)相同，说明路面均方根与车速和计算所在域无关。

(25)

(26)

2 傅里叶逆变换法路面模拟

要从频域数据合成路面信号，必须知道幅值谱和相位谱。统计分析发现路面相位谱服从[0 2π]的均匀分布，可由函数随机生成。基于功率谱密度离散化的路面建模方法，就是要由已知的标准等级路面功率谱密度计算出信号的幅值谱，进而由傅里叶逆变换法得到路面不平度信号。

傅里叶变换有多种类型：周期连续信号傅里叶级数(FS)、周期连续信号傅里叶变换、非周期连续信号傅里叶变换(FT)、离散时间非周期信号傅里叶变换、离散傅里叶变换(DFT)和周期离散信号傅里叶级数(DTFS)。只有DFT和DTFS在时、频域均离散，并且二者定义完全相同，DTFS是DFT的周期延拓，计算机只做DFT。2.2节将证明DFT变换结果可看作信号幅值谱，用于路面信号合成。

2.1 功率谱密度离散化的原因及目的

路面不平度可看作各态历经随机信号，取长度为L的一段路面qL(l)，根据式(4)可知，路面信号的单边功率谱密度估计为

(27)

qL(l)为空间域有限的非周期连续信号，其傅里叶变换是连续值，分布在整个空间频域，理论上其幅值谱(相当于周期信号傅里叶级数的傅里叶系数)趋于零，由式(4)和(27)知Q(n,L)是信号的幅值谱密度，而信号合成需要的是幅值谱Q(k)，故不能直接用来合成信号。

虽然理论上其幅值谱趋于零，但有效路面数据只是[0L]这一段，将其周期延拓成为周期为L的周期信号，满足狄利克雷条件，傅里叶级数存在，可以由傅里叶级数(即幅值谱)合成一个周期[0L]的路面不平度信号，如式(28)所示，这里Ω0=2π/L为空间角频率(基频)。

(28)

为了适应计算机处理，将周期延拓的路面不平度信号进行等周期采样，则信号成为周期离散时间信号，于是其时、频域均离散，从而可以由DFT的定义式(29)求出路面不平度信号的幅值谱Q(k)。

(29)

将Q(n,L)积分形式表示成N项级数和，与离散傅里叶变换Q(k)产生换算关系。

大多数商圈只注重交易数据而忽视购买群体的过程数据，而这部分数据正是挖掘商机的入口。图1为商圈客流分析功能示意,其中客流分析项是对商圈日常的经营数据和客流数据进行汇总得到的，这些数据的处理和分析对于商圈运营者而言可进行更为细致的分析。客流数据分析系统需结合交易数据和过程数据获取有价值的数据。研究结果证明，只有0.5%～3.0%的人在网上点击广告之后会真正购买相应的产品,而消费者走进实体商店购买的概率则大很多。对于商圈管理者来说，该部分数据的价值分析示意见图2。

(30)

其中：Δn=1/(NΔl)，为空间频率分辨率。

从以上分析可看到，功率谱密度离散化本质是将截断路面信号的幅值谱密度离散化，得到延拓周期信号的傅里叶级数，以此来合成路面信号。

2.2 离散化结果验证

功率谱密度离散化的目的是得到信号的幅值谱，那么Q(k)是不是路面不平度离散周期信号的幅值谱？下面从周期连续信号傅里叶级数(式(28))出发来给以验证。

将长度和周期均为L的路面不平度连续信号的傅里叶级数近似表达成M项级数和的形式，可得到连续周期信号傅里叶级数与DFT的关系

(31)

可以看出离散傅里叶变换Q(k)与幅值级数Ck只存在一个系数差别，这个系数将在逆变换时得以消除，故Q(k)可以代表信号幅值谱。

亦可如此分析,假设信号qL(l)长度和周期L均为无穷大，根据幅值谱和幅值谱密度的关系得到

(32)

对路面qL(l)在一个周期内等间隔采样N点，根据频域卷积定理，信号频谱被延拓成N个，路面客观存在，即傅里叶级数不变，于是得到

(33)

(34)

比较式(30)和式(34)发现，Q(k)即为信号幅值谱。采样点数N的取值可以参考文献[9]。

2.3 频谱点对称设置

根据上述分析，离散功率谱密度估计式为

(35)

信号幅值谱为

(36)

其中：dn=1/L，为空间频率分辨率，即采样路面总长度的倒数。

相位角在[0 2π]上均匀分布，在Matlab中可以由unifrnd函数生成。然后根据式(36)通过傅里叶逆变换生成路面空间域随机信号。

离散傅里叶变换Q(k)的第一个点(直流分量)不存在对称。对于模拟路面数据N，如果是偶数，则关于N/2+1点对称；若为奇数，则关于(N+2)/2点对称，根据式(36)生成幅值谱Q(k) (k=1,…,N/2+1或(N+1)/2)。则另一半幅值频谱数据为

Q*(N/2)，Q*(N/2-1)，…，Q*(2) (N为偶数)；Q*((N+1)/2),…,Q*(2) (N为奇数)。

Q*(k)表示Q(k)的共轭复数，将两段频谱数据组合后进行离散傅里叶逆变换即可得到路面信号。

3 功率谱密度验证

正确的模拟路面除了要满足均值和标准差的条件外(即均值接近于零；标准差与标准值接近并不随车速、采样频率和仿真时间改变)，功率谱密度曲线的趋势必须与国标和ISO文件要求一致[10]。

3.1 功率谱密度验证方法

计算模拟路面的功率谱密度时，不少文献采用了直接法[9]，这是不准确的。因为直接法采用的计算式为式(35)，本质上是上述计算的逆过程，这样得到的功率谱密度数值与标准值完全相同，如图1所示，模拟路面的谱曲线与ISO标准路面谱曲线完全重合，验证没有意义，不能真实反映程序模拟路面的频域特性。

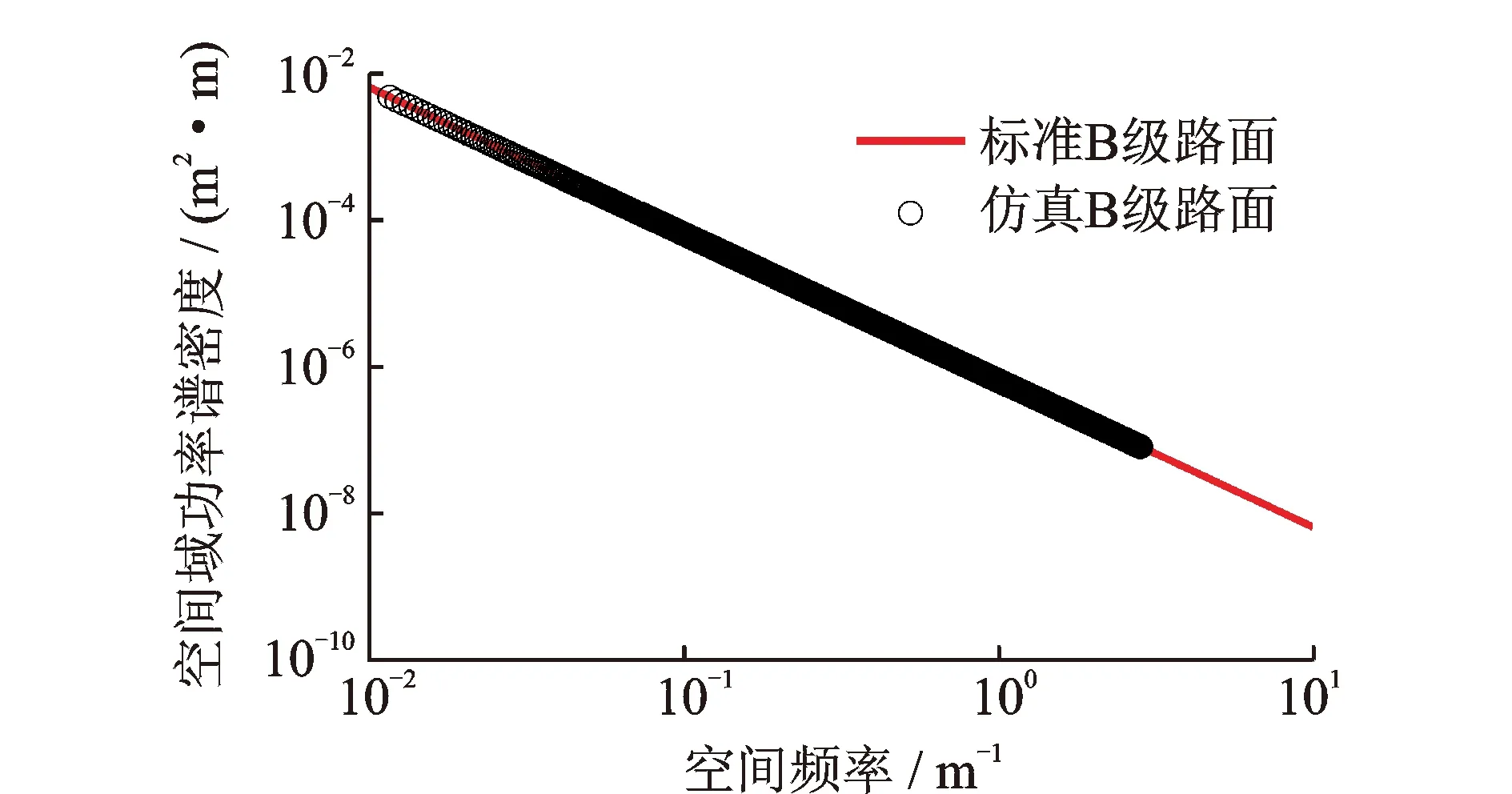
图1 直接法功率谱密度计算Fig.1 PSD calculated by direct computation method

经典谱估计的平均周期图Welch法，对路面信号分段，段间适当重叠，分段计算功率谱密度再平均，通过窗函数减小信号分段造成的能量向旁瓣泄漏，窗函数造成的信号能量衰减，已在函数内部进行了修正，Welch法能更真实地反映模拟路面信号功率在频率轴的分布特征。

3.2 两种采样频率的应用

平均周期图法谱估计函数pwelch调用格式为：[Pxx,F]=pwelch(signal,window,overlap,NFFT,fs,'oneside')，有两种采样频率：空间域采样频率ns和时间域采样频率fs，令车速为u，采样时间间隔为Δt，则时间和空间频率分别为：fs=1/Δt，ns=1/(uΔt)。

窗函数选择，国标推荐用汉宁窗，这其实是在频率分辨率和能量泄漏之间取的一个较理想折中方案，这里灵活采用切比雪夫窗，旁瓣衰减100 dB，能量泄漏减小，但频率分辨力下降，谱曲线趋于平滑。

窗函数通常应用于滤波器设计和谱估计，它们对窗函数的要求有差异：谱估计防止能量泄漏，希望窗函数频谱旁瓣较小；滤波器设计通常要求过渡带较小，要求窗函数主瓣陡峭，但有关指标是矛盾的，需要折中，详细的选择方法可参考有关教材。

采用空间域采样频率ns将得到空间域路面不平度位移功率谱密度Gq(n)，同时输出的频率点是空间频率；如果采用时间域采样频率fs，则得到时间域的频率点和相应的时域功率谱密度Gq(f)。

3.2.1 空间域路面不平度位移功率谱密度

应用Welch法对模拟路面信号Xm进行单边功率谱密度估计，根据上述分析，编制Matlab程序如下，运行结果如图2所示。

NFFT=2^nextpow2(round(length(Xm)/4));

window=chebwin(NFFT); %切比雪夫窗函数

overlap=round(length(Xm)/8); %段间重叠

ns=ceil(N/L); %空间采样频率

[Pxx,F]=pwelch(Xm,window,overlap,NFFT,ns,'oneside'); %采用空间采样频率做功率谱密度估计

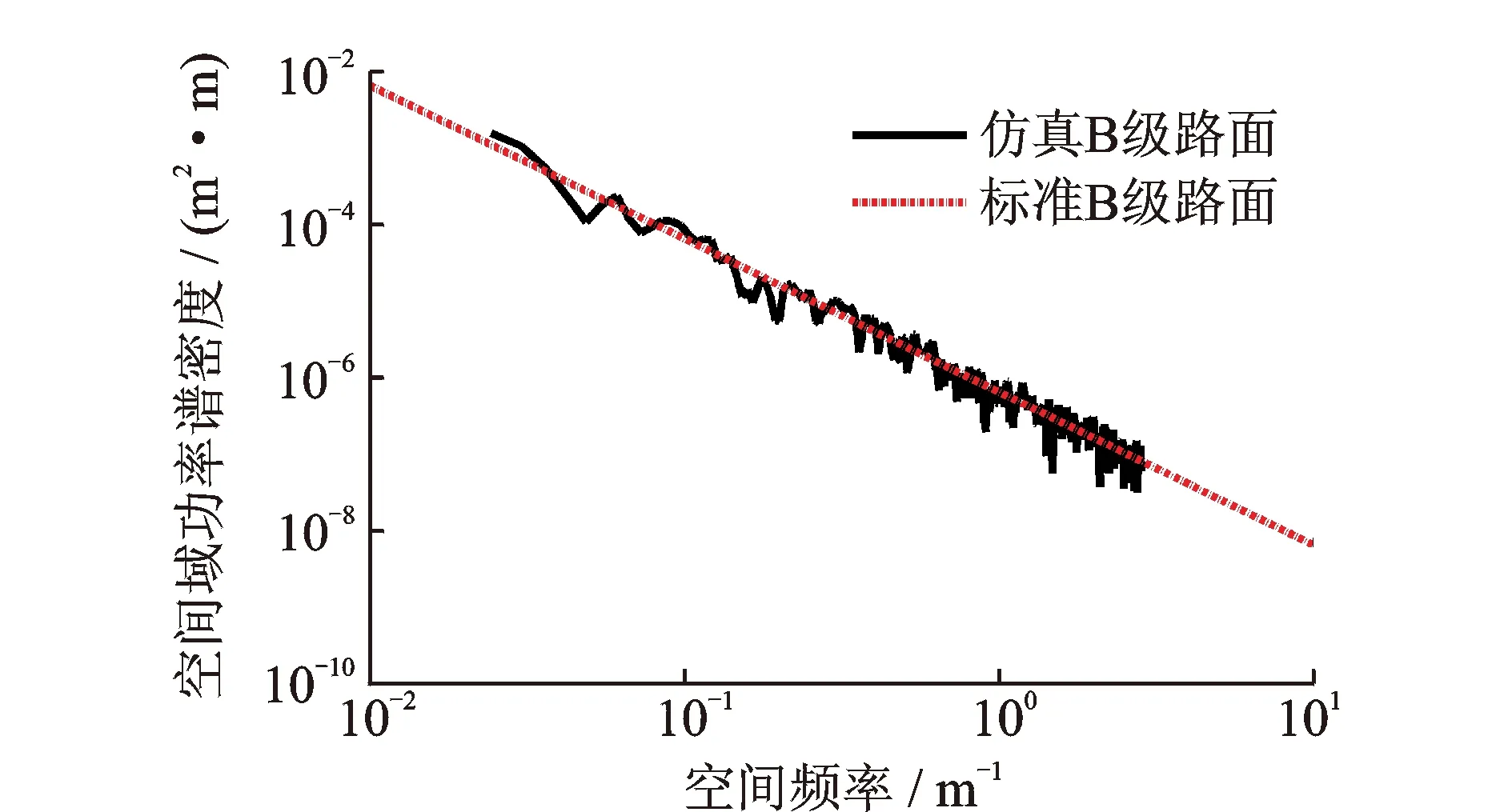
图2 采用空间采样频率的Welch法输出Fig.2 Output of Welch with spatial sampling frequency

图2中虚线为B级路面位移功率谱密度函数曲线，数学函数为Gq(n)=64×10-6×(n/0.1)-2，在双对数坐标中为一直线；程序中ns为空间采样频率，图中实线为模拟路面功率谱密度曲线，在标准曲线上下波动，趋势一致，说明采用空间采样频率得到的是空间域功率谱密度。

3.2.2 时域路面不平度位移功率谱密度

采用时间采样频率，将程序参数ns改为时域采样频率fs，运行程序得到图3。

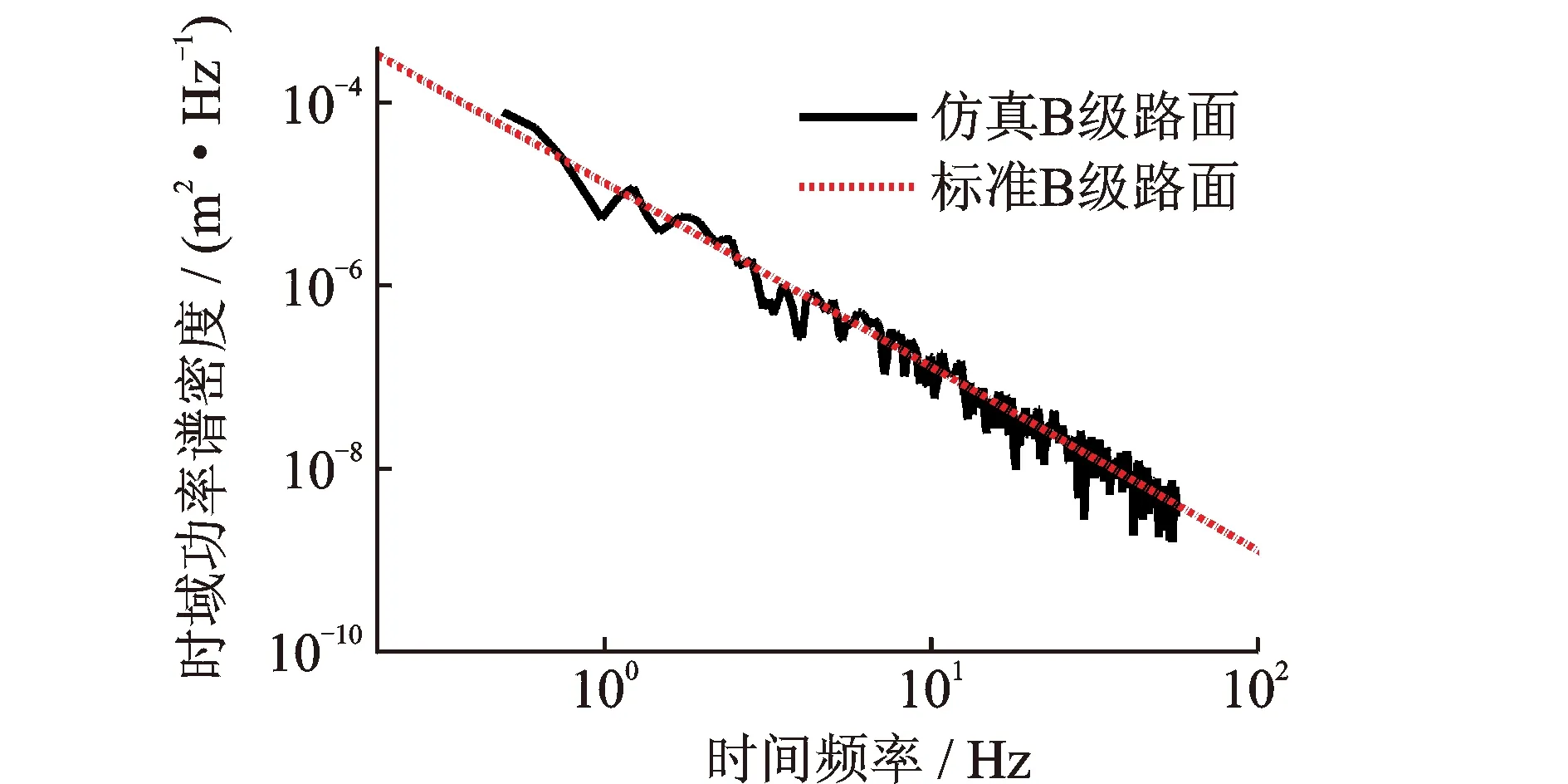
图3 采用时间采样频率的Welch法输出Fig.3 Output of Welch with temporal sampling frequency

车速u为20 m/s，时间频率f=20n，即输出的频率序列F为时域点，故图2和图3的横坐标不同。图3的虚线数学函数为Gq(f)=Gq(n)/u=3.2×10-6×(n/0.1)-2，为车速20 m/s下B级标准路面的时域功率谱密度，图3显示模拟路面的功率谱密度与标准时域功率谱密度一致，故可知pwelch函数采用时间采样频率时输出的功率谱密度和频率点均为时域。

如果要换算成空间域的功率谱密度，根据空间与时间域频率和功率谱密度的关系，需将输出的频率向量F除以车速u，相应的功率谱密度Pxx乘以车速。

4 结束语

以帕塞瓦尔定理和维纳-辛钦定理为基础，分析了路面空间域自相关函数和功率谱密度的计算方法，推导出路面不平度空间域位移、速度和加速度功率谱密度之间，以及空间频率与空间角频率功率谱密度之间换算关系。应用傅里叶级数和变换、离散傅里叶变换、离散时间傅里叶级数理论和频域卷积定理，详细分析论证了傅里叶逆变换路面建模方法的功率谱密度离散化问题。指出了直接法功率谱密度验证的不合理之处，论证了平均周期图法谱估计时应用空间采样频率将输出路面空间域PSD，而时间采样频率对应着路面时间域PSD输出。理论分析以及与国标和ISO标准的对比验证显示，文中的研究是正确的，可用于路面不平度建模和汽车平顺性分析。

[1] Bogsjö K, Podgórski K, Rychlik I. Models for road surface roughness [J]. Vehicle System Dynamics, 2012, 50(5): 725-747.

[2] Mucka P. Influence of road profile obstacles on road unevenness indicators [J]. Road Materials and Pavement Design, 2013, 14(3): 689-702.

[3] 黄雪涛，顾亮，吕唯唯. 轻型载货汽车减振技术分析及优化分析[J]. 振动、测试与诊断，2013, 33(2): 315-318.

Huang Xuetao, Gu Liang, Lv Weiwei. Vibration reduction technology analysis and optimal design on lighttruck [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 315-318. (in Chinese)

[4] International Organization for Standardization. ISO 8608—1995(E), Mechanical vibration-road surface profiles-reporting of measured data [S]. Geneva: Int. Standard Organization, 1995.

[5] 全国机械振动与冲击标准化技术委员会. GB/T 7031—2005 机械振动——道路路面谱测量数据报告[S].北京:中国标准出版社,2006.

[6] Agostinacchio M, Cinampa D, Olita S. The vibrations induced by surface irregularities in road pavements-a Matlab®approach [J]. European Transport Research Review, 2014, 6(3): 267-275.

[7] 卢士富. 关于平稳过程自谱密度运算中的两个问题[J]. 西安公路学院学报，1991,11(2): 54-61.

Lu Shifu. On two problems in calculating self-spectrum density of smooth process [J]. Journal of Xi′an University of Highway, 1991, 11(2): 54-61. (in Chinese)

[8] Zhang Yonglin, Zhang Jiafan. Numerical simulation of stochastic road process using white noise filtration [J]. Mechanical Systems and Signal Processing, 2006, 20(2): 363-372.

[9] 刘献栋，邓志党，高峰. 基于逆变换的路面不平度仿真研究[J]. 中国公路学报，2005,18(1): 122-126.

Liu Xiandong, Deng Zhidang, Gao Feng. Study of simulation of road roughness based on inverse transform [J]. China Journal of Highway and Transport, 2005, 18(1): 122-126. (in Chinese)

[10]Durst P J, Mason G L, McKinley B, et al. Predicting RMS surface roughness using fractal dimension and PSD parameters [J]. Journal of Terramechanics, 2011, 48(2): 105-111.

10.16450/j.cnki.issn.1004-6801.2015.05.030

2014-09-24；

2014-12-01

TH113.1; U461.5+6; TP391.9

杜峰，男，1980年5月生，博士生。主要研究方向为汽车平顺性仿真及客观评价。曾发表《PSD和PWELCH函数的分析改进及应用》(《中国测试》2010年第36卷第1期)等论文。 E-mail：dufeng123dufeng@126.com