基于向量自回归模型的损伤识别方法*
刘 纲, 罗 钧, 方 鹏, 秦 阳
(1.重庆大学土木工程学院 重庆,400045) (2.山地城镇建设与新技术教育部重点实验室 重庆,400030)
基于向量自回归模型的损伤识别方法*
刘 纲1,2, 罗 钧1, 方 鹏1, 秦 阳1
(1.重庆大学土木工程学院 重庆,400045) (2.山地城镇建设与新技术教育部重点实验室 重庆,400030)
基于向量自回归(vector auto-regression,简称VAR)模型,提出了一种能同时进行损伤定位和程度识别的时间序列方法。首先,利用测试的加速度响应时程信号建立VAR模型,提取模型系数的对角线元素作为损伤敏感向量,并采用该向量的马氏距离作为损伤特征值;然后,应用统计模式识别手段,通过受试者工作特征曲线下的面积指标来判别损伤是否出现及其部位,并通过Bhattacharyya距离来度量损伤程度。数值模拟和实验室框架模型实验表明,该算法能成功识别损伤部位和损伤程度的相对大小,且具有较好的抗噪性能,为结构长期在线损伤识别提供了一种有效手段。
损伤识别; VAR模型; 受试者工作特征曲线; Bhattacharyya距离
引 言
承受荷载的结构体系在日常环境和运营荷载作用下将逐步老化或损伤。为延长结构的使用寿命,降低结构日常维护费用并预防倒塌等恶性事故的发生,业界提出了较传统的定期维护和人工检查更为先进合理的基于结构性能状态的维护策略,从而促进了健康监测在土木工程中的快速发展[1-2]。
目前,基于振动的损伤识别方法已成为健康监测领域内的一个主流研究方向,可大致分为基于模态驱动的方法和基于数据驱动的方法。基于模态驱动的方法通常采用识别得到的频率、振型等模态指标以及模态柔度、模态应变能等衍生指标识别损伤是否发生以及损伤部位,并可进一步结合模型更新等手段量化损伤程度[3-4]。目前,国内外学者已针对该类方法进行了大量研究,很多算法已在实验室结构和小型结构上得到成功验证或初步应用[5],但该类方法对结构局部损伤不敏感,仅在风、地脉动等环境激励下辨识得到的模态指标的不确定性较大,大型复杂结构的基准有限元模型较难准确获取从而限制了该类方法的应用范围。
基于数据驱动的方法多借助于自回归(autoregressive, 简称AR)、滑动自回归、小波变换和希尔伯特黄变换等数学模型从结构响应信号中提取损伤判别指标[6-8],然后通过结构损伤前后指标的统计模式对比实现损伤识别。例如,文献[9]采用AR模型前三阶系数构建损伤判别指标并通过AR系数张成的空间构建损伤定位指标,然后通过统计检验的方式,成功识别了美国土木工程协会的四层钢框架结构的损伤。文献[10]利用某传感器的信号作为输出,其临近传感器的信号作为输入来建立外部输入自回归模型,在统计分析模型预测误差的基础上利用Fisher准则构建损伤判别指标,通过对所有传感器依次计算实现结构损伤部位和程度的识别,并采用格构式钢梁验证了该算法的有效性。文献[11]采用自回归-支持向量机为模型,通过损伤前后模型预测误差的方差之比建立损伤识别指标,再通过F检验判定结构是否出现损伤,该算法能顺利识别非线性结构的损伤,但其定位功能较弱。
基于数据驱动方法的计算速度快,能实时完成损伤识别且相对于模态方法更易应用于大型结构中[12]。损伤识别可划分为递进的四层次问题,即判定结构有无损伤、损伤部位、损伤程度和剩余寿命[2]。当前的时域方法多关注于判断结构有无损伤,仅能满足损伤识别第一层次的要求[10],或者通过各传感器的不同组合,循环计算实现损伤部位和程度的判定,这虽然达到了损伤识别第二和第三层次的需求,但会增大计算工作量从而降低损伤识别的实时性。
针对以上不足,笔者首先利用向量自回归模型系数矩阵的对角线元素提取新向量,采用结构损伤前后新向量的马氏距离构造损伤识别指标;然后,基于受试者工作特征曲线下的面积和Fisher准则两种统计手段,实现结构损伤程度和部位的判别,从而通过一次计算可同时解决损伤识别前三个层次的问题;最后,通过6自由度数值模型和实验室两层钢框架实验验证了算法的有效性。
1 VAR时间序列模型及阶数选取
1.1 VAR时间序列模型
1980年,Sims首先提出了向量自回归模型,该模型描述了n个不同变量之间的线性演化关系,一个p阶VAR模型的定义[13]为
yt=c+A1yt-1+…+Apyt-p+et
(1)
其中:yt={y1t,y2t,…,ynt}T为由n个变量组成的列向量;Ai为n×n阶系数矩阵;c为插值向量,表示数据的整体偏移。
损伤识别中,数据首先会进行零均值归一化预处理,故该项通常为零,可省略;et为误差项,是均值为零、方差确定的向量。
经整理,式(1)可简写为
Y=BZ+E
(2)
其中:Y=[y1,y2,…,yT],为n×T的矩阵;T为计算数据的点数;B=[A1,A2,…,Ap],为n×np的矩阵;Z=[Z0,Z1,…,ZT-1],Zt={yt,…,yt-p+1}T为np×1的列向量;E=[e1,e2,…,eT],为n×T的矩阵。
采用最小二乘法可得式(2)中系数项B的估计为
⊗In)Y
(3)
向量自回归模型能够描述结构体系动态响应的原因在于其与结构运动方程具有较好的对应关系,简要说明如下:对于多自由度体系,假设在离散时间点ti(ti=iΔt,Δt为采样间隔;i=1,2,…,T),考察结构的运动方程
(4)
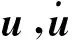
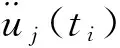
(5)
将式(5)代入式(4),经整理可得
(6)
将式(6)右边中括号内的系数项分别用矩阵B1,B2和B3表示,并令k=ti+1,则式(6)可简写为
u(k)=B1u(k-1)+B2u(k-2)+B3Fp(k-1)
(7)
对比式(1)和(7)可知,VAR模型中的A1,A2分别与结构运动方程中的B1,B2相对应,故VAR模型在理论上与结构运动方程具有一定的一致性。当用VAR模型描述结构系统的运动时,结构刚度或阻尼的改变(B1,B2)将在VAR模型中引起系数矩阵(A1,A2)的变化,故可通过结构损伤前后VAR模型系数的改变来识别结构的损伤。
1.2 模型阶数的选取
从式(7)可知,当输入已知时,二阶VAR模型能较好地拟合结构的响应,但土木结构很难人为施加激励,故输入项无法准确获取。通常而言,假设结构运营环境下的输入为白噪声,此时可通过增大模型阶数来拟合未知的输入,但阶数过大将引发过拟合现象。这一不足可通过VAR模型阶数判定准则解决。笔者选取较为常用的赤池信息准则(akaike information criterion,简称AIC)准则,其定义[13]为
AIC(p)=ln(|Σ(p)|)+2pn2/T
(8)
其中:Σ(p)表示模型阶数为p时残差协方差矩阵。
计算不同阶数下的AIC值,选取AIC值最小所对应的阶数为模型的最优阶数,此时VAR模型将在较小阶数的情况下最好地拟合数据。
2 损伤特征指标及识别流程
2.1 损伤特征指标
当结构某处发生损伤时,该处的刚度将降低,故在形成结构总体刚度矩阵时,与该部位各自由度对应的主对角线元素和非对角线元素的值将减少,而其余各元素保持不变。对于一个自由度为n的结构体系,刚度矩阵非主对角线元素的数量是主对角线元素数量的(n-1)倍,而仅有少量元素包含损伤单元的信息,所以从提高计算效率角度出发,可仅用主对角线元素进行损伤识别。在式(6,7)中,结构刚度矩阵主对角线元素对应于B1,B2矩阵中的主对角线元素(以瑞雷阻尼假定为例,刚度矩阵的变化将引起阻尼矩阵的变化,故B2矩阵中虽无刚度项,但损伤也会引起其发生改变)。结合式(1)可知,VAR模型中系数矩阵的主对角线元素将随结构的损伤而发生变化,因此提取VAR模型中各系数矩阵Ai(i=1,2,…,p)的主对角线元素为新向量f
(9)
新向量f的元素较多(n×p),为高维向量,采用马氏距离对其进行降维,从而建立损伤识别特征指标MD[4]为
(10)
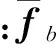
2.2 统计模式识别
选取受试者工作特征曲线和Fisher准则分别进行损伤部位和程度的判定。受试者工作特征曲线(receiver operating characteristic curve,简称ROC曲线)[14]是二次世界大战中为评估雷达辨识目标的性能而提出的信号检测理论。当得到结构损伤前后损伤特征指标的分布曲线并选取决定阈值后,就能确定该阈值下损伤特征指标检测损伤的性能,如图1所示。例如假阳性率为结构处于完好状态但阈值的判定结果却为损伤的概率,即误报警率。
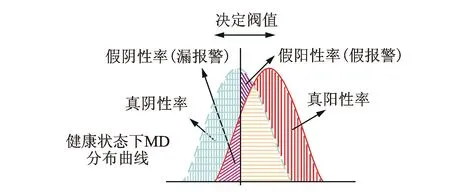
图1 信号统计检测Fig.1 Signal statistical detection
选取不同的阈值,将得到不同的假阳性率。为避免人为确定阈值带来的误差,ROC曲线是以假阳性率为横坐标,真阳性率为纵坐标,然后在选取不同决定阈值下所做出的曲线。通常采用ROC曲线下的面积值(area under ROC curve,简称AUC)作为统计量来评价检测的性能。AUC的取值在0.5~1之间。当AUC≥0.8时,表明判定结果的准确性较高;当0.7>AUC时,表明判定结果的准确性低。
通过损伤测点处MD分布的B氏距离(Bhattacharyya distance,简称BD)判断损伤程度,对于单变量指标,BD定义[15]为
(11)
其中:κ和σ分别表示MD分布的平均值和方差,下标d和h分别表示损伤状态和基准状态。
从式(11)的定义可知,前一项主要考虑了均值变化的影响,而后一项主要是为了计入方差变化的影响。
2.3 损伤识别流程
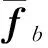
3 数值模拟算例
3.1 模型算例及损伤工况
以6自由度集中质点模型检验算法的性能,如图2所示。其中:mi=1;ki=1 500 (i=1,2,…,6)。模型采用瑞雷阻尼假定,即C=αM+βK,任取2阶模态阻尼比即可确定阻尼矩阵,随机选取模型第1阶和第3阶阻尼比为0.02,计算得α=0.308 09,β=7.5×10-4。

图2 6自由度计算模型Fig.2 Six degree-of-freedom system
在质点6处输入随机激励,取质点1~6处的加速度响应为输出信号。拟定的损伤工况如表1所示。

表1 6自由度体系的损伤工况
因该体系的最高频率为11.97 Hz,取加速度信号的采样频率为100 Hz,并设定每1 000个数据点为1个数据段。在基准状态、参考状态和未知状态下分别取1 000个数据段进行计算,可得到1 000个MD值。
取基准状态下各质点的100段数据,采用AIC准则计算模型的阶数,得到VAR模型的合理阶数范围为5~15,取5阶VAR模型VAR(5)进行损伤识别计算,然后分析模型阶数对损伤识别性能的影响。
3.2 损伤识别结果
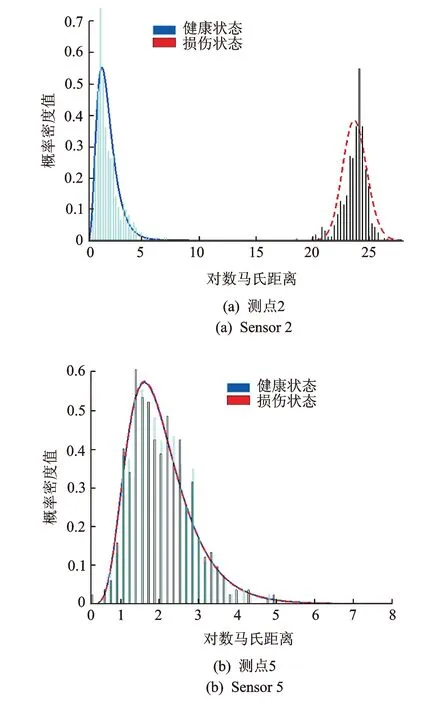
图3 损伤工况1下部分测点的MD分布曲线Fig.3 MD distribution under damage case 1 for partial sensors
体系在损伤工况1下部分测点的MD分布曲线如图3所示。图中的柱状图为1 000个MD值的频数分布直方图,曲线为其拟合的对数正态分布(在0.05的显著水平下,采用柯尔莫可洛夫-斯米洛夫假设检验MD的频数分布直方图为对数正态分布)。从该图可知,仅在损伤附近质点处的MD分布才发生变化,而其余测点处MD分布的变化较小,采用ROC曲线对MD分布是否发生显著变化进行检验,并计算ROC曲线下的面积AUC(见表2)。
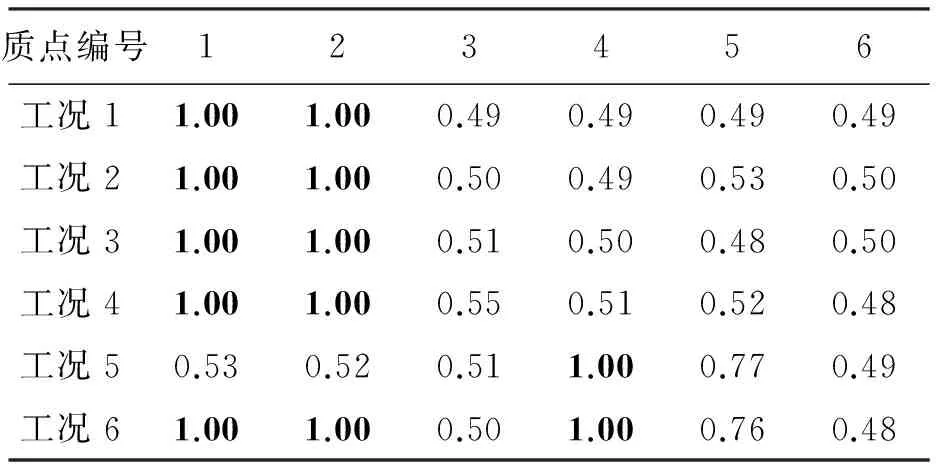
表2 各损伤工况下的AUC值
根据AUC的定义,笔者选取0.85为能否良好区分损伤是否发生的阈值。表2表明,在各损伤工况下,仅在损伤附近质点的AUC值才高于0.85(在表中以黑体标注),而其余质点的AUC值均低于0.85。因此,该指标不但能够成功定位损伤程度较小(1%)的单处损伤,也能定位工况6下不同部位发生的损伤。
为识别弹簧2发生的不同程度的损伤,计算质点1,2在工况1~4下的BD值如图4所示。图4表明,随着损伤程度的增加,质点1,2的BD值均呈单调上升趋势,即BD值能正确区分损伤程度的相对大小。

图4 不同损伤程度下的BD值Fig.4 BD values under different damage levels
3.3 噪音影响分析
图5为不同噪音水平下质点1和质点2处的AUC值。随着噪音水平的不断增大,损伤定位的准确性将降低,特别是当结构损伤程度较小时,噪音的影响较为显著。例如工况2下,当噪音水平为10%时出现了漏报警;但随着损伤程度的增加,噪音的影响将逐步减小甚至消失。例如在工况5下,即使20%的噪音水平也完全能定位出质点1,2处的损伤,表明基于VAR模型的损伤识别算法具有较好的抗噪性能。

图5 不同噪音水平下的AUC值Fig.5 AUC values under different noise levels
质点1在不同噪音水平下的BD值如图6所示。该图显示在同一损伤工况下,随着噪音水平的不断升高,对应的BD值将越来越低。但在同一噪音水平下,随着损伤程度的增加,BD值呈单调上升趋势,表明此时仍能正确区分损伤程度的大小。

图6 不同噪音水平下的BD值Fig.6 BD values under different noise levels
3.4 模型阶数影响分析
考察模型阶数对损伤识别算法的影响,计算15阶VAR(15)模型的AUC值如表3所示。该模型的AUC值将在较多质点处大于0.85(在表中以黑体标注),即出现损伤部位的误判,故应取AIC准则判定的较小阶数建立VAR模型。
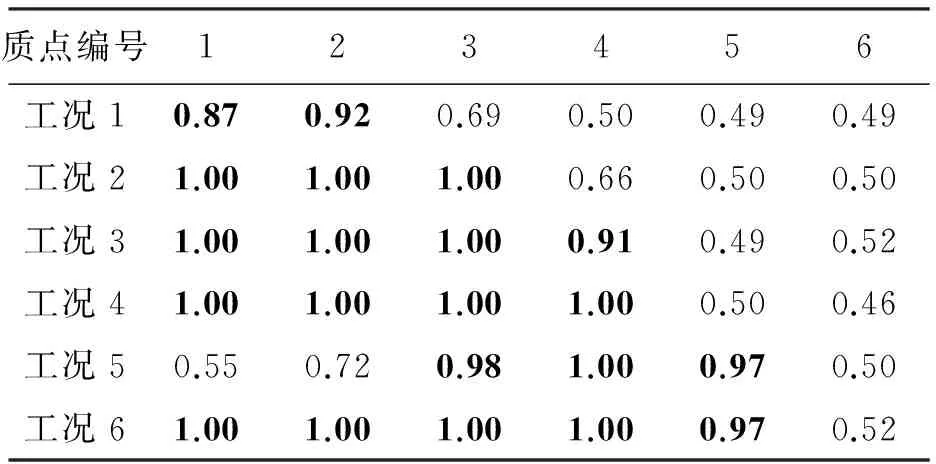
表3 VAR(15)模型的AUC值
VAR(10)和VAR(15)模型在工况1~4下的BD值如图7所示。

图7 不同VAR模型阶数的BD值Fig.7 BD values for different VAR model orders
在模型阶数相同的情况下,BD值仍随损伤程度的增加而单调递增,因此VAR模型阶数的选取不影响损伤程度的识别。
4 实验室框架实验
框架采用宽为50.8 mm,厚为3.175 mm的钢板组成梁和柱,并通过节点板和螺栓进行连接,其外观尺寸如图8所示。每个节点板共安装4颗螺栓,2颗与柱相连,2颗与梁或刚性基座相连。试验中通过第2层右柱顶的螺栓松动模拟损伤,故沿该侧柱布置6个加速度传感器,从上到下依次编号为1~6。

图8 两层框架模型Fig.8 The 2-story steel frame
采用PM50A型电磁激振器在第1层左柱下侧输入白噪声激振。加速度传感器的采样频率设为5 120 Hz。为模拟逐步损伤过程,依次松动第2层右柱顶的螺栓。具体的损伤工况设置如表4所示。

表4 框架的损伤工况
计算的AUC值如表5所示。在工况3和工况4下,仅传感器1和传感器2的AUC值高于阀值0.85,其余传感器的AUC值均小于0.65,这一结果与结构实际损伤部位相符,因此在这两个工况下可以准确判定损伤部位。在工况2下,虽传感器1和2的AUC值低于0.85,但仍较其余传感器处的AUC值大。这可能是因为实验框架受力较小,仅松动一颗螺栓对结构影响较小,从而导致该工况下AUC值在损伤部位的变化不大。

表5 实验模型的AUC值
计算传感器1在工况2~4下的BD值分别为1.32,3.58和7.83。 这表明BD值随着损伤程度的增加而单调增加,因此通过BD值的计算能正确判定结构的损伤程度。
5 结 论
1) 基于VAR模型的损伤识别算法能够正确定位结构的单处损伤和多处损伤,并能够准确区分损伤程度的相对大小。
2) 当损伤程度较小时,算法可能出现漏报警,例如发生1%损伤时,在10%的噪音水平将无法识别损伤;但当损伤程度增大后,将大幅提高算法的损伤定位能力,例如发生10%损伤时,即使20%的噪音水平也能有效实现损伤定位。同时,噪音不影响损伤程度的识别。
3) 针对基准状态下的不同数据,AIC准则将得出不同的VAR模型阶数。较大的模型阶数将导致损伤部位的误判,故所提算法宜采用较小的VAR模型阶数进行损伤识别。
[1] Sohn H, Farrar C R, Hemez F M, et al. A review of structural health monitoring literature:1996-2001 [R]. Los Alamos:Los Alamos National Laboratory, 2004:5-8.
[2] Farrar C R, Worden K. An introduction to structural health monitoring [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical & Engineering Sciences, 2007,365(1851):303-315.
[3] 冯新,李国强,范颖芳. 几种常用损伤动力指纹的适用性研究[J].振动、测试与诊断,2004,24(4):277-280.
Feng Xin, Li Guoqiang, Fan Yingfang. Suitability study on dynamic signatures used in structural damage localization [J]. Journal of Vibration, Measurement & Diagnosis, 2004.24(4):277-280. (in Chinese)
[4] Tee K F, Koh C G, Quek S T. Numerical and experimental studies of a substructural identification strategy [J]. Structrual Health Monitoring, 2009,8(5):397-410.
[5] 宗周红,褚福鹏,牛杰. 基于响应面模型修正的桥梁结构损伤识别方法[J]. 土木工程学报,2013,46(2):115-122.
Zong Zhouhong, Chu Fupeng, Niu Jie. Damage identification methods of bridge structures using response surface based on finite element model updating[J]. China Civil Engineering Journal,2013,46(2):115-122. (in Chinese )
[6] 吴森,韦灼彬,王绍忠,等. 基于AR模型和主成分分析的损伤识别方法[J]. 振动、测试与诊断,2012,32(5):841-845.
Wu Sen, Wei Zhuobin, Wang Shaozhong, et al. Damage identification based on AR model and PCA [J]. Journal of Vibration, Measurement & Diagnosis,2012,32(5):841-845. (in Chinese )
[7] 赵学风,段晨东,刘义艳,等. 基于小波包变换的支持向量机损伤诊断方法[J]. 振动、测试与诊断,2008,32(6):104-107.
Zhao Xuefeng, Duan Chendong, Liu Yiyan, et al. Diagnosis of structure damage by support vectorMach ine based on wavelet packet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2008,32(6):104-107. (in Chinese)
[8] 熊飞,程远胜,刘均. 基于HHT 方法的时变多自由度系统的损伤识别[J]. 振动、测试与诊断,2009,28(2):122-125.
Xiong Fei, Cheng Yuansheng, Liu Jun. Damage identification of time vary ing multi-Degrees of freedom system based on hilbert-huang transform [J]. Journal of Vibration, Measurement & Diagnosis, 2009,28(2):122-125. (in Chinese)
[9] Nair K K, Anne S K, Kincho H L. Time series-based damage detection and localization algorithm with application to the ASCE benchmark structure [J]. Journal of Sound and Vibration, 2006,291(1):349-368.
[10]Bornn L, Farrar C R, Park G. Damage detection in initially nonlinear systems [J]. International Journal of Engineering Science, 2010,48(10):909-920.
[11]Yao R, Pakzad S N. Autoregressive statistical pattern recognition algorithms for damage detection in civil structures [J]. Mechanical Systems and Signal Processing, 2012,31(8):355-368.
[12]Mustafa G, Catbas N. Statistical pattern recognition for structural Health Monitoring using time series modeling: theory and experimental verifications[J]. Mechanical Systems and Signal Processing,2009,23(7):2192-2204.
[13]Lütkepohl H. New introduction to multiple time series analysis[M]. New York:Springer,2005:23-58.
[14]Søreide K. Receiver-operating characteristic curve analysis in diagnostic, prognostic and predictive biomarker research [J]. Jouanl of Clinical Pathology, 2009,62(1):1-5.
[15]Choi E, Lee C. Feature extraction based on the Bhattacharyya distance [J]. Pattern Recognition,2003,36(8):1703-1709.

10.16450/j.cnki.issn.1004-6801.2015.05.011
*重庆市自然科学基金资助项目(CSTC2012JJA30006);中央高校基金资助项目(CDJRC10200018, CDJZR14205501)
2013-09-10;
2013-11-21
TU279.7+44
刘纲,男,1977年1月生,博士、副教授。主要研究方向为结构健康监测和振动控制。曾发表《Damage assessment with state-space embedding strategy and singular value decomposition under stochastic excitation》(《Structural Health Monitoring》2014,Vol.13,No.2)等论文。 E-mail:gliu@cqu.edu.cn

