规避姿态禁区的航天器姿态机动路径规划
缪远明 潘腾
(北京空间飞行器总体设计部, 北京 100094)
规避姿态禁区的航天器姿态机动路径规划
缪远明 潘腾
(北京空间飞行器总体设计部, 北京 100094)
对航天器姿态机动进行路径规划以规避姿态禁区,能有效保障航天器安全运行,提高在轨寿命。文章研究了多约束条件下的航天器姿态机动路径规划问题,将工程约束表达成明确的函数,提出了基于比例微分控制的编码方法,设计了一种以机动时间最短为目标的评价函数,将路径规划问题转换为最优化问题,采用粒子群优化算法进行最优解搜索,在可接受的代价范围内得到了满足约束的机动路径。仿真结果表明,该方法对于禁区规避问题是有效的。
姿态机动;禁区规避;路径规划;编码;粒子群算法
1 引言
多数情况下,航天器进行姿态机动时都要规避一些危险的指向:如不能将低温冷却望远镜或星敏感器指向太阳或者其它明亮的区域;不能将散热面长期暴露在太阳辐射下;穿越行星环或小行星带时,未经加固的表面不能指向容易受到撞击的方向等[1-2]。把这类危险的姿态指向称为姿态指向禁区,姿态机动时,寻找一条安全、便捷的路径规避指向禁区是航天器姿态机动路径规划的核心任务。
针对这类问题,卡西尼(Cassini)探测器的约束监测算法[3]和Hari B等人提出的1-cosθ型路径绕行禁区的规划方法[4]均实现了姿态运动的自主规划,并有较好的实时性,但缺点在于无法对路径进行有目标的优化。McInnes等人通过构造虚拟势函数和导航函数,使姿态沿着势函数减小的路径“自然”地落入全局势能最低点,同时实现姿态机动和障碍规避[5-6],但此方法难以考虑动力学约束且易陷入局部最优。Kim Y等人将动力学约束和几何约束都转换为与系统状态量相关的矩阵不等式,从而将路径规划问题转换成半定规划问题[7],但该方法的复杂度会随着约束增加而急剧增大。
综上分析,姿态机动路径规划应针对明确的性能指标而进行,能考虑全面的几何约束和动力学约束以及有较强的实际可操作性。本文首先描述了卫星在姿态机动过程中需要考虑的动力学约束和几何约束,其次对基于比例微分控制的编码方法和评价函数构造进行了介绍,最后通过一个仿真实例验证了本文提出的方法是有效的。
2 姿态机动问题描述
本文在刚体动力学的基础上进行姿态机动路径规划,刚体姿态动力学相关内容详见参考文献[8]。在姿态机动过程中,需要考虑的约束主要为来自卫星自身的动力学约束和来自外部环境的几何约束。
动力学约束为星上控制力矩T=[T1T2T3]T有界和卫星本体角速度ω=[ω1ω2ω3]T有界,表示为
|Ti|≤Tmax,i=1,2,3
|ωi|≤ωmax,i=1,2,3
(1)
几何约束包括“不得靠近”和“不得远离”两种。以明亮天体不得进入星上光学敏感设备视场的约束为例,设星上敏感设备指向矢量在地心赤道坐标系中定义为b,视场角为θ,卫星指向明亮天体的矢量在地心赤道坐标系中记为v,则机动过程中应满足[9]
(2)
同理,若姿态机动时要求指向b偏离目标指向v的角度不超过θ,则有
(3)
3 路径规划方法
提出了一种基于比例微分控制的编码方法,设计了以机动时间最短为目标的评价函数,将无限维的路径规划问题转换成对有限个中间节点寻优的最优化问题,采用粒子群算法对其进行求解,流程如图1所示。

图1 路径规划流程Fig.1 Flow chart of path planning
3.1 应用比例微分控制的编码方法
航天器姿态机动路径的本质是一系列有序的姿态状态的集合,对姿态机动路径进行规划就是规划每一时刻航天器所处的姿态,显然直接对无限个时间点上的姿态进行规划是不现实的。需要一种方法,仅需对有限点的姿态进行规划或仅需要确定有限个参数就能达到路径规划的目的。
本文提出了一种应用比例微分控制的编码方法,对直接欧拉机动违反几何约束的机动路径,通过若干个有序的姿态节点依次对路径进行吸引,从而达到规避约束区域的目的,如图2所示。

图2 利用中间姿态节点吸引路径规避约束区域Fig.2 Avoiding celestial constraints using the sattraction of the middle attitude node
(4)
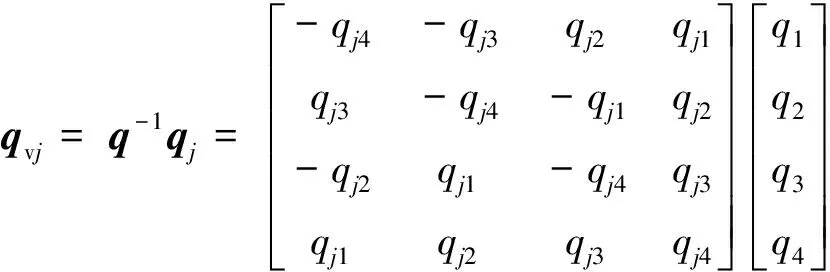
(5)
式中:q为航天器当前姿态四元数,ω为航天器当前姿态角速度。得到控制力矩后根据姿态动力学即可得到航天器姿态。
3.2 评价函数构造
将评价函数设置为越小越好型,通过寻找评价函数的最小值来得到最优路径。考虑以机动时间最短为目标进行路径规划,若路径不违反约束,则评价函数为机动时间
Jt=tf-ts
(6)
式中:Jt为机动时间评价值,tf为机动结束时间,ts为机动开始时间。
若路径违反约束,评价函数将在机动时间的基础上急剧增大:对于要保证矢量夹角大于一定值的约束
(7)
相反地,对于保证矢量夹角小于一定值的约束
(8)
式中:Jg1、Jg2为指向约束评价值,C为一个较大的常数,以划分约束区域的边界。
总评价函数为
(9)
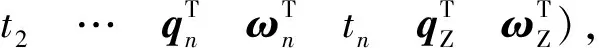
4 仿真分析
考虑以下仿真实例:在地心赤道坐标系中,卫星初始姿态四元数为q0=(0 0 0 1)T,初始角速度为ω0=(0 0 0)T,望远镜初始指向为r0=(0 0 1)T,太阳矢量方向rs=(0.75 -0.17 0.64),月球矢量方向rm=(0.97 0.21 -0.08),任务要求将望远镜指向调整为rt=(0.71 0 -0.71)T,并在机动过程中望远镜与太阳和月球矢量的夹角均不得小于θmin=15°,卫星转动惯量为I=diag[2000 2000 2000]kg·m2,飞轮最大输出力矩为Tmax=0.12 N·m。机动终止条件为指向误差小于0.1°,角速度误差小于0.01(°)/s。规划结果如图3~8所示。

图3 姿态机动路径Fig.3 Attitude slew path

图4 四元数曲线Fig.4 Quaternion curve

图5 角速度曲线Fig.5 Angle velocity curve

图6 控制力矩变化曲线Fig.6 Control torque curve
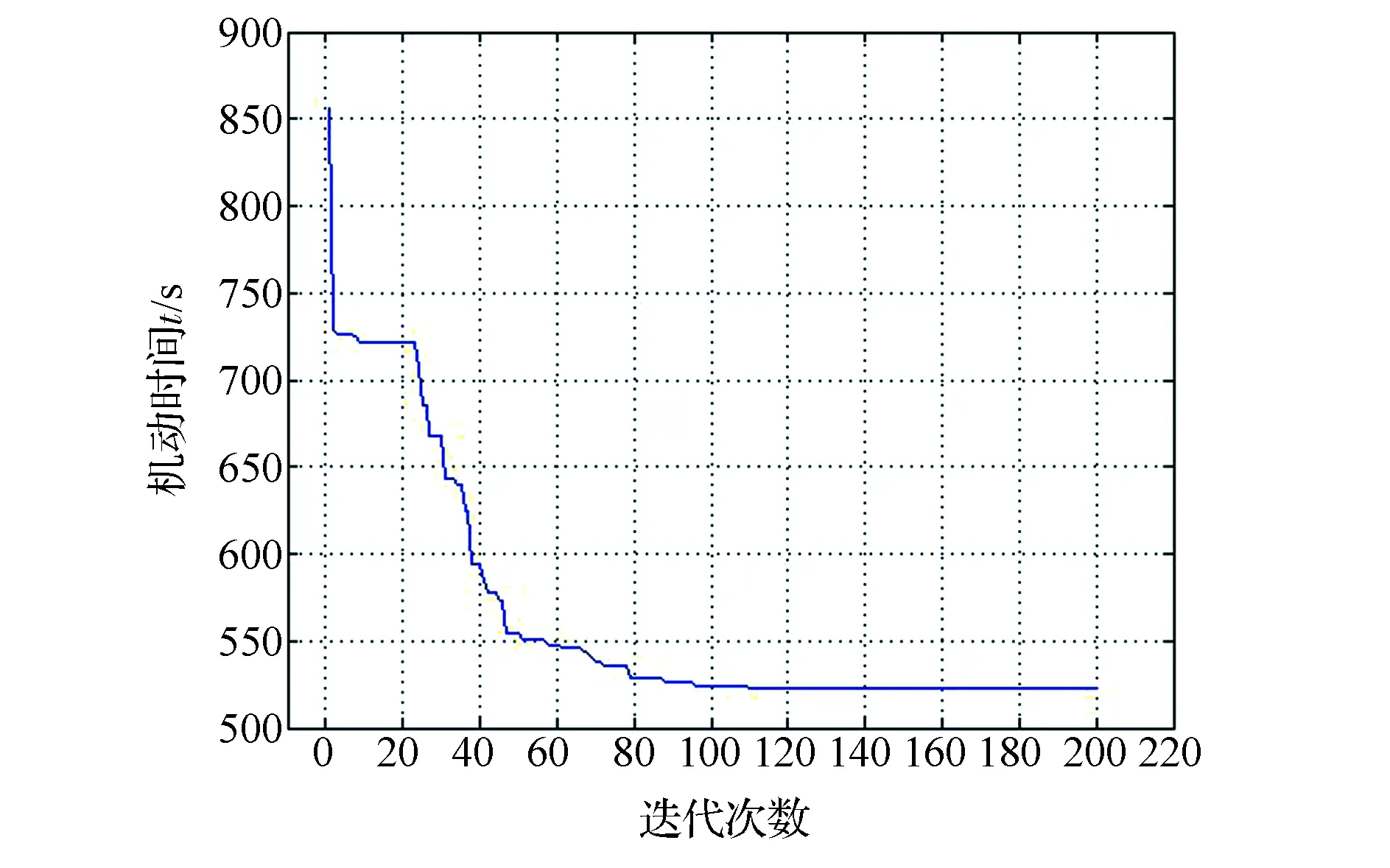
图7 评价函数优化过程Fig.7 Optimization process of time cost of slew

图8 迭代优化过程中的机动路径Fig.8 Slew path in the process of optimization
机动过程总共耗时523 s。图3中“机动路径”为机动过程中,望远镜指向矢量r在以航天器质心为中心的惯性天球表面的投影;“指向禁区”为以航天器质心为顶点,以约束天体矢量轴为旋转轴,半锥角为θmin的圆锥与单位惯性天球表面的交线。可以看出,在整个机动过程中,太阳、月球与望远镜矢量的夹角始终大于θmin,即在整个机动过程中满足几何约束。
姿态四元数、姿态角速度和控制力矩如图4~6所示,由图中可以看出,机动过程中控制力矩未超过0.12N·m,满足动力学约束。同时,由于在规划过程中同时对控制参数KP,KD进行了优化,航天器在机动末期可以较快地静止,不产生振荡。
图7表达的是路径的评价函数随优化的进行逐渐减小的过程,图8展示了优化过程中的路径。可以形象地看出,第3章中提出的路径规划方法对路径的优化是有效的。
5 结论
本文提出的姿态机动路径规划方法,可以解决存在姿态禁区的姿态机动路径规划问题,其具有如下优点:
(1)能针对具体的指标,如机动时间进行路径规划,并且能全面考虑各种几何约束和动力学约束。
(2)相比势函数法和半定规划法等,该方法中约束形式简单,无需复杂变形,易于添加新的约束。
(3)在进行路径规划的同时,也对控制参数进行优化,使得卫星姿态角速度整体呈现匀加或匀减的趋势,并且在机动末期能够较快地静止,避免了因为控制参数选取不当导致的姿态震荡。
References)
[1]Frazzoli E, Dahleh M A, Feron E, et al. A randomized attitude slew planning algorithm for autonomous spacecraft[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.:AIAA,2001
[2]Richard P Kornfeld. On-board autonomous attitude maneuver planning for planetary spacecraft using genetic algorithms[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington D.C.:AIAA,2003
[3]Singh G, Macala G, Edward C Wong, et al. A constraint monitor algorithm for the Cassini spacecraft[C]//Proceeding of AIAA Guidance, Navigation and Control Conference. Washington D.C.:AIAA, 1997:272-282
[4]Hablani H B. Attitude commands avoiding celestial objects and maintaining communication with ground station[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(6):759-767
[5]McInnes C R. Large angle slew maneuvers with autonomous sun vector avoidance[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(4):875-877
[6]Avanzini G, Radice G, Ali I. Potential approach for constrained autonomous manoeuvres of a spacecraft equipped with a cluster of control moment gyroscopes[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2009, 223(3):285-296
[7]Kim Y, Mesbahi M. Quadratically constrained attitude control via semidefinite programming[J]. Automatic Control, IEEE Transactions On, 2004, 49(5):731-735
[8]章仁为. 卫星轨道姿态动力学与控制[M]. 北京:北京航空航天大学出版社, 1998
Zhang Renwei. Satellite orbit and attitude dynamics and control[M].Beijing:Beihang University Press, 1998 (in Chinese)
[9]程小军, 崔祜涛, 徐瑞, 等. 几何约束下的航天器姿态机动控制[J]. 控制与决策, 2012, 27(5):724-730
Cheng Xiaojun, Cui Hutao, Xu Rui, et al. Attitude maneuver control of spacecraft under geometric constraints[J]. Control and Decision, 2012,27(5):724-730(in Chinese)
[10]纪震, 廖惠连, 吴青华. 粒子群算法及应用[M]. 北京:科学出版社, 2009
Ji Zhen, Liao Huilian, Wu Qinghua.Particle swarm optimization algorithm and its application[M].Beijing: Science Press, 2009 (in Chinese)
(编辑:李多)
Path Planning Method for Spacecraft Attitude Slew to Avoid Forbidden Celestial
MIAO Yuanming PAN Teng
(Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)
The path planning for attitude slew of a spacecraft to make forbidden celestial avoidance could enhance the safety and increase the durability of an on-orbit spacecraft. The path planning for the attitude slew under a number of celestial and dynamic constraints is studied in this paper. Engineering constraints are described as simple functions. A way of encoding based on proportional-differential control is presented. An evaluationt function which aims at the shortest time for slew is designed. Therefore, the path planning is transformed into an optimization process. A feasible path can be found at an acceptable cost by using a particle swarm optimization algorithm. The simulation result shows the validity of the method in the use of forbidden celestial avoidance.
attitude slew; forbidden celestial avoidance; path planning; encoding; particle swarm optimization algorithm
2015-03-18;
2015-06-16
国家重大航天工程
缪远明,男,硕士研究生,研究方向为航天器总体设计。Email:yuanming_miao@163.com。
V442.8
A
10.3969/j.issn.1673-8748.2015.04.006

