双股线几何强力模型的建立及其影响因素
黄 伟,汪 军,2
(1.东华大学纺织学院,上海 201620;2.东华大学纺织面料技术教育部重点实验室,上海 201620)
纱线结构的研究开始于20世纪30年代,落后于纤维和织物,到50年代才有了较为明显的进展[1]。在分析纱线结构时,由于其复杂性和多重性,所以往往需要从纤维排列的理想状态入手,建立纱线理想的几何模型[2]。其中一些研究者从理论角度上的研究既系统又详尽。理论成果包括Platt[3-4]提出了纱线张力应变与纤维张力应变的关系;Hearle[5]考虑拉伸力、横向力与外侧收缩的作用影响,推导了张压应力在纱线不同位置上的关系表达;后来Nachane[6]从单纱段的短片段受力分析入手认为,单纱中的张力分量和剪切分量共同贡献了纱线的伸长,推导了能较好符合实验趋势的双股线张力拉伸方程;此后他通过进一步研究推导出理想加捻复合长丝纱关于载荷、伸长和比模量的公式[7],比前人的研究在公式预测上与实验数据更加接近。本文研究运用该方法建立了关于双股线结构的理想几何模型,并在此基础上研究股线捻度和单纱之间的作用力与其强力的关系。
1 股线强力增强效应
本文研究的对象股线作为其在结构上的体现,是由2根及以上的单纱(长丝或短纤纱)并合加捻而成,其中双股线是最简单的股线种类,如图1所示(θ为捻回角,rf为单纱半径)。经多项实验和生产数据所得,加捻是股线增强效应的主要因素[8],这种股线强力超过组成单纱强力之和的现象称为股线增强效应。对于这种现象的本质研究,国内外也有许多研究成果予以论证。通过实验数据与理论上对股线强力的增强效应影响因素分析得到,加捻能使纤维间的抱合和交互作用增强,从而使断裂不同时性降低,在低捻和长丝纱中尤为明显。纤维间作用力的增强直接体现为纤维间摩擦力的增加,从而增强整体纱线的强力,但当捻度增加到一定程度后,过大的单纱倾斜角使纤维轴向分力减小,影响其强力的有效利用,因此在捻度和横向压力的双重影响下,纱线的强力在随捻度增加的过程中存在极大值,此时纱线的捻系数被称为临界捻系数,而这种现象在股线加捻的过程中同样存在。

图1 双股线几何模型Fig.1 Geometric model of ply yarn.(a)Longitudinal section;(b)Cross section
但是关于股线强力的研究目前大都停留在借助实验来探寻数据变量之间的规律,缺乏定量分析。从常见的纱线参数入手,建立了关于双股线的几何模型,分析了单纱短片段在拉伸载荷下的拉伸行为;然后将股线捻度与单纱之间的摩擦力作为影响股线强力的主要因素,最终以较少的变量参数推导了股线的强力表达式,并证明了股线具有类似于单纱加捻时临界捻系数的存在。
2 模型建立及求解
考虑到长丝股线的强力组成主要由其单纱性能及单纱之间因加捻弯曲而产生的抱合力决定,故分别研究单纱性能对股线拉伸行为的影响与拉伸时抱合力引起的单纱之间摩擦力对强力贡献的情况,方法上遵循经典力学上物理变量的关系。
2.1 条件假设
双股长丝纱拉伸强力对股线与单纱捻比变化不显著,故可忽略单纱捻度的存在;且股线的拉伸行为类似于单纱[9]。建立理想模型如图1所示,并作如下假设:1)单纱为1根连续长丝纱,截面圆形,沿长度方向均匀,且2根单纱性质相同;2)单纱路径为等螺旋线,离股线轴线距离不变,倾斜角不变,即捻度沿轴线方向不变;3)考虑为低捻环境下,忽略因加捻程度不同而引起的单纱预伸长的影响,捻回角与单纱线密度随加捻过程及拉伸过程中的变化;4)在单纱拉伸伸长过程中,纱线应力与应变的关系遵循胡克定律,即拉伸模量为定值;5)因加捻而使单纱之间产生的抱合力在单纱长度方向上处处相等。
2.2 模型构成
对股线的拉伸强力和增强效应影响因素分析之后可得,股线总强力由2部分组成:一是假设为遵循胡克定律而线性增加的拉伸力;二是在拉伸时因加捻产生的单纱间相互作用力,在此体现为单纱之间摩擦阻力,体现在公式关系即为:

式中:Tt为股线总强力;Ty为股线拉伸力;fy为摩擦阻力。以下分别推导等式右边的变量表达式。
2.3 模型求解
1)根据连续介质力学理论结合假设条件,拉伸力的基本公式为:

式中:Ay为纱线横截面面积;εy为断裂应变;Ey为股线拉伸模量。
据图1所示,rf为单纱半径,则双股线截面情况为

Ey是由单纱模量和捻回角确定的,如图2所示。假设纱线承受载荷2T的作用,每根长丝沿纱轴方向承受T的载荷,分解而得的拉伸分力Tcosθ和剪切分力Tsinθ共同导致了纱线的伸长。则在一个螺线捻度内的单纱长度Lf贡献给沿纱轴上的伸长为

又因为在一个捻度内单纱长度Lf与股线长度Ly存在Ly=Lfcosθ的关系,则股线应变△Ly/Lf为

则据式(2),Ty=2T,拉伸模量为
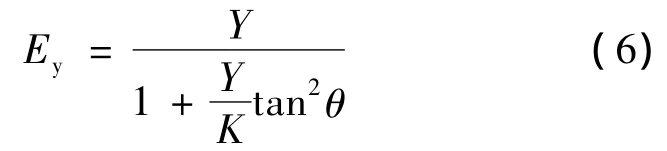
式中:Y为单纱弹性模量;K为单纱剪切模量;θ为股线捻回角。

图2 短片段上力的分解Fig.2 Directions of forces acting on an element in Nachane's study
2)复合纱线中2组成分之间摩擦阻力的计算方法[10]如下:

式中:μ为摩擦因数;N为径向压力;α为抱合系数;S为接触面积。
径向压力即单纱因加捻弯曲产生的向心压力,关系如图3所示[11],则可得到以下关系式:

又因为当 φ 很小时,sinφ/2 ≈ φ/2;φ=l/ρ,ρ =r/sin2θ,则

图3 单纱对纱线向心压力的分解Fig.3 Centripetal force decomposition

式中,t为所受张力,φ为包围角,r为离轴线距离,β为横截面上l转过的角度。
在本文研究中,t=Ttcosθ/2,β=π,则

将各个关系代入式(1),则模型的最终表达式为:

3 分析与讨论
根据式(13)可看出,等式右边具体参数为单纱半径rf、股线捻回角 θ、拉伸应变 εy、抱合系数 α、单纱拉伸模量Y、单纱剪切模量K。关于参数对最终股线总强力的影响分析如下。
3.1 拉伸与剪切模量的影响
据式(13)所知,单纱模量对股线总强力的影响是体现在股线拉伸模量Ey上的,而Ey/Y为股线与单纱的模量比,体现单纱双股捻合后整体模量的变化,所以比较不同拉伸模量Y和剪切模量K对Ey/Y的影响即可,4种不同材料的模量属性见表1。在式(6)中,捻回角θ取π/12,经由MatLab计算并绘图结果如图4所示。从图中可看出,单纱加捻成股线结构后,整体拉伸模量会有一定比例的减小。结果显示,在捻回角相同的情况下,不同材料组成的单纱拉伸模量与剪切模量的比值越大,其总体模量减小的比例越大,则对应合股的纱线的抗拉能力则越差。

表1 材料属性Tab.1 Material properties

图4 股线单纱模量之比与材料的关系Fig.4 Relationship between material type and modulus ratio of ply yarn and single yarn
3.2 细密度的影响
纱线的强力一般与其细密度呈正相关趋势,即细密度越大,截面范围内能承受的纤维根数越多,则纱线强力越高。而化纤单纱支数与其直径的表达式[13]如下:

式中,df为单纱直径,δ为单纱密度,Ne为英制支数。由式(13)可知,股线强力随单纱直径的平方呈线性增加关系,结合上式可得出,纱线的强力与单纱的支数呈简单的反比关系,符合一般认识。
3.3 抱合系数的影响
抱合系数用来反映纤维之间抱合程度的参数,据式(5)可计算单纱之间的摩擦力。在纺织纱线领域,一般系数取值为0.4~0.6[10]。本文研究考虑了2根单纱界面摩擦力的因素,即在拉伸过程中界面存在相对滑动的趋势(未发生相互滑移的情况下)。图5示出不同抱合系数对股线总强力的影响情况(材料为 PA6,直径为0.2591 mm,由式(14)确定,应变取0.25,捻回角为π/12)。

图5 抱合系数与总强力的关系Fig.5 Relationship between cohesion factor and total strength
经由MatLab计算并绘图结果显示,抱合系数对股线强力的影响是正相关的,即抱合系数α越大,单纱之间的摩擦力越大,最终体现在对总强力的贡献越大,所占比例较拉伸部分影响较小,最大情况下不超过总强力的10%。
3.4 捻回角的影响
加捻是股线增强效应最主要的因素,而捻回角的大小是描述加捻程度的客观指标。以双股线材料PA6,直径为0.2591 mm,应变0.25为例,描述股线强力、拉伸力和摩擦力随捻回角增加的变化情况,经由MatLab计算并绘图,结果如图6所示。

图6 总强力、拉伸力和摩擦力随捻回角的变化情况Fig.6 Total strength,tensile strength and friction changes along with ply yarn's twist angle
结果表明:拉伸力随着捻回角的增大,股线总体拉伸模量不断减小,而摩擦力则从0开始逐渐增大,在31°附近达到最大,随后逐渐减小;而当捻回角在12°附近时,股线的强力出现极大值,这类似于单纱加捻时会出现临界捻系数,此现象在此也得到了证明。最终对捻度增强效应的解释为:若只考虑轴向力的影响,捻度的改变对强力无增强作用;若将由于加捻作用引起的单纱间摩擦力考虑进来,则在加捻到一定程度之前,总强力会有一定的增强效果,并可从公式关系上定量确定双股线的临界捻系数大小。
3.5 单纱变化的影响
3.1 小节只讨论了单纱的变化对股线拉伸模量的影响关系,若将这种关系放宽到影响整体股线强力时,类似于3.4中只讨论一种材料,结合式(6)、(14),及表1中的单纱材料属性,经由MatLab计算并绘图给出了当抱合系数为0.5时,同一应变下(0.25)其强力随捻回角的变化情况,如图7所示。

图7 单纱变化对总强力的影响Fig.7 Effect of single yarn types on total strength
结果显示,4种不同材料组成的股线总强力都呈现出如图6所示的趋势,即随着加捻程度的加大,单纱之间抱合力的增加趋势大于因单纱取向分力减小的趋势,其总体强力会呈现出增大的趋势,但随着取向角度不断增大,摩擦力也呈现出如图6的衰减趋势,而取向分力下降趋势更加显著,其结果导致总强力出现极大值后的不断减小。
通过上述研究发现,单纱的性质和股线的结构共同决定着股线的性质,本文研究采用较少的可调参数推导了关于双股线强力的数学模型,能用来量化解释股线中的单纱和股线结构对其总强力的影响情况,参数包括单纱半径rf、股线捻回角θ、拉伸应变εy、抱合系数α、单纱拉伸模量Y、单纱剪切模量K,这些参数与整体股线的强力有着密切的关系。而最终的模型也能够用来分析已生产的成品股线性能,可用来描绘单纱的变化对股线拉伸行为的影响,通过单纱模量及其他参数可用来预测加捻过程中股线达到最大强力时的捻度水平,同时可量化分析单纱的变化对股线强力的影响情况。
4 结论与展望
本文研究从双股线模型的几何配置出发,认为股线捻度的变化及单纱之间作用力共同决定了股线的强力,经研究与推导发现如下关系及结论:1)在理想纱线模型的基础上,建立了双股线理想模型的几何配置,并给出模型的假设条件;2)分析了单纱短片段在拉伸载荷下轴向和径向的力学状态对拉伸行为的作用后,得出其拉伸模量上与单纱模量的关系式;3)将单纱之间的抱合力考虑为组成股线强力的一部分,推导了在单纱无滑移情况下股线强力的表达式,定量分析讨论了单纱性能参数及加捻程度对股线最大强力的影响情况;4)最终模型能够用来分析成品股线性能;描绘单纱变化对股线拉伸行为和产品强力的影响;通过较少的参数就可用来预测加捻过程中股线达到最大强力时的捻度水平。
将来进一步的研究将考虑初始预应力及加捻引起的捻缩现象对单纱及最终强力的影响;将单纱具体化为束纤维、加捻长丝纱或短纤纱;在实验验证与修正方面的工作,也会同期进行。
[1] CORBMAN B P.Textile,Fiber to Fabric[M].6nd ed.New York:McGraw-Hill Book Co,1983:Chapter 3.
[2] RIDDLE E R.Preliminary considerations in a plan of work to develop fiber-yarn models [C]//Proc Engineered fiber selection mini conference.Raleigh:Raleigh cotton incorporated,1988:161.
[3] PLATT M M.Mechanics of elastic performance of textile materials:part III:some aspects of stress analysis of textile structures-continuous-filament yarns[J].Text Res J,1950,20:1-15.
[4] PLATT M M.Mechanics of elastic performance of textile materials:part IV:some aspects of stress analysis of textile structures-staple fiber yarns[J].Text Res J,1950,20:51.
[5] HEARLE JWS, GROSBERGP, BACKERS.Structural Mechanics of Fibers, Yarns and Fabrics[M].New York:John Wiley & Son Inc,1969:175-207.
[6] NACHANE R P,KRISHNA IYER K R.Yarn tension as a function of extension:a new approach[J].Text Res J,1987,57:279 -282.
[7] NACHANE R P. Yarntensionasafunctionof extension:anew approach-application to an ideal twisted multifilament yarn[J].Text Res J,1990,60:128-136.
[8] 聂毓洪,袁斌钰.股线中单纱几何配置和股线强力的力学分析[J].纺织学报,2006,27(7):19-22.NIE Yuhong,YUAN Binjue.Geometric disposition of the single yarns and mechanical analysis of strength in ply yarn[J].Journal of Textile Research,2006,27(7):19-22.
[9] PALANISWAMY N K,PEER Mohamond A.Effect of single yarn twist and ply to single yarn twist ratio on strength and elongation of ply yarns[J].Journal of Applied Polymer Science.2008,98(5):2245-2252.
[10] 安降龙,郁崇文.赛络纺复合纱线结构及其拉伸力学模型[J].东华大学学报:自然科学版,2010,36(1):15-20,25.AN Xianglong,YU Chongwen.Mechanical model of sirospun composite yarn[J]. Journal of Donghua University:Natural Science Edition,2010,36(1):15-20,25.
[11] 任家智.纺纱原理[M].北京:中国纺织出版社,2002:133.REN Jiazhi.Principles of Spinning[M].Beijing:China Textile& Apparel Press,2002:133.

