正弦波电动势永磁无刷直流电动机稳态特性计算

赵 鹏，贾 晶，王瑞琪，于 芃，孙树敏，毛庆波

(国网山东省电力公司电力科学研究院，济南250002)

0 引 言

对于采用电子换相的永磁无刷直流电动机，由于换相是在相绕组之间进行，其换相电感远大于有刷直流电动机的换相电感，传统忽略绕组电感的电路模型在预测电机性能时存在一定的误差，对高速永磁无刷直流电动机，绕组电感及其换相过程对电机的性能影响更加明显。根据气隙磁场波形和绕组形式的不同，永磁无刷直流电动机一般是正弦波反电势或梯形波反电势，常将永磁无刷直流电动机视为梯形波反电势。但在许多应用领域，即使是方波气隙磁场，但由于采用分布绕组，也会形成正弦波反电势。

目前一些学者研究了计及绕组电感的方波永磁无刷直流电动机电流的计算，但对正弦波永磁无刷直流电动机、并考虑电感和换相过程的研究不多。本文针对正弦波电动势永磁无刷直流电动机的稳态特性计算，详细分析了两相导通星形三相六状态的运行模式，基于相绕组端电压方程，建立了相电流解析计算公式。根据三相绕组的对称性，将整个计算周期缩短为1/6 周期进行求解，即对电机运行一个周期六个状态中的一个状态进行求解，解决了解析计算所需的初始条件求解问题，实现了正弦波电动势永磁无刷直流电动机的稳态性能仿真。

1 电机本体的结构和电路模型

图1 为典型两相导通星形三相六状态永磁无刷直流电动机及其控制系统等路图。

图1 永磁无刷直流电动机及其控制系统等效电路图

为了简化正弦波永磁无刷直流电动机稳态特性的计算，做如下假设:

(1)功率半导体器件均为理想开关元件，忽略管压降。

(2)三相绕组空间上对称分布，各相绕组的等效电路参数对应相等，忽略磁路饱和的影响。

(3)转子永磁体产生的气隙磁场按正弦波分布，反电势为标准的正弦波。

对于图1 的电机模型，永磁无刷直流电动机三相绕组的电压平衡方程组:

式中:R 为定子绕组每相电阻;Lσ为定子绕组每相电感;un为中位点对地电压;ua，ub，ub为三相绕组端电压;ia，ib，ic为三相绕组相电流;ea，eb，ec为三相绕组反电势。

正弦波永磁无刷直流电动机三相绕组的反电势:

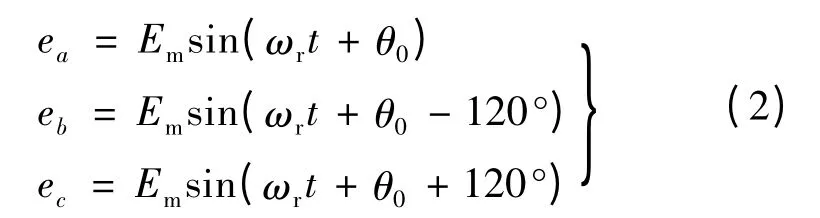
式中:ωr为转子的电角速度;θ0为转子角位移的初始值;Em为反电势幅值。

2 正弦波电动势永磁无刷直流电动机的稳态特性计算

对于两相导通三相六状态正弦波永磁无刷直流电动机，逆变器为120°导通方式，由于绕组电感的影响，功率开关元件存在换流重叠过程，电机的每种运行状态将包含:①只有两个功率开关元件导通的模式;②同时有两只功率开关管和一只续流二极管导通的换相模式。但每种状态下两种导通模式总的延续时间仍为1/3 周期，一个完整运行周期包含6种状态。表1 给出了六种状态下开关元件、二极管的导通情况以及对应的导通时间。

考虑到电机运行模式的周期性和三相绕组电流的对称性，可将表1 中状态1 作为计算区间，即仅以AB 导通到AC 导通的换相模式和AC 导通模式为例分析正弦波永磁无刷直流电动机的运行模式，它开始于晶体管VT6 关断时刻，终止于VT3 导通时刻，如图2 所示。

为了在选定的分析区间内明确划分出换相模式和导通模式的持续时间，需要求解换相时间tc和初始电流I0。最后，根据三相绕组电流的对称性，其余5 种状态可由状态1 的计算结果获得。图3 为120°导通模式一个周期内的A 相电流。

表1 永磁无刷直流电动机的导通模式

2.1 换相模式

以AB 导通到AC 导通的换相模式的起始时间为初始时刻。此时，转子位于θ0=π/2 处［5］，A 相和B 相的初始电流ia(0 +)=ib(0 +)=I0，换相时间为tc。根据等效电路图2(b)，回路电流方程:

根据式(3)求得换相模式三相电流表达式:

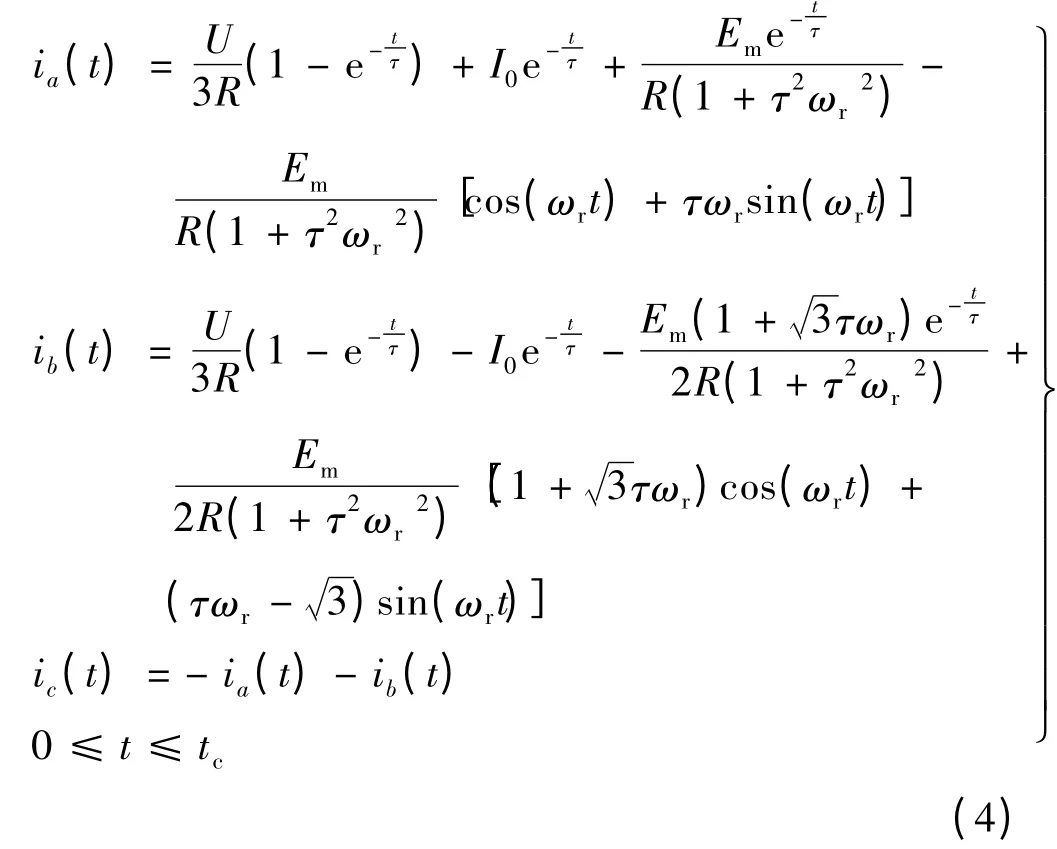
式中:τ=Lσ/R，τ 为电磁时间常数。

2.2 导通模式

当B 相电流衰减为零，即ib(tc)=0，换相模式结束。电机进入AC 导通模式，导通时间为tc≤t≤t2。根据图2(c)，回路电流方程:

根据式(5)求得换相模式三相电流表达式:

2.3 计算换相时间和初始电流

当逆变器运行在120°导通模式下，AB 导通到AC 导通换相模式结束时，B 相电流变为零，即:

当电机运行在AC 导通到BC 导通的换相模式时，A 相的电流变化了1/6 周期，根据三相变量60°对称关系［6］，此刻A 相的初始电流也为I0，即:

式中:

合并式(8)和式(9)，得到只包含未知量tc的方程:

由于式(10)是包含未知量tc的超越方程，无法求得解析值，可采用Newton- Raphson 方法迭代求解。

求得换相时间tc后，通过式(8)求得初始电流I0，并通过式(4)和(6)求得状态1 的A 相、B 相和C相绕组电流。根据电机运行模式的周期性和三相电流的对称性，求得表1 中其余5 个状态的A 相电流。

由图3 可得A 相绕组处于导通模式期间的平均电流:

正弦波永磁无刷直流电动机的电磁转矩可由电磁功率和机械角速度值求出:

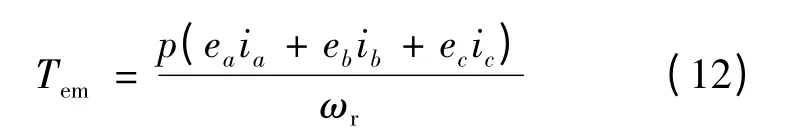
式中:p 为电机的极对数。

由图3 和式(12)可得电机的平均电磁转矩:

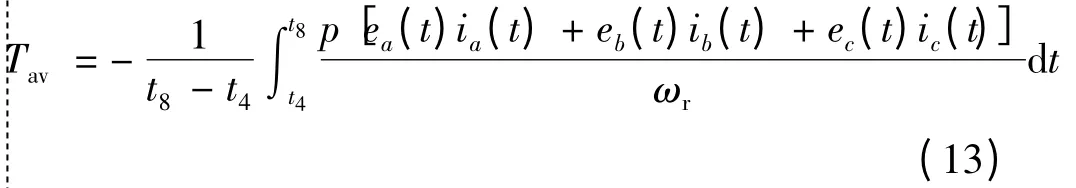
3 计算实例与仿真波形

样机是外转子方波永磁无刷直流电动机，额定电压U =48 V，极对数p =23，每相绕组电阻R =0.312 Ω，每相绕组电感Lσ=0.512 mH，电机转速n=350 r/min，对应反电势幅值Em=22.67 V。

图4 为通过有限元分析获得的电机气隙磁密波形及实测反电势波形。从图4 可见，尽管电机的气隙磁密为梯形波，但绕组反电势波也有正弦化的趋势。

为获得正弦波气隙磁场，对该方波永磁无刷直流电动机的磁钢进行不均匀气隙改造，经有限元分析获得正弦气隙磁密与反电势波形如图5 所示，正弦气隙磁密幅值和反电势幅值与原来方波样机的幅值基本相同。

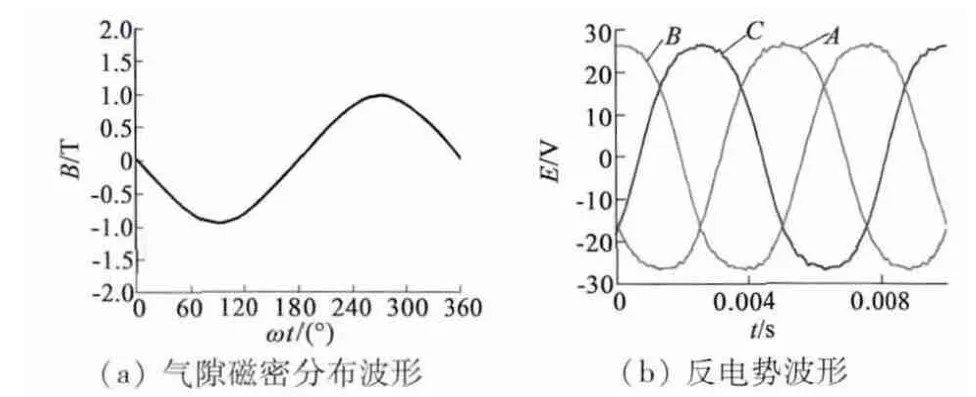
图5 正弦波永磁无刷直流电动机气隙磁密和反电势

根据式(10)求得换相时间tc=2.205 2 ×10-4s，代入式(8)可得初始电流I0=11.712 5 A。由式(4)、式(6)和式(12)求得正弦波永磁无刷直流电动机三相电流波形和转矩波形，如图6 所示。

采用计及电感的电路模型，计算转速n =350 r/min 下的正弦永磁无刷直流电动机的基本性能参数，如表2 所示。

图6 三相电流ia，ib，ic 和转矩Tem波形

表2 电机基本参数的仿真计算值

当假定绕组电感为零时(此时不存在换流模式)，按本文推导的计及绕组电感电路模型公式，计算的相电流波形如图7 虚线所示。

图7 A 相电流有电感和无电感的计算波形

由式(11)和式(13)推导出忽略电感时两相导通星形三相六状态正弦波永磁无刷直流电动机相绕组平均电流Iav、平均电磁转矩Tav以及反电势系数KT，如表3 所示。

表3 Lσ =0 时Iav，Tav和KT 的计算公式

对比采用传统忽略绕组电感的稳态电路模型计算的平均电枢电流［7］与本文采用计及绕组电感的电路模型且假定绕组电感为零时计算的平均电枢电流，两者的计算值完全吻合，如表4 所示。因此传统忽略电感的相电流计算公式可视为本文公式的特例。从表4 和图7 可以看出，电感对正弦波永磁无刷直流电动机平均电枢电流计算值影响是比较大的，两者相差一倍以上。分析正弦波永磁无刷直流电动机应该考虑绕组电感对电机性能影响。

表4 两种电路模型绕组电流计算比较

4 结 语

本文基于两相导通星形三相六状态的正弦波永磁无刷直流电动机的相绕组端电压平衡方程，推导了其相绕组电流的解析表达式，仿真计算了计及绕组电感的正弦波永磁永磁无刷直流电动机的稳态特性。比较研究了正弦波永磁无刷直流电动机计及电感电路模型与传统忽略电感电路模型的性能参数计算差异，研究表明绕组电感对正弦波永磁无刷直流电动机的运行性能影响较大，不能忽略。

［1］ NEHL T W，DEMERDASH N A.Impact of winding inductance and other parameters on the design and performance of brushless DC motor［J］.IEEE Trans. on Power App. and Syst.，1985，PAS104:2206 -2213.

［2］ ZHU Z Q.Analytical prediction of dynamic performance characteristics of brushless drive［J］.Electrical Machine and Power System，1992，20(6):661 -678.

［3］ 李鲲鹏，胡虔生，黄允凯.计及绕组电感的永磁无刷直流电动机电路模型及其分析［J］.中国电机工程学报，2004，24(1):76 -80.

［4］ 余莉，刘合祥.永磁无刷直流电机电路计算模型及其换相分析［J］.微电机，2010，43(10):6 -10.

［5］ 葛新，韩光鲜，王宗培.无刷直流电动机的实用仿真模型［J］.微电机，2004，37(2):7 -8.

［6］ 贺益康，严岚. 永磁无刷直流电机稳态特性的状态空间分析［J］.电工技术学报，2002，17(1):17 -22.

［7］ 叶金虎.现代无刷直流永磁电动机的原理和设计［M］. 北京:科学出版社，2007.